|
Modelos de Regressão Não LinearFundamentos e Aplicações em R |
Medidas de diagnóstico
1 Teste da falta de ajuste
#-----------------------------------------------------------------------
# Definições da sessão.
library(lattice)
library(latticeExtra)
library(rpanel)
# library(proto)
source("https://raw.githubusercontent.com/walmes/wzRfun/master/R/as.lm.R")
source("https://raw.githubusercontent.com/walmes/wzRfun/master/R/R2nls.R")
# source("../funções/R2.R")
llayer <- latticeExtra::layer#-----------------------------------------------------------------------
# Ajustar modelo para os dados de ganho de peso de peru em função de dieta.
data(turk0, package = "alr4")
str(turk0)## 'data.frame': 35 obs. of 2 variables:
## $ A : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Gain: int 644 631 661 624 633 610 615 605 608 599 ...p0 <- xyplot(Gain ~ A,
data = turk0,
col = 1,
xlab = "Metionina (% da dieta)",
ylab = "Ganho de peso (g)")
p0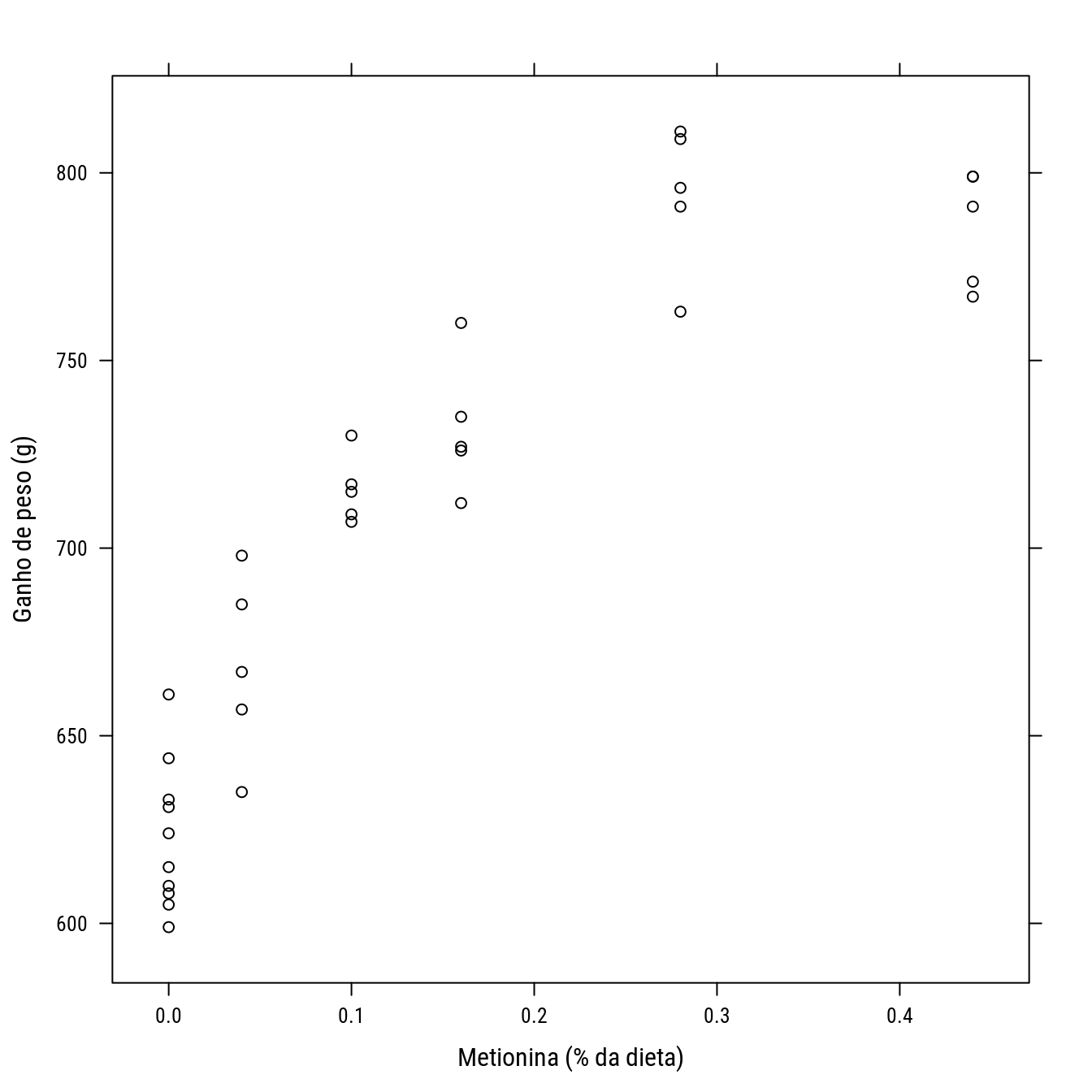
Modelo considerado pelo Weisberg (livro Applied Regression): \[ f(x) = f_0 + f_1 \cdot (1 - exp(-k \cdot x)) \]
- \(f_0\): valor da função com \(x = 0\) (intercepto).
- \(f_1\): \(\lim_{x \to \infty} f(x) = f_1 + f_0\), \(f_1\) é o ganho máximo conseguido por incremento de \(x\).
- \(k\): constante relacionada à taxa de incremento.
#-----------------------------------------------------------------------
# Valores iniciais investigados de forma interativa.
start <- list()
expon <- function(panel) {
plot(Gain ~ A,
data = turk0,
xlab = "Metionina (% da dieta)",
ylab = "Gano de peso (g)")
with(panel,
curve(f0 + f1 * (1 - exp(-k * x)),
add = TRUE,
col = 2))
start <<- with(panel, list(f0 = f0, f1 = f1, k = k))
panel
}
panel <- rp.control()
rp.slider(panel, f0, 500, 700, initval = 600, showvalue = TRUE,
action = expon)
rp.slider(panel, f1, 100, 400, initval = 200, showvalue = TRUE,
action = expon)
rp.slider(panel, k, 0, 15, initval = 1, showvalue = TRUE, action = expon)
rp.do(panel, action = expon)
start#-----------------------------------------------------------------------
# Ajustando o modelo aos dados.
# Ajuste do modelo aos dados.
start <- list(f0 = 620, f1 = 160, k = 9)
n0 <- nls(Gain ~ f0 + f1 * (1 - exp(-k * A)),
data = turk0,
start = start)
summary(n0)##
## Formula: Gain ~ f0 + f1 * (1 - exp(-k * A))
##
## Parameters:
## Estimate Std. Error t value Pr(>|t|)
## f0 622.958 5.901 105.57 < 2e-16 ***
## f1 178.252 11.636 15.32 2.74e-16 ***
## k 7.122 1.205 5.91 1.41e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 19.66 on 32 degrees of freedom
##
## Number of iterations to convergence: 5
## Achieved convergence tolerance: 3.853e-06# Verifica o ajuste obtido.
plot(Gain ~ A,
data = turk0,
xlab = "Metionina (% da dieta)",
ylab = "Gano de peso (g)")
with(as.list(coef(n0)),
curve(f0 + f1 * (1 - exp(-k * x)),
add = TRUE,
col = 2, lwd = 3))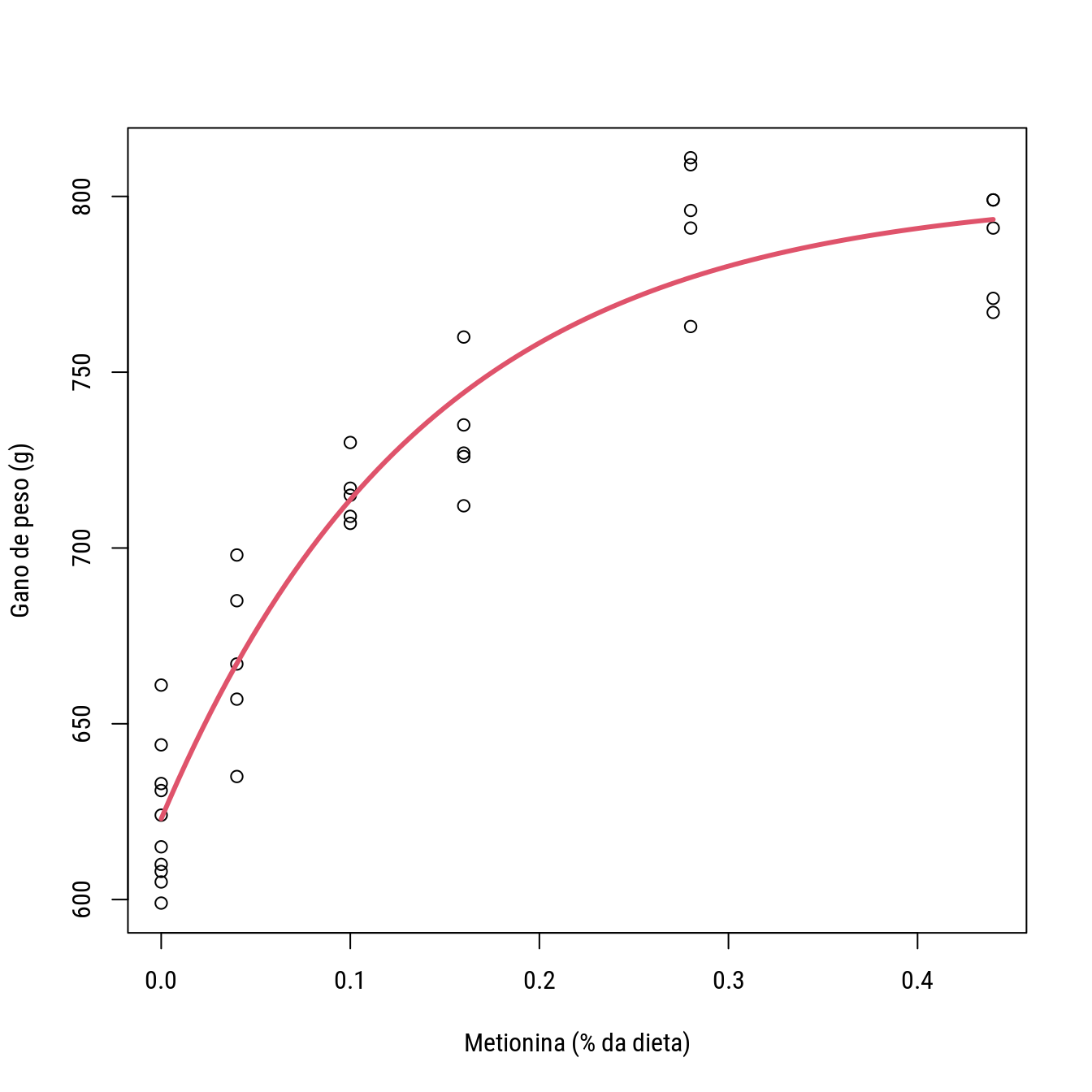
Em situações onde existem repetições dos níveis de \(x\) é possível testar a adequação do modelo. A palavra adequação foi destacada porque na realidade o modelo não linear será comparado com outro modelo que é o modelo de médias, pois assume que \(x\) é um fator qualitativo. Esse modelo é o maior modelo, considerando a especificação para o parâmetro de média, que pode ser proposto para esses dados. O número de parâmetros é o número de níveis de \(x\). O teste da falta de ajuste consiste em verificar se o modelo não linear é tão bom quanto o modelo de médias, que seria o modelo com melhor ajuste possível porém sem interpretação em termos de função e sem permitir predição de valores.
#-----------------------------------------------------------------------
# Ajusta o modelo de média de caselas.
# Modelo de médias usando o fator como qualitativo.
m0 <- lm(Gain ~ factor(A), data = turk0)
# Teste da falta de ajuste.
anova(n0, m0)
p0 +
llayer(with(as.list(coef(n0)),
panel.curve(f0 + f1 * (1 - exp(-k * x)),
add = TRUE, col = 2))) +
llayer(panel.points(x = turk0$A, y = fitted(m0),
cex = 2, pch = 4, col = "magenta"))NOTA: não necessariamente o modelo não linear tem que passar no teste da falta de ajuste para ser útil. O ideal é que passe. Se não passar, o curso de ação é buscar por um modelo mais compatível com os dados.
2 Análise dos resíduos
Complementar ao teste da LOF deve-se fazer a análise dos resíduos. O ideal se tivessemos os 4 gráficos disponíveis para objetos de classe lm. Isso pode ser obtido tranformando o não linear em linear, o que de fato é assumido durante estimação e para muita das inferências.
#-----------------------------------------------------------------------
# Ajusta um modelo linear por aproximação de Taylor.
# plot(residuals(n0) ~ fitted(n0))
# qqnorm(residuals(n0))
exponf <- deriv3(expr = ~f0 + f1 * (1 - exp(-k * x)),
namevec = c("f0", "f1", "k"),
function.arg = function(x, f0, f1, k) {
NULL
})
c0 <- coef(n0)
at_theta <- exponf(x = turk0$A,
f0 = c0["f0"],
f1 = c0["f1"],
k = c0["k"])
f_grad <- attr(at_theta, "gradient")
unique(f_grad)## f0 f1 k
## [1,] 1 0.0000000 0.000000
## [2,] 1 0.2479014 5.362523
## [3,] 1 0.5094459 8.744225
## [4,] 1 0.6800375 9.125432
## [5,] 1 0.8638795 6.793848
## [6,] 1 0.9564466 3.415934# Passa a matriz gradiente para a lm().
m0 <- lm(Gain ~ 0 + f_grad, data = turk0)
# Gráficos de resíduos.
par(mfrow = c(2, 2))
plot(m0)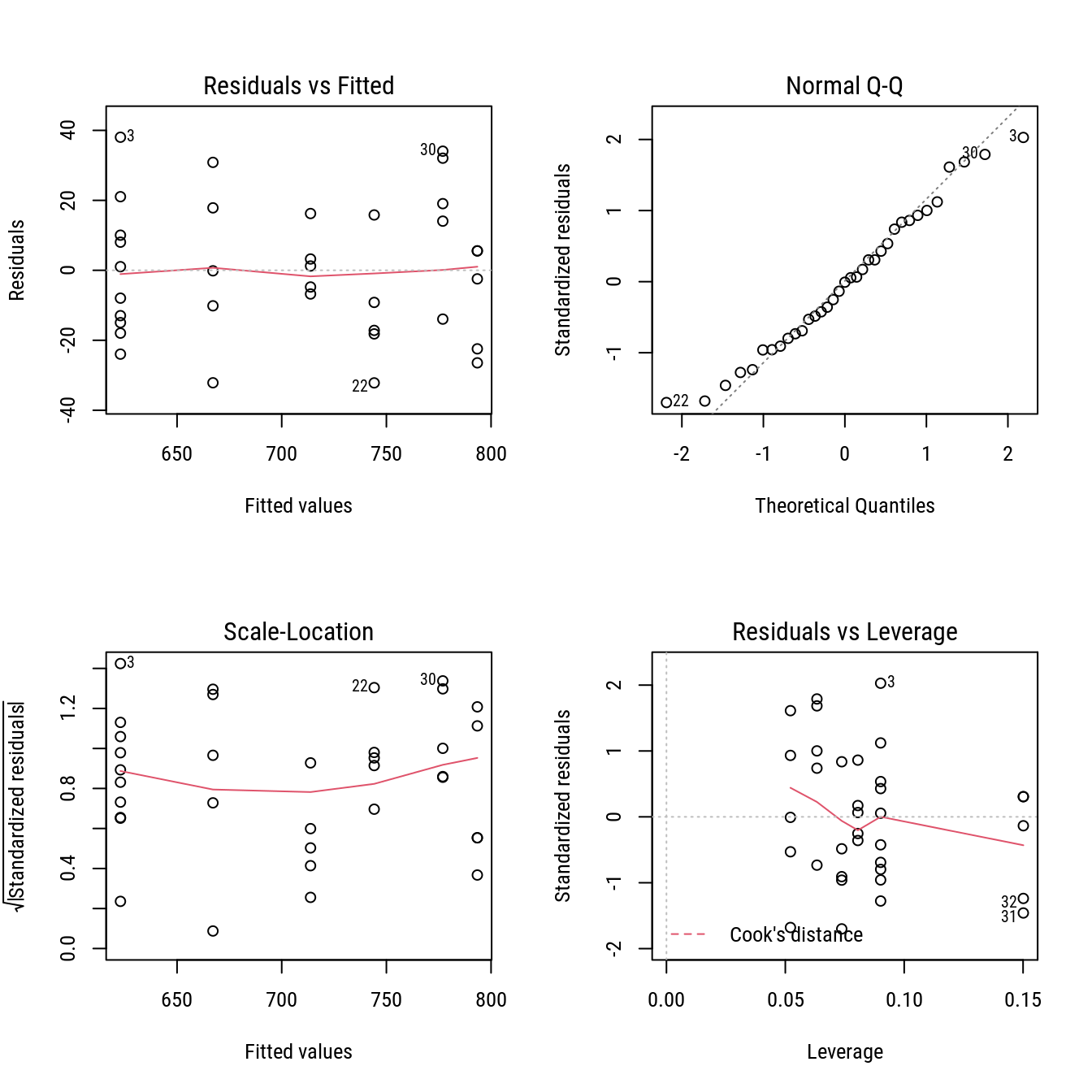
layout(1)Em versões anteriores do pacote nls2 havia a função as as.lm() que permitia a conversão de classe nls para lm facilitando para o usuário o tarefa de análise dos resíduos. Infelizmente, a função foi removida do pacote.
#-----------------------------------------------------------------------
# Usa a função `as.lm()`.
summary(as.lm(n0))##
## Call:
## lm(formula = Gain ~ f0 + f1 + k - 1, data = structure(list(Gain = c(644L,
## 631L, 661L, 624L, 633L, 610L, 615L, 605L, 608L, 599L, 698L, 667L,
## 657L, 685L, 635L, 730L, 715L, 717L, 709L, 707L, 735L, 712L, 726L,
## 760L, 727L, 809L, 796L, 763L, 791L, 811L, 767L, 771L, 799L, 799L,
## 791L), f0 = c(0.999999994057602, 0.999999994057602, 0.999999994057602,
## 0.999999994057602, 0.999999994057602, 0.999999994057602, 0.999999994057602,
## 0.999999994057602, 0.999999994057602, 0.999999994057602, 0.999999994057602,
## 0.999999994057602, 0.999999994057602, 0.999999994057602, 0.999999994057602,
## 0.999999994057602, 0.999999994057602, 0.999999994057602, 0.999999994057602,
## 0.999999994057602, 0.999999994057602, 0.999999994057602, 0.999999994057602,
## 0.999999994057602, 0.999999994057602, 1.00000000630465, 1.00000000630465,
## 1.00000000630465, 1.00000000630465, 1.00000000630465, 0.999999994057602,
## 0.999999994057602, 0.999999994057602, 0.999999994057602, 0.999999994057602
## ), f1 = c(0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0.247901412785238, 0.247901412785238,
## 0.247901412785238, 0.247901412785238, 0.247901412785238, 0.509445871486249,
## 0.509445871486249, 0.509445871486249, 0.509445871486249, 0.509445871486249,
## 0.680037532505223, 0.680037532505223, 0.680037532505223, 0.680037532505223,
## 0.680037532505223, 0.863879581455345, 0.863879581455345, 0.863879581455345,
## 0.863879581455345, 0.863879581455345, 0.956446539871433, 0.956446539871433,
## 0.956446539871433, 0.956446539871433, 0.956446539871433), k = c(0,
## 0, 0, 0, 0, 0, 0, 0, 0, 0, 5.36252240210377, 5.36252240210377,
## 5.36252240210377, 5.36252240210377, 5.36252240210377, 8.74422397589386,
## 8.74422397589386, 8.74422397589386, 8.74422397589386, 8.74422397589386,
## 9.12543249905286, 9.12543249905286, 9.12543249905286, 9.12543249905286,
## 9.12543249905286, 6.79384811123702, 6.79384811123702, 6.79384811123702,
## 6.79384811123702, 6.79384811123702, 3.4159343489768, 3.4159343489768,
## 3.4159343489768, 3.4159343489768, 3.4159343489768)), class = "data.frame", row.names = c(NA,
## -35L)), offset = fitted(n0))
##
## Residuals:
## Min 1Q Median 3Q Max
## -32.176 -14.452 -0.147 14.939 38.042
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## f0 -5.252e-05 5.901e+00 0 1
## f1 -1.566e-04 1.164e+01 0 1
## k 2.627e-05 1.205e+00 0 1
##
## Residual standard error: 19.66 on 32 degrees of freedom
## Multiple R-squared: 0.9993, Adjusted R-squared: 0.9992
## F-statistic: 1.517e+04 on 3 and 32 DF, p-value: < 2.2e-16par(mfrow = c(2, 2))
plot(as.lm(n0))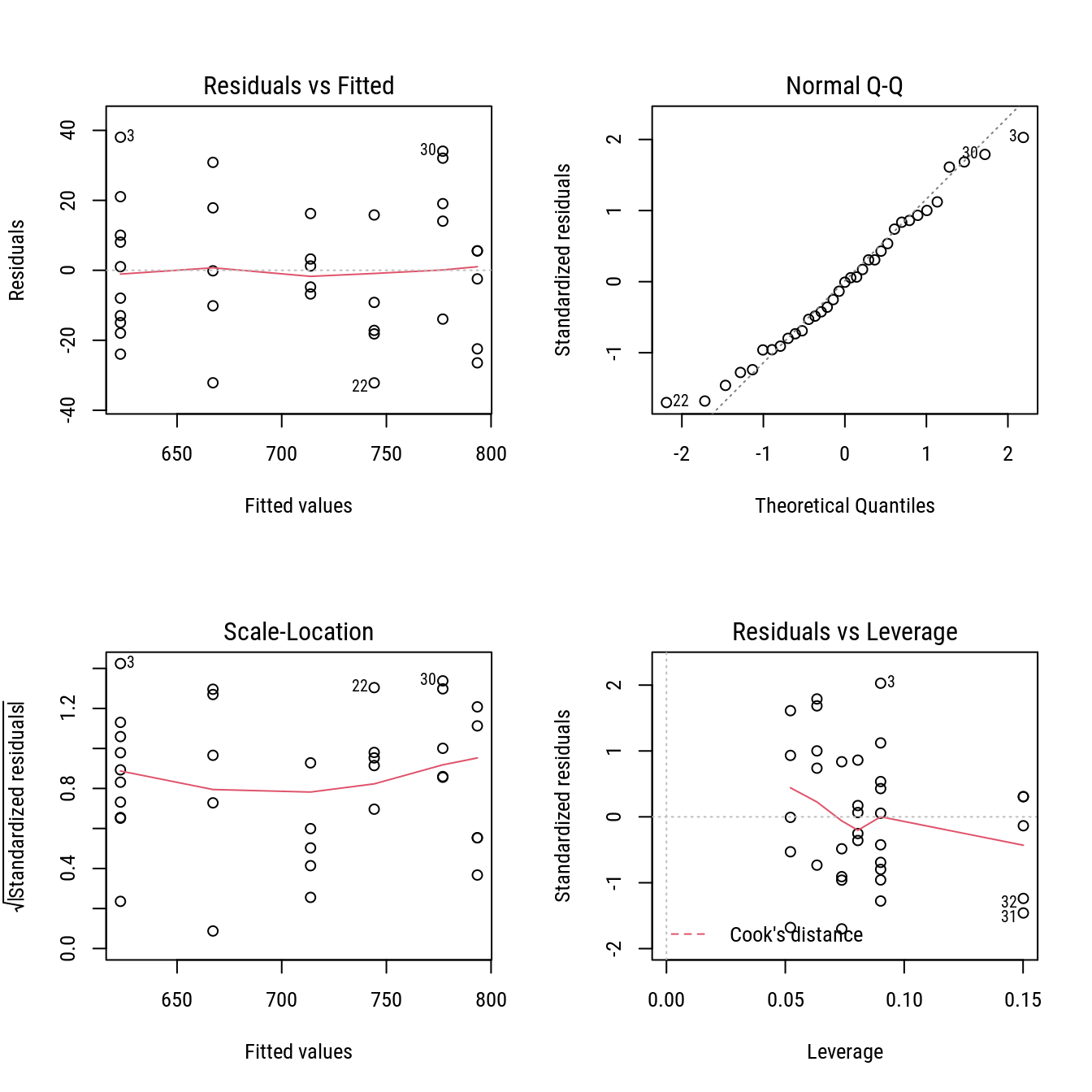
layout(1)3 Coeficiente de determinação
A questão do R2 é polêmica. O que deve ser dito que é R2 alto não indica que os pressupostos foram atendidos da mesma forma que R2 baixo não indica que os pressupostos não foram atendidos. Dessa forma, o modelo, em termos dos seus pressupostos, não pode ser julgado pelo valor do R2. Portanto, o R2 como número isolado não quer dizer muita coisa em termos de diagnóstico. A validade dele como medida é só no momento de comparar modelos.
#-----------------------------------------------------------------------
# R².
# Cuidado! R² não corrigido para a média --> Otimista.
summary(m0)##
## Call:
## lm(formula = Gain ~ 0 + f_grad, data = turk0)
##
## Residuals:
## Min 1Q Median 3Q Max
## -32.176 -14.452 -0.147 14.939 38.042
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## f_gradf0 6.230e+02 5.901e+00 105.57 < 2e-16 ***
## f_gradf1 1.783e+02 1.164e+01 15.32 2.74e-16 ***
## f_gradk 2.624e-05 1.205e+00 0.00 1
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 19.66 on 32 degrees of freedom
## Multiple R-squared: 0.9993, Adjusted R-squared: 0.9992
## F-statistic: 1.517e+04 on 3 and 32 DF, p-value: < 2.2e-16# Corrigido para média.
summary(lm(Gain ~ f_grad, data = turk0))##
## Call:
## lm(formula = Gain ~ f_grad, data = turk0)
##
## Residuals:
## Min 1Q Median 3Q Max
## -32.176 -14.452 -0.147 14.939 38.042
##
## Coefficients: (1 not defined because of singularities)
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 6.230e+02 5.901e+00 105.57 < 2e-16 ***
## f_gradf0 NA NA NA NA
## f_gradf1 1.783e+02 1.164e+01 15.32 2.74e-16 ***
## f_gradk 2.624e-05 1.205e+00 0.00 1
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 19.66 on 32 degrees of freedom
## Multiple R-squared: 0.9226, Adjusted R-squared: 0.9178
## F-statistic: 190.8 on 2 and 32 DF, p-value: < 2.2e-16anova(lm(Gain ~ f_grad, data = turk0))## Analysis of Variance Table
##
## Response: Gain
## Df Sum Sq Mean Sq F value Pr(>F)
## f_grad 2 147497 73749 190.82 < 2.2e-16 ***
## Residuals 32 12367 386
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1# R² ajustado para média: modelo atual em relação ao modelo nulo.
1 - deviance(n0)/deviance(lm(Gain ~ 1, turk0))## [1] 0.9226382# Esse é o jeito mais simples de calcular o R².
cor(turk0$Gain, fitted(n0))^2## [1] 0.9226382#-----------------------------------------------------------------------
# Função feita para obter partição da SQ e R².
R2nls(n0)## $anova
## Df Sum Sq Mean Sq F value Pr(>F)
## 1 regression 2 147497.33 73748.6628 190.8205 0
## 2 residuals 32 12367.42 386.4818 NA NA
##
## $R2
## [1] 0.92263824 AIC, BIC e log-verossimilhança
# Soma de quadrados dos resíduos.
sum(residuals(n0)^2)## [1] 12367.42deviance(n0)## [1] 12367.42# Valor de log-verossimilhança.
n <- length(fitted(n0)) # Número de observações.
sse <- deviance(n0) # Soma de quadrados dos resíduos.
-n/2 * log(2 * pi) - n/2 * log(sse/n) - n/2## [1] -152.3436logLik(n0)## 'log Lik.' -152.3436 (df=4)# Número de parâmetros considerando o de variância também.
p <- length(coef(n0)) + 1
# Valor da medida AIC.
AIC(n0)## [1] 312.68722 * p - 2 * c(logLik(n0))## [1] 312.6872# Valor da medida BIC.
BIC(n0)## [1] 318.9086log(n) * p - 2 * c(logLik(n0))## [1] 318.90865 PRESS
A medida PRESS significa prediction error sum of squares. Ela é uma medida que corresponde a soma de quadrados dos desvios sem a \(i\)-esima observação, ou seja \[ \text{PRESS} = \sum_{i = 1}^n (y_i - \hat{y}_{i, -i})^2 \] em que \(y_i\) é o valor observado na \(i\)-ésima unidade e \(\hat{y}_{i, -i}\) é o valor predito para esta \(i\)-esima, no entanto, os parâmetros do modelo foram estimados deixando a \(i\)-esima observação de fora. Isso significa que o modelo teve que ser ajustado aos dados \(n\) vezes e cada ajuste feito com um conjunto de \(n - 1\) observações. O PRESS é uma medida baseada no método leave-one-out.
# Calcula o PRESS.
library(qpcR)
qpcR::PRESS(n0)## .........10.........20.........30.....## $stat
## [1] 14592.07
##
## $residuals
## [1] 23.1007609 8.8277506 41.7704546 1.1436591 11.0233824 -14.2216253 -8.7344688
## [8] -19.7082867 -16.4163488 -26.2916252 32.4987053 -0.1549185 -10.6956966 18.8091699
## [15] -33.8997231 17.5665264 1.3342745 3.4996838 -5.1640075 -7.3307901 -9.8753068
## [22] -34.6078817 -19.5566920 17.0401319 -18.4811989 34.2191498 20.3406606 -14.8879514
## [29] 15.0028721 36.3543264 -31.0075200 -26.3068460 6.4895651 6.4895651 -2.8614309
##
## $P.square
## [1] 0.9087224# Usa Jackknife para obter estimativas sem a i-ésima observação.
jk <- nlstools::nlsJack(n0)$coefjack
head(jk)## f0 f1 k
## [1,] 620.8992 179.6281 7.281972
## [2,] 622.1721 178.7740 7.183214
## [3,] 619.2295 180.7617 7.411662
## [4,] 622.8564 178.3196 7.130056
## [5,] 621.9765 178.9046 7.198400
## [6,] 624.2215 177.4198 7.024250theta <- split(jk, seq_len(nrow(jk)))
theta <- lapply(theta, "names<-", names(coef(n0)))
theta[[1]]## f0 f1 k
## 620.899221 179.628090 7.281972# Conta manual para compreender o método.
# Obtém os resíduos sem a i-ésima observação.
res_out <- mapply(theta = theta,
y = turk0$Gain,
x = turk0$A,
FUN = function(theta, y, x) {
params <- c(as.list(theta), A = x)
haty <- eval(parse(text = formula(n0)[3]), envir = params)
y - haty
})
sum(res_out^2)## [1] 14592.036 Medidas de não linearidade
# Objeto que retorna gradiente e hessiana.
model_d3 <- deriv3(expr = formula(n0)[-2],
namevec = names(coef(n0)),
function.arg = function(A, f0, f1, k) {
NULL
})
# Reajusta o modelo para retornar gradiente e hessiana.
n1 <- update(n0, formula = . ~ model_d3(A, f0, f1, k))
# Medidas de curvatura de Bates & Watts (menor é melhor).
MASS::rms.curv(n1)## Parameter effects: c^theta x sqrt(F) = 0.8631
## Intrinsic: c^iota x sqrt(F) = 0.1076# Função para o vício de Box.
source("http://leg.ufpr.br/~walmes/cursoR/mrnl2013/fun%c3%a7%c3%b5es/viciobox.R")
biasbox## function (nls.obj)
## {
## theta <- summary(nls.obj)$coef[, 1]
## sd.theta <- summary(nls.obj)$coef[, 2]
## F <- attr(nls.obj$m$fitted(), "gradient")
## H <- attr(nls.obj$m$fitted(), "hessian")
## sig <- summary(nls.obj)$sigma
## n <- dim(F)[1]
## FlFi <- t(F) %*% F
## d <- -(sig^2/2) * sapply(1:n, function(x) {
## sum(diag(solve(FlFi) %*% H[x, , ]))
## })
## bias <- as.vector(solve(FlFi) %*% t(F) %*% d)
## names(bias) <- names(coef(nls.obj))
## bias.sd <- 100 * bias/sd.theta
## bias.th <- 100 * bias/theta
## return(list(`viés bruto` = bias, `%viés(theta)` = bias.th,
## `%viés(sd(theta))` = bias.sd))
## }# Vício de Box para os parâmetros.
bias_box <- biasbox(n1)
do.call(rbind, bias_box)## f0 f1 k
## viés bruto -0.06351643 1.3321440 0.06162927
## %viés(theta) -0.01019594 0.7473375 0.86531266
## %viés(sd(theta)) -1.07638703 11.4488560 5.11398305summary(n0)$coefficients## Estimate Std. Error t value Pr(>|t|)
## f0 622.958080 5.900891 105.570165 2.855729e-42
## f1 178.251986 11.635608 15.319524 2.743798e-16
## k 7.122197 1.205113 5.909983 1.408749e-06# 100 * bias_box[[1]]/coef(n0)
# 100 * bias_box[[1]]/summary(n0)$coefficients[, "Std. Error"]7 Ajuste com as médias vs observações
# Obtém as médias e os pesos.
turk0m <- aggregate(Gain ~ A, data = turk0, FUN = mean)
turk0m$n <- with(turk0, tapply(Gain, A, FUN = length))
turk0m## A Gain n
## 1 0.00 623.0 10
## 2 0.04 668.4 5
## 3 0.10 715.6 5
## 4 0.16 732.0 5
## 5 0.28 794.0 5
## 6 0.44 785.4 5n0m <- update(n0, data = turk0m)
n0w <- update(n0, data = turk0m, weights = c(n))
summary(n0)$coefficients## Estimate Std. Error t value Pr(>|t|)
## f0 622.958080 5.900891 105.570165 2.855729e-42
## f1 178.251986 11.635608 15.319524 2.743798e-16
## k 7.122197 1.205113 5.909983 1.408749e-06summary(n0m)$coefficients## Estimate Std. Error t value Pr(>|t|)
## f0 622.924401 11.791193 52.829635 0.0000149375
## f1 178.274096 17.905853 9.956191 0.0021559530
## k 7.124832 1.901943 3.746081 0.0332055229summary(n0w)$coefficients## Estimate Std. Error t value Pr(>|t|)
## f0 622.958079 8.740483 71.272729 6.086854e-06
## f1 178.251985 17.234825 10.342547 1.928244e-03
## k 7.122197 1.785030 3.989959 2.819326e-02R2nls(n0)$R2## [1] 0.9226382R2nls(n0m)$R2 # R² otimista.## [1] 0.97686158 Observações influentes
O conjunto de dados a seguir é de diametro à altura do peito e altura total de árvores. Foram coletados para fazer o inventário florestal que estima o volume de madeira da área. Será feito o ajuste de modelo para relação altura-diâmetro.
#-----------------------------------------------------------------------
# Carregando os dados.
dap <- read.table("http://www.leg.ufpr.br/~walmes/data/dap.txt",
header = TRUE)
names(dap) <- c("d", "h")
dap <- dap[order(dap$d), ]
dapcc <- dap[complete.cases(dap), ]
rownames(dapcc) <- NULL
p0 <- xyplot(h ~ d, dapcc, col = 1,
xlab = "Diâmetro a altura do peito",
ylab = "Altura da árvore")
p0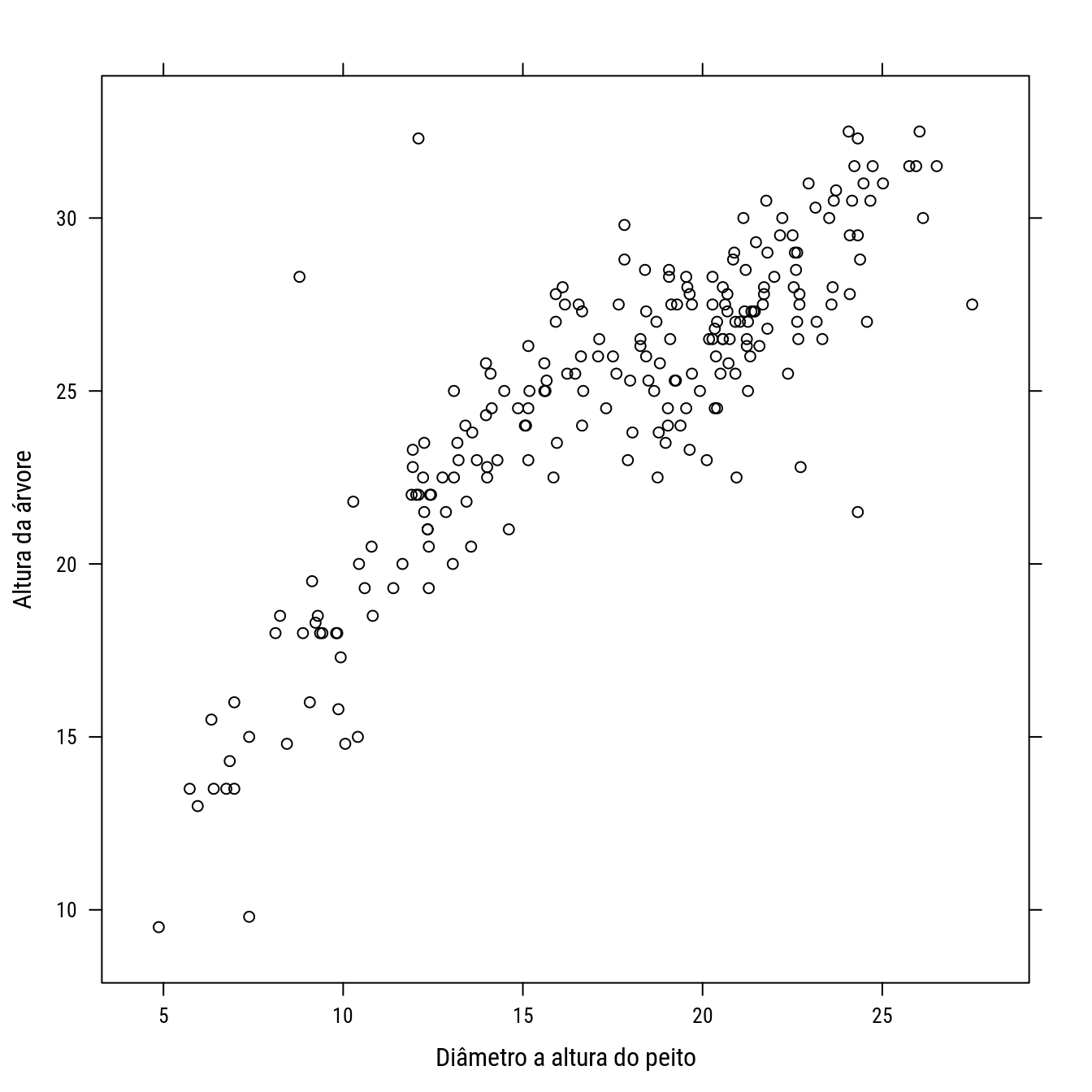
#-----------------------------------------------------------------------
# Análise gráfica do modelo candidato h = b0 * (1 - exp(b1 * d))^b2 para
# obter chutes iniciais. O modelo é extensão do monomolecular.
model <- function(panel) {
plot(h ~ d, dapcc)
with(panel, curve(b0 * (1 - exp(-b1 * x))^b2, add = TRUE,
col = 2))
panel
}
panel <- rp.control()
rp.slider(panel, b1, 0.001, 0.3, initval = 0.09, showvalue = TRUE,
action = model)
rp.slider(panel, b0, 20, 40, initval = 30, showvalue = TRUE,
action = model)
rp.slider(panel, b2, 0.1, 3, initval = 1, showvalue = TRUE,
action = model)
rp.do(panel, action = model)#-----------------------------------------------------------------------
# Ajuste do modelo não linear (com bons chutes).
n0 <- nls(h ~ b0 * (1 - exp(-b1 * d))^b2,
data = dapcc,
start = list(b0 = 35, b1 = 0.1, b2 = 1.05),
trace = FALSE)
summary(n0)##
## Formula: h ~ b0 * (1 - exp(-b1 * d))^b2
##
## Parameters:
## Estimate Std. Error t value Pr(>|t|)
## b0 31.97286 1.38989 23.004 < 2e-16 ***
## b1 0.09815 0.02025 4.846 2.38e-06 ***
## b2 1.09298 0.19803 5.519 9.54e-08 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.101 on 220 degrees of freedom
##
## Number of iterations to convergence: 4
## Achieved convergence tolerance: 5.96e-06p0 +
llayer(with(as.list(coef(n0)),
panel.curve(b0 * (1 - exp(-b1 * x))^b2,
add = TRUE, col = 2, lwd = 3)))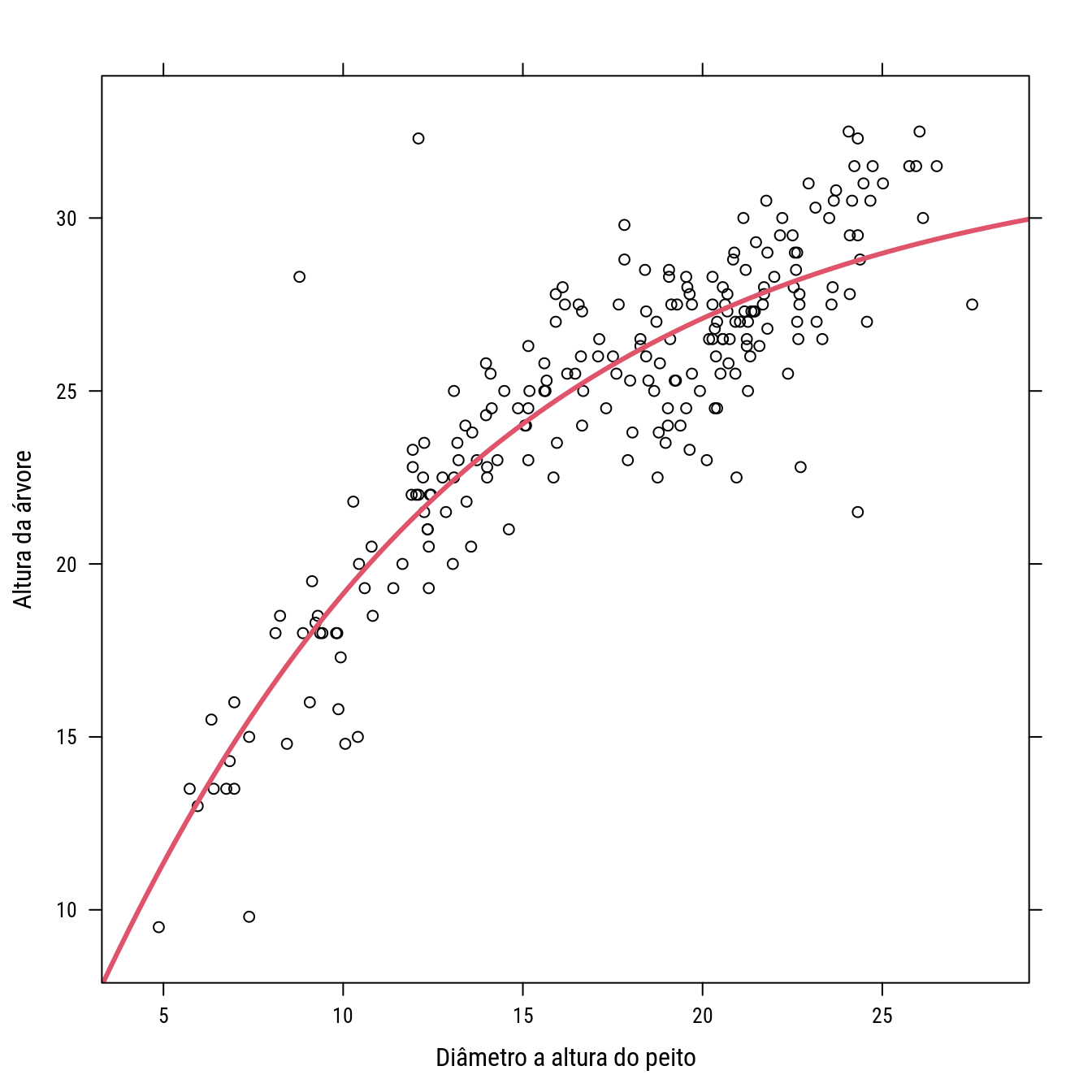
confint.default(n0) # H0: b2 == 1?## 2.5 % 97.5 %
## b0 29.24872362 34.6969974
## b1 0.05845303 0.1378492
## b2 0.70483587 1.4811156confint(n0) # H0: b2 == 1?## 2.5% 97.5%
## b0 29.84399712 36.967448
## b1 0.05372251 0.140280
## b2 0.73983798 1.590308cov2cor(vcov(n0))## b0 b1 b2
## b0 1.0000000 -0.9696839 -0.8972900
## b1 -0.9696839 1.0000000 0.9739108
## b2 -0.8972900 0.9739108 1.0000000#-----------------------------------------------------------------------
# Ajustar um modelo mais parciomonioso, H0: b2 == 1.
n1 <- nls(h ~ b0 * (1 - exp(-b1 * d)),
data = dapcc,
start = list(b0 = 35, b1 = 0.1),
trace = TRUE)## 3123.12 : 35.0 0.1
## 972.6894 : 32.50230218 0.08921745
## 972.4174 : 32.65752887 0.08834877
## 972.4171 : 32.65904395 0.08834915summary(n1)##
## Formula: h ~ b0 * (1 - exp(-b1 * d))
##
## Parameters:
## Estimate Std. Error t value Pr(>|t|)
## b0 32.659044 0.705608 46.28 <2e-16 ***
## b1 0.088349 0.004609 19.17 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.098 on 221 degrees of freedom
##
## Number of iterations to convergence: 3
## Achieved convergence tolerance: 2.767e-08anova(n0, n1)## Analysis of Variance Table
##
## Model 1: h ~ b0 * (1 - exp(-b1 * d))^b2
## Model 2: h ~ b0 * (1 - exp(-b1 * d))
## Res.Df Res.Sum Sq Df Sum Sq F value Pr(>F)
## 1 220 971.49
## 2 221 972.42 -1 -0.92716 0.21 0.6473p0 + llayer(with(as.list(coef(n0)),
panel.curve(b0 * (1 - exp(-b1 * x))^b2,
add = TRUE, col = 2))) +
llayer(with(as.list(coef(n1)),
panel.curve(b0 * (1 - exp(-b1 * x)),
add = TRUE, col = 4)))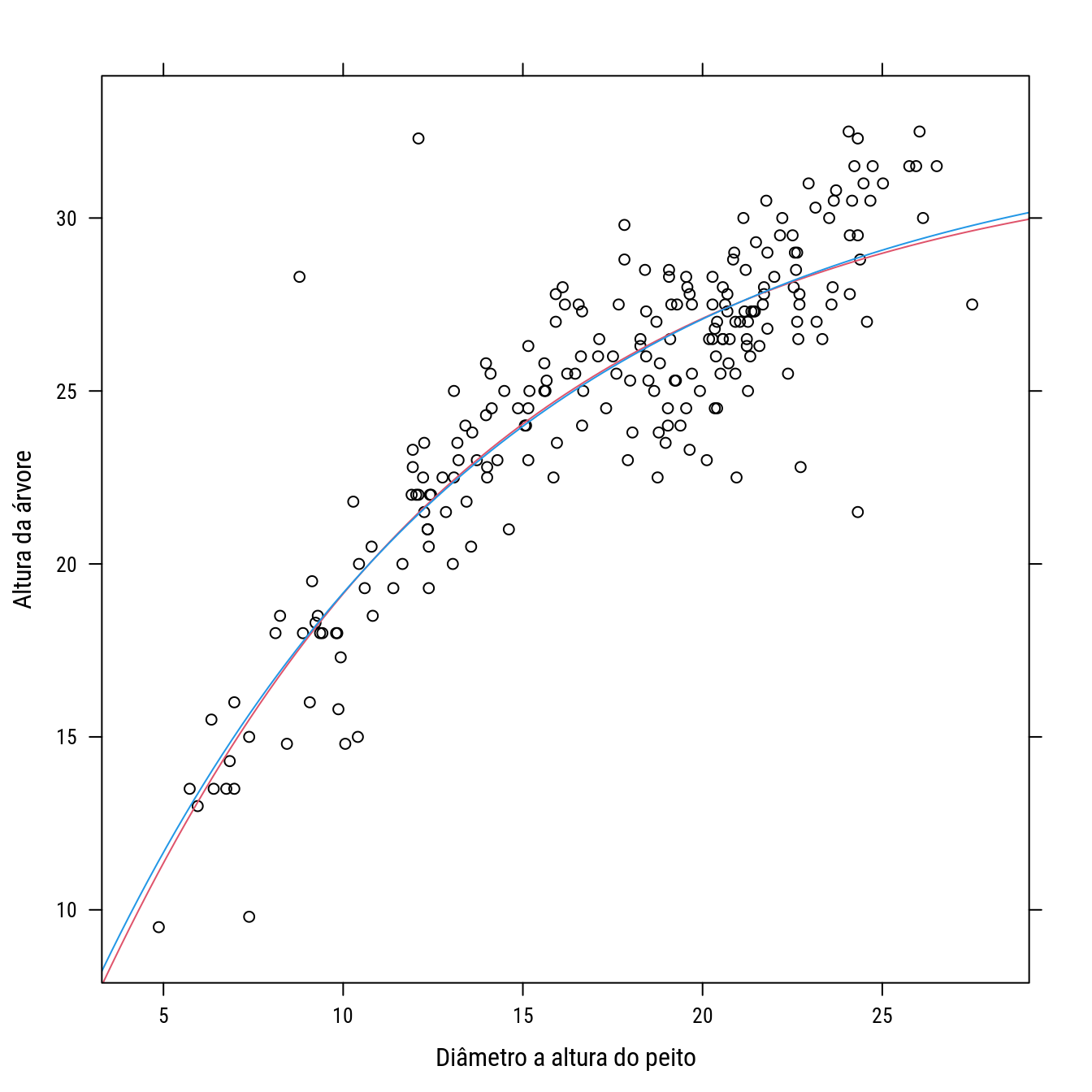
#-----------------------------------------------------------------------
# Análise dos resíduos.
m1 <- as.lm(n1)
par(mfrow = c(2, 2))
plot(m1)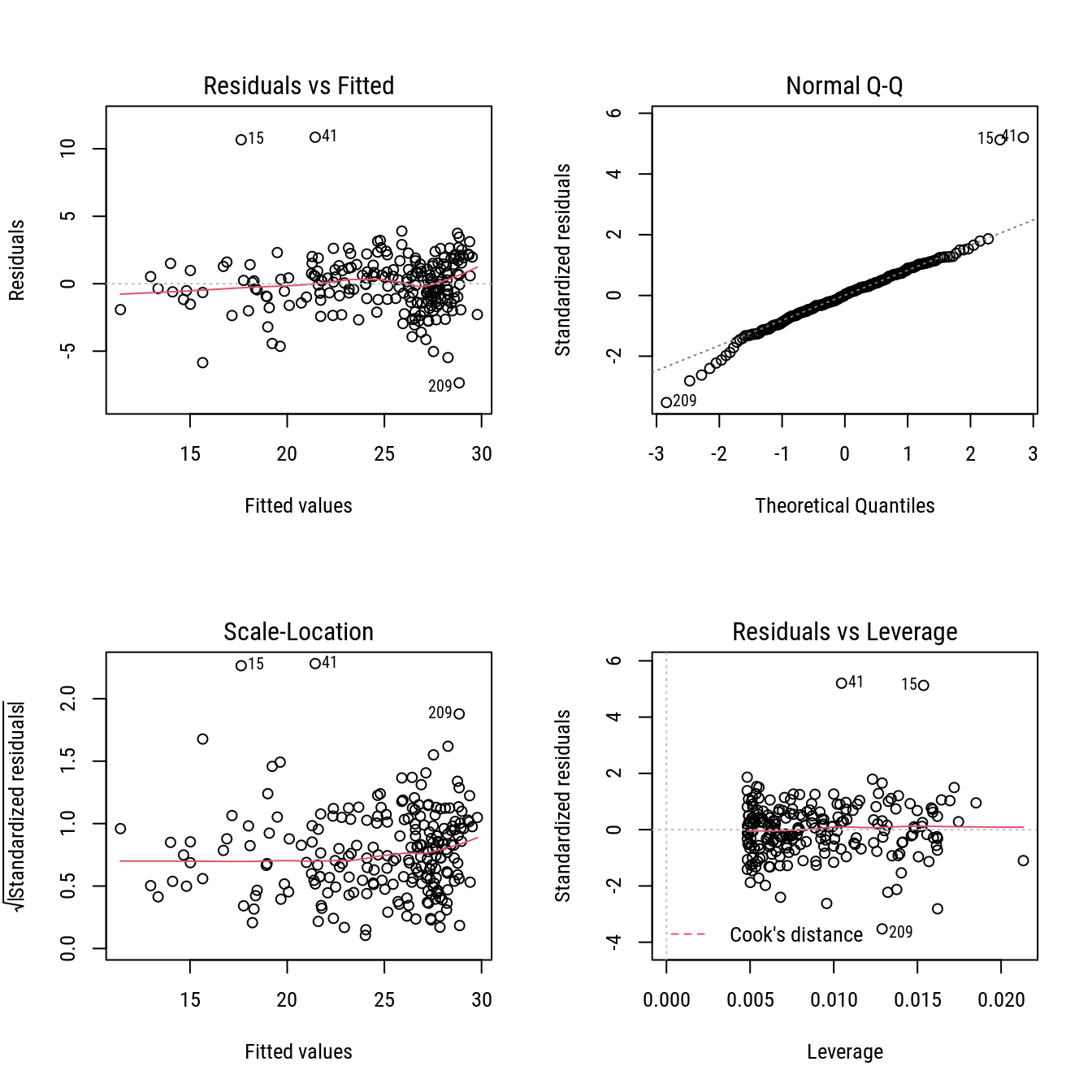
layout(1)
# Medidas de influência usadas para modelos lineares.
m1$call <- NULL
im <- influence.measures(m1)
summary(im)## Potentially influential observations of
## NULL :
##
## dfb.b0 dfb.b1 dffit cov.r cook.d hat
## 10 0.30 -0.35 -0.37_* 0.95_* 0.07 0.02
## 15 -0.54 0.63 0.68_* 0.80_* 0.21 0.02
## 41 -0.37 0.47 0.57_* 0.79_* 0.14 0.01
## 160 -0.14 0.09 -0.20 0.96_* 0.02 0.01
## 194 -0.21 0.17 -0.26 0.96_* 0.03 0.01
## 209 -0.37 0.30 -0.41_* 0.91_* 0.08 0.01str(im)## List of 3
## $ infmat: num [1:223, 1:6] 0.0945 -0.0269 0.0183 -0.0776 0.031 ...
## ..- attr(*, "dimnames")=List of 2
## .. ..$ : chr [1:223] "1" "2" "3" "4" ...
## .. ..$ : chr [1:6] "dfb.b0" "dfb.b1" "dffit" "cov.r" ...
## $ is.inf: logi [1:223, 1:6] FALSE FALSE FALSE FALSE FALSE FALSE ...
## ..- attr(*, "dimnames")=List of 2
## .. ..$ : chr [1:223] "1" "2" "3" "4" ...
## .. ..$ : chr [1:6] "dfb.b0" "dfb.b1" "dffit" "cov.r" ...
## $ call : NULL
## - attr(*, "class")= chr "infl"rem <- im$is.inf[, "dffit"]
#-----------------------------------------------------------------------
# Removendo os outliers.
plot(h ~ d, dapcc)
with(dapcc[rem, ], points(h ~ d, pch = 3, col = 2))
n2 <- update(n1, data = dapcc[!rem, ])## 2821.242 : 35.0 0.1
## 651.5091 : 33.0299464 0.0847141
## 647.8831 : 33.36370613 0.08366757
## 647.8817 : 33.36695226 0.08366804summary(n2)##
## Formula: h ~ b0 * (1 - exp(-b1 * d))
##
## Parameters:
## Estimate Std. Error t value Pr(>|t|)
## b0 33.366952 0.647151 51.56 <2e-16 ***
## b1 0.083668 0.003758 22.27 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.728 on 217 degrees of freedom
##
## Number of iterations to convergence: 3
## Achieved convergence tolerance: 6.599e-08R2nls(n1)$R2## [1] 0.7835906R2nls(n2)$R2## [1] 0.8453427rbind(coef(n1), coef(n2))## b0 b1
## [1,] 32.65904 0.08834915
## [2,] 33.36695 0.08366804#-----------------------------------------------------------------------
# Vendo o resultado nos resíduos e na curva predita.
m2 <- as.lm(n2)
par(mfrow = c(2, 2))
plot(m2)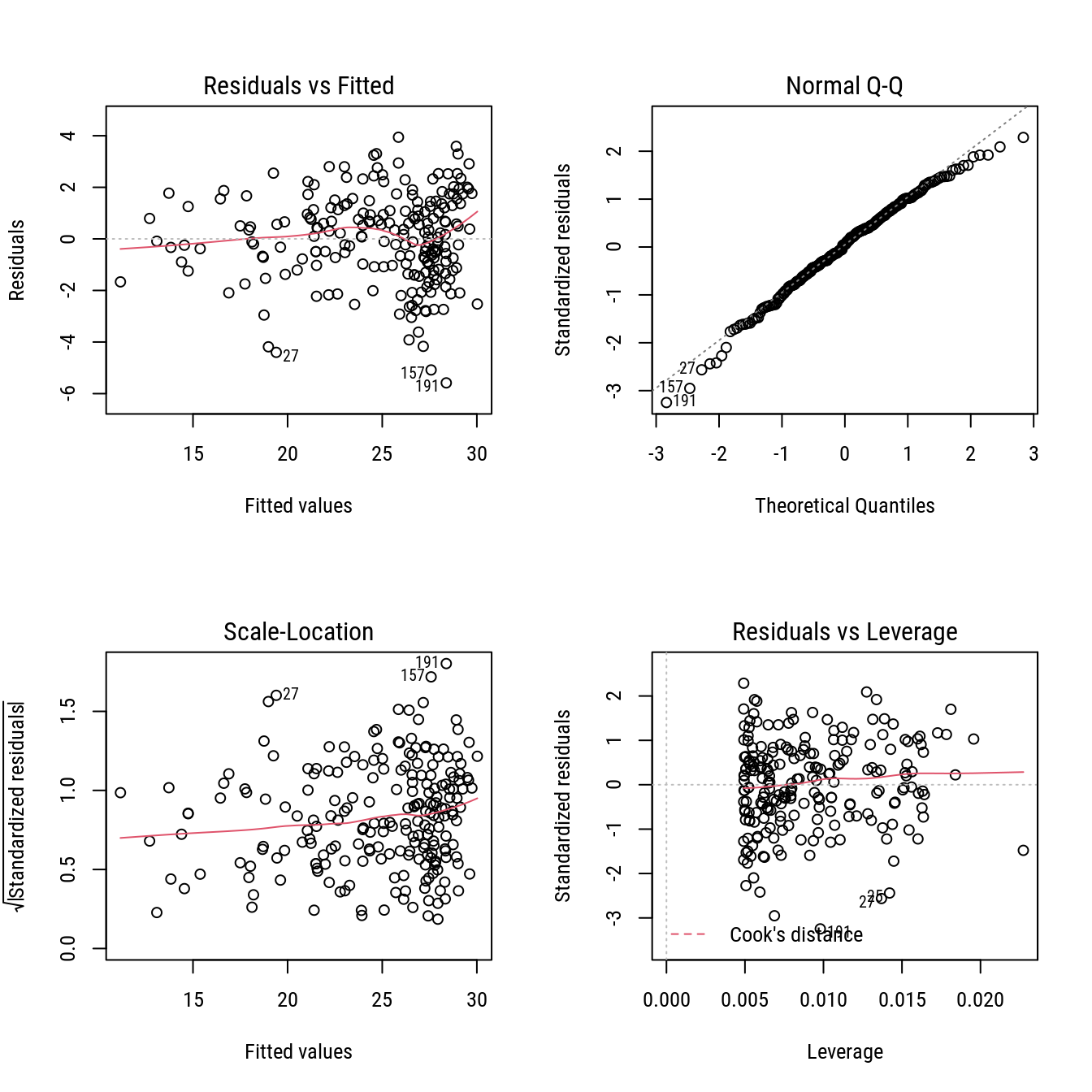
layout(1)
p0 +
llayer(with(as.list(coef(n1)),
panel.curve(b0 * (1 - exp(-b1 * x)),
add = TRUE, col = 4))) +
llayer(with(as.list(coef(n2)),
panel.curve(b0 * (1 - exp(-b1 * x)),
add = TRUE, col = 3)))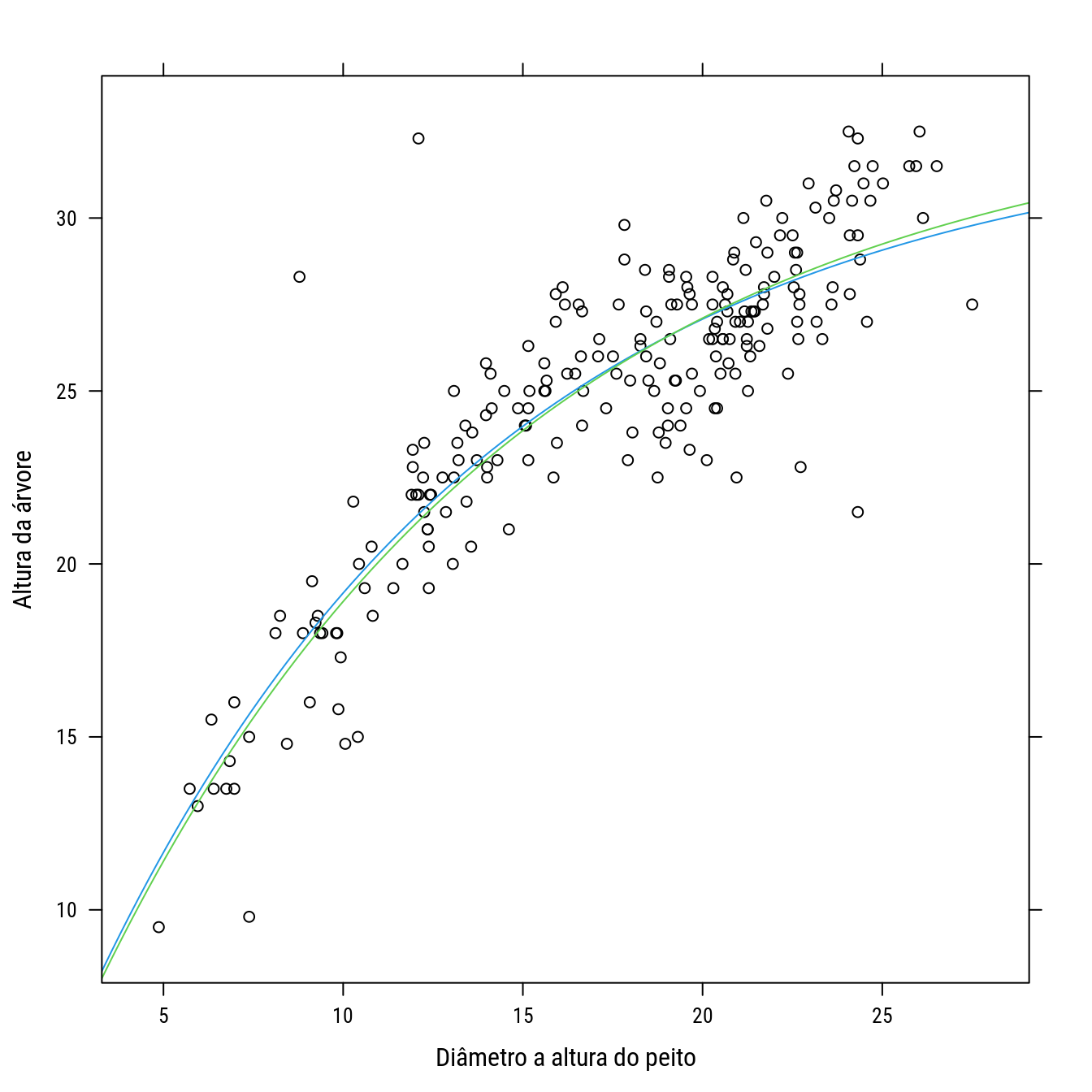
#-----------------------------------------------------------------------9 Autocorrelação serial
#-----------------------------------------------------------------------
# Perda de peso em dieta.
data(wtloss, package = "MASS")
xyplot(Weight ~ Days,
data = wtloss,
type = c("p", "smooth"),
col = 1)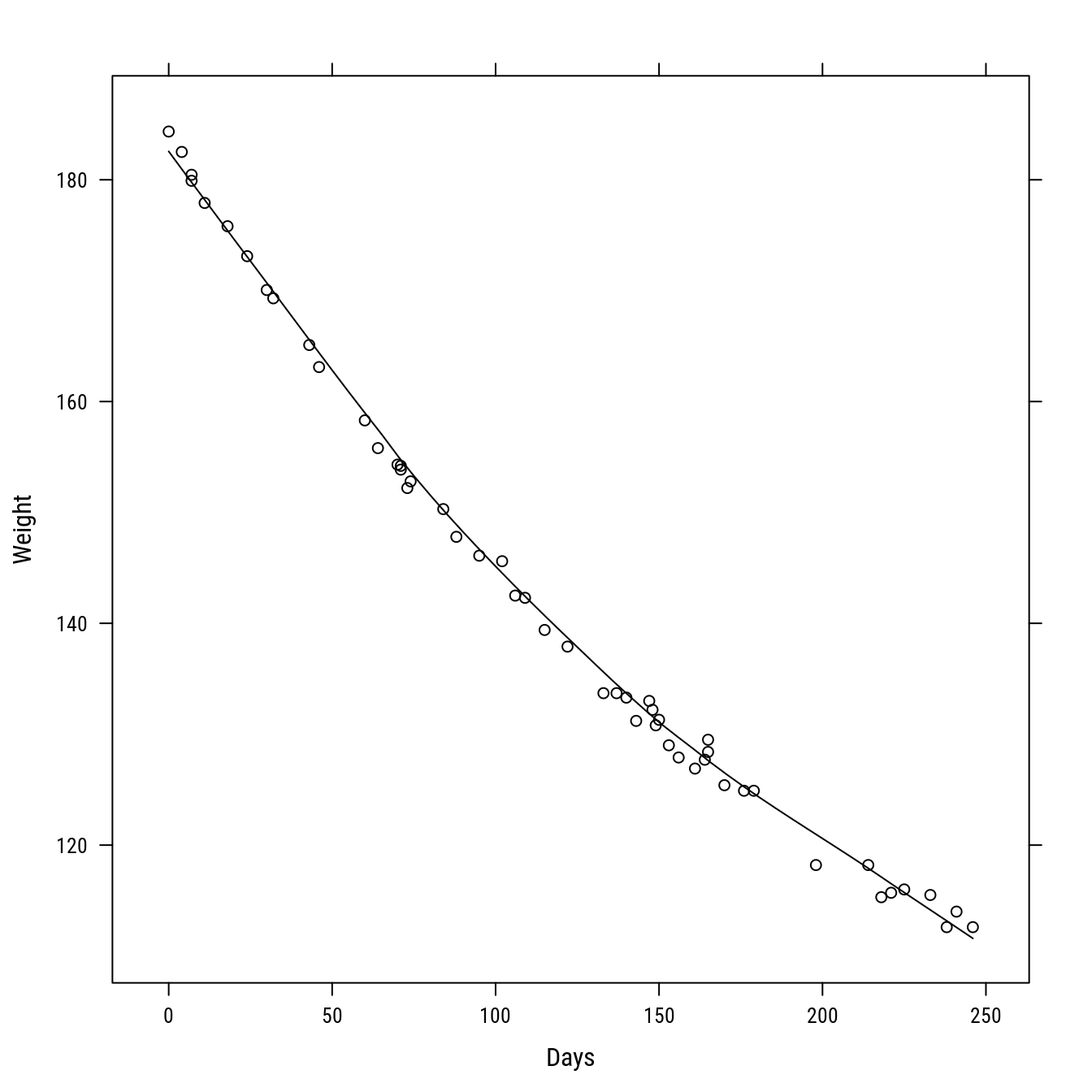
#-----------------------------------------------------------------------
# Modelo
# f0+f1*2^(-x/K)
# * f0: assíntota, peso final após estabilização
# * f1: total de peso à perder, f0+f1 é intercepto ou peso inicial
# * K: tempo para se perder metade do passível de perder, 0.5*(f1-f0)
model <- function(panel) {
plot(Weight ~ Days, data = wtloss,
xlab = "Dias em dieta",
ylab = "Peso (kg)")
with(panel, {
curve(f0 + f1 * 2^(-x/K), add = TRUE, col = 2)
abline(v = K, h = f0 + 0.5 * f1, col = 2, lty = 2)
})
panel
}
panel <- rp.control()
rp.slider(panel, f0, 70, 140, initval = 120, showvalue = TRUE,
action = model)
rp.slider(panel, f1, 20, 200, initval = 50, showvalue = TRUE,
action = model)
rp.slider(panel, K, 0, 250, initval = 150, showvalue = TRUE,
action = model)
rp.do(panel, action = model)#-----------------------------------------------------------------------
# Ajustando o modelo.
n0 <- nls(Weight ~ f0 + f1 * 2^(-Days/K),
data = wtloss,
start = list(f0 = 77, f1 = 107, K = 150))
summary(n0)##
## Formula: Weight ~ f0 + f1 * 2^(-Days/K)
##
## Parameters:
## Estimate Std. Error t value Pr(>|t|)
## f0 81.374 2.269 35.86 <2e-16 ***
## f1 102.684 2.083 49.30 <2e-16 ***
## K 141.910 5.295 26.80 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.8949 on 49 degrees of freedom
##
## Number of iterations to convergence: 3
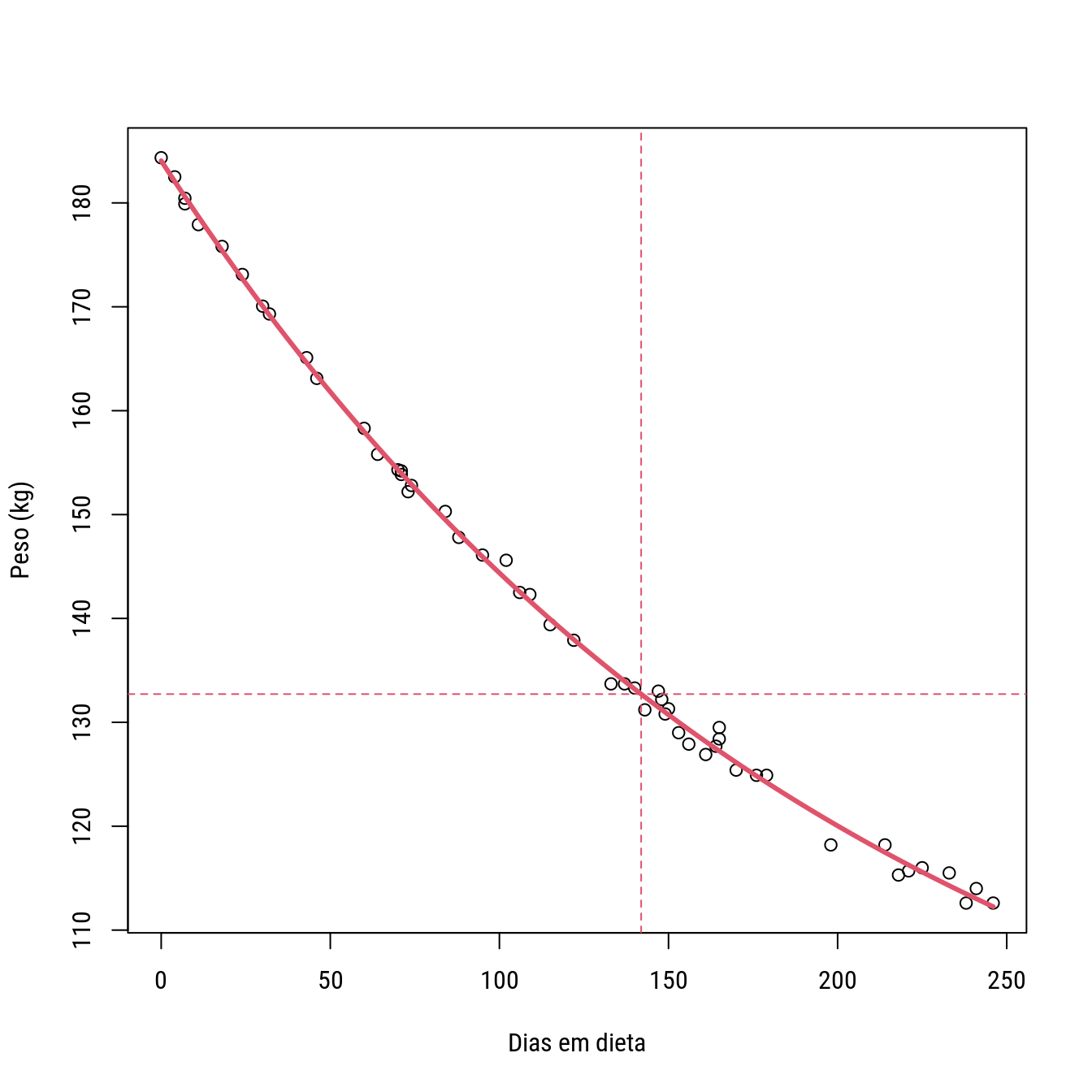
## Achieved convergence tolerance: 5.837e-08plot(Weight ~ Days, data = wtloss,
xlab = "Dias em dieta", ylab = "Peso (kg)")
with(as.list(coef(n0)), {
curve(f0 + f1 * 2^(-x/K), add = TRUE, col = 2, lwd = 3)
abline(v = K, h = f0 + 0.5 * f1, col = 2, lty = 2)
})
#-----------------------------------------------------------------------
# Análise dos resíduos.
par(mfrow = c(2, 2))
plot(as.lm(n0))
layout(1)
# Resíduos correlacionados?
plot(acf(residuals(n0)))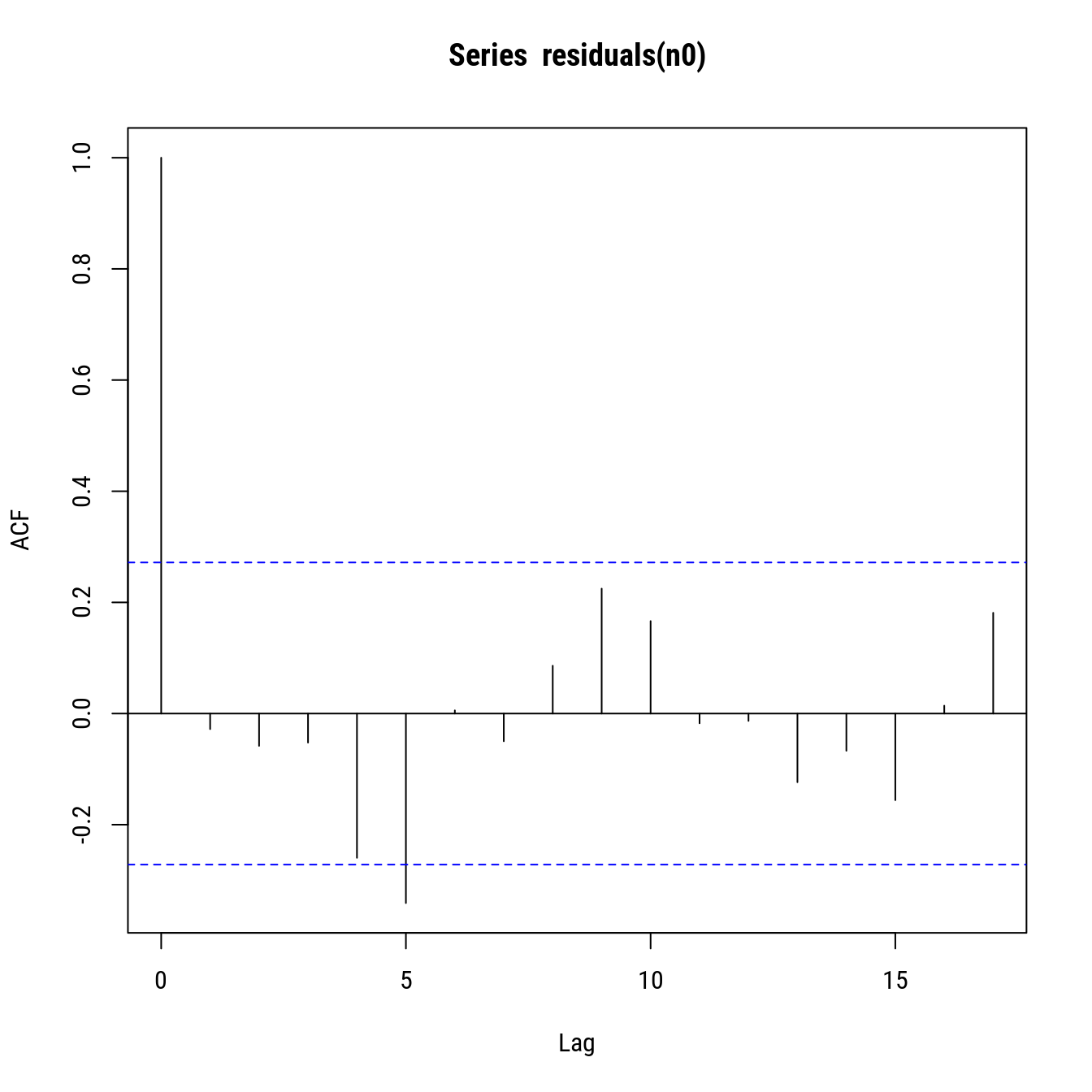
plot(pacf(residuals(n0)))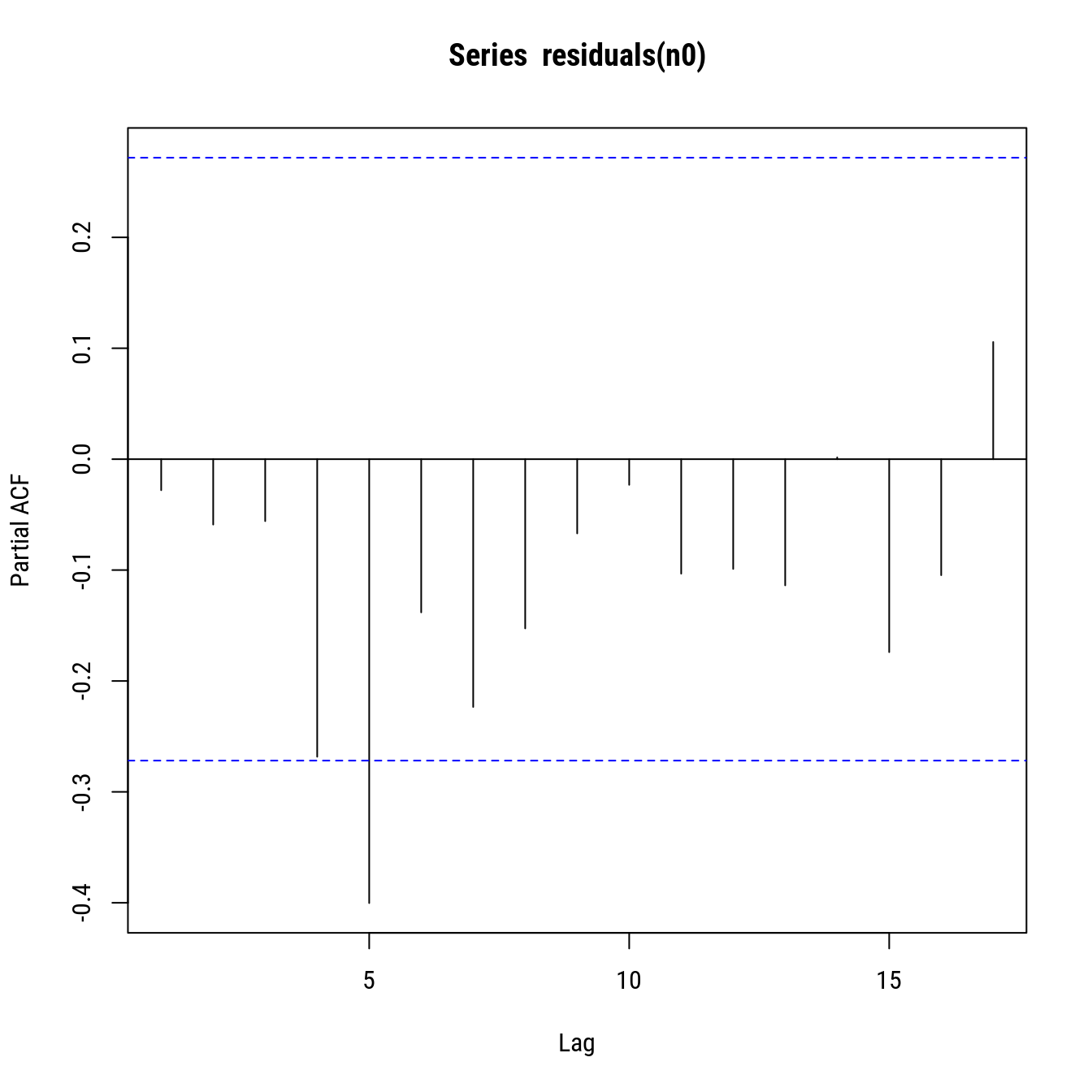
#-----------------------------------------------------------------------
# R² e quadro de anova (partição da SS em modelo e resíduo).
R2nls(n0)## $anova
## Df Sum Sq Mean Sq F value Pr(>F)
## 1 regression 2 22672.0921 1.133605e+04 14153.92 0
## 2 residuals 49 39.2447 8.009122e-01 NA NA
##
## $R2
## [1] 0.998272|
Modelos de Regressão Não Linear: Fundamentos e Aplicações em R leg.ufpr.br/~walmes/cursoR/mrnl |
Prof. Walmes M. Zeviani Departamento de Estatística · UFPR |
