|
Modelos de Regressão Não LinearFundamentos e Aplicações em R |
Ajuste em batelada de modelos não lineares
- http://leg.ufpr.br/~walmes/analises/JPFGardin/Alana/septoriaEC50.html.
- http://leg.ufpr.br/~walmes/pacotes/EACS/articles/teca_cra.html.
- http://leg.ufpr.br/~walmes/pacotes/EACS/articles/pedotrans.html.
- http://leg.ufpr.br/~walmes/pacotes/EACS/articles/maracuja.html.
- http://leg.ufpr.br/~walmes/analises/CECarducci/secagem-solos.html.
1 Dose resposta para Septoria
rm(list = objects())
library(lattice)
library(latticeExtra)
library(nlme)
library(car)
library(tidyverse)
# library(rootSolve)
# library(nlstools)
llayer <- latticeExtra::layer
# source("https://raw.githubusercontent.com/walmes/wzRfun/master/R/panel.cbH.R")1.1 Importação dos dados
#----------------------------------------------------------------------
# Lendo arquivos de dados.
# Url de um arquivo com dados.
url <- "http://www.leg.ufpr.br/~walmes/data/septoriaEC50.txt"
da <- read_tsv(url, comment = "#", col_types = cols())
attr(da, "spec") <- NULL
# Mostra a estrutura do objeto.
str(da)## tibble [1,560 × 6] (S3: spec_tbl_df/tbl_df/tbl/data.frame)
## $ exper : chr [1:1560] "I" "I" "I" "I" ...
## $ fung : chr [1:1560] "Tiofanato" "Tiofanato" "Tiofanato" "Tiofanato" ...
## $ dose : num [1:1560] 0.1 0.1 0.1 0.1 0.1 1 1 1 1 1 ...
## $ rept : num [1:1560] 1 2 3 4 5 1 2 3 4 5 ...
## $ isol : chr [1:1560] "475-6" "475-6" "475-6" "475-6" ...
## $ germ100: num [1:1560] 95 94 95 96 97 92 90 93 92 94 ...# Tabela de frequência.
xtabs(~isol + dose, data = da)## dose
## isol 0 0.1 1 10 100 1000
## 475-1 20 20 20 20 20 20
## 475-2 20 20 20 20 20 20
## 475-3 20 20 20 20 20 20
## 475-4 20 20 20 20 20 20
## 475-5 20 20 20 20 20 20
## 475-6 20 20 20 20 20 20
## 475-7 20 20 20 20 20 20
## 475-8 20 20 20 20 20 20
## 475-9 20 20 20 20 20 20
## 476-1 20 20 20 20 20 20
## 476-2 20 20 20 20 20 20
## 476-3 20 20 20 20 20 20
## 476-4 20 20 20 20 20 20ftable(xtabs(~isol + exper + rept, data = da))## rept 1 2 3 4 5
## isol exper
## 475-1 I 12 12 12 12 12
## II 12 12 12 12 12
## 475-2 I 12 12 12 12 12
## II 12 12 12 12 12
## 475-3 I 12 12 12 12 12
## II 12 12 12 12 12
## 475-4 I 12 12 12 12 12
## II 12 12 12 12 12
## 475-5 I 12 12 12 12 12
## II 12 12 12 12 12
## 475-6 I 12 12 12 12 12
## II 12 12 12 12 12
## 475-7 I 12 12 12 12 12
## II 12 12 12 12 12
## 475-8 I 12 12 12 12 12
## II 12 12 12 12 12
## 475-9 I 12 12 12 12 12
## II 12 12 12 12 12
## 476-1 I 12 12 12 12 12
## II 12 12 12 12 12
## 476-2 I 12 12 12 12 12
## II 12 12 12 12 12
## 476-3 I 12 12 12 12 12
## II 12 12 12 12 12
## 476-4 I 12 12 12 12 12
## II 12 12 12 12 12# Ordenar as linhas.
da <- da %>%
arrange(exper, isol, rept, dose)
#----------------------------------------------------------------------
# Análise exploratória.
xyplot(germ100 ~ dose | isol,
groups = fung,
data = da,
as.table = TRUE,
type = c("p", "a"),
jitter.x = TRUE,
auto.key = TRUE,
scales = list(x = list(log = 10)))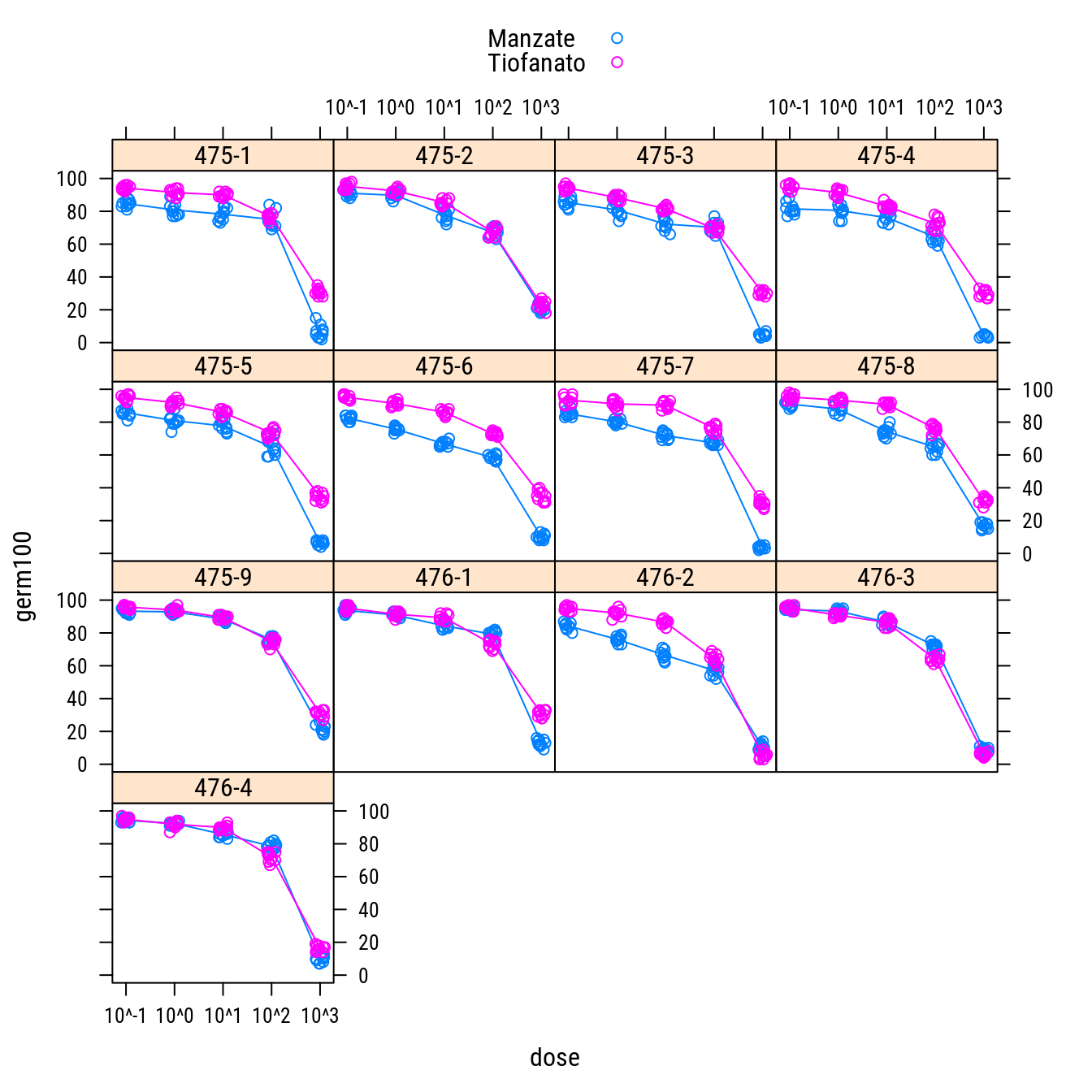
# ATTENTION: Com log a dose zero desaparece pois log(0) não existe!
# Então é melhor usar uma transformação potência.
k <- 0.1
xyplot(germ100 ~ (dose^k) | isol,
groups = fung,
data = da,
jitter.x = TRUE,
auto.key = TRUE,
as.table = TRUE,
type = c("p", "a"))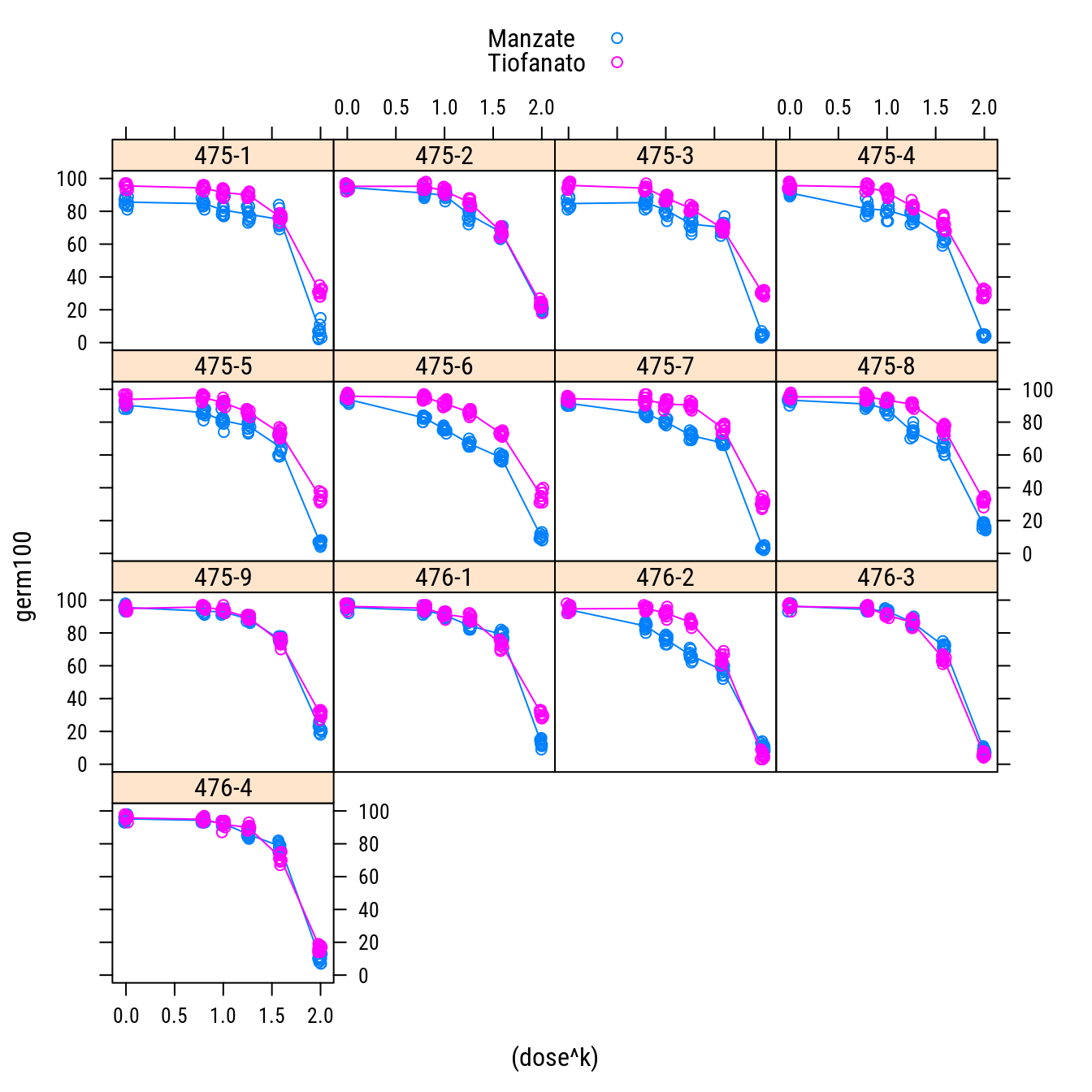
# A escolha de qualquer potência é arbitraria. Será usada k = 0.1 aqui
# porque apresenta uma disposição satisfatoriamente rugular entre as
# doses.
da$x <- da$dose^k1.2 Especificação e estimação do modelo
O modelo considerado para germinação de cada isolado em função da dose para cada fungicida é representado por \[ \begin{aligned} Y|x\, &\sim \text{Normal}(f(x), \sigma^2) \newline f(x)\, &= \theta_{a}\left(1-\left(\dfrac{x}{\theta_{l}}\right)^{\exp\{\theta_{c}\}}\right), \text{ se } x\leq \theta_{l}, \newline f(x)\, &= 0, \text{ se } x> \theta_{l}, \end{aligned} \] em que \(Y\) representa a variável resposta germinação cujo valor médio é uma função \(f\) da dose \(x\) do fungicida descrita por um vetor de parâmetros desconhecidos e a variância é representada por \(\sigma^2\). No modelo não linear, os parâmetros têm o seguinte significado: * \(\theta_{a}\): germinação na ausência de fungicida (dose zero); * \(\theta_{l}\): dose de fungicida acima da qual a germinação é nula, por isso considera-se essa dose como sendo a limítrofe para o desenvolvimento; * \(\theta_{c}\): parâmetro de forma do modelo associado à curvatura.
A partir desse modelo, a dosse correpondente à uma germinação de 50% é obtida por: \[ \begin{aligned} EC_{50} &= \theta_{l} (1-50/\theta_{a})^{\exp\{-\theta_{c}\}}, \end{aligned} \] que é a solução em \(x\) para a expressão do modelo quando \(f(x)=50\).
Após o ajuste do modelo, o erro-padrão, e por consequência, o intervalo de confiança para \(EC_{50}\) pode ser obtido via aplicação do método delta.
#----------------------------------------------------------------------
# Modelo não linear considerado para o caso.
L <- list(tha = 80, thl = 2.4, thc = 1.3)
with(L, {
# Curva.
curve(tha * (1 - (x/thl)^exp(thc)) * (x <= thl) + 0,
from = 0, to = 4,
ylim = c(0, 100), xlab = "x", ylab = "f(x)")
# Anotações.
d <- 0.2
ec50 <- thl * (1 - 50/tha)^exp(-thc)
abline(h = c(50, tha), v = c(ec50, thl), lty = 2)
text(0, tha, label = expression(theta[a]), adj = c(-d, -d))
text(thl, 0, label = expression(theta[l]), adj = c(-d, -d))
text(ec50, 0, label = expression(EC[50]), adj = c(-d, -d))
})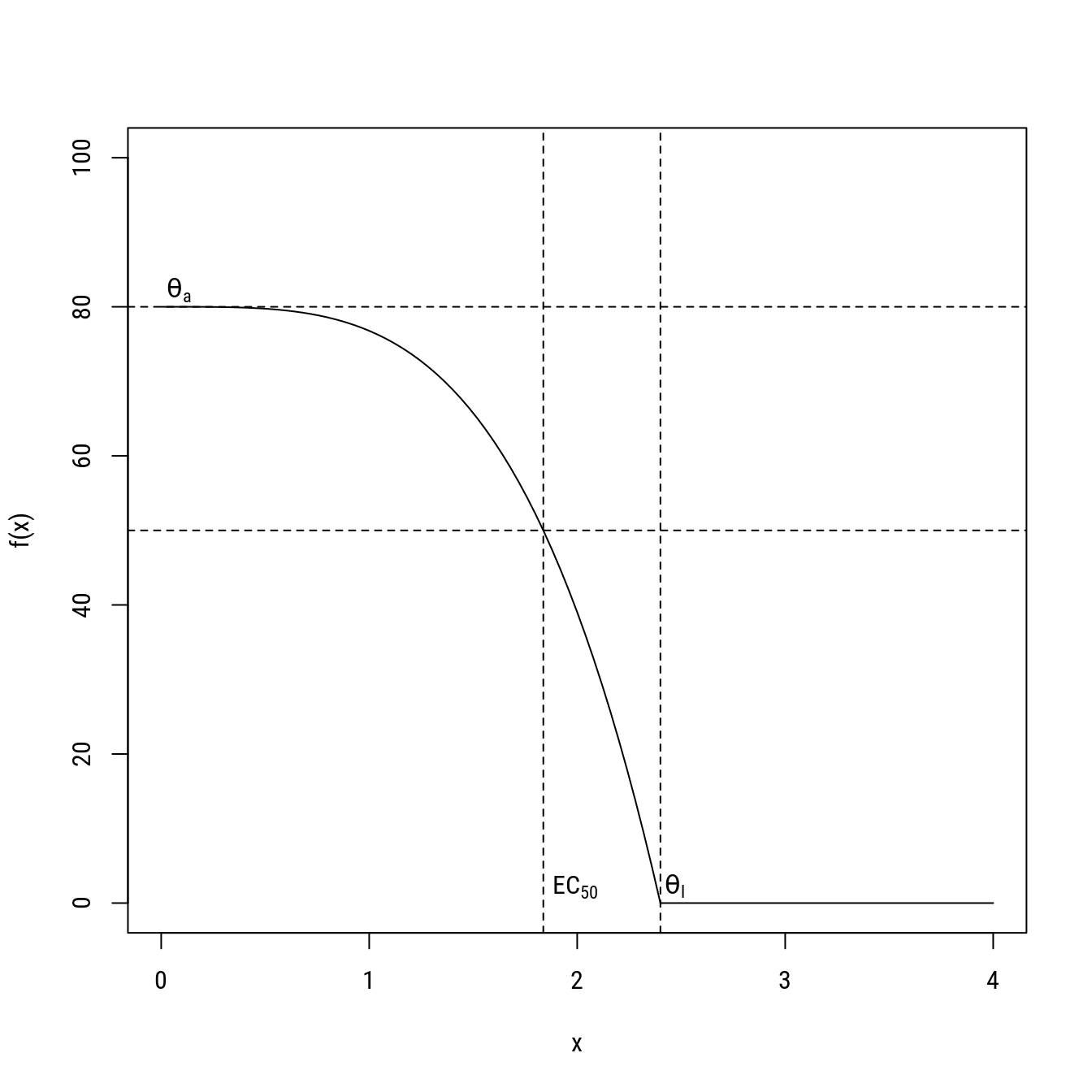
# tha: germinação na dose 0;
# thl: dose acima da qual a germinação é nula;
# thc: fator relacionado à curvatura da função;
# O valor correspondente à uma germinação de 50% é dado por
# x_ec50 = thl * (1 - 50/tha)^exp(-thc)
#----------------------------------------------------------------------
# Aplicando o modelo à todos os casos, modelo de efeito fixo para os
# valores médios observados nas repetições.
# Obtém valores médios.
db <- da %>%
group_by(fung, exper, isol, x) %>%
summarise(g100m = mean(germ100, na.rm = TRUE)) %>%
mutate(caso = interaction(fung, isol, drop = TRUE)) %>%
ungroup()
head(db)## # A tibble: 6 x 6
## fung exper isol x g100m caso
## <chr> <chr> <chr> <dbl> <dbl> <fct>
## 1 Manzate I 475-1 0 85 Manzate.475-1
## 2 Manzate I 475-1 0.794 85.8 Manzate.475-1
## 3 Manzate I 475-1 1 80.4 Manzate.475-1
## 4 Manzate I 475-1 1.26 81 Manzate.475-1
## 5 Manzate I 475-1 1.58 74.6 Manzate.475-1
## 6 Manzate I 475-1 2.00 7.6 Manzate.475-1xyplot(g100m ~ x | isol, groups = fung, data = db, as.table = TRUE)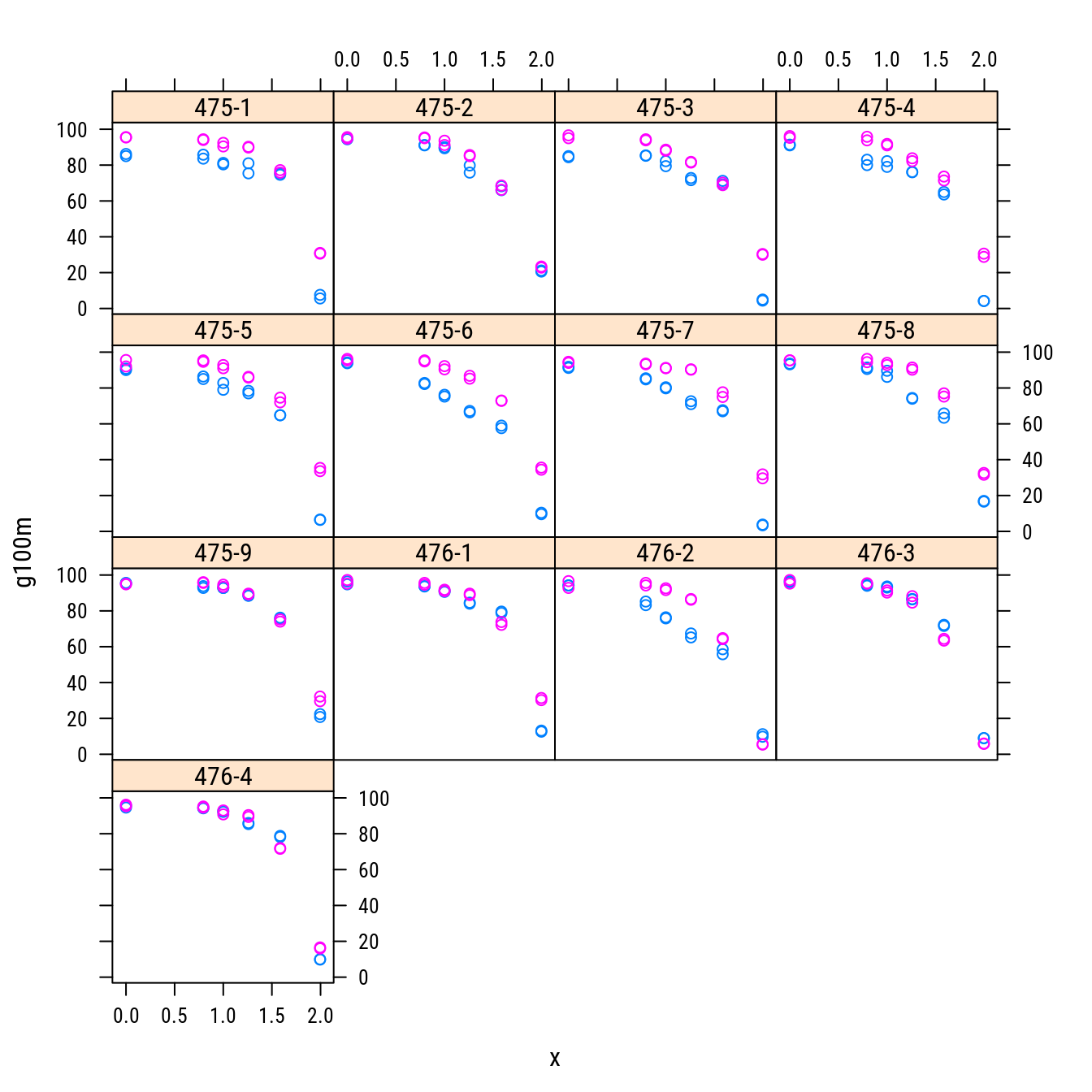
#-----------------------------------------------------------------------
# Ajuste em lote do modelo.
start <- list(tha = 90, thl = 2.1, thc = 1.6)
n00 <- nlsList(g100m ~ tha * (1 - (x/thl)^exp(thc)) * (x <= thl) + 0 | caso,
start = start,
data = db)
#----------------------------------------------------------------------
# Tabelas.
# Dos coeficientes.
coef(n00)## tha thl thc
## Manzate.475-1 82.81517 2.013078 2.242759
## Manzate.475-2 93.48920 2.132101 1.367985
## Manzate.475-3 82.25162 2.012664 1.969935
## Manzate.475-4 85.09161 2.015707 1.691238
## Manzate.475-5 86.55009 2.026815 1.659123
## Manzate.475-6 89.64452 2.096351 1.093903
## Manzate.475-7 85.33309 2.014153 1.705094
## Manzate.475-8 92.74297 2.110189 1.318782
## Manzate.475-9 94.27222 2.086466 1.765540
## Manzate.476-1 92.52534 2.038571 1.962012
## Manzate.476-2 91.05127 2.104647 1.035130
## Manzate.476-3 95.15301 2.032306 1.703534
## Manzate.476-4 93.29823 2.027958 1.949608
## Tiofanato.475-1 94.53497 2.144615 1.698787
## Tiofanato.475-2 96.14151 2.131820 1.417472
## Tiofanato.475-3 95.11726 2.217967 1.302250
## Tiofanato.475-4 95.23327 2.183991 1.434912
## Tiofanato.475-5 94.66575 2.210630 1.487843
## Tiofanato.475-6 95.66668 2.229585 1.416346
## Tiofanato.475-7 93.76357 2.139852 1.733826
## Tiofanato.475-8 95.62572 2.157358 1.653316
## Tiofanato.475-9 95.84372 2.158666 1.595519
## Tiofanato.476-1 95.75385 2.170295 1.528655
## Tiofanato.476-2 95.55963 2.019769 1.555194
## Tiofanato.476-3 96.17787 2.022941 1.513091
## Tiofanato.476-4 95.37629 2.066446 1.673697# Com os extremos do IC.
intervals(n00)## , , tha
##
## lower est. upper
## Manzate.475-1 80.83406 82.81517 84.79629
## Manzate.475-2 90.76767 93.48920 96.21073
## Manzate.475-3 80.14089 82.25162 84.36234
## Manzate.475-4 82.75896 85.09161 87.42426
## Manzate.475-5 84.18488 86.55009 88.91530
## Manzate.475-6 86.54576 89.64452 92.74329
## Manzate.475-7 83.01403 85.33309 87.65215
## Manzate.475-8 89.95342 92.74297 95.53253
## Manzate.475-9 92.00919 94.27222 96.53524
## Manzate.476-1 90.40970 92.52534 94.64097
## Manzate.476-2 87.87797 91.05127 94.22457
## Manzate.476-3 92.83243 95.15301 97.47359
## Manzate.476-4 91.17475 93.29823 95.42170
## Tiofanato.475-1 92.20976 94.53497 96.86018
## Tiofanato.475-2 93.48694 96.14151 98.79607
## Tiofanato.475-3 92.30464 95.11726 97.92988
## Tiofanato.475-4 92.60183 95.23327 97.86470
## Tiofanato.475-5 92.10271 94.66575 97.22879
## Tiofanato.475-6 93.01061 95.66668 98.32275
## Tiofanato.475-7 91.47180 93.76357 96.05534
## Tiofanato.475-8 93.25447 95.62572 97.99698
## Tiofanato.475-9 93.40966 95.84372 98.27778
## Tiofanato.476-1 93.24142 95.75385 98.26628
## Tiofanato.476-2 93.07902 95.55963 98.04025
## Tiofanato.476-3 93.64638 96.17787 98.70936
## Tiofanato.476-4 93.02604 95.37629 97.72654
##
## , , thl
##
## lower est. upper
## Manzate.475-1 2.001656 2.013078 2.024501
## Manzate.475-2 2.093738 2.132101 2.170465
## Manzate.475-3 1.998472 2.012664 2.026857
## Manzate.475-4 1.997795 2.015707 2.033620
## Manzate.475-5 2.007433 2.026815 2.046197
## Manzate.475-6 2.057103 2.096351 2.135598
## Manzate.475-7 1.996678 2.014153 2.031629
## Manzate.475-8 2.074648 2.110189 2.145731
## Manzate.475-9 2.060995 2.086466 2.111937
## Manzate.476-1 2.022553 2.038571 2.054590
## Manzate.476-2 2.063369 2.104647 2.145925
## Manzate.476-3 2.014683 2.032306 2.049929
## Manzate.476-4 2.013455 2.027958 2.042462
## Tiofanato.475-1 2.106007 2.144615 2.183223
## Tiofanato.475-2 2.095180 2.131820 2.168460
## Tiofanato.475-3 2.161375 2.217967 2.274560
## Tiofanato.475-4 2.136005 2.183991 2.231977
## Tiofanato.475-5 2.155377 2.210630 2.265883
## Tiofanato.475-6 2.170131 2.229585 2.289040
## Tiofanato.475-7 2.102031 2.139852 2.177673
## Tiofanato.475-8 2.116089 2.157358 2.198628
## Tiofanato.475-9 2.117277 2.158666 2.200054
## Tiofanato.476-1 2.126021 2.170295 2.214568
## Tiofanato.476-2 2.001352 2.019769 2.038187
## Tiofanato.476-3 2.003632 2.022941 2.042250
## Tiofanato.476-4 2.043858 2.066446 2.089034
##
## , , thc
##
## lower est. upper
## Manzate.475-1 2.0187474 2.242759 2.466770
## Manzate.475-2 1.2154607 1.367985 1.520509
## Manzate.475-3 1.7965410 1.969935 2.143329
## Manzate.475-4 1.5453459 1.691238 1.837131
## Manzate.475-5 1.5131713 1.659123 1.805075
## Manzate.475-6 0.9566831 1.093903 1.231122
## Manzate.475-7 1.5594662 1.705094 1.850721
## Manzate.475-8 1.1736204 1.318782 1.463943
## Manzate.475-9 1.5994373 1.765540 1.931643
## Manzate.476-1 1.7941375 1.962012 2.129886
## Manzate.476-2 0.9007962 1.035130 1.169464
## Manzate.476-3 1.5664191 1.703534 1.840649
## Manzate.476-4 1.7906756 1.949608 2.108540
## Tiofanato.475-1 1.5139656 1.698787 1.883608
## Tiofanato.475-2 1.2662216 1.417472 1.568722
## Tiofanato.475-3 1.1331886 1.302250 1.471311
## Tiofanato.475-4 1.2646439 1.434912 1.605180
## Tiofanato.475-5 1.3017423 1.487843 1.673943
## Tiofanato.475-6 1.2335730 1.416346 1.599119
## Tiofanato.475-7 1.5449628 1.733826 1.922690
## Tiofanato.475-8 1.4706768 1.653316 1.835955
## Tiofanato.475-9 1.4195621 1.595519 1.771476
## Tiofanato.476-1 1.3551198 1.528655 1.702191
## Tiofanato.476-2 1.4295036 1.555194 1.680885
## Tiofanato.476-3 1.3886622 1.513091 1.637519
## Tiofanato.476-4 1.5260339 1.673697 1.821359# Gráfico padrão dos IC.
plot(intervals(n00), as.table = TRUE)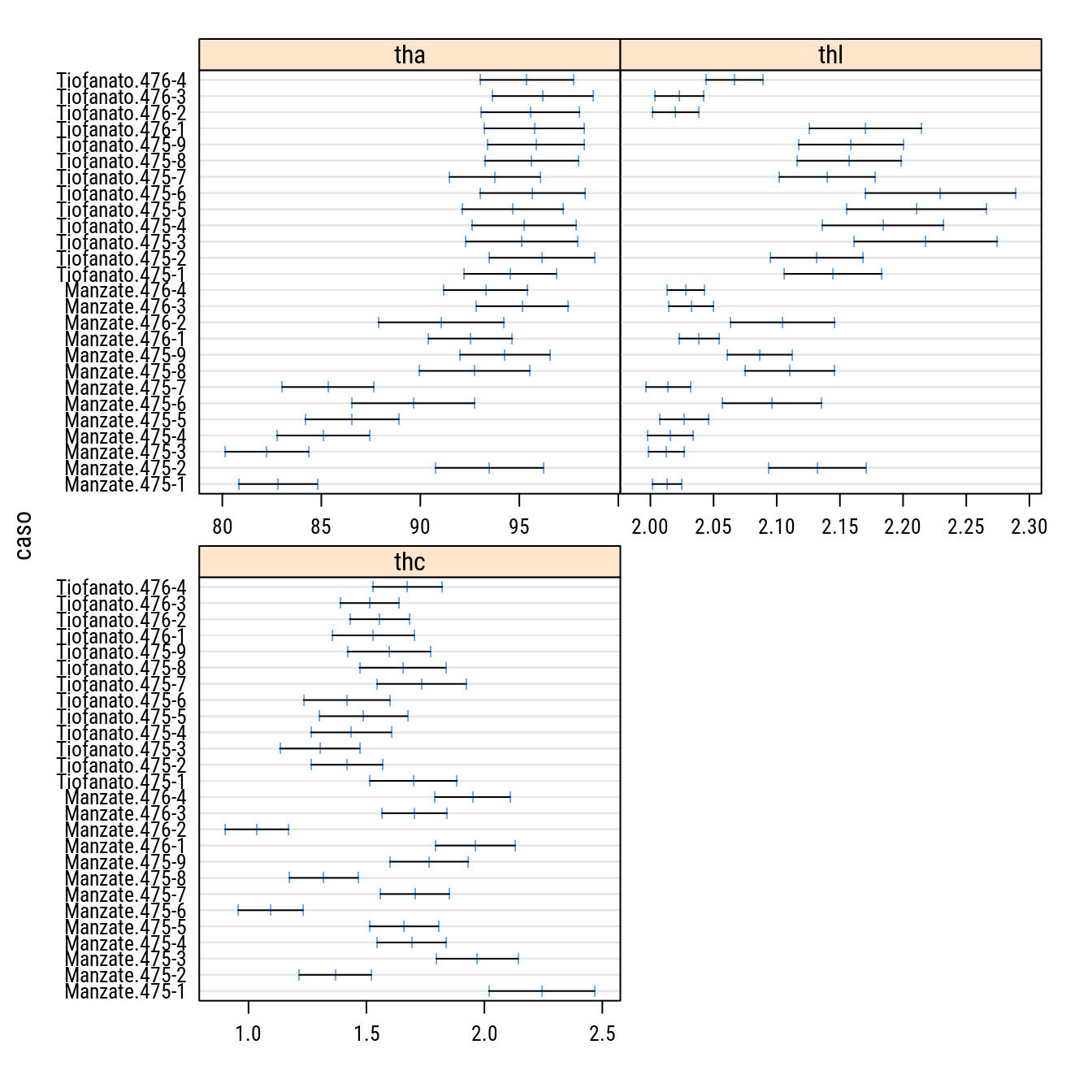
1.3 Calculo da EC50
#----------------------------------------------------------------------
# Calculando o valor da EC50 com intervalo de confiança baseado no
# método delta.
ec50 <- sapply(n00,
simplify = FALSE,
function(i){
dm <- deltaMethod(i, g = "thl * (1 - 50/tha)^exp(-thc)")
return(unlist(dm))
})
ec50 <- as.data.frame(do.call(rbind, ec50))
head(ec50)## Estimate SE 2.5 % 97.5 %
## Manzate.475-1 1.824646 0.01922284 1.786970 1.862322
## Manzate.475-2 1.754597 0.01433332 1.726504 1.782690
## Manzate.475-3 1.766304 0.02649590 1.714373 1.818235
## Manzate.475-4 1.712118 0.02361571 1.665832 1.758404
## Manzate.475-5 1.720155 0.01729734 1.686253 1.754057
## Manzate.475-6 1.595118 0.03249882 1.531422 1.658815#----------------------------------------------------------------------
# Intervalos de confiança dos demais parâmetros.
# IC para os parâmetros do modelo.
ic <- intervals(n00)
#----------------------------------------------------------------------
# Juntar EC50 aos outros, todos no mesmo array.
# Padroniza nomes para fazer junção.
colnames(ec50)[c(3, 1, 4)] <- colnames(ic)
ic <- setNames(apply(ic, MARGIN = 3, as.data.frame),
dimnames(ic)[[3]])
ic <- append(ic, list(ec50 = as.data.frame(ec50))) %>%
map(rownames_to_column, var = "caso") %>%
bind_rows(.id = "param") %>%
rename("est" = "est.")
str(ic)## 'data.frame': 104 obs. of 6 variables:
## $ param: chr "tha" "tha" "tha" "tha" ...
## $ caso : chr "Manzate.475-1" "Manzate.475-2" "Manzate.475-3" "Manzate.475-4" ...
## $ lower: num 80.8 90.8 80.1 82.8 84.2 ...
## $ est : num 82.8 93.5 82.3 85.1 86.6 ...
## $ upper: num 84.8 96.2 84.4 87.4 88.9 ...
## $ SE : num NA NA NA NA NA NA NA NA NA NA ...#----------------------------------------------------------------------
# Gráfico de segmentos para representar o IC 95%.
ic <- ic %>%
separate(col = "caso", into = c("fung", "isol"), remove = FALSE, sep = "\\.") %>%
arrange(param, isol, fung)
ggplot(data = ic,
mapping = aes(y = isol, x = est, color = fung)) +
facet_wrap(facets = ~param, scale = "free_x") +
geom_point(position = position_dodge(0.2)) +
geom_errorbarh(mapping = aes(xmin = lower, xmax = upper),
position = position_dodge(0.2),
height = 0.25)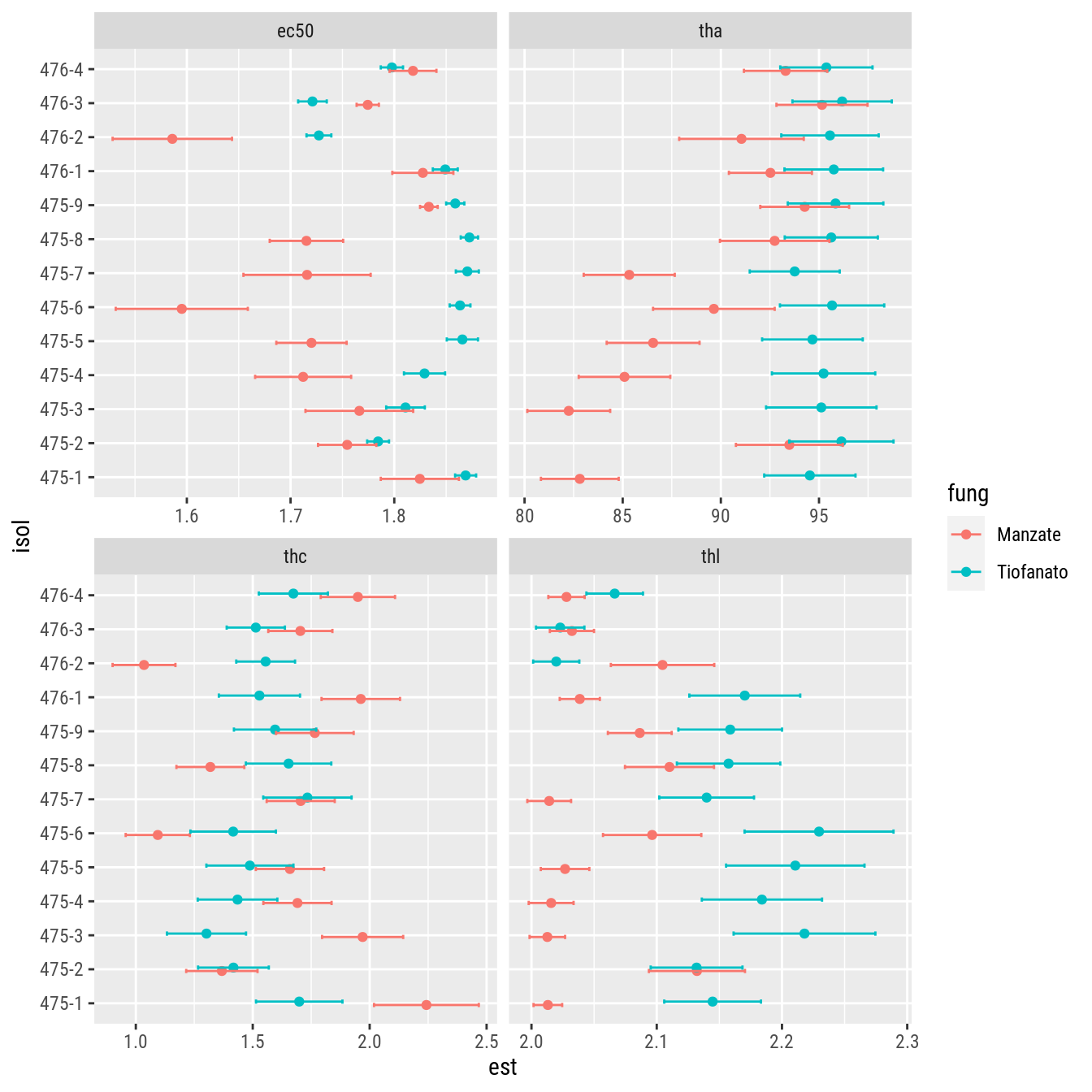
#----------------------------------------------------------------------
# Gráfico só do EC50 e na escala original.
ic %>%
filter(param == "ec50") %>%
mutate_at(c("lower", "est", "upper"), ~ .^(1/k)) %>%
ggplot(mapping = aes(y = isol, x = est, color = fung)) +
geom_point(position = position_dodge(0.2)) +
geom_errorbarh(mapping = aes(xmin = lower, xmax = upper),
position = position_dodge(0.2),
height = 0.25)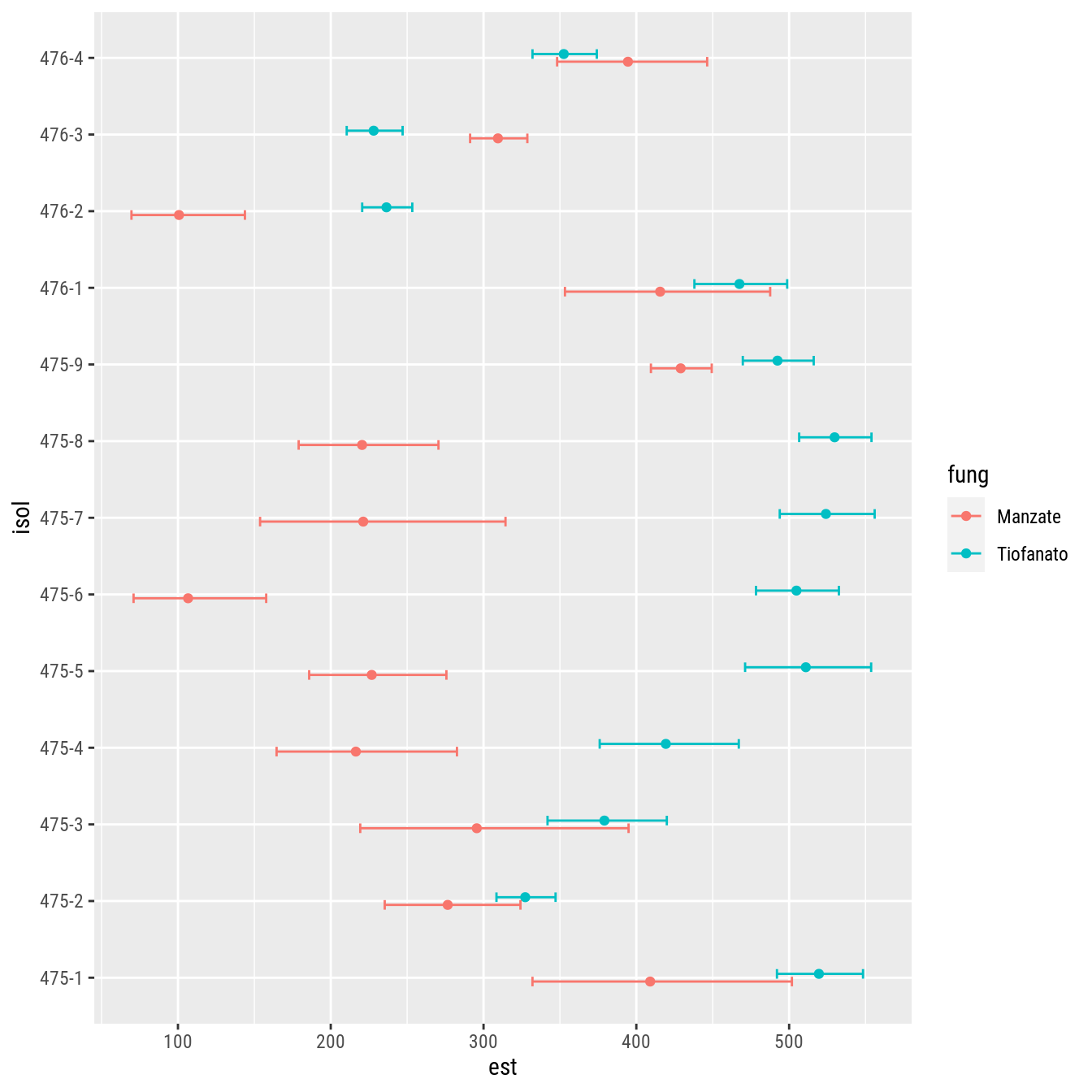
1.4 Curvas ajustadas
#----------------------------------------------------------------------
# Gráfico dos valores preditos pelo modelo regressão não linear
# ajustado.
pred <- data.frame(x = seq(0, 2.5, length.out = 50))
pdto <- map(n00, ~cbind(pred, fit = predict(., newdata = pred))) %>%
bind_rows(.id = "caso") %>%
separate(col = "caso", into = c("fung", "isol"), remove = FALSE, sep = "\\.")#----------------------------------------------------------------------
# Sobrepondo os gráficos e adicionando uma vertical da EC50.
d <- c(0, 0.01, 1, 10, 100, 1000)
scales <- list(x = list(at = d^k, labels = d))
ggplot(data = db,
mapping = aes(x = x, y = g100m, color = fung)) +
facet_wrap(facets = ~isol) +
geom_point() +
geom_line(data = pdto,
inherit.aes = FALSE,
mapping = aes(x = x, y = fit, color = fung))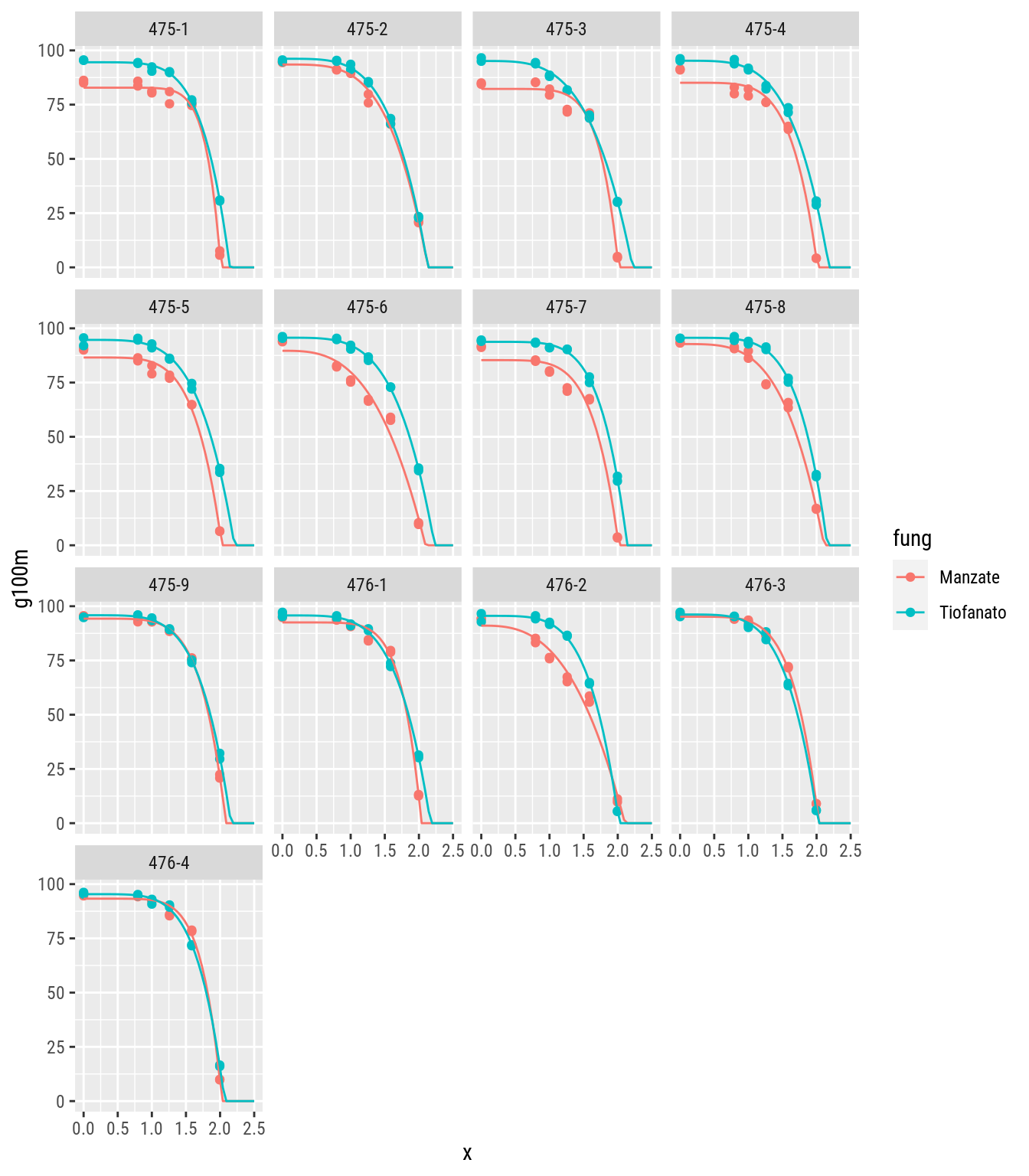
#----------------------------------------------------------------------
# Tabela com os valores das estimativas e R2.
tb_r2 <- map_dbl(n00,
~1 - deviance(.)/deviance(lm(fitted(.) + residuals(.) ~ 1))) %>%
enframe(name = "caso", value = "R2") %>%
separate(col = "caso", into = c("fung", "isol"),
remove = FALSE, sep = "\\.")
tb_r2## # A tibble: 26 x 4
## caso fung isol R2
## <chr> <chr> <chr> <dbl>
## 1 Manzate.475-1 Manzate 475-1 0.992
## 2 Manzate.475-2 Manzate 475-2 0.992
## 3 Manzate.475-3 Manzate 475-3 0.983
## 4 Manzate.475-4 Manzate 475-4 0.986
## 5 Manzate.475-5 Manzate 475-5 0.992
## 6 Manzate.475-6 Manzate 475-6 0.973
## 7 Manzate.475-7 Manzate 475-7 0.976
## 8 Manzate.475-8 Manzate 475-8 0.989
## 9 Manzate.475-9 Manzate 475-9 0.999
## 10 Manzate.476-1 Manzate 476-1 0.991
## # … with 16 more rows2 Curva de germinação
2.1 Ajuste do modelo
# Germinação em função da temperatura e período de molhamento.
germ_m <- data.frame(molha = c(6, 12, 24, 6, 12, 24, 6, 12, 24, 6, 12,
24, 6, 12, 24, 6, 12, 24, 6, 12, 24, 6,
12, 24, 6, 12, 24),
tempe = c(15, 15, 15, 18, 18, 18, 20, 20, 20, 22,
22, 22, 25, 25, 25, 26, 26, 26, 28, 28,
28, 30, 30, 30, 32, 32, 32),
germ = c(0, 0, 0, 0.018, 0.015, 0.015, 0.028, 0.04,
0.05, 0.053, 0.1, 0.058, 0.068, 0.057,
0.073, 0.095, 0.133, 0.148, 0.038, 0.078,
0.17, 0.025, 0.038, 0.062, 0, 0, 0))
# Temperaturas fixadas para além do intervalo observado. Sem fixar não
# tem como estimar os 5 parâmetros.
tmin <- 14.9
tmax <- 32.1
tran <- tmax - tmin
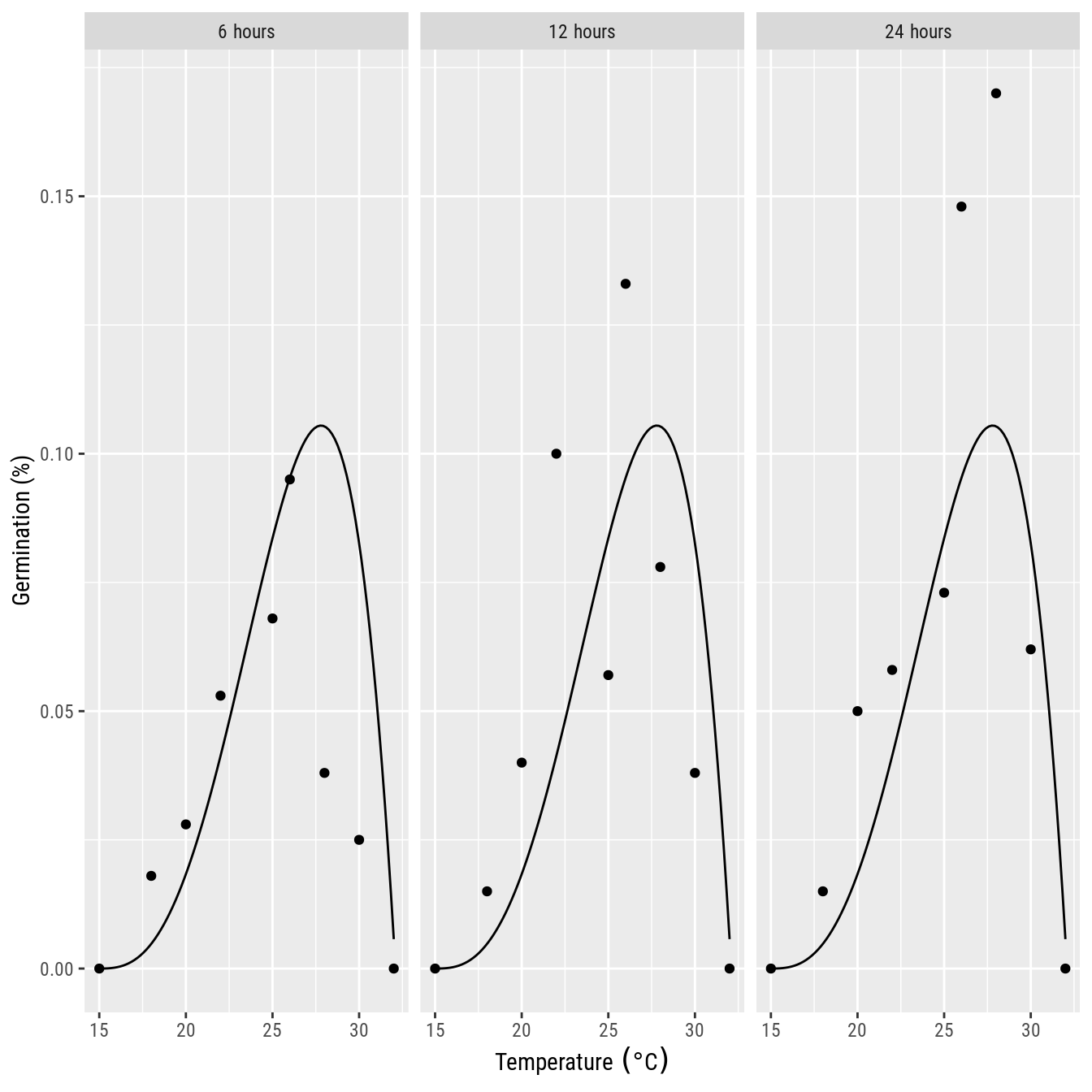
ggplot(data = germ_m,
mapping = aes(tempe, germ)) +
facet_wrap(facets = ~molha,
labeller = label_bquote(.(molha) ~ "hours")) +
geom_point() +
labs(x = expression("Temperature" ~ (degree * C)),
y = "Germination (%)") +
geom_function(fun = function(tempe, A = 1, B = 3, C = 1) {
A * ((tempe - tmin)/tran)^B * ((tmax - tempe)/tran)^C
})
# Ajuste do modelo aos dados.
n00 <- nlsList(germ ~ A * ((tempe - tmin)/tran)^B * ((tmax - tempe)/tran)^C | molha,
data = germ_m,
start = list(A = 1, B = 3, C = 1))
coef(n00)## A B C
## 6 2.840363 3.113921 2.195154
## 12 1.294726 2.273736 1.515047
## 24 4.362685 4.074284 1.630117# Valores preditos para sobrepor.
pred <- with(germ_m,
crossing(molha = unique(molha),
tempe = seq(min(tempe),
max(tempe),
length.out = 43)))
pred$fit <- predict(n00, newdata = pred)
# Confere os ajustes.
ggplot(data = germ_m,
mapping = aes(tempe, germ)) +
facet_wrap(facets = ~molha,
ncol = 1,
labeller = label_bquote(.(molha) ~ "hours")) +
geom_point() +
labs(x = expression("Temperature" ~ (degree * C)),
y = "Germination (%)") +
geom_line(data = pred,
mapping = aes(x = tempe, y = fit))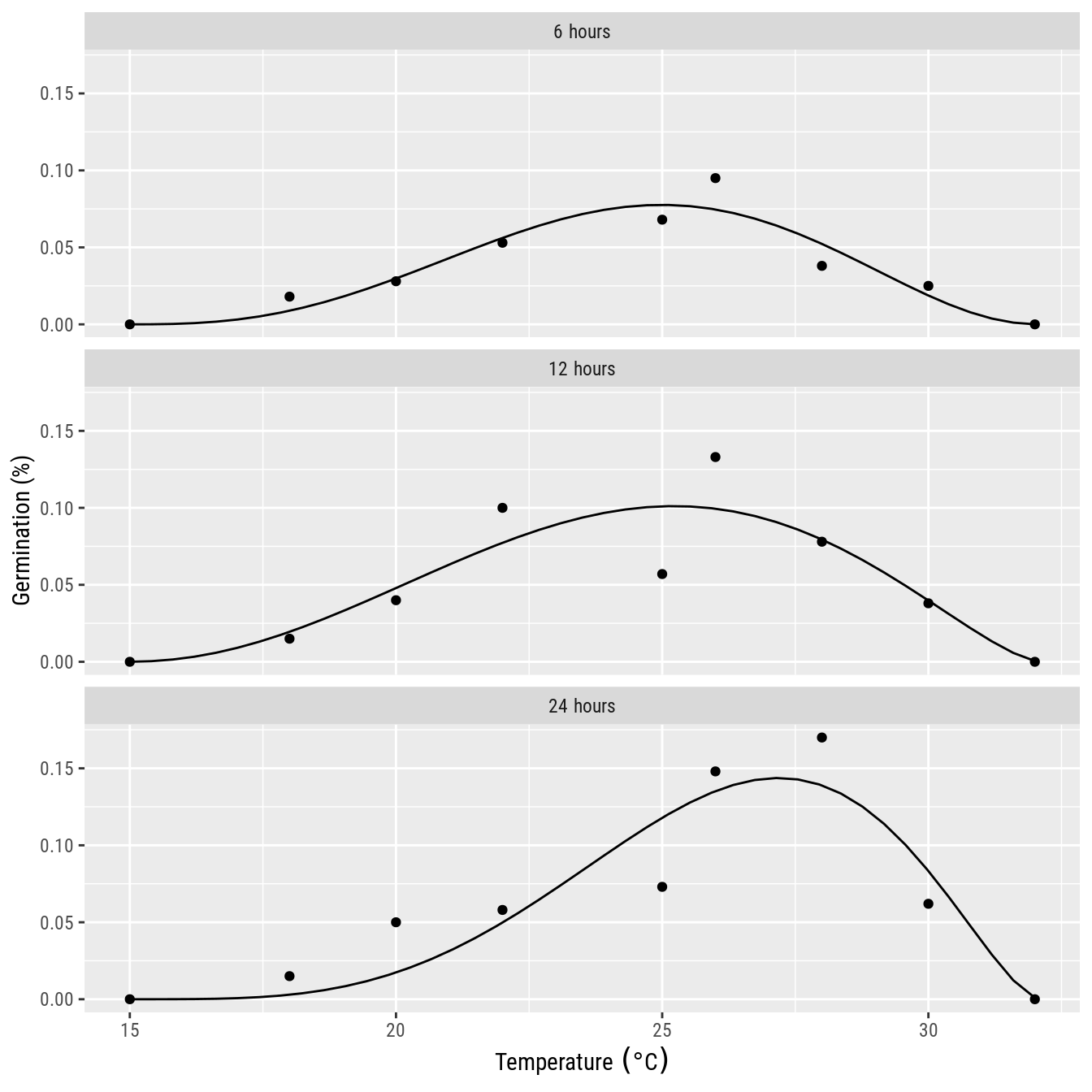
2.2 Pontos críticos
# No www.wolframalpha.com, fazer as operações.
# 1. Obter a derivada: derivative of x^b*(1-x)^c wrt x
# 2. Resolver: solve b * (1 - x)^c * x^(-1 + b) - c * (1 - x)^(-1 + c) * x^b = 0
# Por comodidade, acesse os links.
# browseURL("https://www.wolframalpha.com/input/?i=derivative+of+x%5Eb*%281-x%29%5Ec+wrt+x")
# browseURL("https://www.wolframalpha.com/input/?i=solve+b+*+%281+-+x%29%5Ec+*+x%5E%28-1+%2B+b%29+-+c+*+%281+-+x%29%5E%28-1+%2B+c%29+*+x%5Eb+%3D+0")
# Temperatura para germinação máxima (método delta).
g_fun <- sprintf("(B)/(B + C) * (%0.2f) + %0.2f",
tran,
tmin)
# Intervalo de confiança pelo método delta.
dm <- map(n00, deltaMethod, g = g_fun)
temp_dm <- cbind(molha = as.numeric(names(dm)),
do.call(rbind, dm))
temp_dm## molha Estimate SE 2.5 % 97.5 %
## 6 6 24.98828 0.4949410 24.01821 25.95835
## 12 12 25.22212 0.8874853 23.48268 26.96156
## 24 24 27.18485 0.6172546 25.97505 28.39464# Germinação da temperatura de ótimo (método delta).
topt <- temp_dm$Estimate
h_fun <- sprintf("A * ((%f - %f)/%f)^B * ((%f - %f)/%f)^C",
topt,
tmin,
tmax - tmin,
tmax,
topt,
tmax - tmin)
# Intervalo de confiança pelo método delta.
dm <- map2(n00, h_fun, deltaMethod)
germ_dm <- cbind(molha = as.numeric(names(dm)), do.call(rbind, dm))
germ_dm## molha Estimate SE 2.5 % 97.5 %
## 6 6 0.07760384 0.008085734 0.06175609 0.09345159
## 12 12 0.10112406 0.015788584 0.07017900 0.13206911
## 24 24 0.14371181 0.020037947 0.10443815 0.18298546# Gráfico final.
ggplot(data = germ_m,
mapping = aes(tempe, germ)) +
facet_wrap(facets = ~molha,
labeller = label_bquote(.(molha) ~ "hours")) +
geom_point() +
labs(x = expression("Temperature" ~ (degree * C)),
y = "Germination (%)") +
geom_line(data = pred,
mapping = aes(x = tempe, y = fit)) +
geom_vline(data = temp_dm,
mapping = aes(xintercept = Estimate),
color = "orange", lty = 2) +
geom_hline(data = germ_dm,
mapping = aes(yintercept = Estimate),
color = "orange", lty = 2)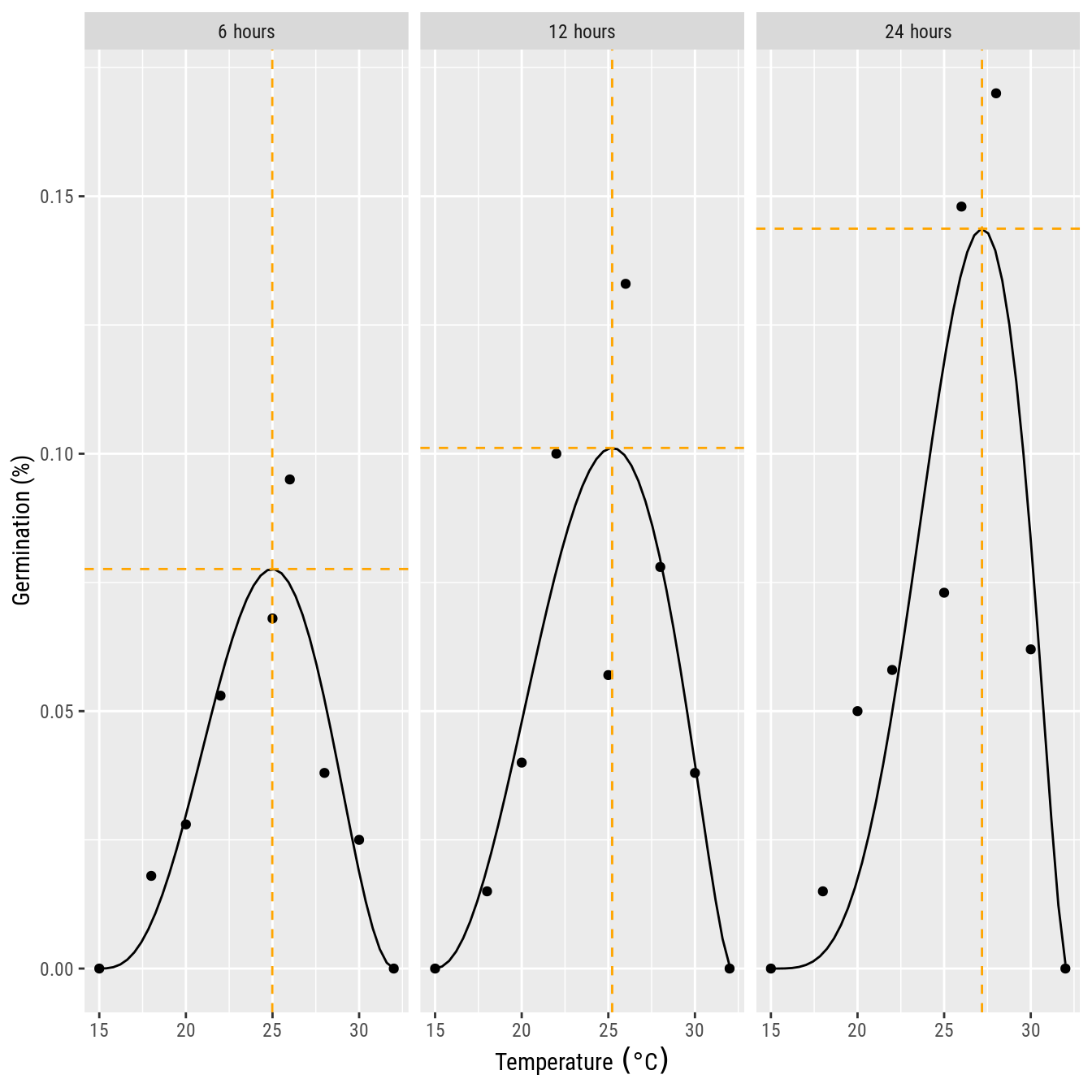
|
Modelos de Regressão Não Linear: Fundamentos e Aplicações em R leg.ufpr.br/~walmes/cursoR/mrnl |
Prof. Walmes M. Zeviani Departamento de Estatística · UFPR |
