Existem várias formas de resumir a informação descrita na distribuição a posteriori. Esta etapa frequentemente envolve a avaliação de probabilidades ou esperanças.
Neste capítulo serão descritos métodos baseados em simulação, incluindo Monte Carlo simples, Monte Carlo com função de importância, o método do Bootstrap Bayesiano e Monte Carlo via cadeias de Markov (MCMC). O material apresentado é introdutório e mais detalhes sobre os estes métodos podem ser obtidos em Gamerman (1997), Davison e Hinckley (1997) e Robert e Casella (1999). Outros métodos computacionalmente intensivos como técnicas de otimização e integração numérica, bem como aproximações analíticas não serão tratados aqui e uma referência introdutória é Migon e Gamerman (1999).
Todos os algoritmos que serão vistos aqui são não determinísticos, i.e. todos requerem a simulação de números (pseudo) aleatórios de alguma distribuição de probabilidades. Em geral, a única limitação para o número de simulações são o tempo de computação e a capacidade de armazenamento dos valores simulados. Assim, se houver qualquer suspeita de que o número de simulações é insuficiente, a abordagem mais simples consiste em simular mais valores.
Apesar da sua grande utilidade, os métodos que serão apresentados aqui devem ser aplicados com cautela. Devido à facilidade com que os recursos computacionais podem ser utilizados hoje em dia, corremos o risco de apresentar uma solução para o problema errado (o erro tipo 3) ou uma solução ruim para o problema certo. Assim, os métodos computacionalmente intensivos não devem ser vistos como substitutos do pensamento crítico sobre o problema por parte do pesquisador.
Além disso, sempre que possível deve-se utilizar soluções exatas, i.e. não aproximadas, se elas existirem. Por exemplo, em muitas situações em que precisamos calcular uma integral múltipla existe solução exata em algumas dimensões, enquanto nas outras dimensões temos que usar métodos de aproximação.
A distribuição a posteriori pode ser convenientemente resumida
em termos de esperanças de funções particulares
do parâmetro ![]() , i.e.
, i.e.
![$\displaystyle E[g(\theta)\vert\bfx]=\int g(\theta) p(\theta\vert\bfx) d\theta
$](img551.png)
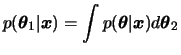
Assim, o problema geral da inferência Bayesiana consiste em calcular
tais valores esperados segundo a distribuição a posteriori de
![]() . Alguns exemplos são,
. Alguns exemplos são,
![$\displaystyle k=\left[\int q(\theta) d\theta\right]^{-1}.$](img557.png)
Portanto, a habilidade de integrar funções, muitas vezes complexas e multidimensionais, é extremamente importante em inferência Bayesiana. Inferência exata somente será possível se estas integrais puderem ser calculadas analiticamente, caso contrário devemos usar aproximações. Nas próximas seções iremos apresentar métodos aproximados baseados em simulação para obtenção dessas integrais.
A idéia do método é justamente escrever a integral que se deseja
calcular como um valor esperado. Para introduzir o método considere o
problema de calcular a integral de uma função ![]() no intervalo
no intervalo
![]() , i.e.
, i.e.
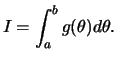
Esta integral pode ser reescrita como
![$\displaystyle I=\int_a^b (b-a)g(\theta)\frac{1}{b-a}d\theta = (b-a)E[g(\theta)]
$](img572.png)
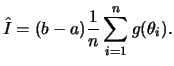
Não é difícil verificar que esta estimativa é não viesada já que
![$\displaystyle E(\hat{I})=\frac{(b-a)}{n}\sum_{i=1}^n E[g(\theta_i)]=
(b-a)E[g(\theta)]=\int_a^b g(\theta)d\theta.
$](img578.png)
Podemos então usar o seguinte algoritmo
A generalização é bem simples para o caso em que a integral é a
esperança matemática de uma função ![]() onde
onde ![]() tem função de
densidade
tem função de
densidade ![]() , i.e.
, i.e.
Uma vez que as gerações são independentes, pela Lei Forte dos Grandes
Números segue que ![]() converge quase certamente para
converge quase certamente para ![]() . Além
disso, a variância do estimador pode também ser estimada como
. Além
disso, a variância do estimador pode também ser estimada como
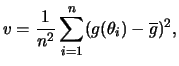
Para ![]() grande segue que
grande segue que
![$\displaystyle \frac{\overline{g}-E[g(\theta)]}{\sqrt{v}}
$](img586.png)
No caso multivariado a extensão também é direta. Seja
![]() um vetor aleatório de dimensão
um vetor aleatório de dimensão ![]() com função de
densidade
com função de
densidade
![]() . Neste caso os valores gerados serão também
vetores
. Neste caso os valores gerados serão também
vetores
![]() e o estimador de Monte Carlo fica
e o estimador de Monte Carlo fica
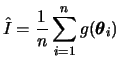
Em muitas situações pode ser muito custoso ou mesmo impossível simular
valores da distribuição a posteriori. Neste caso, pode-se
recorrer à uma função ![]() que seja de fácil amostragem, usualmente
chamada de função de importância. O procedimento é comumente
chamado de amostragem por importância.
que seja de fácil amostragem, usualmente
chamada de função de importância. O procedimento é comumente
chamado de amostragem por importância.
Se ![]() for uma função de densidade definida no mesmo espaço
variação de
for uma função de densidade definida no mesmo espaço
variação de ![]() então a integral (4.1) pode ser reescrita
como
então a integral (4.1) pode ser reescrita
como
![$\displaystyle I=\int\frac{g(\theta)p(\theta)}{q(\theta)}q(\theta)dx =
E\left[\frac{g(\theta)p(\theta)}{q(\theta)}\right]
$](img593.png)
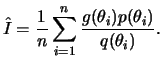
Em princípio não há restrições quanto à escolha da densidade de
importância ![]() , porém na prática alguns cuidados devem ser
tomados. Pode-se mostrar que a escolha ótima no sentido de minimizar a
variância do estimador consiste em tomar
, porém na prática alguns cuidados devem ser
tomados. Pode-se mostrar que a escolha ótima no sentido de minimizar a
variância do estimador consiste em tomar
![]() .
.
Para uma única observação ![]() com
distribuição
com
distribuição
![]() ,
,
![]() desconhecido, e priori Cauchy(0,1) segue que
desconhecido, e priori Cauchy(0,1) segue que
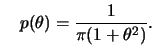
![$\displaystyle p(\theta\vert x)=
\frac{\dfrac{1}{1+\theta^2}\exp[-(x-\theta)^2/2]}
{\dint\dfrac{1}{1+\theta^2}\exp[-(x-\theta)^2/2]d\theta}.
$](img600.png)
![$\displaystyle E[\theta\vert\bfx] = \int\theta p(\theta\vert\bfx)d\theta=\frac
{...
...\theta)^2/2]d\theta}
{\dint\dfrac{1 }{1+\theta^2}\exp[-(x-\theta)^2/2]d\theta}
$](img601.png)
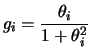 e
e
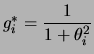 ;
;
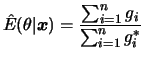 .
.
Este exemplo ilustrou um problema que geralmente ocorre em aplicações Bayesianas. Como a posteriori só é conhecida a menos de uma constante de proporcionalidade as esperanças a posteriori são na verdade uma razão de integrais. Neste caso, a aproximação é baseada na razão dos dois estimadores de Monte Carlo para o numerador e denominador.
Existem distribuições para as quais é muito difícil ou mesmo impossível simular valores. A idéia dos métodos de reamostragem é gerar valores em duas etapas. Na primeira etapa gera-se valores de uma distribuição auxiliar conhecida. Na segunda etapa utiliza-se um mecanismo de correção para que os valores sejam representativos (ao menos aproximadamente) da distribuição a posteriori. Na prática costuma-se tomar a priori como distribuição auxiliar conforme proposto em Smith e Gelfand (1992).
Considere uma densidade auxiliar ![]() da qual sabemos gerar
valores. A única restrição é que exista uma constante
da qual sabemos gerar
valores. A única restrição é que exista uma constante ![]() finita tal
que
finita tal
que
![]() .
O método de rejeição consiste em gerar um valor
.
O método de rejeição consiste em gerar um valor ![]() da
distribuição auxiliar
da
distribuição auxiliar ![]() e aceitar este valor como sendo da
distribuição a posteriori com probabilidade
e aceitar este valor como sendo da
distribuição a posteriori com probabilidade
![]() . Caso contrário,
. Caso contrário, ![]() não é aceito
como uma valor gerado da posteriori e o processo é repetido até que um
valor seja aceito. O método também funciona se ao invés da posteriori,
que em geral é desconhecida, usarmos a sua versão não normalizada, i.e
não é aceito
como uma valor gerado da posteriori e o processo é repetido até que um
valor seja aceito. O método também funciona se ao invés da posteriori,
que em geral é desconhecida, usarmos a sua versão não normalizada, i.e
![]() .
.
Tomando a priori ![]() como densidade auxiliar a constante
como densidade auxiliar a constante ![]() deve ser
tal que
deve ser
tal que
![]() . Esta desigualdade é satisfeita se tomarmos
. Esta desigualdade é satisfeita se tomarmos
![]() como sendo o valor máximo da função de verossimilhança,
i.e.
como sendo o valor máximo da função de verossimilhança,
i.e.
![]() onde
onde
![]() é o estimador de
máxima verossimilhança de
é o estimador de
máxima verossimilhança de ![]() . Neste caso, a probabilidade de
aceitação se simplifica para
. Neste caso, a probabilidade de
aceitação se simplifica para
![]() .
.
Podemos então usar o seguinte algoritmo para gerar valores da posteriori
Um problema técnico associado ao método é a necessidade de se maximizar a função de verossimilhança o que pode não ser uma tarefa simples em modelos mais complexos. Se este for o caso então o método de rejeição perde o seu principal atrativo que é a simplicidade. Neste caso, o método da próxima seção passa a ser recomendado.
Outro problema é que a taxa de aceitação pode ser muito baixa, i.e. teremos que gerar muitos valores da distribuição auxiliar até conseguir um número suficiente de valores da posteriori. Isto ocorrerá se as informações da priori e da verossimilhança forem conflitantes já que neste caso os valores gerados terão baixa probabilidade de serem aceitos.
Estes métodos usam a mesma idéia de gerar valores de uma distribuição auxiliar porém sem a necessidade de maximização da verossimilhança. A desvantagem é que os valores obtidos são apenas aproximadamente distribuidos segundo a posteriori.
Suponha que temos uma amostra
![]() gerada da
distribuição auxiliar
gerada da
distribuição auxiliar ![]() e a partir dela construimos os pesos
e a partir dela construimos os pesos
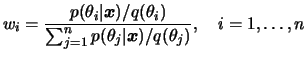
Tomando novamente a priori como densidade auxiliar,
i.e.
![]() os pesos se simplificam para
os pesos se simplificam para
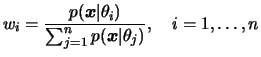
function()
{
# Obtem uma amostra da distribuicao a posteriori dos parametros em um
# modelo de regressao linear simples via metodo de reamostragem
# ponderada (Exercicio 1, desta seção);
x <- c(-2,-1,0,1,2)
y <- c(-2, 0,0,0,2)
n <- 1000; \# tamanho da amostra da priori
m <- 500 ; \# tamanho da reamostra
par(mfrow = c(2, 2))
beta <- matrix(rnorm(n, 0, 2), nrow = n)
l <- matrix(NA, nrow = n)
for(i in 1:n){
l[i] <- exp(- (1/2) * t(y - beta[i] * x) %*% (y - beta[i] * x))
}
p <- matrix(NA, nrow = n)\\
for(i in 1:n)
{
p[i] <- l[i]/sum(l)
}
resample <- sample(beta, size = m, replace = T, prob = p)
hist(beta, col = 0, prob = T, title="priori")
plot(beta, l, title="")
hist(resample, col = 0, prob = T)
list(beta = summary(beta), resample = summary(resample))
}
Em todos os métodos de simulação vistos até agora obtém-se uma amostra da distribuição a posteriori em um único passo. Os valores são gerados de forma independente e não há preocupação com a convergência do algoritmo, bastando que o tamanho da amostra seja suficientemente grande. Por isso estes métodos são chamados não iterativos (não confundir iteração com interação). No entanto, em muitos problemas pode ser bastante difícil, ou mesmo impossível, encontrar uma densidade de importância que seja simultaneamente uma boa aproximação da posteriori e fácil de ser amostrada.
Os métodos de Monte Carlo via cadeias de Markov (MCMC) são uma alternativa aos métodos não iterativos em problemas complexos. A idéia ainda é obter uma amostra da distribuição a posteriori e calcular estimativas amostrais de características desta distribuição. A diferença é que aqui usaremos técnicas de simulação iterativa, baseadas em cadeias de Markov, e assim os valores gerados não serão mais independentes.
Neste capítulo serão apresentados os métodos MCMC mais utilizados,
o amostrador de Gibbs e o algoritmo de Metropolis-Hastings. A idéia
básica é simular um passeio aleatório no espaço de ![]() que converge
para uma distribuição estacionária, que é a distribuição
de interesse no problema. Uma discussão mais geral sobre o tema pode
ser encontrada por exemplo em gam97.
que converge
para uma distribuição estacionária, que é a distribuição
de interesse no problema. Uma discussão mais geral sobre o tema pode
ser encontrada por exemplo em gam97.
Uma cadeia de Markov é um processo estocástico
![]() tal que a distribuição de
tal que a distribuição de ![]() dados todos os valores anteriores
dados todos os valores anteriores
![]() depende apenas de
depende apenas de ![]() . Matematicamente,
. Matematicamente,
Os algoritmos de Metropolis-Hastings usam a mesma idéia dos métodos de rejeição vistos no capítulo anterior, i.e. um valor é gerado de uma distribuição auxiliar e aceito com uma dada probabilidade. Este mecanismo de correção garante que a convergência da cadeia para a distribuição de equilibrio, que neste caso é a distribuição a posteriori.
Suponha que a cadeia esteja no estado ![]() e um valor
e um valor ![]() é
gerado de uma distribuição proposta
é
gerado de uma distribuição proposta
![]() . Note que
a distribuição proposta pode depender do estado atual da cadeia, por
exemplo
. Note que
a distribuição proposta pode depender do estado atual da cadeia, por
exemplo
![]() poderia ser uma distribuição normal centrada
em
poderia ser uma distribuição normal centrada
em ![]() . O novo valor
. O novo valor ![]() é aceito com probabilidade
é aceito com probabilidade
Uma característica importante é que só precisamos conhecer ![]() parcialmente, i.e. a menos de uma constante já que neste caso a
probabilidade (4.2) não se altera. Isto é fundamental em
aplicações Bayesianas aonde não conhecemos completamente a posteriori.
parcialmente, i.e. a menos de uma constante já que neste caso a
probabilidade (4.2) não se altera. Isto é fundamental em
aplicações Bayesianas aonde não conhecemos completamente a posteriori.
Em termos práticos, o algoritmo de Metropolis-Hastings pode ser especificado pelos seguintes passos,
Uma useful feature of the algorithm is that the target distribution needs only be known up to a constant of proportionality since only the target ratio
![]() is used in the acceptance probability. Note also that the chain may remain in the same state for many iterations and in practice a useful monitoring device is given by the average percentage of iterations for which moves are accepted. Hastings (1970) suggests that this acceptance rate should always be computed in practical applications.
is used in the acceptance probability. Note also that the chain may remain in the same state for many iterations and in practice a useful monitoring device is given by the average percentage of iterations for which moves are accepted. Hastings (1970) suggests that this acceptance rate should always be computed in practical applications.
The independence sampler is a Metropolis-Hastings algorithm whose proposal distribution does not depend on the current state of the chain, i.e.,
![]() . In general,
. In general, ![]() should be a good approximation of
should be a good approximation of
![]() , but it is safest if
, but it is safest if ![]() is heavier-tailed than
is heavier-tailed than
![]() .
.
The Metropolis algorithm considers only symmetric proposals, i.e.,
![]() for all values of
for all values of ![]() and
and ![]() , and the acceptance probability reduces to
, and the acceptance probability reduces to
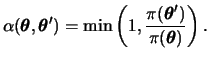
A special important case is the random-walk Metropolis for which
![]() , so that the probability of generating a move from
, so that the probability of generating a move from ![]() to
to ![]() depends only on the distance between them. Using a proposal distribution with variance
depends only on the distance between them. Using a proposal distribution with variance ![]() , very small values of
, very small values of ![]() will lead to small jumps which are almost all accepted but it will be difficult to traverse the whole parameter space and it will take many iterations to converge. On the other hand, large values of
will lead to small jumps which are almost all accepted but it will be difficult to traverse the whole parameter space and it will take many iterations to converge. On the other hand, large values of ![]() will lead to an excessively high rejection rate since the proposed values are likely to fall in the tails of the posterior distribution.
will lead to an excessively high rejection rate since the proposed values are likely to fall in the tails of the posterior distribution.
Typically, there will be an optimal value for the proposal scale ![]() determined on the basis of a few pilot runs which lies in between these two extremes (see for example, Roberts, Gelman and Gilks, 1997). We return to this point later and, in particular, discuss an approach for choosing optimal values for the parameters of the proposal distribution for
(RJ)MCMC algorithms in Chapter 6.
determined on the basis of a few pilot runs which lies in between these two extremes (see for example, Roberts, Gelman and Gilks, 1997). We return to this point later and, in particular, discuss an approach for choosing optimal values for the parameters of the proposal distribution for
(RJ)MCMC algorithms in Chapter 6.
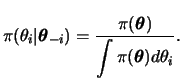
If generation schemes to draw a sample directly from
![]() are costly, complicated or simply unavailable but the full conditional distributions are completely known and can be sampled from, then Gibbs sampling proceeds as follows,
are costly, complicated or simply unavailable but the full conditional distributions are completely known and can be sampled from, then Gibbs sampling proceeds as follows,
However, the Gibbs sampler does not apply to problems where the number of parameters varies because of the lack of irreducibility of the resulting chain. When the length of ![]() is not fixed and its elements need not have a fixed interpretation across all models, to resample some components conditional on the remainder would rarely be meaninful.
is not fixed and its elements need not have a fixed interpretation across all models, to resample some components conditional on the remainder would rarely be meaninful.
Note also that the Gibbs sampler is a special case of the Metropolis-Hastings algorithm, in which individual elements of ![]() are updated one at a time (or in blocks), with the full conditional distribution as the candidate generating function and acceptance probabilities uniformly equal to 1.
are updated one at a time (or in blocks), with the full conditional distribution as the candidate generating function and acceptance probabilities uniformly equal to 1.
In the above scheme, all the components of ![]() are updated in the same deterministic order at every iteration. However, other scanning or updating strategies are possible for visiting the components of
are updated in the same deterministic order at every iteration. However, other scanning or updating strategies are possible for visiting the components of ![]() . Geman and Geman (1984) showed in a discrete setting that any updating scheme that guarantees that all components are visited infinitely often when the chain is run indefinitely, converges to the joint distribution of interest, i.e.,
. Geman and Geman (1984) showed in a discrete setting that any updating scheme that guarantees that all components are visited infinitely often when the chain is run indefinitely, converges to the joint distribution of interest, i.e.,
![]() . For example, Zeger and Karim (1991) describe a Gibbs sampling scheme where some components are visited only every
. For example, Zeger and Karim (1991) describe a Gibbs sampling scheme where some components are visited only every ![]() th iteration, which still guarantees that every component is updated infinitely often for finite, fixed
th iteration, which still guarantees that every component is updated infinitely often for finite, fixed ![]() .
.
Roberts and Sahu (1997) consider a random permutation scan where at each iteration a permutation of
![]() is chosen and components are visited in that order. In particular, they showed that when
is chosen and components are visited in that order. In particular, they showed that when
![]() is multivariate normal, convergence for the deterministic scan is faster than for the random scan if the precision matrix is tridiagonal (
is multivariate normal, convergence for the deterministic scan is faster than for the random scan if the precision matrix is tridiagonal (![]() depends only on
depends only on
![]() and
and
![]() ) or if it has non-negative partial correlations.
) or if it has non-negative partial correlations.
In principle, the way the components of the parameter vector ![]() are arranged in blocks of parameters is completely arbitrary and includes blocks formed by scalar components as special cases. However, the structure of the Gibbs sampler imposes moves according to the coordinate axes of the blocks, so that larger blocks allow moves in more general directions. This can be very beneficial, although more computationally demanding, in a context where there is high correlation between individual components since these higher dimensional moves incorporate information about this dependence. Parameter values are then generated from the joint full conditional distribution for the block of parameters considered.
are arranged in blocks of parameters is completely arbitrary and includes blocks formed by scalar components as special cases. However, the structure of the Gibbs sampler imposes moves according to the coordinate axes of the blocks, so that larger blocks allow moves in more general directions. This can be very beneficial, although more computationally demanding, in a context where there is high correlation between individual components since these higher dimensional moves incorporate information about this dependence. Parameter values are then generated from the joint full conditional distribution for the block of parameters considered.
Roberts and Sahu (1997) showed that for a multivariate normal ![]() and random scans, convergence improves as the number of blocks decreases. They also proved that blocking can hasten convergence for non-negative partial correlation distributions and even more as the partial correlation of the components in the block gets larger. However, they also provided an example where blocking worsens convergence.
and random scans, convergence improves as the number of blocks decreases. They also proved that blocking can hasten convergence for non-negative partial correlation distributions and even more as the partial correlation of the components in the block gets larger. However, they also provided an example where blocking worsens convergence.
Even when every full conditional distribution associated with the target distribution ![]() is not explicit there can be a density
is not explicit there can be a density ![]() for which
for which ![]() is a marginal density, i.e.,
is a marginal density, i.e.,
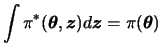
This approach was actually one of the first appearances of the Gibbs sampler in Statistics with the introduction of data augmentation by Tanner and Wong (1987). It is also worth noting that, in principle, this Gibbs sampler does not require that the completion of ![]() into
into ![]() and of
and of ![]() into
into
![]() should be related to the problem of interest and the vector
should be related to the problem of interest and the vector ![]() might have no meaning from a statistical point of view.
might have no meaning from a statistical point of view.
This is a very general version of the Gibbs sampler which applies to most distributions and is based on the simulation of specific uniform random variables. In its simplest version when only one variable is being updated, if ![]() can be written as a product of functions, i.e.,
can be written as a product of functions, i.e.,
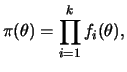
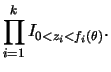
The slice sampler consists of generating
![]() from their full conditional distributions, i.e.,
from their full conditional distributions, i.e.,
Roberts and Rosenthal (1998) study the slice sampler and show that it usually enjoys good theoretical properties. In practice there may be problems as
![]() increases since the determination of the set
increases since the determination of the set ![]() may get increasingly complex.
may get increasingly complex.
Further details about the Gibbs sampler and related algorithms are given, for example, in Gamerman (1997, Chapter 5) and Robert and Casella (1999, Chapter 7).
The posterior model probability is obtained as
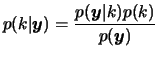
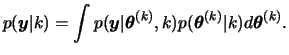
Hence, the posterior probability of a certain model is proportional to the product of the prior probability and the marginal likelihood for that model. It is also worth noting that, in practice, ![]() is unknown so that typically the model probabilities are known only up to a normalisation constant.
is unknown so that typically the model probabilities are known only up to a normalisation constant.
The above integral is commonly analytically intractable but may be approximated in a number of ways by observing that it can be regarded as the expected value of the likelihood with respect to the prior distribution
![]() . In terms of simulation techniques, the simplest estimate consists of simulating
. In terms of simulation techniques, the simplest estimate consists of simulating ![]() values
values
![]() from the prior, evaluating the likelihood at those values and computing the Monte Carlo estimate
from the prior, evaluating the likelihood at those values and computing the Monte Carlo estimate
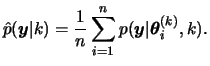
Having obtained the posterior model probabilities these may be used for either selecting the model with the highest probability or highest Bayes factor from the list of candidate models (model selection), or estimating some quantity under each model and then averaging the estimates according to how likely each model is, that is, using these probabilities as weights (model averaging). In the next section, we present MCMC methods that take into account different models simultaneously.