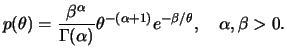


Next: A. Lista de Distribuições
Up: Introdução a Inferência Bayesiana
Previous: 4. Computação Bayesiana
Sumário
Subsections
- No exemplo dos físicos nas notas de aula, obtenha também a
distribuição preditiva de
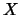 e compare o valor observado com a
média desta preditiva para os 2 físicos. Faça uma previsão
para uma
e compare o valor observado com a
média desta preditiva para os 2 físicos. Faça uma previsão
para uma
 medição
medição 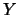 feita com o mesmo aparelho.
feita com o mesmo aparelho.
- Uma máquina produz
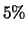 de itens defeituosos. Cada item produzido passa por um teste de qualidade
que o classifica como `` bom '', `` defeituoso '' ou `` suspeito ''. Este teste
classifica
de itens defeituosos. Cada item produzido passa por um teste de qualidade
que o classifica como `` bom '', `` defeituoso '' ou `` suspeito ''. Este teste
classifica 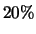 dos itens defeituosos como bons e
dos itens defeituosos como bons e 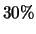 como suspeitos. Ele também classifica
como suspeitos. Ele também classifica 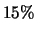 dos itens bons como defeituosos e
dos itens bons como defeituosos e 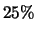 como suspeitos.
(a) Que proporção dos itens serão classificados como suspeitos ?
(b) Qual a probabilidade de um item classificado como suspeito ser defeituoso ?
(c) Outro teste, que classifica
como suspeitos.
(a) Que proporção dos itens serão classificados como suspeitos ?
(b) Qual a probabilidade de um item classificado como suspeito ser defeituoso ?
(c) Outro teste, que classifica 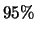 dos itens defeituosos e
dos itens defeituosos e 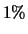 dos itens bons como defeituosos,
é aplicado somente aos itens suspeitos.
(d) Que proporção de itens terão a suspeita de defeito confirmada ?
(e) Qual a probabilidade de um item reprovado neste
dos itens bons como defeituosos,
é aplicado somente aos itens suspeitos.
(d) Que proporção de itens terão a suspeita de defeito confirmada ?
(e) Qual a probabilidade de um item reprovado neste
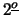 teste ser defeituoso ?
teste ser defeituoso ?
- Mostre que a família de distribuições Beta é conjugada em
relação às distribuições amostrais binomial, geométrica e binomial
negativa.
- Para uma amostra aleatória de 100 observações da distribuição
normal com média
 e desvio-padrão 2 foi especificada uma
priori normal para
e desvio-padrão 2 foi especificada uma
priori normal para  .
.
- Mostre que o desvio-padrão a posteriori será sempre menor do
que 1/5. Interprete este resultado.
- Se o desvio-padrão a priori for igual a 1 qual deve ser o
menor número de observações para que o desvio-padrão a posteriori
seja 0,1?
- Seja
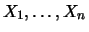 uma amostra aleatória da distribuição
uma amostra aleatória da distribuição
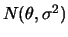 , com
, com  conhecido. Utilizando uma distribuição
a priori Gama para
conhecido. Utilizando uma distribuição
a priori Gama para 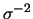 com coeficiente de variação 0,5, qual
deve ser o tamanho amostral para que o coeficiente de variação a
posteriori diminua para 0,1?
com coeficiente de variação 0,5, qual
deve ser o tamanho amostral para que o coeficiente de variação a
posteriori diminua para 0,1?
- Seja
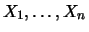 uma amostra aleatória da distribuição
uma amostra aleatória da distribuição
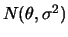 , com
, com  e
e 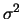 desconhecidos, e considere a
priori conjugada de
desconhecidos, e considere a
priori conjugada de
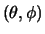 .
.
- Determine os parâmetros
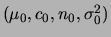 utilizando as seguintes informações a priori:
utilizando as seguintes informações a priori:
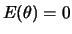 ,
,
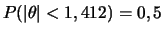 ,
, 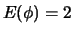 e
e
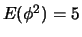 .
.
- Em uma amostra de tamanho
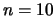 foi observado
foi observado
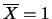 e
e
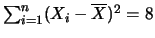 . Obtenha a
distribuição a posteriori de
. Obtenha a
distribuição a posteriori de  e esboce os gráficos das
distribuições a priori, a posteriori e da função de verossimilhança,
com
e esboce os gráficos das
distribuições a priori, a posteriori e da função de verossimilhança,
com 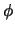 fixo.
fixo.
- Calcule
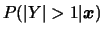 onde
onde 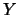 é uma observação tomada da
mesma população.
é uma observação tomada da
mesma população.
- Suponha que o tempo, em minutos, para atendimento a clientes
segue uma distribuição exponencial com parâmetro
 desconhecido. Com base na experiência anterior assume-se uma
distribuição a priori Gama com média 0,2 e desvio-padrão 1 para
desconhecido. Com base na experiência anterior assume-se uma
distribuição a priori Gama com média 0,2 e desvio-padrão 1 para
 .
.
- Se o tempo médio para atender uma amostra aleatória de 20
clientes foi de 3,8 minutos, qual a distribuição a posteriori de
 .
.
- Qual o menor número de clientes que precisam ser observados para
que o coeficiente de variação a posteriori se reduza para 0,1?
- Seja
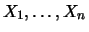 uma amostra aleatória da distribuição de
Poisson com parâmetro
uma amostra aleatória da distribuição de
Poisson com parâmetro  .
.
- Determine os parâmetros da priori conjugada de
 sabendo que
sabendo que
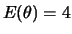 e o coeficiente de variação a priori é 0,5.
e o coeficiente de variação a priori é 0,5.
- Quantas observações devem ser tomadas até que a variância a
posteriori se reduza para 0,01 ou menos?
- Mostre que a média a posteriori é da forma
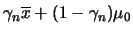 , onde
, onde
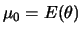 e
e
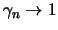 quando
quando
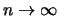 . Interprete este
resultado.
. Interprete este
resultado.
- O número médio de defeitos por 100 metros de uma fita magnética
é desconhecido e denotado por
 . Atribui-se uma distribuição
a priori Gama(2,10) para
. Atribui-se uma distribuição
a priori Gama(2,10) para  . Se um rolo de 1200 metros
desta fita foi inspecionado e encontrou-se 4 defeitos qual a
distribuição a posteriori de
. Se um rolo de 1200 metros
desta fita foi inspecionado e encontrou-se 4 defeitos qual a
distribuição a posteriori de  ?
?
- Seja
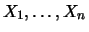 uma amostra aleatória da distribuição
Bernoulli com parâmetro
uma amostra aleatória da distribuição
Bernoulli com parâmetro  e usamos a priori conjugada
e usamos a priori conjugada
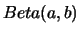 . Mostre que a média a posteriori é da forma
. Mostre que a média a posteriori é da forma
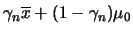 , onde
, onde
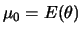 e
e
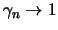 quando
quando
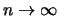 . Interprete
este resultado.
. Interprete
este resultado.
- Para uma amostra aleatória
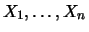 tomada da
distribuição
tomada da
distribuição
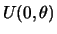 , mostre que a família de distribuições de
Pareto com parâmetros
, mostre que a família de distribuições de
Pareto com parâmetros 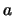 e
e 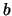 , cuja função de densidade é
, cuja função de densidade é
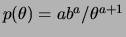 , é conjugada à uniforme.
, é conjugada à uniforme.
- Para uma variável aleatória
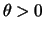 a família de
distribuições Gama-invertida tem função de densidade de
probabilidade dada por
Mostre que esta família é conjugada ao modelo normal com média
a família de
distribuições Gama-invertida tem função de densidade de
probabilidade dada por
Mostre que esta família é conjugada ao modelo normal com média 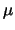 conhecida e variância
conhecida e variância  desconhecida.
desconhecida.
- Suponha que
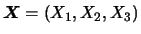 tenha distribuição trinomial
com parâmetros
tenha distribuição trinomial
com parâmetros 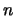 (conhecido) e
(conhecido) e
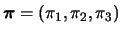 com
com
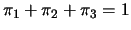 . Mostre que a priori não informativa de
Jeffreys para
. Mostre que a priori não informativa de
Jeffreys para 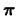 é
é
![$ p(\bfpi)\propto
[\pi_1\pi_2(1-\pi_1-\pi_2)]^{-1/2}$](img361.png) .
.
- Para cada uma das distribuições abaixo verifique se o modelo é
de locação, escala ou locação-escala e obtenha a priori não
informativa para os parâmetros desconhecidos.
- Cauchy(0,
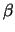 ).
).
-
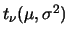 ,
, 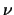 conhecido.
conhecido.
- Pareto(
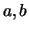 ),
), 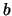 conhecido.
conhecido.
- Uniforme
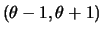 .
.
- Uniforme
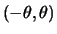 .
.
- Seja uma coleção de variáveis aleatórias
independentes
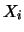 com distribuições
com distribuições
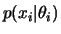 e seja
e seja
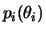 a priori não informativa de
a priori não informativa de 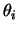 ,
,
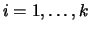 . Mostre que a priori não informativa de Jeffreys para
o vetor paramétrico
. Mostre que a priori não informativa de Jeffreys para
o vetor paramétrico
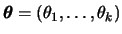 é dada por
é dada por
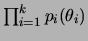 .
.
- Se
 tem priori não informativa
tem priori não informativa
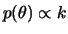 ,
,
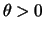 mostre que a priori de
mostre que a priori de
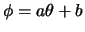 ,
, 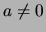 também é
também é
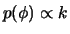 .
.
- Se
 tem priori não informativa
tem priori não informativa
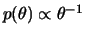 mostre que a priori de
mostre que a priori de
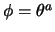 ,
, 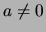 também é
também é
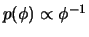 e que
a priori de
e que
a priori de
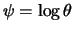 é
é
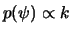 .
.
Resolva estes problemas usando o pacote estatístico R. Entregue os
resultados juntamente com os comandos que utilizou.
- Ensaios de Bernoulli.
- Gere uma amostra aleatória de tamanho 10 da distribuição de
Bernoulli com probabilidade de sucesso
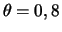
- Faça um gráfico com as funções de densidade das prioris
conjugadas Beta(6,2), Beta(2,6), Beta(1,1).
- Repita o gráfico anterior acrescentando a função de
verossimilhança. Note que a verossimilhança deve ser normalizada.
- Faça um gráfico com as funções de densidade das posterioris
usando as prioris acima e mais a priori nâo informativa de
Jeffreys. O que você conclui?
- Repita o item anterior com uma amostra de tamanho 100. O que
você conclui?
- Modelo de Poisson.
- Gere uma amostra aleatória de tamanho 10 da distribuição de
Poisson com média
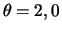
- Faça um gráfico com as funções de densidade das prioris
conjugadas Gama(5,2), Gama(2,5), Gama(1,1).
- Repita o gráfico anterior acrescentando a função de
verossimilhança. Note que a verossimilhança deve ser normalizada.
- Faça um gráfico com as funções de densidade das posterioris
usando as prioris acima e mais a priori nâo informativa de
Jeffreys. O que você conclui?
- Repita o item anterior com uma amostra de tamanho 100. O que
você conclui?
Resolva estes problemas usando o pacote estatístico R. Entregue os
resultados juntamente com os comandos que utilizou.
- Para uma única observação
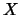 com
distribuição
com
distribuição
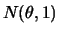 ,
,
 desconhecido, queremos fazer inferência sobre
desconhecido, queremos fazer inferência sobre  usando
uma priori Cauchy(0,1). Gere um valor de
usando
uma priori Cauchy(0,1). Gere um valor de 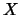 para
para 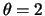 ,
i.e.
,
i.e.
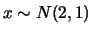 .
.
- Estime
 através da sua média a posteriori usando o
algoritmo do exemplo 4.1 das notas de aula.
através da sua média a posteriori usando o
algoritmo do exemplo 4.1 das notas de aula.
- Estime a variância da posteriori.
- Generalize o algoritmo para
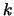 observações
observações
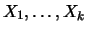 da
distribuição
da
distribuição
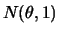 .
.
- Em um modelo de regressão linear simples temos que
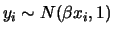 . Os dados observados são
. Os dados observados são
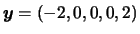 e
e
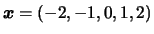 , e usamos uma priori vaga
, e usamos uma priori vaga 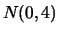 para
para
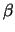 .
.
- Obtenha uma amostra da posteriori de
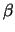 usando reamostragem
ponderada.
usando reamostragem
ponderada.
- Baseado nesta amostra, faça um histograma e estime
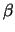 usando
uma aproximação para a média a posteriori. Compare com a estimativa
de máxima verossimilhança
usando
uma aproximação para a média a posteriori. Compare com a estimativa
de máxima verossimilhança
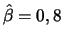 .
.
- Para o mesmo modelo do exercício 1 e os mesmos dados suponha
agora que a variância é desconhecida, i.e.
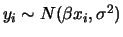 . Usamos uma priori hierárquica para
. Usamos uma priori hierárquica para
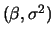 ,
i.e.
,
i.e.
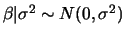 e
e
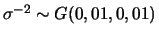 .
.
- Obtenha uma amostra da posteriori de
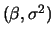 usando reamostragem
ponderada.
usando reamostragem
ponderada.
- Baseado nesta amostra, faça um histograma das distribuições
marginais de
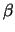 e
e 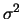 .
.
- Estime
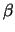 e
e 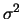 usando
uma aproximação para a média a posteriori. Compare com as estimativas
de máxima verossimilhança.
usando
uma aproximação para a média a posteriori. Compare com as estimativas
de máxima verossimilhança.



Next: A. Lista de Distribuições
Up: Introdução a Inferência Bayesiana
Previous: 4. Computação Bayesiana
Sumário
Ricardo Ehlers & Paulo Justiniano