Chapter 6 Modelos de regressão com efeitos aleatórios

A área de modelagem estatística teve um grande impulso com a criação dos modelos de regressão, dos quais os ilustrados no Capítulo ?? são alguns exemplos. As aplicações aparecem nas mais diversas áreas da ciência. Nesta diversidade de aplicações é muito fácil encontrar situações de relevância prática nas quais os modelos de regressão tradicionais deixam de ser adequados pela existência de características que violam suposições de modelos usuais. Alguns exemplos são:

  • para covariáveis contínuas, a suposição de efeito estritamente linear no preditor pode não ser adequada,
  • as observações podem ser correlacionadas no espaço,
  • as observações podem ser correlacionadas no tempo,
  • interações complexas podem ser necessárias para modelar o efeito conjunto de algumas covariáveis,
  • heterogeneidade entre indivíduos ou unidades pode não ser suficientemente descrita por covariáveis.

Em tais situações a variabilidade das observações usualmente não segue a prescrita pelo modelo de probabilidades e a classe de modelos de regressão é estendida pela adição de efeitos aleatórios, incorporando variáveis não observadas (latentes). Esta abordagem é extensivamente utilizada por ser altamente flexível mas ainda preservando especificações de modelos entre distribuições conhecidas e tratáveis analítica e/ou computacionalmente. Esta classe de modelos pode facilmente ser descrita como uma extensão dos modelos de regressão com efeitos fixos, pela inclusão de mais uma suposição. Considere que \(Y\) seja um vetor de dimensão \(n\). A seguinte estrutura hierárquica descreve um modelo de regressão com efeitos aleatórios. Neste livro vamos nos limitar a inclusão de efeitos aleatórios gaussianos, como na seguinte especificação:

\[\begin{align*} [Y | b , X] &\sim f(\underline{\mu}, \phi) \\ g(\underline{\mu}) &= X \underline{\beta} + Z \underline{b} \\ \underline{b} &\sim NMV(\underline{0}, \Sigma) . \end{align*}\]

O preditor linear é decomposto em duas componentes, a parte de efeitos fixos \(X \underline{\beta}\) e a parte aleatória \(Z \underline{b}\). As matrizes de delineamento \(X\) e \(Z\) são consideradas conhecidas representando os efeitos de covariáveis de interesse. O vetor \(\underline{\beta}\) representa os efeitos fixos que deverão ser estimados. O vetor aleatório \(\underline{b}\) são quantidades não observadas (latentes) para o qual vamos atribuir uma distribuição gaussiana multivariada de média \(0\) e matriz de covariância \(\Sigma\). De acordo com a estrutura imposta a \(\Sigma\) podemos induzir diversos tipos de correlação entre as observações \(Y\). É usual adotar a suposição de independência condicional em \([Y|b]\), ou seja, dado os efeitos aleatórios as observações são independentes, o que é usado na construção da verossimilhança e explorado por algoritmos numéricos.

A inferência baseada em verossimilhança para esta classe de modelos apresenta desafios computacionais, principalmente quando a distribuição atribuída a variável resposta é diferente da gaussiana. Na discussão a seguir vamos, sem perda de generalidade, excluir a matriz de efeitos fixos \(X\). Como temos duas quantidades aleatórias, devemos obter a distribuição conjunta \([Y,b]\) que pode, seguindo a estrutura hierárquica do modelo, ser fatorada na forma \([Y,b] = [Y|b][b]\). Entretanto, apenas \(Y\) é observável e portanto a verossimilhança é dada pela distribuição marginal \([Y]\) que é obtida fazendo uma média sobre os valores da variável não observada \([Y] = \int [Y|b][b] db\). As estimativas são obtidas maximizando \([Y]\) em relação aos parâmetros do modelo. Sob a suposição de que \([b]\) é gaussiana multivariada, temos que os parâmetros do modelos são \([\underline{\beta}, \Sigma, \phi]\), ou seja, o vetor de efeitos fixos mais os parâmetros que indexam a distribuição do efeito aleatório tipicamente com algum parâmetro de variabilidade ou precisão.

Quando a distribuição de \([Y]\) não é gaussiana, não é possível resolver analiticamente a integral contida na função de verossimilhança e temos que recorrer a métodos numéricos. Isto implica que métodos de integração numérica são necessários para avaliar a verossimilhança marginal e obter as estimativas de máxima verossimilhança. Esta descrição é bastante genérica e será detalhada na sequência. Mas antes vamos apresentar um exemplo onde a distribuição de \([Y]\) e obter as estimativas de máxima verossimilhança. Esta descrição é bastante genérica e será detalhada na sequência. Mas antes vamos apresentar um exemplo onde a distribuição de \([Y]\) é gaussiana porém as amostras não são independentes.

6.1 Modelo geoestatístico

O termo geoestatística, refere-se a um conjunto de modelos e métodos para dados com as seguintes características: os valores \(Y_i : i = 1, \ldots,n\) são observados em um conjunto finito de localizações amostrais, \(x_i\), em alguma região espacial \(A\), mas que, potencialmente, podem ser medidos em qualquer ponto arbitrário \(x\) na área. Cada valor \(Y_i = Y(x_i)\) pode ser visto como uma versão ruidosa de um fenômeno espacial contínuo não observável (latente) \(S(\cdot)\), nas correspondentes localizações amostrais \(x_i\).

O objetivo mais comum neste tipo de análise é “recuperar” o processo latente \(S(x)\) o que normalmente pode ser feito obtendo-se predições \(\hat{E}[S(x)]\) da média do processo em cada localização. Este procedimento é genericamente conhecido pelo nome de krigagem. O modelo geoestatístico como apresentado, dentre diversos outros, em P. J. Diggle and Ribeiro Jr. (2007) pode ser definido como um modelo de efeitos aleatórios na forma considerada aqui. Vamos considerar a especificação do modelo para respostas gaussianas, embora a mesma estrutura seja válida com outras distribuições para a variável observável \(Y(\cdot)\).

\[\begin{align} \nonumber [Y|b, D] &\sim N(\underline{\mu}, {\rm I} \tau^2) \\ \underline{\mu} &= D \underline{\beta} + Z \underline{b} \\ \nonumber \underline{b} &\sim NMV(\underline{0}, \Sigma_b) \tag{6.1} \end{align}\] em que, \(D\) é uma matriz de covariáveis conhecidas com o vetor de parâmetros lineares \(\underline{\beta}\) associados a elas, como em um modelo de regressão linear usual. Associamos um efeito aleatório \(S(\underline{x})\) a cada posição o que pode ser denotado definindo uma matriz identidade em \(Z = {\rm diag}(1)\) e um vetor \(\underline{b}\), ambos de dimensão igual a \(n\), o número de observações. Portanto o modelo geoestatístico desta forma pode ser interpretado como um modelo de intercepto aleatório com um valor em cada localização. A parte deste modelo que merece mais atenção é a matriz \(\Sigma_b\) que descreve a estrutura da dependência espacial entre as observações. Tipicamente, os elementos desta matriz são dados por uma função de correlação cujo argumento é a distância entre cada par de observações. A literatura especializada apresenta diversas opções para escolha da função de correlação. Na sequência vamos usar a função de correlação exponencial \(\rho(||x_i - x_j||) = \exp\{-||x_i - x_j||/\phi\}\) em que o parâmetro \(\phi\) controla a velocidade do decaimento da correlação com o aumento da distância entre localizações. Por exemplo, a matriz considerando apenas três localizações espaciais, toma a seguinte forma: \[ \Sigma_b = \sigma^2 \cdot \begin{bmatrix} 1 & \exp(-u_{12}/\phi) & \exp(-u_{13}/\phi) \\ \exp(-u_{21}/\phi) & 1 & \sigma^2 \exp(-u_{23}/\phi) \\ \exp(-u_{31}/\phi) & \sigma^2 \exp(-u_{32}/\phi) & 1 \end{bmatrix} \] em que \(u_{ij}=||x_i - x_j||\) é a distância euclidiana entre as posições espaciais das variáveis \(Y(x_i)\) e \(Y(x_j)\). Portanto, a matriz de covariância completa parametrizada por \(\sigma^2\) e \(\phi\) é obtida a partir da matriz de distância entre todas as posições espaciais observadas na amostra. O parâmetro \(\phi\) controla a extensão da dependência espacial entre as observações (alcance), enquanto que o parâmetro \(\sigma^2\) é a variância dos efeitos aleatórios, nesta caso, o termo espacial do modelo. Em (6.1) é especificado um outro efeito aleatório não correlacionado tal que \(\epsilon_i \sim {\rm N}(0, \tau^2)\), como o termo de erro no modelo de regressão linear usual. Este último parâmetro de variância ao modelo, por vezes chamado de efeito de pepita, e pode ser interpretado como a soma de variações não especiais e de micro escala.

A inferência para os parâmetros envolvidos no modelo \(\underline{\theta} = (\underline{\beta}, \underline{\theta}^*)\) com \(\underline{\theta}^* = (\sigma^2, \tau^2, \phi)\), pode ser baseada na função de verossimilhança dada pela densidade da distribuição normal multivariada e portanto \(Y \sim NMV (D\underline{\beta} , \Sigma)\), com \(\Sigma = \Sigma_b + {\rm I}\tau^2\). Para ilustrar, a matriz para três observações fica: \[ \Sigma = \begin{bmatrix} \sigma^2 + \tau^2 & \sigma^2 \exp(-\frac{u_{12}}{\phi}) & \sigma^2 \exp(-\frac{u_{13}}{\phi}) \\ \sigma^2 \exp(-\frac{u_{21}}{\phi}) & \sigma^2 + \tau^2 & \sigma^2 \exp(-\frac{u_{23}}{\phi}) \\ \sigma^2 \exp(-\frac{u_{31}}{\phi}) & \sigma^2 \exp(-\frac{u_{32}}{\phi}) & \sigma^2 + \tau^2 \end{bmatrix}. \] Com isso, tem-se seguinte expressão para a função de verossimilhança, \[ L(\underline{\theta}) = (2\pi)^{-\frac{n}{2}} |\Sigma|^{-\frac{1}{2}} \exp\{ -\frac{1}{2} (Y - D\underline{\beta})^\top \Sigma^{-1} (Y - D \underline{\beta})\} . \] A função de log-verossimilhança fica,

\[\begin{equation} l(\underline{\theta}) = -\frac{n}{2} \log(2\pi) -\frac{1}{2} \log |\Sigma| - \frac{1}{2} (Y - D \underline{\beta})^\top \Sigma^{-1}(Y - D \underline{\beta}). \tag{6.2} \end{equation}\]

Para estimação dos parâmetros maximizamos (6.2) em relação a \(\underline{\theta}\). Temos em \(\underline{\theta}\) dois conjuntos de parâmetros, os associados à média (\(\underline{\beta}\)) e os associados a estrutura de variância e covariância (\(\sigma^2, \tau^2, \phi\)). A log-verossimilhança pode facilmente ser derivada em função de \(\underline{\beta}\). Já para o caso dos parâmetros que indexam a matriz \(\Sigma\), exceto por um parâmetro de escala,
a derivação não é tão trivial ou mesmo pode não ter expressão analítica fechada e vai depender do modelo da função de correlação. Derivando a função (6.2) em relação aos \(\underline{\beta}\) e igualando a zero, chegamos ao estimador de máxima verossimilhança:

\[\begin{equation} \hat{\underline{\beta}} = (D^\top \Sigma^{-1} D)^{-1} ( D^\top \Sigma^{-1}Y) \tag{6.3} \end{equation}\] Substituindo (6.3) em (6.2) obtemos a função de log-verossimilhança concentrada apenas nos parâmetros que definem a estrutura de variância e covariância do modelo. \[\begin{equation} l^*(\underline{\theta}^*) = -\frac{n}{2} \log ( 2\pi) - \frac{1}{2} \log | \Sigma | - \frac{1}{2} \hat{e}^\top \Sigma^{-1} \hat{e} \tag{6.4} \end{equation}\] com \(\hat{e} = (Y - D \hat{\underline{\beta}})\). Os três parâmetros em \(\underline{\theta}^*\) indexam a matriz \(\Sigma\), logo é necessário derivá-los usando cálculo matricial. É possível mostrar que a função escore é dada por, \[\begin{equation} \dfrac{ \partial l^*(\underline{\theta}^*; \underline{Y})}{ \partial \theta^*_i} = -\frac{1}{2} Tr \left[ \Sigma^{-1} \dfrac{ \partial \Sigma}{ \partial \theta_i^*} \right] - \frac{1}{2} \hat{\underline{e}}^\top \left[ - \Sigma^{-1} \dfrac{ \partial \Sigma}{ \partial \theta_i^*} \Sigma^{-1}\right] \hat{\underline{e}}, \quad i = 1, \ldots,3. \tag{6.5} \end{equation}\] em que as matrizes \(\dfrac{ \partial \Sigma}{ \partial \theta_i^*}\) são obtidas derivando cada elemento a matriz \(\Sigma\) em relação ao respectivo parâmetro. Para exemplificar, com duas observações. a derivada de \(\Sigma\) em relação ao parâmetro \(\sigma\) é a matriz: \[ \frac{\partial \Sigma}{\partial \sigma} = 2 \sigma \begin{bmatrix} 1 & \exp(-\frac{u_{12}}{\phi}) \\ \exp(-\frac{u_{21}}{\phi}) & 1 \end{bmatrix}. \] Para o parâmetro \(\tau\) obtemos: \[ \frac{\partial \Sigma}{\partial \tau} = 2 \tau \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} , \] finalmente em relação ao parâmetro \(\phi\) \[ \frac{\partial \Sigma}{\partial \phi} = \frac{\sigma^2}{\phi^2} \begin{bmatrix} 0 & u_{12} \exp(-\frac{u_{12}}{\phi}) \\ u_{21} \exp(-\frac{u_{21}}{\phi}) & 0 \end{bmatrix}. \]

Utilizamos esses resultados para implementação do modelo geoestatístico gaussiano. Iniciamos definindo a função montaSigma() que constrói a matriz \(\Sigma\) do modelo geoestatístico a partir dos parâmetros e da matriz de distâncias euclidianas entre as localizações.

Código 6.1 Função para construir a matriz de variância-covariância para o modelo geoestatístico com função de correlação exponencial. 
 montaSigma <- function(s, t, phi, Umat){
   Sigma <- as.matrix(s^2 * exp(-Umat/phi))
   diag(Sigma) <- s^2 + t^2
   return(Sigma)
 }

No código 6.2 definimos uma função para simular dados segundo o modelo considerado. Na função simula.geo() começamos simulando as coordenadas \(x\) com localizações no quadrado unitário.

Com as coordenadas, calculamos a matriz \(U\) de distância entre todos os pontos a partir da qual montamos a matriz \(\Sigma\) de covariância. Obtemos uma simulação da distribuição normal multivariada por \(Y = D \underline{\beta} + \Sigma^{1/2} z\) em que \(\underline{z}\) são escores da normal padrão \(N(0,1)\) e \(\Sigma^{1/2}\) é alguma raiz da matriz de covariâncias. Utilizamos aqui \(\Sigma^{1/2} = R'\) tal que \({\rm Var(R'\underline{z}) = R'{\rm Var}(z)}R = R'R = \Sigma\) em que \(R\) é a parte superior da decomposição de Cholesky calculada no R por chol(). Desta forma, geramos dados do modelo geoestatístico com função de correlação exponencial.

Código 6.2 Função para simular do modelo geoestatístico. 
 simula.geo <- function(beta, s, t, phi, n){
   locs <- data.frame(cX = runif(n), cY = runif(n))
   U <- dist(locs, diag=TRUE, upper=TRUE)
   Sigma <- montaSigma(s=s, t=t, phi=phi, Umat=U)
   z <- rnorm(n)
   Y = beta + crossprod(chol(Sigma), z) 
   return(cbind(locs, Y=Y))
 }

Vamos obter uma simulação supondo que a estrutura de média é composta por apenas um parâmetro \(\beta_0 = 50\) e definimos \(\sigma^2 = 2^2\), \(\tau^2 = 1^2\) e \(\phi = 0.25\). A seguinte chamada simula \(125\) amostras do modelo geoestatístico usando o código 6.2.

 set.seed(12)
 dt <- simula.geo(b=50, s=2, t=1, phi=0.25, n=125)

O próximo passo para inferência é a definição da função de log-verossimilhança concentrada como no código 6.3. Com isto podemos maximizar a log-verossimilhança diretamente através da optim() ou qualquer outra forma de maximização numérica.

Código 6.3 Função de log-verossimilhança para o modelo geoestatístico. 
 ll.geo <- function(s, t, phi, dados){
  U <- dist(dados[,1:2], diag=TRUE, upper=TRUE)
  Sigma <- montaSigma(s=s, t=t, phi=phi, Umat=U)
  D <- as.vector(rep(1,length=nrow(dados)))
  invSD <- solve(Sigma, D)
  bhat <- solve(crossprod(invSD, D),crossprod(invSD,dados$Y))
  require(mvtnorm)
  ll = dmvnorm(dados$Y, mean=D%*%bhat, sigma=Sigma, log=TRUE)
  return(-ll)
 }

Este código ilustra passo a passo e didaticamente os cálculos envolvidos na expressão (6.4). Entretanto, o código é pouco eficiente computacionalmente por fazer algumas operações desnecessariamente e/ou de maneira pouco eficiente. Tipicamente a função de verossimilhança é avaliada diversas vezes em algum procedimento numérico. Como a matriz \(U\) é constante deve ser informada como argumento, evitando ser recalculada desnecessariamente a cada iteração. A obtenção de \(\hat{\beta}\) por (6.3) requer a inversão da matriz de covariância que pode ser escrita na forma da solução de um sistema. No código acima \(\Sigma^{-1} D\) é computado por solve(Sigma, D). Ainda sim há computações desnecessárias pois para resolver este sistema é feita uma decomposição de que é repetida dentro da chamada dmvnorm(). Isto é relevante uma vez que as operações com \(\Sigma\) são as mais caras na computação deste modelo. Desta forma, reescrevemos a função no código 6.4 fazendo ainda generalizações para nomes de variáveis e definição da matriz \(D\) e incluindo a opção para estimar os parâmetros na escala logarítmica.

Código 6.4 Redefinição da função de log-verossimilhança para o modelo geoestatístico. 
 ll.geo <- function(s, t, phi, modelo, Umat, dados, logpars = F) {
     if (logpars) {
         s <- exp(s)
         t <- exp(t)
         phi <- exp(phi)
     }
     mf <- model.frame(modelo, dados)
     y <- model.response(mf)
     D <- model.matrix(modelo, mf)
     Sigma <- montaSigma(s = s, t = t, phi = phi, Umat = Umat)
     R <- chol(Sigma)
     invRD <- backsolve(R, D, transpose = TRUE)
     invRy <- backsolve(R, y, transpose = TRUE)
     bhat <- solve(crossprod(invRD), crossprod(invRD, invRy))
     invRe <- invRy - invRD %*% bhat
     nll <- drop(length(y) * log(2 * pi)/2 + sum(log(diag(R))) + 
         crossprod(invRe)/2)
     return(nll)
}

Como temos as expressões (6.5) dos gradientes analíticos, vamos implementá-las para melhorar o desempenho do algoritmo de maximização numérica. Veremos o efeito na comparação dos tempos computacionais para convergência com e sem o uso do gradiente analítico. Para utilizar o gradiente precisamos primeiro implementar três funções com as matrizes de derivadas em relação a cada um dos parâmetros em \(\underline{\theta}^*\).

Código 6.5 Funções para definição dos gradientes do modelo geoestatístico. 
 ## Derivada de sigma, tau e phi
 deriv.s <- function(s, t, phi, Umat){
   Sigma.s <- 2*s*as.matrix(exp(-Umat/phi))
   diag(Sigma.s) <- 2*s
   return(Sigma.s)}
 deriv.t <- function(s, t, phi, Umat){
   return(diag(2*t, nrow(as.matrix(Umat))))}
 deriv.phi <- function(s, t, phi, Umat){
   return(s^2 * as.matrix(Umat) * exp(-as.matrix(Umat)/phi)/phi^2)}

Implementamos a função escore completa em 6.6.

Código 6.6 Função escore para o modelo geoestatístico. 
 escore <- function(s, t, phi, modelo, Umat, dados, logpars = F) {
     if (logpars) {
         s <- exp(s)
         t <- exp(t)
         phi <- exp(phi)
     }
     mf <- model.frame(modelo, dados)
     y <- model.response(mf)
     D <- model.matrix(modelo, mf)
     Sigma <- montaSigma(s = s, t = t, phi = phi, U = Umat)
     R <- chol(Sigma)
     invRD <- backsolve(R, D, transpose = TRUE)
     invRy <- backsolve(R, y, transpose = TRUE)
     bhat <- solve(crossprod(invRD), crossprod(invRD, invRy))
     invRe <- invRy - invRD %*% bhat
     e.hat <- y - D %*% bhat
     Sigma1 <- chol2inv(R)
     S1D <- Sigma1 %*% deriv.s(s = s, t = t, phi = phi, U = Umat)
     U.s <- 0.5 * (sum(diag(S1D)) - crossprod(e.hat, S1D %*% 
         Sigma1) %*% e.hat)
     T1D <- Sigma1 %*% deriv.t(s = s, t = t, phi = phi, U = Umat)
     U.t <- 0.5 * (sum(diag(T1D)) - crossprod(e.hat, T1D %*% 
         Sigma1) %*% e.hat)
     P1D <- Sigma1 %*% deriv.phi(s = s, t = t, phi = phi, 
         U = Umat)
     U.phi <- 0.5 * (sum(diag(P1D)) - crossprod(e.hat, P1D %*% 
         Sigma1) %*% e.hat)
     return(c(U.s, U.t, U.phi))
 }

Tanto na função escore como na log-verossimilhança concentrada retornamos o negativo da função para compatibilidade com a função mle2() que por default minimiza a função objetivo.

Com tudo implementado utilizamos o conjunto de dados simulados e ajustamos o modelo usando a função mle2() do pacote bbmle por conveniência. Alternativamente, poderíamos usar diretamente a função optim() com qualquer um de seus algoritmos, ou mesmo outros maximizadores disponíveis no R. Nos comandos a seguir, estimamos os parâmetros sem e depois com o uso do gradiente analítico pelo algoritmo L-BFGS-B e comparamos os tempos computacionais.

 require(bbmle)
 system.time(est1 <- mle2(ll.geo, start = list(s = 1, t = 0.1, 
     phi = 0.1), method = "L-BFGS-B", lower = list(s = 0, 
     t = 0, phi = 0), data = list(dados = dt, modelo = Y ~ 
     1, Umat = dist(dt[, 1:2], upper = T, diag = T))))
##    user  system elapsed 
##   0.318   0.000   0.318
 system.time(est2 <- mle2(ll.geo, gr = escore, start = list(s = 1, 
     t = 0.1, phi = 0.1), method = "L-BFGS-B", lower = list(s = 0, 
     t = 0, phi = 0), data = list(dados = dt, modelo = Y ~ 
     1, Umat = dist(dt[, 1:2], upper = T, diag = T))))
##    user  system elapsed 
##   0.869   0.000   0.870

Neste caso, o uso do gradiente analítico diminuiu o tempo para a maximização da log-verossimilhança. Este ganho pode ser expressivo, principalmente com grandes bases de dados e/ou procedimentos computacionalmente intensivos. Entretanto, o uso do gradiente nem sempre é vantajoso ou proporciona um incremento de velocidade da mesma ordem deste exemplo, pois a avaliação da função escore também exige cálculos matriciais. Para um melhor desempenho o código das funções de verossimilhança e escore podem (e devem!) ser reescritos para aproveitar na escore os cálculos já realizados na avaliação função de verossimilhança. O mecanismos do R de criar e acessar dados de ambiente (environments) podem ser usados aqui. Fazemos esta implementação nos complementos online.

Informações do ajuste são resumidas a seguir.

 summary(est1)
## Maximum likelihood estimation
## 
## Call:
## mle2(minuslogl = ll.geo, start = list(s = 1, t = 0.1, phi = 0.1), 
##     method = "L-BFGS-B", data = list(dados = dt, modelo = Y ~ 
##         1, Umat = dist(dt[, 1:2], upper = T, diag = T)), lower = list(s = 0, 
##         t = 0, phi = 0))
## 
## Coefficients:
##     Estimate Std. Error z value   Pr(z)    
## s      1.912      0.459    4.16 3.2e-05 ***
## t      1.128      0.128    8.81 < 2e-16 ***
## phi    0.333      0.202    1.65     0.1 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## -2 log L: 471

Com as estimativas dos parâmetros de covariância pode-se obter a estimativa de \(\underline{\beta}\) (neste caso um escalar) por (6.3) e sua variância \({\rm Var}(\hat{\beta}) = (D^\top \Sigma^{-1} D)^{-1}\) como mostrado a seguir. Note que este cálculo já é feito internamente na função que avalia a verossimilhança.

 D <- model.matrix(Y ~ 1, data=dt)
 Dmat <- as.matrix(dist(dt[,1:2], upper=T, diag=T))
 Sigma <- montaSigma(s=coef(est1)[1], t=coef(est1)[1], 
                      phi=coef(est1)[1], Umat=Dmat)
 R <- chol(Sigma)
 invRD <- backsolve(R, D, transpose=TRUE)
 invRy <- backsolve(R, dt[,3], transpose=TRUE)
 (drop(beta.est <- solve(crossprod(invRD),crossprod(invRD, invRy))))
## [1] 49.4
 (drop(var.beta.est <- solve(crossprod(invRD))))
## [1] 2.68

Para finalizar o procedimento de inferência no modelo geoestatístico a Figura 6.1 apresenta os perfis de verossimilhança para os parâmetros que indexam a matriz de variância/covariância do modelo. Observa-se assimetria em \(\phi\) e \(\sigma\). Estes parâmetros são não ortogonais na parametrização usada o que pode ser visto em verossimilhanças conjuntas (não mostradas aqui). Parametrizações alternativas são sugeridas na literatura e usualmente utilizam um novo parâmetro definido pelo quociente entre \(\phi\) e \(\sigma\). O parâmetro é usualmente ortogonal aos demais \(\tau\) e por vezes a estimativa está próxima ao limite do espaço paramétrico. Mais notadamente o perfil de verossimilhança para \(\phi\) cresce muito lentamente ou deixa de crescer para valores a direita. Isto reflete o fato deste parâmetro estar relacionado às distâncias entre localizações na área e não há informação estatística para distâncias além dos limites da área.

Verossimilhanças com aspecto distante do quadrático são comuns para alguns parâmetros de modelos com efeitos espaciais. Pode-se tentar atenuar os efeitos fazendo reparametrizações, por exemplo, estimar o \(\log(\tau)\) ou alguma outra função adequada, mas em geral há pouca informação na amostra sobre certos parâmetros do modelo.
Não há uma “receita” geral para todos os modelos, mas a inspeção de superfícies e verossimilhanças perfilhadas podem sugerir as melhores parametrizações.

Perfis de verossimilhança para o modelo geoestatístico.

Figura 6.1: Perfis de verossimilhança para o modelo geoestatístico.

6.2 Verossimilhança Marginal

Os modelos mistos lineares generalizados são os modelos de regressão com efeitos aleatórios mais comumente usados, que estendem os mistos com resposta gaussiana para distribuições na família exponencial como nos modelos lineares generalizados. O objetivo desta Seção é descrever a formulação de um modelo de regressão com efeitos aleatórios de uma forma geral. Modelos para dados longitudinais, medidas repetidas, modelos com efeitos espaciais, temporais e espaço temporais podem ser descritos todos na mesma estrutura tratando de uma forma unificada uma ampla classe de modelos estatísticos.

A seguir, vamos descrever o modelo no contexto de dados agrupados e conforme necessário vamos indicando pequenas mudanças que geram modelos conhecidos, por exemplo, para dados longitudinais e espaciais. Seja \(Y_{ij}\) a \(j\)-ésima medida para a unidade amostral \(i, i = 1, \ldots, N\) , \(j = 1, \ldots, n_i\) e \(\underline{Y}_i\) o vetor \(n_i\)-dimensional de todas as medidas realizadas na unidade amostral \(i\). Assumindo independência condicional no vetor \(q\)-dimensional de efeitos aleatórios \(\underline{b}_i\), para o qual atribuímos uma distribuição \(NMV_q(\underline{0}, \Sigma)\), as respostas \(Y_{ij}\) são independentes com densidade da forma,

\[ f_i(y_{ij} | \underline{b}_i, \underline{\beta}, \phi), \]

com \(g(\mu_{ij}) = \mathbf{x}_{ij}^T \boldsymbol{\underline{\beta}} + \mathbf{z}_{ij}^T \mathbf{\underline{b}_i}\) para uma função de ligação \(g(\cdot)\) conhecida, com \(\mathbf{x}_{ij}\) e \(\mathbf{z}_{ij}\) vetor de covariáveis conhecidas de dimensão \(p\) e \(q\) respectivamente, \(\boldsymbol{\underline{\beta}}\) um vetor p-dimensional de coeficientes de regressão fixos desconhecidos, e \(\phi\) algum parâmetro extra na verossimilhança, geralmente indicando precisão ou variância. Para completar a especificação do modelo, seja \(f(\mathbf{\underline{b}_i}|\Sigma)\) a densidade da \(NMV_q(\mathbf{0},\Sigma)\) distribuição atribuída para os efeitos aleatórios \(\mathbf{\underline{b}_i}\).

Como já mencionado, a estimação dos parâmetros envolvidos no modelo pode ser feita maximizando a verossimilhança marginal, com a integração dos efeitos aleatórios. A contribuição para a verossimilhança da cada unidade amostral (grupo) é: \[ f_i(\underline{y}_i | \underline{\beta}, \Sigma, \phi) = \int \prod_{j=1}^{n_i} f_{ij}(y_{ij} | \underline{b}_i, \underline{\beta}, \phi) f(\underline{b}_i | \Sigma)d \underline{b}_i , \] a verossimilhança completa para \(\underline{\beta}\), \(\Sigma\) e \(\phi\) é dada por

\[\begin{equation} L(\underline{\beta}, \Sigma, \phi) = \prod_{i=1}^N f_i(\underline{y}_i | \underline{\beta}, \Sigma, \phi) , \tag{6.6} \end{equation}\]

e sob a suposição de independência entre os grupos temos que \[\begin{equation} L(\underline{\beta}, \Sigma, \phi) = \prod_{i=1}^N \int \prod_{j=1}^{n_i} f_{ij}(y_{ij} | \underline{b}_i, \underline{\beta}, \phi) f(\underline{b}_i | \Sigma) d \underline{b}_i . \tag{6.7} \end{equation}\]

A principal dificuldade em maximizar (6.6) é a presença das \(N\) integrais sobre os efeitos aleatórios \(q\)-dimensionais. Em alguns casos especiais estas integrais podem ser resolvidas analiticamente, como no caso do modelo geoestatístico em 6.1 e, de forma geral, modelos com resposta gaussiano. Porém, na maioria das situações onde a resposta é não gaussiana as integrais envolvidas no cálculo da função de verossimilhança não tem solução analítica.

Além disso, um problema adicional é a dimensão do vetor de efeitos aleatórios. Quando \(q\) é pequeno, o que acontece em modelos de regressão com somente o intercepto aleatório (\(q=1\)) ou inclinação aleatória (\(q=2\) para uma única covariável) as integrais são passíveis de ser resolvidas por métodos de integração numérica convencionais, como Gauss-Hermite, Laplace e Monte Carlo. Estes métodos serão abordados na sequência. Porém, em alguns modelos, como por exemplo os modelos espaciais, a dimensão do vetor aleatório pode chegar a \(q = N\), ou seja, o vetor tem a dimensão do tamanho da amostra, possivelmente grande, o que torna os métodos convencionais de integração numérica não aplicáveis. Métodos de integração numérica como Gauss-Hermite e Monte Carlo vão ser úteis quando a dimensão do vetor de efeitos aleatórios é pequena, digamos, menor que seis. Para efeitos aleatórios de maior dimensão uma implementação muito cuidadosa do método de Laplace pode ser adequada em algumas situações.

Em modelos onde o vetor de efeitos aleatórios é de grande dimensão o mais usual é lançar mão de métodos que avaliam a verossimilhança por algoritmos de amostragem. Neste contexto os métodos MCMC - Monte Carlo via Cadeias de Markov - são extremamente poderosos para ajustar modelos de alta complexidade podendo ser usados para inferência baseada apenas na função de verossimilhança, ou na sua forma mais usual, sob o paradigma bayesiano.

Na sequência vamos apresentar alguns métodos tradicionais de integração numérica, que podem ser usados quando ajustamos modelos de efeitos aleatórios de baixa complexidade na estrutura aleatória. Os métodos serão aplicados na estimação de alguns modelos simples para medidas repetidas e dados longitudinais não gaussianos. Vamos iniciar com um modelo simples mais que serve de exemplo para apresentação dos métodos.

6.2.1 Simulação da Poisson com intercepto aleatório

Em todos os métodos de integração numérica que serão apresentados vamos utilizar o modelo de Poisson com intercepto aleatório definido em (6.8) para exemplificar o cálculo numérico. Para isto, precisamos de amostras deste modelo para podermos avaliar a função de verossimilhança para uma dada configuração de parâmetros, que é o objetivo final do uso dos métodos de integração numérica em modelos de regressão com efeitos aleatórios. A função simPois() simula amostras deste modelo de acordo com a parametrização usada.

Código 6.7 Função para simular variáveis aleatórias de um modelo de Poisson com efeito aleatório de intercepto. 
 simPois <- function(f.fixo, f.aleat, beta.fixo, prec.pars, data){
   X <- model.matrix(f.fixo, data)
   Z <- model.matrix(f.aleat, data)
   n.bloco <- ncol(Z)
   n.rep <- nrow(Z)/n.bloco
   bi <- rnorm(n.bloco,0,sd=1/prec.pars)
   XZ <- cbind(X,Z)
   beta <- c(beta.fixo,bi)
   preditor <- XZ%*%beta
   lambda <- exp(preditor)
   y <- rpois(length(lambda),lambda=lambda)
   return(cbind(y=y, data))
 }

Para simular do modelo precisamos das matrizes de delineamento \(X\) e \(Z\) e dos parâmetros \(\beta_0\) e \(\tau\). De acordo com o tamanho das matrizes \(X\) e \(Z\) a função identifica quantas unidades amostrais e quantas repetições por unidade amostral devem ser simuladas. Feita a função podemos usá-la.

 dt <- data.frame(ID=as.factor(rep(1:10,each=10)))
 set.seed(123)
 dados <- simPois(f.fixo=~1, f.aleat=~-1 + ID, 
                  beta.fixo = 2, prec.pars=3, data=dt)

De acordo com o código acima, foram simuladas \(10\) unidades amostrais e, em cada uma destas unidades, são retiradas \(10\) amostras totalizando \(100\) observações. O modelo tem uma média geral igual a 2 e atribui a cada grupo um desvio (efeito aleatório) deste valor. Neste exemplo, para cada avaliação da verossimilhança devemos resolver \(10\) integrais uma para cada unidade amostral. Nos exemplos, vamos usar apenas uma unidade amostral e fixar os parâmetros nos valores simulados para avaliar a integral. A função integrando escrita de forma vetorial, fica dada por:

Código 6.8 Integrando da função de verossimilhança do modelo de regressão de Poisson com efeito aleatório de intercepto. 
 integrando <- function(b, f.fixo, beta.fixo, prec.pars, 
                        log=TRUE, dados){
   mf <- model.frame(f.fixo, dados)
   y <- model.response(mf)
   X <- model.matrix(f.fixo, mf)
   tau <- exp(prec.pars)
   ll <- sapply(b,function(bi){
      preditor <- X%*%beta.fixo + bi
      lambda <- exp(preditor)   
      sum(dpois(y, lambda=lambda, log=TRUE)) + 
                 dnorm(bi, 0, sd=1/tau,log=TRUE)})
   if(log == FALSE) ll <- exp(ll)
   return(ll)
 }

Escrever a função em forma vetorial, significa simplesmente que podemos passar um vetor de valores e que a função será avaliada em cada um destes valores. Outro fato importante na forma de escrever o integrando é fazer o máximo possível das operações em escala logarítmica. Isso evita problemas com representações numéricas. Porém devemos sempre ter em mente que estamos calculando a integral na escala original e nunca em logaritmo. Por exemplo,

 ## Escala original
 integrando(b=c(-1,0,1), f.fixo = y~1, dados = subset(dados, ID == 1),
            beta.fixo = 2, prec.pars=4, log=FALSE)
## [1] 0.00e+00 4.01e-09 0.00e+00
 ## Escala log
 integrando(b=c(-1,0,1), f.fixo = y~1, dados = subset(dados, ID == 1),
            beta.fixo = 2, prec.pars=4, log=TRUE)
## [1] -1535.1   -19.3 -1564.8

O formato vetorial da função facilita a construção de algoritmos para integração numérica. É conveniente fazer um gráfico da função integrando para termos uma ideia do formato da função que estamos integrando. A Figura 6.2 apresenta o gráfico do integrando avaliado para cada uma das \(10\) unidades amostrais simuladas, o eixo \(y\) foi padronizado para poder colocar todas as funções no mesmo gráfico.

Integrando de acordo com unidade amostral - Modelo Poisson com intercepto aleatório.

Figura 6.2: Integrando de acordo com unidade amostral - Modelo Poisson com intercepto aleatório.

6.3 Técnicas de integração numérica

A necessidade de resolver uma integral numericamente aparece com bastante frequência quando ajustamos modelos de regressão com efeitos aleatórios. Como exemplo ilustrativo, escolhemos o modelo de regressão Poisson com intercepto aleatório, por ser um modelo simples, contendo apenas dois parâmetros o que permite construir gráficos de contornos da verossimilhança e sua aproximação quadrática. Este modelo pode ser usado para dados que apresentem uma variância maior do que a prevista no modelo de Poisson, ou seja, dados sobredispersos. O modelo tem a seguinte forma:

\[\begin{align} Y_{ij}|b_i &\sim P(\lambda_{i}) \\ \nonumber \log(\lambda_{i}) &= \beta_0 + b_i \\ \nonumber b_i &\sim N(0, 1/\tau^2) , \tag{6.8} \end{align}\]

em que \(\beta_0\) é o intercepto, \(b_i\) o efeito aleatório e \(\tau^2\) o parâmetro de precisão. Lembre-se que \(i = 1, \ldots, N\) indica o número de unidades amostrais e \(j=1,\ldots,n_i\) indica o número de medidas feitas na unidade amostral \(i\). Neste caso, a contribuição para a verossimilhança de cada unidade amostral é dada por:

\[\begin{align} \nonumber f_i( y_{ij} | b_i , \beta_0) &= \int_{-\infty}^{\infty} \frac{ \exp\{-\lambda_{i}\} \lambda_{i}^{ y_{ij}}}{y_{ij} !} \left( \frac{\tau}{2 \pi} \right)^{1/2} \exp\{- \frac{\tau^2}{2} b_i^2\} d b_i \\ \nonumber &= \int_{-\infty}^{\infty} \frac{\exp\{-\exp(\beta_0 + b_i)\} \exp\{(\beta_0 + b_i)^{y_{ij}}\}}{y_{ij} !} \\ & \hspace{2cm} \left( \frac{\tau}{2 \pi} \right)^{1/2} \exp\{- \frac{\tau^2}{2} b_i^2\} d b_i. \tag{6.9} \end{align}\]

A integral em (6.9) tem apenas uma dimensão e precisa ser resolvida para cada uma das \(N\) unidades amostrais, e isto é repetido em cada passo de algum algoritmo de maximização numérica. Vamos usar esta integral para ilustrar diversos métodos de integração numérica e posteriormente utiliza-los para estimar os parâmetros do modelo de Poisson com intercepto aleatório.

Diversos métodos de integração numérica podem ser encontrados em textos clássicos de cálculo numérico. O método do retângulo, dos trapézios, do ponto central e suas diversas variações, são métodos simples de serem implementados. Porém, na situação de modelos de regressão com efeitos aleatórios são de pouca valia, devido a restrição de que a integral a ser resolvida deve ser própria com limites finitos e fixados. Este não é o caso na equação (6.9). No uso destes métodos não resolvemos a integral na reta real, mas sim em um domínio finito adequado da função no integrando. Por exemplo, se é razoável assumir que quase toda a massa da distribuição está contida em \([-10, 10]\), avaliamos a integral neste intervalo.

Dentre os diversos métodos possíveis optamos por descrever o método trapezoidal de Simpson, a Quadratura Gaussiana usando os polinômios de Hermite, próprios para a integração na reta real, os Métodos baseados em simulação, integração Monte Carlo e Quase Monte Carlo, além da aproximação de Laplace. Combinando o método da Quadratura Gaussiana com a aproximação de Laplace, chegamos à Quadratura Adaptativa e o mesmo pode ser feito combinando Quase Monte Carlo com Laplace para obter um Quase Monte Carlo adaptativo.

6.3.1 Método Trapezoidal

O método trapezoidal consiste no uso de uma função linear para aproximar o integrando ao longo do intervalo de integração. O uso do polinômio de Newton entre os pontos \(x = a\) e \(x = b\) resulta em: \[ f(x) \approx f(a) + (x - a) \left[ \frac{f(b) - f(a)}{ b - a} \right]. \] Com a integração analítica, obtém-se: \[\begin{eqnarray*} I(f) &\approx& \int_a^b f(a) + (x - a)\left[ \frac{f(b) - f(a)}{ b - a} \right] dx \\ &=& f(a) (b - a) + \frac{1}{2}[f(b) - f(a)](b - a) \end{eqnarray*}\] Simplificando o resultado, obtém-se uma fórmula aproximada popularmente conhecida como regra ou método trapezoidal. \[\begin{equation} I(f) \approx \frac{[f(a) + f(b)]}{2} (b - a) \tag{6.10} \end{equation}\]

A expressão em (6.10) é extremamente simples de ser usada, requer apenas duas avaliações da função integrando. Sua versão em R pode ser escrita como se segue.

Código 6.9 Função para integração numérica por meio do método dos trapézios. 
 trapezio <- function(integrando, a, b, ...){
   Int <- ((integrando(a, ...) + integrando(b, ...))/2)*(b-a)
   return(Int)
 }

Podemos agora usar o método trapezoidal para avaliar a integral do modelo Poisson com intercepto aleatório no intervalo \([-0,5 ; 0,5]\).

 log(trapezio(integrando = integrando, a = -0.5, b = 0.5, f.fixo = y~1, 
     dados= subset(dados, ID == 1), beta.fixo = 2, prec.pars=4, log=FALSE))
## [1] -400

Este método é extremamente simples e serve apenas para apresentar as ideias gerais de integração numérica. Na sequência veremos que o resultado apresentado por este método é muito ruim.

6.3.2 Método de Simpson \(1/3\)

Neste método, um polinômio de segunda ordem é usado para aproximar o integrando. Os coeficientes de um polinômio quadrático podem ser determinados a partir de três pontos. Para uma integral ao longo do domínio \([a,b]\), são usados os dois pontos finais \(x_1 = a\), \(x_3 = b\), e o ponto central, \(x_2 = (a+b)/2\). O polinômio pode ser escrito na forma:

\[\begin{equation} p(x) = \alpha + \beta(x - x_1) + \lambda(x - x_1)(x - x_2) \tag{6.11} \end{equation}\]

onde \(\alpha\), \(\beta\) e \(\lambda\) são constantes desconhecidas avaliadas a partir da condição que diz que o polinômio deve passar por todos os pontos, \(p(x_1) = f(x_1)\), \(p(x_2) = f(x_2)\) e \(p(x_3) = f(x_3)\). Isso resulta em:

\[\begin{equation*} \alpha = f(x_1), \quad \beta = [ f(x_2) - f(x_1)] / (x_2 - x_1) \quad \text{e} \quad \lambda = \frac{f(x_3) - 2 f(x_2) + f(x_1)}{2(h)^2} \end{equation*}\] onde \(h = (b-a)/2\). Substituindo as constantes de volta em e integrando \(p(x)\) ao longo do intervalo \([a,b]\), obtém-se \[\begin{equation*} I = \int_{x_1}^{x_3} f(x) dx \approx \int_{x_1}^{x_3} p(x) dx = \frac{h}{3} \left[ f(a) + 4 f(\frac{a+b}{2}) + f(b) \right]. \end{equation*}\]

Note que, para o cálculo da integral é necessário apenas três avaliações da função, o que torna o método muito rápido. Podemos também facilmente implementar este método para integrar uma função qualquer, tal função terá como seus argumentos os limites \([a,b]\) e a função a ser integrada.

Código 6.10 Função para integração numérica por meio do método de Simpson. 
 simpson <- function(integrando, a, b, ...){
   h <- (b-a)/2
   x2 <-(a+b)/2
   integral <- (h/3)*(integrando(a,...) + 
                4*integrando(x2, ...) + integrando(b, ...))
   return(integral)
 }

Uma vez implementada a função podemos usá-la para integrar a nossa função de interesse. Lembre-se ainda que para o procedimento de maximização nos interessa o log do valor da integral e não a integral em log, por isso precisamos avaliar a função em sua escala original o que é computacionalmente incoveniente, mas necessário. Além disso, precisamos definir os limites de integração, neste caso fixamos \(-0.5\) a \(0.5\) tendo em mente o gráfico do integrando. Apenas para comparação dos resultados usamos a função integrate() do R.

 ## Escala original
 simpson(integrando = integrando, a = -0.5, b = 0.5, f.fixo = y~1, 
         dados=subset(dados,ID==1), beta.fixo=2, prec.pars=4, log=FALSE)
## [1] 2.67e-09
  ## Em log
 log(simpson(integrando = integrando, a = -0.5, b = 0.5, 
       f.fixo = y~1, dados=subset(dados, ID == 1),
       beta.fixo = 2, prec.pars=4, log=FALSE))
## [1] -19.7
  # Resultado com a integrate
 log(integrate(integrando, lower=-Inf, upper=Inf, f.fixo = y~1, 
     dados=subset(dados, ID == 1), beta.fixo = 2, 
       prec.pars=4, log=FALSE)$value)
## [1] -22.4

O resultado do método de Simpson é compatível com o obtido via integrate(), e bastante diferente do obtido pelo método do Trapézio. O mal desempenho do último é basicamente por este estar quase que totalmente voltado aos limites do intervalo de integração, que neste caso são definidos arbitrariamente. Se olharmos para a Figura 6.2 só a massa de probabilidade concentra-se em \([-0.1,0.1]\). Se integrarmos a função neste intervalo pelo método do Trapézio chegamos a um valor de -36.19794 mais próximo aos obtidos via Simpson e integrate(). O problema que enfrentamos aqui é como definir tais limites em situações práticas de forma geral. Esta é uma das grandes limitações destes métodos, mesmo em uma única dimensão. Outra grande limitação é como expandir estes métodos para integrais de dimensões maiores e como definir os limites em tais dimensões. O número de avaliações da função cresce exponencialmente com o número de dimensões da integral. Estes problemas, não são de fácil solução e motivaram diversos outros métodos que tentam contornar o problema mantendo um número razoável da avaliações a função.

6.3.3 Quadratura de Gauss-Hermite

Nos dois métodos de integração apresentados até agora, a integral de \(f(x)\) ao longo do intervalo \([a,b]\) foi avaliada representando \(f(x)\) como um polinômio de fácil integração. A integral é avaliada como uma soma ponderada dos valores de \(f(x)\) nos diferentes pontos. A localização dos pontos comuns é predeterminada em um dos métodos de integração. Até agora os dois métodos consideram pontos igualmente espaçados. Na quadratura de Gauss, a integral também é avaliada usando uma soma ponderada dos valores de \(f(x)\) em pontos distintos ao longo do intervalo \([a,b]\) (chamados pontos de Gauss). Estes pontos, contudo, não são igualmente espaçados e não incluem os pontos finais. O método de Gauss-Hermite é uma extensão do método de Quadratura Gaussiana para resolver integrais da forma: \[ \int_{-\infty}^{\infty} e^{-x^2} f(x) dx \]

Neste caso, a integral é aproximada por uma soma ponderada da função avaliada nos pontos de Gauss e pesos de integração. \[ \int_{-\infty}^{\infty} e^{-x^2} f(x) dx \approx \sum_{i=1}^n w_i f(x_i) \] onde \(n\) é o número de pontos usados para a aproximação. Os \(x_i\) são as raízes do polinômio de Hermite \(H_n(x) (i = 1< 2, \ldots, n )\) e os pesos \(w_i\) associados são dados por \[\begin{equation*} w_i = \frac{2^{n-1} n ! \sqrt{\pi}}{n^2 [H_{n-1}(x_i)]^2} \end{equation*}\]

Para a aproximação de integrais via o método de Gauss-Hermite precisamos dos pesos de integração \(w_i\) e dos pontos de Gauss \(x_i\). A função gauss.quad() do pacote statmod calcula os pesos e os pontos de Gauss-Hermite. A função abaixo, implementa o método de integração de Gauss-Hermite para uma função qualquer unidimensional.

Código 6.11 Função para integração numérica por meio do método de Gauss-Hermite unidimensional. 
 gauss.hermite <- function(integrando, n.pontos, ...){
   pontos <- gauss.quad(n.pontos, kind="hermite")
   integral <- sum(pontos$weights*integrando(pontos$nodes,...)
                   /exp(-pontos$nodes^2))
   return(integral)
 }

Esta função tem apenas dois argumentos, o primeiro é a função a ser integrada e o segundo o número de pontos a ser utilizado na aproximação. A segunda linha da função faz apenas uma soma ponderada da função avaliada nos pontos de Gauss. O método de Gauss-Hermite apresenta duas grandes limitações. A primeira está relacionada a escolha dos pontos de Gauss, que são escolhidos baseados em \(e\{-x^2\}\), independente da função \(f(x)\) no integrando. Dependendo do suporte de \(f(x)\), os pontos selecionados podem ou não estar dentro da área de interesse. Uma idéia natural é reescalonar os pontos de modo a colocá-los na área de maior densidade da função \(f(x)\) o que gera o método chamado de Quadratura Adaptativa de Gauss-Hermite, que veremos adiante. A Figura 6.3 ilustra o problema da definição dos pontos de integração.

Espalhamento dos pontos de integração pelo método de Gauss-Hermite.

Figura 6.3: Espalhamento dos pontos de integração pelo método de Gauss-Hermite.

Pela Figura 6.3 fica claro que para integrar a função em preto os pontos \((n=20)\) são satisfatórios, porém para a função em vermelho são claramente inadequados, já que, a área da função de maior massa não tem nenhum ponto de integração. Desta forma, para conseguir um resultado satisfatório é necessário aumentar muito o número de pontos de integração, encarecendo o procedimento. Vamos usar esta função para avaliar o valor da integral, contida no modelo Poisson com intercepto aleatório.

 ## Em log
 log(gauss.hermite(integrando = integrando, n.pontos=21, 
                   f.fixo = y~1, dados=subset(dados, ID == 1), 
                   beta.fixo = 2, prec.pars=4, log=FALSE))
## [1] -20.1

O segundo problema do método de Gauss-Hermite está relacionado com a dimensão da integral a ser resolvida. Quando a função é unidimensional, basta espalhar os pontos sobre a reta real e avaliar a função neste pontos. Para funções em duas ou mais dimensões precisamos do produto cartesiano dos pontos de integração para espalhar na função multidimensional, ou seja, o número de pontos cresce exponencialmente de acordo com a dimensão da função a ser integrada. Por exemplo, se em uma dimensão usamos \(20\) pontos para a integração em duas dimensões precisamos de \(20^2 = 400\), em três \(20^3 = 8000\). Isso mostra que para integrar funções multidimensionais o método de Gauss-Hermite torna rapidamente proibitivo. O método de Quadratura Adaptativa de Gauss-Hermite ameniza um pouco este problema, por requerer menos pontos de integração. Porém, o problema persiste para dimensões maiores que cinco ou seis, em geral. A função abaixo implementa o método de Gauss-Hermite para dimensões maiores que um.

Código 6.12 Função para integração numérica por meio do método de Gauss-Hermite multidimensional. 
 gauss.hermite.multi <- function(integrando,n.dim,n.pontos, ...){
 normaliza <- function(x){exp(-t(as.numeric(x))%*%as.numeric(x))}
 pontos <- gauss.quad(n.pontos,kind="hermite")
 nodes <- matrix(rep(pontos$nodes,n.dim),ncol=n.dim)
 pesos <- matrix(rep(pontos$weights,n.dim),ncol=n.dim)
 lista.nodes <- lista.pesos <- list()
 for(i in 1:ncol(nodes)){
  lista.nodes[[i]] <- nodes[,i]
  lista.pesos[[i]] <- pesos[,i]}
 nodes = as.matrix(do.call(expand.grid,lista.nodes))
 pesos = do.call(expand.grid,lista.pesos)
 pesos.grid = apply(pesos,1,prod)
 norma = apply(nodes,1,normaliza)
 integral <- sum(pesos.grid*(integrando(nodes,...)/norma))
 return(integral)
 }

Vamos usar a função gauss.hermite.multi() em uma dimensão apenas para exemplificar sua chamada.

 log(gauss.hermite.multi(integrando = integrando, n.pontos=21, n.dim=1,
                   f.fixo = y~1, dados=subset(dados, ID == 1), 
                   beta.fixo = 2, prec.pars=4, log=FALSE))
## [1] -20.1

6.3.4 Adaptativa Gauss-Hermite e Aproximação de Laplace

Com adaptativa Gauss-Hermite, os pontos de integração serão centrados e escalonados como se \(f(x) e^{-x^2}\) fosse a distribuição gaussiana. A média desta distribuição coincide com a moda \(\hat{x}\) de \(ln[f(x)e^{-x^2}]\), e a variância será igual a

\[ \begin{bmatrix} - \frac{\partial^2}{\partial x^2} ln[f(x)e^{-x^2}]|_{z=\hat{z}} \end{bmatrix}^{-1} . \] Assim, o novos pontos de integração adaptados serão dados por \[ x_i^+ = \hat{x} + \begin{bmatrix} - \frac{\partial^2}{\partial x^2} ln[f(x)e^{-x^2}]|_{x=\hat{x}} \end{bmatrix}^{-1/2} x_i \] com correspondentes pesos, \[ w_i^+ = \begin{bmatrix} - \frac{\partial^2}{\partial x^2} ln[f(x)e^{-x^2}]|_{z=\hat{z}} \end{bmatrix}^{-1/2} \frac{e^{x_i^+}}{e^{-x_i}} w_i . \] Como antes, a integral é agora aproximada por \[ \int f(x) e^{-x^2} dx \approx \sum_{i=1}^n w_i^+ f(x_i^+) \]

Quando integração de Gauss-Hermite ou adaptativa Gauss-Hermite é usada no ajuste de modelos de regressão com efeitos aleatórios, uma aproximação é aplicada para a contribuição na verossimilhança para cada uma das \(N\) unidades amostrais no conjunto de dados. Em geral, quanto maior a ordem de \(n\) pontos de integração melhor será a aproximação. Tipicamente, adaptativa Gauss-Hermite precisa de muito menos pontos que Gauss-Hermite. Por outro lado, adaptativa Gauss-Hermite requer o cálculo de \(\hat{x}\) para cada unidade amostral no conjunto de dados, assim a maximização numérica do integrando encarece bastante o custo computacional desta abordagem. Além disso, como o integrando é função dos parâmetros desconhecidos \(\underline{\beta}\),\(\Sigma\) e \(\phi\), os pontos de quadratura, bem como os pesos usados na adaptativa Gauss-Hermite dependem destes parâmetros, e assim precisam ser atualizados a cada passo de um processo de estimação iterativo, através de algum maximizador numérico, como os encontrados na função optim().

Um caso especial ocorre quando adaptativa Gauss-Hermite é aplicado com um ponto de integração. Denote \(f(x)e^{-x^2}\) por \(Q(x)\). Como \(n=1\), \(x_1 = 0\) e \(w_1 = 1\), obtemos \(x_1^+ = \hat{x}\), que é o máximo de \(Q(x)\). Além disso, os pesos de integração são iguais a \[ w_1^+ = | Q''(\hat{x}) |^{-1/2} \frac{e^{-\hat{x}}}{e^{-0}} = (2\pi)^{n/2} |Q''(\hat{x})|^{-1/2} \frac{e^{Q(\hat{x})}}{f(\hat{x})}. \]

Assim, a aproximação fica dada por \[\begin{align*} \int f(x) e^{-x^2} dx &= \int e^{Q(x)} dx \\ &\approx w_1^+ f(x_1^+) = (2\pi)^{n/2} |Q''(\hat{x})|^{-1/2} e^{Q(\hat{x})}, \end{align*}\] mostrando que a adaptativa Gauss-Hermite com um ponto de integração é equivalente a aproximar o integrando usando a Aproximação de Laplace. A função laplace() abaixo implementa a aproximação de Laplace para uma função qualquer.

Código 6.13 Função para integração numérica por meio do método de Laplace. 
 laplace <- function(funcao, otimizador,n.dim, ...){
   integral <- -999999
   inicial <- rep(0,n.dim)
   temp <- try(optim(inicial, funcao,..., method=otimizador, 
               hessian=TRUE, control=list(fnscale=-1)))
   if(class(temp) != "try-error"){
   integral <- exp(temp$value) * (exp((n.dim/2)*log(2*pi) - 
                   0.5*determinant(-temp$hessian)$modulus))}
   return(integral)
 }

Note a necessidade do uso da optim() para encontrar a moda da função e obter o Hessiano numérico. Importante notar que, na chamada para a integração via aproximação de Laplace a função integrando deve estar em escala logarítmica. A chamada abaixo, exemplifica esta aproximação.

 log(laplace(integrando, otimizador="BFGS", n.dim=1,
          f.fixo = y~1, dados=subset(dados, ID == 1), 
          beta.fixo = 2, prec.pars=4, log=TRUE))
## [1] -22.4
## attr(,"logarithm")
## [1] TRUE

Para finalizar com o uso de integração por Quadratura, a função adaptative.gauss.hermite() implementa a integração adaptativa de Gauss-Hermite para uma função qualquer.

Código 6.14 Função para integração numérica por meio do método de Gauss-Hermite multidimensional adaptativo. 
 adaptative.gauss.hermite <- function(funcao, n.dim, n.pontos, 
                                      otimizador, ... ){
 normaliza <- function(x){exp(-t(as.numeric(x))%*%as.numeric(x))}
 pontos <- gauss.quad(n.pontos,kind="hermite")
 integral <- -999999
 inicial <- rep(0,n.dim)
 temp <- try(optim(inicial, funcao,..., method=otimizador,
                   hessian=TRUE, control=list(fnscale=-1)))
 z.chapeu <- temp$par
 sd.chapeu <- sqrt(diag(solve(-temp$hessian)))
 mat.nodes <- matrix(NA, ncol=n.dim,nrow=n.pontos)
 mat.pesos <- matrix(NA,ncol=n.dim,nrow=n.pontos)
 for(i in 1:length(z.chapeu)){
   mat.nodes[,i] <- z.chapeu[i] + sd.chapeu[i]*pontos$nodes
   mat.pesos[,i] <- sd.chapeu[i] * 
     (exp(-mat.nodes[,i]^2)/exp(-pontos$nodes^2))*pontos$weights
 }
 lista.nodes <- list()
 lista.pesos <- list()
 for(i in 1:ncol(mat.nodes)){
  lista.nodes[[i]] <- mat.nodes[,i]
  lista.pesos[[i]] <- mat.pesos[,i]}
 nodes = as.matrix(do.call(expand.grid,lista.nodes))
 pesos = do.call(expand.grid,lista.pesos)
 pesos.grid = apply(pesos,1,prod)
 norma = apply(nodes,1,normaliza) 
 integral <- sum(pesos.grid*(exp(funcao(nodes,...))/norma))
 return(integral)
 }

Para comparar os resultados utilizamos a função usando diferentes quantidades de pontos de integração.

 ## 1 ponto
 log(adaptative.gauss.hermite(integrando, otimizador="BFGS", n.dim=1,
          n.pontos=1, f.fixo = y~1, dados=subset(dados, ID == 1), 
          beta.fixo = 2, prec.pars=4, log=TRUE))
## [1] -22.8
  ## 10 pontos
 log(adaptative.gauss.hermite(integrando, otimizador="BFGS", n.dim=1,
          n.pontos=10, f.fixo = y~1, dados=subset(dados, ID == 1), 
          beta.fixo = 2, prec.pars=4, log=TRUE))
## [1] -22.4
  ## 21 pontos
 log(adaptative.gauss.hermite(integrando, otimizador="BFGS", n.dim=1,
          n.pontos=21, f.fixo = y~1, dados=subset(dados, ID == 1),
          beta.fixo = 2, prec.pars=4, log=TRUE))
## [1] -22.4

Com isso, terminamos nossa explanação dos métodos baseados na ideia de aproximar o integrando por algum tipo de polinômio que seja de fácil integração, e usar este como uma aproximação para a verdadeira integral. Na sequência, vamos apresentar um método diferente baseado em simulação, a ideia implícita é estimar o valor da integral. Este procedimento recebe o nome de integração Monte Carlo, além do método básico vamos apresentar algumas variações como o método de Quase Monte Carlo e Quase Monte Carlo adaptativo.

6.3.5 Integração Monte Carlo

Integração Monte Carlo é um método simples e geral para aproximar integrais. Assuma que desejamos estimar o valor da integral de uma função \(f(x)\) em algum domínio \(D\) qualquer, ou seja, \[\begin{equation} I = \int_D f(x) dx \tag{6.12} \end{equation}\] A função não precisa ser unidimensional. De fato, técnicas Monte Carlo são muito usadas para resolver integrais de alta dimensão, além de integrais que não tem solução analítica, como no nosso caso.

Seja uma função densidade de probabilidade \(p(x)\) cujo domínio coincide com \(D\). Então, a integral em (6.12) é equivalente a \[ I = \int_D \frac{f(x)}{p(x)} p(x) dx . \] Essa integral corresponde a \(E\left( \frac{f(x)}{p(x)} \right)\), ou seja, o valor esperado de \(\frac{f(x)}{p(x)}\) com respeito a variável aleatória distribuída como \(p(x)\). Esta igualdade é verdadeira para qualquer função densidade de probabilidade em \(D\), desde que \(p(x) \neq 0\) sempre que \(f(x) \neq 0\).

Pode-se estimar o valor de \(E\left( \frac{f(x)}{p(x)} \right)\) gerando número aleatórios de acordo com \(p(x)\), calcular \(f(x)/p(x)\) para cada amostra, e calcular a média destes valores. Quanto mais amostras forem geradas, esta média converge para o verdadeiro valor da integral sendo este o princípio básico da integração Monte Carlo.

No caso específico de modelos de regressão com efeitos aleatórios, a grande maioria das integrais devem ser resolvidas nos reais, ou seja, precisamos de uma distribuição \(p(x)\) com este suporte. Escolhas naturais são as distribuições uniforme e gaussiana de dimensão igual a da integral a ser resolvida. Além disso, precisamos decidir a parametrização desta distribuição, ou seja, qual será seu vetor de média e sua matriz de variância/covariância. Em algoritmos básicos, o mais comum é usar o vetor de média como \(0\) e variância unitária. Mas, podemos adaptar este método de forma muito similar ao Gauss-Hermite adaptativo, espalhando os pontos pelo integrando de forma a cobrir melhor a região relevante de integração.

Além do espalhamento dos pontos, a geração dos pontos aleatórios também é um fator importante para este método. Como números aleatórios serão gerados a cada rodada do algoritmo, obtém-se diferentes valores para a integral o que é indesejável para maximização numérica. Uma abordagem alternativa são métodos Quase Monte Carlo, nos quais os números são gerados de acordo com uma sequência de baixa discrepância. Duas opções para a geração destas sequências de baixa discrepância, estão disponíveis no pacote fOptions, são elas Halton e Sobol. Afora esta escolha de pontos de baixa discrepâncias em substituição a aleatórios, o procedimento é o mesmo da integral de Monte Carlo.

Para exemplificar a ideia de integração Monte Carlo e Quase Monte Carlo, a função monte.carlo() implementa o método para uma função qualquer, e permite ao usuário escolher a forma de espalhamento dos pontos.

Código 6.15 Função para integração numérica por meio do método de Monte Carlo e Quasi Monte Carlo. 
require(fOptions)
monte.carlo <- function(funcao, n.dim, n.pontos, tipo, ...){
 if(tipo == "MC"){ pontos <- rmvnorm(n.pontos,mean=rep(0,n.dim))}
 if(tipo == "Halton"){ pontos <- rnorm.halton(n.pontos,n.dim)}
 if(tipo == "Sobol"){ pontos <- rnorm.sobol(n.pontos,n.dim)}
 norma <- apply(pontos,1,dmvnorm)
 integral <- mean(funcao(pontos,...)/norma)
 return(integral)
 }

Vamos resolver a integral contida no modelo Poisson com intercepto aleatório usando a função monte.carlo() com diferentes opções.

 log(monte.carlo(integrando, n.dim=1, tipo = "MC", n.pontos=20,
          f.fixo = y~1, dados=subset(dados, ID == 1), 
          beta.fixo = 2, prec.pars=4, log=FALSE))
## [1] -21.5
  log(monte.carlo(integrando, n.dim=1, tipo = "Sobol", n.pontos=20,
          f.fixo = y~1, dados=subset(dados, ID == 1), 
          beta.fixo = 2, prec.pars=4, log=FALSE))
## [1] -21.4

O mesmo problema na forma de espalhamento dos pontos encontrados no método de Quadratura de Gauss-Hermite, ocorre nos métodos de Monte Carlo e Quase Monte Carlo. Os pontos são sorteados de uma gaussiana de média \(0\) e variância \(1\), mas quando o integrando não for adequadamente coberto por estes pontos a integração será ruim. Podemos novamente adaptar os pontos de integração que agora são as amostras sorteadas, espalhando os pontos em volta de sua moda de acordo com o hessiano obtido no ponto modal, de modo a explorar melhor o integrando. O processo de adequação dos pontos é idêntico ao da adaptativa Gauss-Hermite, e não será detalhado novamente aqui. A função adaptative.monte.carlo() implementa este método para uma função qualquer.

Código 6.16 Função para integração numérica por meio do método de Monte Carlo Adaptativo e Quasi Monte Carlo Adaptativo. 
 adaptative.monte.carlo <- function(funcao, n.pontos, n.dim, 
                                    tipo, otimizador, ... ){
  pontos <- switch(tipo, 
                "MC" = {rmvnorm(n.pontos,mean=rep(0,n.dim))},
            "Halton" = {rnorm.halton(n.pontos, n.dim)},
            "Sobol" = {rnorm.sobol(n.pontos, n.dim)})
  integral <- -999999
  inicial <- rep(0,n.dim)
    temp <- try(optim(inicial, funcao, ... , method=otimizador,
                 hessian=TRUE,control=list(fnscale=-1)))
    if(class(temp) != "try-error"){
     z.chapeu <- temp$par
     H <- solve(-temp$hessian)
     sd.chapeu <- sqrt(diag(H))
     mat.nodes <- matrix(NA, ncol=n.dim,nrow=n.pontos)
     for(i in 1:length(z.chapeu)){
       mat.nodes[,i] <- z.chapeu[i] + sd.chapeu[i]*pontos[,i]
     }
  norma <- dmvnorm(mat.nodes,mean=z.chapeu,sigma=H,log=TRUE) 
  integral = mean(exp(funcao(mat.nodes,...) - norma))
    }
    return(integral)
 }

Novamente, vamos usar a função adaptative.monte.carlo() para resolver a integral contida no modelo Poisson com intercepto aleatório.

 log(adaptative.monte.carlo(integrando, n.dim=1, tipo="MC", 
          n.pontos=20, otimizador="BFGS", 
          f.fixo = y~1, dados=subset(dados, ID == 1), 
          beta.fixo = 2, prec.pars=4, log=TRUE))
## [1] -22.4
  log(adaptative.monte.carlo(integrando, n.dim=1, tipo="Halton", 
          n.pontos=20, otimizador="BFGS", 
          f.fixo = y~1, dados=subset(dados, ID == 1), 
          beta.fixo=2, prec.pars=4, log=TRUE))
## [1] -22.4
  log(adaptative.monte.carlo(integrando, n.dim=1, tipo="Sobol", 
          n.pontos=20, otimizador="BFGS", 
          f.fixo = y~1, dados=subset(dados, ID == 1), 
          beta.fixo=2, prec.pars=4, log=TRUE))
## [1] -22.4

Nesta Seção, revisamos diversos métodos de integração numérica e seu uso no R. Na sequência veremos alguns exemplos de modelos de regressão com efeitos aleatórios e como usar estes diversos métodos para a estimação por máxima verossimilhança.

6.4 Modelo Poisson com intercepto aleatório

Na seção 6.2.1 simulamos dados de um modelo Poisson com intercepto aleatório definido em (6.8). Agora vamos ver como usar os diversos métodos de integração numérica dentro do processo de estimação dos parâmetros \(\underline{\theta} = (\beta_0, \tau)\) deste modelo. O primeiro passo é escrever uma função com modelo completo como no código 6.17.

Código 6.17 Integrando da função de verossimilhança para o modelo de regressão de Poisson com efeito aleatório de intercepto. 
Poisson.Int <- function(b,beta.fixo, prec.pars, X, Z, Y,log=TRUE){
  tau <- exp(prec.pars)
  ll = sapply(b,function(bi){
    preditor <- as.matrix(X)%*%beta.fixo + as.matrix(Z)%*%bi
    lambda <- exp(preditor)
    sum(dpois(Y,lambda=lambda,log=TRUE)) + 
        dnorm(bi, 0, sd = 1/tau , log=TRUE)
  })
  if(log == FALSE){ll <- exp(ll)}
  return(ll)}

No código 6.18 definimos uma função genérica que capta um conjunto de dados e monta a log-verossimilhança, já integrada de acordo com uma das opções de integração apresentadas anteriormente. Essa função vai ser usada para diversos modelos com efeitos aleatórios apresentados neste texto.

Código 6.18 Função de verossimilhança genérica com opções de método de integração numérica. 
veroM <- function(modelo, formu.X, formu.Z, beta.fixo, prec.pars, 
                  integral, pontos, otimizador, n.dim, dados){
  dados.id <- split(dados, dados$ID)
  ll <- c()
  for(i in 1:length(dados.id)){
    X <- model.matrix(as.formula(formu.X),data=dados.id[[i]])
    Z <- model.matrix(as.formula(formu.Z),data=dados.id[[i]])
    if(integral == "LAPLACE"){
    ll[i] <- laplace(modelo,otimizador=otimizador,n.dim=n.dim, 
               X=X, Z=Z, Y=dados.id[[i]]$y, beta.fixo=beta.fixo,
               prec.pars=prec.pars,log=TRUE)}
    if(integral == "GH"){
    ll[i] <- gauss.hermite.multi(modelo, n.pontos= pontos, n.dim=n.dim, 
                    X=X, Z=Z, Y=dados.id[[i]]$y, beta.fixo=beta.fixo,
                    prec.pars=prec.pars,log=FALSE)}
    if(integral == "MC"){
    ll[i] <- monte.carlo(modelo,n.pontos=pontos, n.dim=n.dim, 
                   tipo= "MC", X=X, Z=Z, Y=dados.id[[i]]$y, 
                   beta.fixo=beta.fixo, prec.pars=prec.pars,
                   log=FALSE)}
    if(integral == "QMH"){
    ll[i] <- monte.carlo(modelo,n.pontos=pontos, n.dim=n.dim, 
                   tipo= "Halton", X=X, Z=Z, Y=dados.id[[i]]$y, 
                   beta.fixo=beta.fixo,
                   prec.pars=prec.pars,log=FALSE)}
    if(integral == "QMS"){
    ll[i] <- monte.carlo(modelo,n.pontos=pontos, n.dim=n.dim, 
                  tipo= "Sobol", X=X, Z=Z, Y=dados.id[[i]]$y, 
                  beta.fixo=beta.fixo, prec.pars=prec.pars,log=F)}
    if(integral == "AGH"){
    ll[i] <- adaptative.gauss.hermite(modelo,n.pontos=pontos, 
                  n.dim=n.dim, otimizador=otimizador,
                  X=X, Z=Z, Y=dados.id[[i]]$y, beta.fixo=beta.fixo,
                  prec.pars=prec.pars,log=TRUE)}
    if(integral == "AMC"){
    ll[i] <- adaptative.monte.carlo(modelo,n.pontos=pontos, 
                   n.dim=n.dim, otimizador=otimizador, tipo="MC",
                   X=X, Z=Z, Y=dados.id[[i]]$y, beta.fixo=beta.fixo,
                   prec.pars=prec.pars,log=TRUE)}
    if(integral == "AQMH"){
    ll[i] <- adaptative.monte.carlo(modelo,n.pontos=pontos, n.dim=n.dim, 
                 otimizador=otimizador, tipo="Halton", X=X, Z=Z, 
                 Y=dados.id[[i]]$y, beta.fixo=beta.fixo,
                 prec.pars=prec.pars,log=TRUE)}
    if(integral == "AQMS"){
    ll[i] <- adaptative.monte.carlo(modelo,n.pontos=pontos, n.dim=n.dim, 
                 otimizador=otimizador, tipo="Sobol", X=X, Z=Z, 
                 Y=dados.id[[i]]$y, beta.fixo=beta.fixo,
                 prec.pars=prec.pars,log=TRUE)}
    }
  return(sum(log(ll)))
}

A função veroM() foi definida de forma genérica. Alternativamente, pode-se definir uma função específica para cada modelo. Para o modelo Poisson com intercepto aleatório definimos o código 6.19.

Código 6.19 Função de verossimilhança marginal para o modelo de regressão de Poisson com efeito aleatório de intercepto. 
mod.Poisson <- function(b0,tau,integral, pontos, otimizador, 
                        n.dim, dados){
  ll = veroM(modelo = Poisson.Int, formu.X="~1", formu.Z="~1", 
             beta.fixo = b0, prec.pars=tau, integral=integral, 
             pontos=pontos,otim=otimizador,n.dim=n.dim,dados=dados)
  #print(round(c(b0,tau,ll),2))
  return(-ll)}

Usando a função mle2() para estimar os parâmetros via o algoritmo BFGS, e aproximação de Laplace, temos o seguinte.

system.time(P.laplace <- mle2(mod.Poisson,start=list(b0=0,tau=log(1/4)),
  data=list(integral="LAPLACE",otimizador = "BFGS", n.dim=1, 
  dados=dados, pontos=NA)))
##    user  system elapsed 
##    2.46    0.00    2.46
summary(P.laplace)
## Maximum likelihood estimation
## 
## Call:
## mle2(minuslogl = mod.Poisson, start = list(b0 = 0, tau = log(1/4)), 
##     data = list(integral = "LAPLACE", otimizador = "BFGS", n.dim = 1, 
##         dados = dados, pontos = NA))
## 
## Coefficients:
##     Estimate Std. Error z value   Pr(z)    
## b0    2.0070     0.0727   27.60 < 2e-16 ***
## tau   1.6207     0.2964    5.47 4.5e-08 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## -2 log L: 492

Para os demais métodos de integração obtemos os seguintes valores da log-verossimilhança:

par <- coef(P.laplace)
MET <- c("LAPLACE","GH","MC","QMH","QMS","AGH","AMC","AQMH","AQMS")
sapply(MET, function(metodo){
       mod.Poisson(b0=par[1],tau=par[2], integral=metodo,
                   pontos=21, n.dim=1,otimizador="BFGS", dados=dados)})
## LAPLACE      GH      MC     QMH     QMS     AGH     AMC    AQMH 
##     246     244     249     245     245     246     246     246 
##    AQMS 
##     246

Neste exemplo todos os métodos apresentaram valores muito próximos do obtido pela aproximação de Laplace, mais isto não significa que todos possuem o mesmo comportamento numérico. Por exemplo, o método Monte Carlo, requer muitos pontos para convergência, o que o torna muito lento pois a cada iteração estamos re-sorteando de uma gaussiana multivariada. Alternativamente e de forma mais eficiente, podemos sortear apenas uma vez e usar os mesmos pontos em todas as iterações do algoritmo numérico. O mesmo se aplicada a todos os outros métodos.

Para implementações mais eficientes devemos abandonar ou alterar a função genérica apresentada aqui apenas como exemplo didático. Algoritmos mais eficientes podem já receber os pontos de integração como argumento da função. Implementações análogas podem ser feitas para implementar a quadratura de Gauss-Hermite de forma mais eficiente. Ressaltamos que neste momento não estamos interessados em eficiência computacional, apenas em apresentar os aspectos gerais dos métodos de integração numérica.

O mesmo ajuste feito anteriormente utilizando Laplace fornece o resultado a seguir usando quadratura de Gauss-Hermite.

system.time(P.GH <- mle2(mod.Poisson,start=list(b0=0,tau=log(1/4)),
  data=list(integral="GH",pontos=100, n.dim=1, dados=dados)))
##    user  system elapsed 
##   6.513   0.004   6.521
summary(P.GH)
## Maximum likelihood estimation
## 
## Call:
## mle2(minuslogl = mod.Poisson, start = list(b0 = 0, tau = log(1/4)), 
##     data = list(integral = "GH", pontos = 100, n.dim = 1, dados = dados))
## 
## Coefficients:
##     Estimate Std. Error z value  Pr(z)    
## b0    2.0164     0.0734   27.47 <2e-16 ***
## tau   1.6356     0.2917    5.61  2e-08 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## -2 log L: 492

Repetimos ainda o ajuste com quasi-Monte Carlo com os pontos de Sobol. Neste exemplo, obtemos resultados semelhantes porém com tempos computacionais diferentes.

system.time(P.AQMS <- mle2(mod.Poisson,start=list(b0=0,tau=log(1/4)),
  data=list(integral="AQMS",pontos=10,otimizador="BFGS", 
  n.dim=1, dados=dados)))
##    user  system elapsed 
##    2.99    0.00    2.99
summary(P.AQMS)
## Maximum likelihood estimation
## 
## Call:
## mle2(minuslogl = mod.Poisson, start = list(b0 = 0, tau = log(1/4)), 
##     data = list(integral = "AQMS", pontos = 10, otimizador = "BFGS", 
##         n.dim = 1, dados = dados))
## 
## Coefficients:
##     Estimate Std. Error z value   Pr(z)    
## b0    2.0067     0.0726   27.62 < 2e-16 ***
## tau   1.6222     0.2966    5.47 4.5e-08 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## -2 log L: 492

Com isso, passamos por todas as etapas do processo de estimação de um modelo de regressão com efeitos aleatórios ilustrando os princípios básicos e fundamentos dos algoritmos. Na sequência, vamos discutir alguns modelos com mais elementos, como por exemplo, com diferentes estruturas de efeitos aleatórios. O processo de especificação/implementação do modelo e os métodos de integração seguem os mesmos princípios vistos até aqui. Nos próximos exemplos, mudamos a matriz \(Z\) de delineamento associada aos efeitos aleatórios.

6.5 Poisson com efeito aninhado

Considere o experimento, onde \(i\) unidades amostrais são divididas em \(j\) blocos e dentro de cada bloco são realizadas \(k\) repetições. A Figura 6.4 ilustra este delineamento amostral.

Estrutura de um delineamento com efeito aninhado.

Figura 6.4: Estrutura de um delineamento com efeito aninhado.

Suponha que a variável de interesse segue um modelo de Poisson. Então um modelo adequado para este tipo de experimento é:

\[\begin{align*} & Y_{ijk} \sim P(\lambda_{ijk}) \\ & g(\lambda_{ijk}) = (\beta_0 + b_i) + b_{i:j} \\ & b_i \sim N(0, \sigma^2) \;\; ; \;\; b_{i:j} \sim N(0,\tau^2) \end{align*}\] onde \(i = 1, \ldots , N\) é o número de unidades amostrais envolvidas no experimento que no caso da Figura~ possui \(N = 5\). O índice \(j = 1,\ldots, n_i\) identifica os blocos dentro de cada unidade amostral e \(k=1, \ldots, n_{ij}\) é o número de repetições dentro de cada grupo em cada unidade amostral. Note que este modelo tem três parâmetros \(\underline{\theta} = (\beta_0, \sigma^2, \tau^2)\).

Para este exemplo vamos simular um conjunto de dados seguindo esta estrutura. Vamos fixar o número de unidades amostrais em \(N = 4\), vamos dividir cada unidade em \(n_i = 5\) blocos e dentro de cada bloco realizar \(n_{ij}=4\) observações. A função rpois.ani() simula dados deste modelo. A Figure 6.5 ilustra a estrutura do experimento.

Código 6.20 Função para simular do modelo de regressão Poisson com efeitos aleatórios aninhados sobre o intercepto. 
rpois.ani <- function(N, ni, nij, beta.fixo, prec.pars){
  ua <- as.factor(rep(1:nij,each=N*ni))
  bloco <-rep(as.factor(rep(1:ni,each=nij)),N)
  rep <- rep(as.factor(rep(1:nij,ni)),N)
  dados <- data.frame(ua,bloco,rep)
  dados$Bloco.A <- interaction(ua,bloco)
  Z1 <- model.matrix(~ ua - 1,data=dados)
  Z2 <- model.matrix(~Bloco.A -1, data=dados)
  X <- model.matrix(~1, data=dados)
  n.ua <- ncol(Z1)
  n.bloco <- ncol(Z2)
  b.ua <- rnorm(n.ua,0,sd=1/prec.pars[1])
  b.bloco <- rnorm(n.bloco, sd=1/prec.pars[2])
  Z <- cbind(Z1,Z2)
  XZ <- cbind(X,Z)
  beta <- c(beta.fixo,b.ua,b.bloco)
  preditor <- XZ%*%beta
  lambda <- exp(preditor)
  y <- rpois(length(lambda),lambda=lambda)
  dados$y <- y
  names(dados) <- c("ID","bloco","rep","Bloco.A","y")
  return(dados)
}

Para simular do modelo precisamos fixar o vetor de parâmetros, vamos usar \(\beta_0 = 3\), \(\sigma = 1\) e \(\tau = 2\). A seguinte chamada da função realiza a simulação e retorna um conjunto de dados, no formato adequado para ser utilizado posteriormente no processo de inferência.

set.seed(123)
dados <- rpois.ani(N = 4, ni = 5, nij = 4, beta.fixo = 3, 
                   prec.pars=c(2,2))
head(dados)
##   ID bloco rep Bloco.A  y
## 1  1     1   1     1.1 13
## 2  1     1   2     1.1 15
## 3  1     1   3     1.1 11
## 4  1     1   4     1.1 11
## 5  1     2   1     1.2  9
## 6  1     2   2     1.2  6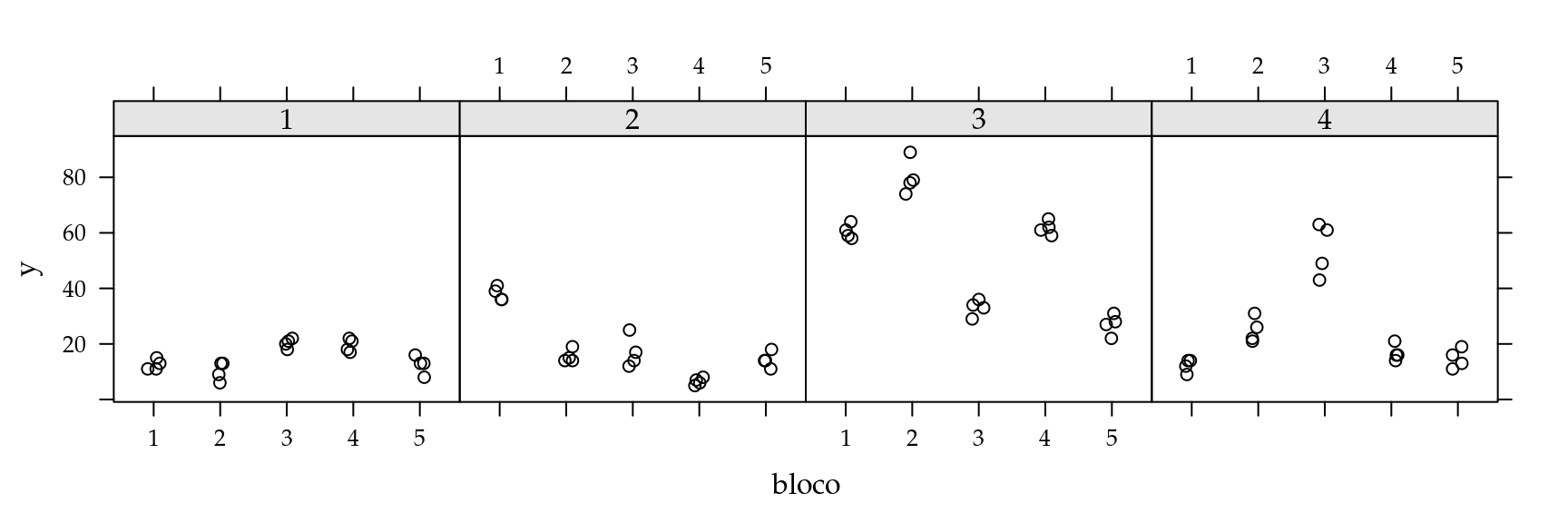
Análise descritiva modelo com efeito aninhado.

Figura 6.5: Análise descritiva modelo com efeito aninhado.

A seguir escrevemos uma função com a estrutura do modelo.

Código 6.21 Integrando da função de verossimilhança para o modelo de regressão de Poisson com efeito aleatório aninhado sobre o intercepto. 
Poisson.Ani <- function(b, beta.fixo, prec.pars,X, Z, Y,log=TRUE){
  sigma <- exp(prec.pars[1]) 
  tau <- exp(prec.pars[2])
  preditor <- as.matrix(X)%*%beta.fixo + as.matrix(Z)%*%b
  lambda <- exp(preditor)
  ll =  sum(dpois(Y,lambda=lambda,log=TRUE)) + 
            dnorm(b[1], 0, sd = 1/sigma , log=TRUE) + 
            sum(dnorm(b[2:6], 0, sd = 1/tau , log=TRUE))
  if(log == FALSE){ll <- exp(ll)}
  return(ll)}

Note a reparametrização feita nos parâmetros de variância, onde vamos estimá-los em escala logarítmica. Esta transformação muda o espaço de busca do algoritmo numérico dos reais positivos para todo os reais, o que ajuda no processo de otimização. Além disso, observe a complexidade deste modelo: para cada unidade amostral temos \(6\) desvios aleatórios, um pela própria unidade amostral e mais \(5\) um para cada bloco dentro da unidade amostral. Isso impacta fortemente no método de integração a ser escolhido para resolver a integral contida na função de verossimilhança. Por exemplo, pelo método de Gauss-Hermite, suponha que escolhemos \(21\) pontos de integração em seis dimensões implica que a cada interação do algoritmo de maximização numérica precisamos avaliar a função \(21^6 = 85766121\) vezes, o que é inviável. Nestas situações apenas a aproximação de Laplace ainda é aplicável, e será usada neste problema. Veja também que com apenas \(4\) unidades amostrais, devemos estimar \(4 + 4*5 = 24\) efeitos aleatórios no total. A função vero.Poisson.Ani() apresenta uma versão simplificada da função veroM() do código 6.18 para o caso do Modelo Poisson com efeito aninhado usando apenas a integração por Laplace.

Código 6.22 Função de verossimilhança para o modelo de regressão de Poisson com efeito aleatório aninhado sobre o intercepto. 
vero.Poisson.Ani <- function(modelo, formu.X, formu.Z, beta.fixo, 
                             prec.pars,otimizador, dados){
 dados.id <- split(dados, dados$ID)
 ll <- c()
 for(i in 1:length(dados.id)){
    X <- model.matrix(as.formula(formu.X),data=dados.id[[i]])
    Z <- model.matrix(as.formula(formu.Z),data=dados.id[[i]])
    ll[i] <- laplace(modelo,otimizador=otimizador,n.dim=ncol(Z), 
                     X=X, Z=Z , Y=dados.id[[i]]$y, 
                     beta.fixo=beta.fixo,
                     prec.pars=prec.pars,log=TRUE)
  }
  return(sum(log(ll)))
}

Escrevemos o modelo no formato adequado para ser usado dentro da função mle2().

Código 6.23 Função de log-verossimilhança marginal para o modelo de regressão de Poisson com efeito aleatório aninhado sobre o intercepto. 
mod.Poisson.Ani <- function(b0,sigma,tau, otimizador,formu.X, 
                            formu.Z,  dados){
ll = vero.Poisson.Ani(modelo = Poisson.Ani, formu.X = formu.X, 
                      formu.Z = formu.Z, beta.fixo = b0, 
                      prec.pars=c(sigma,tau),
                      otimizador=otimizador,dados=dados)
  #print(round(c(b0,sigma,tau,ll),2))
  return(-ll)}

O processo de otimização da função de log-verossimilhança marginalizada pela função mle2().

require(bbmle)
dados$UM <- 1
ini <- c(log(mean(dados$y)), log(sd(dados$y))/2)
Poisson.Aninhado = mle2(mod.Poisson.Ani,
                        start=list(b0= ini[1],sigma=ini[2],tau= ini[2]),
                        method="BFGS",control=list(lmm=3, reltol=1e-5),
                        data=list(formu.X="~1", formu.Z="~UM+bloco-1", 
                        otimizador = "BFGS",dados=dados))
summary(Poisson.Aninhado)
## Maximum likelihood estimation
## 
## Call:
## mle2(minuslogl = mod.Poisson.Ani, start = list(b0 = ini[1], sigma = ini[2], 
##     tau = ini[2]), method = "BFGS", data = list(formu.X = "~1", 
##     formu.Z = "~UM+bloco-1", otimizador = "BFGS", dados = dados), 
##     control = list(lmm = 3, reltol = 1e-05))
## 
## Coefficients:
##       Estimate Std. Error z value   Pr(z)    
## b0       3.088      0.239   12.92 < 2e-16 ***
## sigma    0.866      0.434    2.00 0.04603 *  
## tau      0.694      0.186    3.73 0.00019 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## -2 log L: 555

Dada a reparametrização dos parâmetros de variância, precisamos retorná-los para escala original. De acordo com a propriedade de invariância dos estimadores de máxima verossimilhança, para as estimativas pontuais basta aplicar a transformação inversa, ou seja,

exp(coef(Poisson.Aninhado)[2:3])
## sigma   tau 
##  2.38  2.00

verifica-se que os valores estimados estão bastante próximos dos verdadeiros valores dos parâmetros utilizados na simulação. Para a construção de intervalos de confiança para o parâmetro \(\beta_0\) basta usar os resultados assintóticos e construir o intervalo de confiança usando o erro padrão fornecido junto ao \(summary()\) do modelo, ou então,

confint(Poisson.Aninhado, method="quad")
##        2.5 % 97.5 %
## b0    2.6199   3.56
## sigma 0.0153   1.72
## tau   0.3289   1.06

note que a saída acima apresenta os intervalos de confiança para os parâmetros de variância reparametrizados. Se desejarmos obter intervalos aproximados para os parâmetros de variância na escala original não podemos apenas aplicar a transformação inversa. Para isto, precisamos utilizar os resultados apresentados nos Teoremas \(4\) e \(5\). Aplicando estes resultados temos,

Vcov <- vcov(Poisson.Aninhado)
sd.sigma <- sqrt(exp(coef(Poisson.Aninhado)[2])^2*Vcov[2,2])
sd.tau <- sqrt(exp(coef(Poisson.Aninhado)[3])^2*Vcov[3,3])
ic.sigma = exp(coef(Poisson.Aninhado)[2]) + c(-1,1)*qnorm(0.975)*sd.sigma
ic.tau = exp(coef(Poisson.Aninhado)[3]) + c(-1,1)*qnorm(0.975)*sd.tau
ic.sigma
## [1] 0.355 4.398
ic.tau
## [1] 1.27 2.73

os intervalos de confiança obtidos via aproximação quadrática parecem muito curtos. Isso pode ser devido a uma pobre aproximação do Hessiano numérico, utilizado para calcular os erros padrões assintóticos, ou a aproximação quadrática é muito ruim nesta situação, apresentando erros padrões extremamente otimistas.

Para investigar a primeira possibilidade, podemos recalcular o Hessiano numérico pelo método de Richardson especifico para aproximar numericamente a derivada segunda de uma função qualquer. Este método está implementado na função hessian() do pacote numDeriv. Para usar a função hessian(), precisamos reescrever a função de verossimilhança, passando os parâmetros em forma de vetor.

mod.Poisson.Ani.Hessian <- function(par, dados){
  saida <- mod.Poisson.Ani(b0=par[1], sigma = par[2], tau = par[3], 
                           otimizador="BFGS", formu.X = "~1", 
                           formu.Z = "~UM + bloco - 1", dados=dados)
  return(saida)
}

Reescrita a função queremos avaliar o Hessiano no ponto de máximo, ou seja, a matriz de informação observada.

Io <- numDeriv::hessian(mod.Poisson.Ani.Hessian, x = coef(Poisson.Aninhado), 
              method="Richardson", dados=dados)

Podemos comparar o inverso da matriz de informação observada, pelo algoritmo e o obtido fora pelo método de Richardson.

Vcov         ## Anterior
##             b0    sigma       tau
## b0    0.057136  0.00335  0.000647
## sigma 0.003351  0.18827 -0.008248
## tau   0.000647 -0.00825  0.034664
solve(Io)    ## Richardson
##          [,1]     [,2]      [,3]
## [1,] 0.057136  0.00335  0.000647
## [2,] 0.003351  0.18827 -0.008248
## [3,] 0.000647 -0.00825  0.034664

É possível ver claramente que pelo método de Richardson as variância são maiores, levando a maior confiança dos resultados. Podemos novamente construir os intervalos de confiança agora com os novos desvios padrões, inclusive para o parâmetro de média \(\beta_0\).

Vcov.H <- solve(Io)
ic.b0 <- coef(Poisson.Aninhado)[1] + c(-1,1)*sqrt(Vcov.H[1,1])
sd.sigma.H <- sqrt(exp(coef(Poisson.Aninhado)[2])^2*Vcov.H[2,2])
sd.tau.H <- sqrt(exp(coef(Poisson.Aninhado)[3])^2*Vcov.H[3,3])
ic.sigma.H = exp(coef(Poisson.Aninhado)[2]) + 
                 c(-1,1)*qnorm(0.975)*sd.sigma.H
ic.tau.H = exp(coef(Poisson.Aninhado)[3]) + 
               c(-1,1)*qnorm(0.975)*sd.tau.H
ic.b0
## [1] 2.85 3.33
ic.sigma.H
## [1] 0.355 4.398
ic.tau.H
## [1] 1.27 2.73

Com os erros padrões corrigidos os intervalos de confiança ficaram mais largos, e mais coerentes com o que esperamos, nos dois casos o verdadeiro valor dos parâmetros estão contidos nos intervalos. Uma outra opção, muito mais cara computacionalmente é obter os intervalos baseados em perfil de verossimilhança.

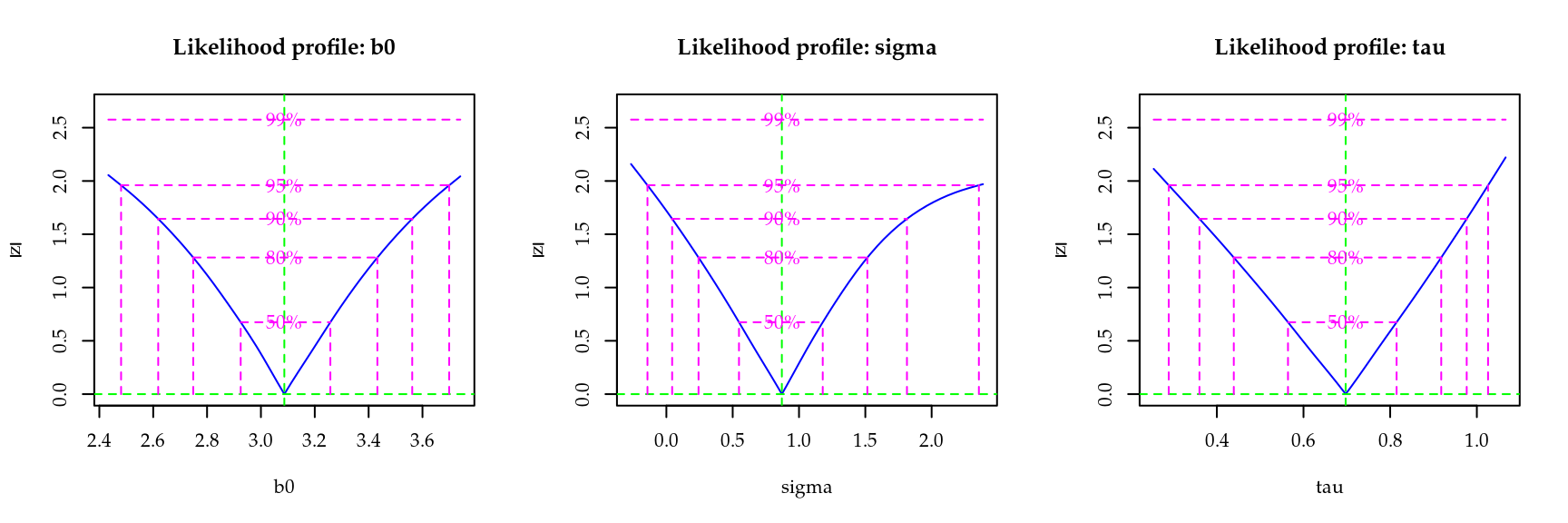
Perfil de verossimilhança - Modelo Poisson com efeito aninhado.

Figura 6.6: Perfil de verossimilhança - Modelo Poisson com efeito aninhado.

Podemos comparar os intervalos perfilhados com os obtidos pela aproximação quadrática.

perfil.b0 <- confint(perfil)[1,]
perfil.sigma <- exp(confint(perfil)[2,])
perfil.tau <- exp(confint(perfil)[3,])
ic = cbind(rbind(ic.b0,perfil.b0),
          rbind(ic.sigma.H,perfil.sigma),
          rbind(ic.tau.H,perfil.tau))
ic
##           2.5 % 97.5 % 2.5 % 97.5 % 2.5 % 97.5 %
## ic.b0      2.85   3.33 0.355    4.4  1.27   2.73
## perfil.b0  2.48   3.70 0.867   10.5  1.33   2.79

Os resultados mostram que a aproximação quadrática, tende a apresentar intervalos mais curtos que os de verossimilhança perfilhada. O parâmetro que parece sofrer mais com este efeito é o \(\sigma\). Com isso, concluímos o processo de inferência do modelo Poisson com efeito aninhado.

6.6 Modelo Beta longitudinal

Considere a situação onde uma variável resposta \(Y_{it}\) restrita ao intervalo unitário, é observada em \(i=1, \ldots, N\) unidades amostrais, em \(t=1, \ldots, n_i\) tempos. A natureza da variável aleatória indica que a distribuição Beta é uma candidata natural para descrever os dados. Um possível modelo para esta situação é o seguinte: \[\begin{align*} Y_{it} &\sim B(\mu_{it}, \phi) \\ g(\mu_{it}) &= (\beta_0 + b_i) + (\beta_1 + b_1)t \\ \begin{bmatrix} b_0\\ b_1 \end{bmatrix} &\sim NM_2 \left ( \begin{bmatrix} 0\\ 0 \end{bmatrix}, \begin{bmatrix} \sigma_I^2 & \rho\\ \rho & \sigma_S^2 \end{bmatrix} \right ) \end{align*}\]

A principal diferença deste modelo para os anteriores é que não supomos independência entre os efeitos aleatórios. Neste caso, temos um modelo com intercepto e inclinação aleatória e adicionamos um parâmetro de correlação entre os efeitos. Para completar a especificação precisamos da função \(g(\cdot)\) que liga o preditor a esperança da Beta que definimos pela função como a logit. A função rbeta.model() simula uma realização deste modelo.

Código 6.24 Função para simular variáveis aleatórias do modelo de regressão Beta longitudinal. 
inv.logit <- function(x){exp(x)/(1+exp(x))}
rbeta.model <- function(ID, tempo, beta.fixo, prec.pars){
  dados = data.frame("ID" = rep(1:ID,each=tempo), 
          "cov" = rep(seq(0, 1,l=tempo),ID))
  dados.id <- split(dados,dados$ID)
  cov.rho <- prec.pars[3]*sqrt(prec.pars[1])*sqrt(prec.pars[2])
  Sigma<-matrix(c(prec.pars[1],cov.rho,cov.rho,prec.pars[2]),2,2)
  y <- matrix(NA, ncol=ID, nrow=tempo)
  for(i in 1:ID){
    X <- model.matrix(~cov, data=dados.id[[i]])
    Z <- model.matrix(~cov, data=dados.id[[i]])
    b <- rmvnorm(n=1,mean=c(0,0),sigma=Sigma)
    preditor <- X%*%as.numeric(beta.fixo) + Z%*%as.numeric(b)
    mu <- inv.logit(preditor)
    y[,i]<-rbeta(length(mu),mu*prec.pars[4],
                 (1-mu)*prec.pars[4])
  }
  dados$y <- c(y)
  return(dados)
}

O modelo Beta tem vetor de parâmetros \(\underline{\theta} = (\beta_0, \beta_1, \sigma_I, \sigma_S, \rho, \phi)\). São dois parâmetros de média e quatro de variabilidade, sendo três deles associados à gaussiana bivariada atribuída aos efeitos aleatórios, além do parâmetro de dispersão da Beta. A Figura 6.7 apresenta um gráfico das trajetórias simuladas para cada unidade amostral ao longo do tempo.
Para simulação usamos uma chamada da função rbeta.model() do código (6.24).

Trajetórias por unidade amostral - Modelo Beta longitudinal.

Figura 6.7: Trajetórias por unidade amostral - Modelo Beta longitudinal.

Escrever este modelo em R requer cuidado com os parâmetros de variância envolvidos. Todos os parâmetros de variância/dispersão foram reparametrizados, para serem estimados em escala logarítmica. Para o parâmetro de correlação \(\rho\), que assume valores no intervalo \((-1,1)\), utilizamos a transformação logística.

Código 6.25 Integração da função de log-verossimilhança para o modelo de regressão Beta logitudinal. 
transf.rho <- function(rho){
  -1+2*(exp(rho)/(exp(rho)+1))
}
vero.slope <- function(uv,beta.fixo, prec.pars, X, Z, Y,log=TRUE){
  sigmaI <- exp(prec.pars[1])^2
  sigmaS <- exp(prec.pars[2])^2
  rho <- transf.rho(prec.pars[3])
  phi <- exp(prec.pars[4])
  cov.rho <- rho*(sqrt(sigmaI)*sqrt(sigmaS))
  if(class(dim(uv)) == "NULL"){uv <- matrix(uv,1,2)}
  ll = apply(uv,1,function(uvi){
    preditor <- X%*%beta.fixo + Z%*%as.numeric(uvi)
    mu <- inv.logit(preditor)
    sigma <- matrix(c(sigmaI,cov.rho,cov.rho,sigmaS),2,2)
    sum(dbeta(Y, mu*phi, (1-mu)*phi, log=TRUE)) + 
        dmvnorm(uvi, c(0,0), sigma = sigma , log=TRUE)})
  if(log == FALSE){ll <- exp(ll)}
  return(ll)}

Usando a função veroM() definida no código 6.18, podemos colocar o modelo da forma apropriada para utilizar a função mle2().

Código 6.26 Função de log-verossimilhança marginal para o modelo de regressão Beta longitudinal. 
model.Beta <- function(b0,b1,sigmaI,sigmaS,rho, phi, otimizador, 
                       n.dim, dados){
 ll = veroM(modelo = vero.slope, formu.X="~cov",
            formu.Z="~cov", beta.fixo = c(b0,b1), 
            prec.pars=c(sigmaI,sigmaS,rho,phi), 
            integral=integral, pontos=pontos, 
            otimizador=otimizador, n.dim=n.dim,dados=dados)
  #print(round(c(b0,b1,sigmaI, sigmaS, rho, phi, ll),2))
  return(-ll)}

Com o modelo no formato adequado podemos proceder com a inferência realizando o ajuste com uma chamada da função mle2().

ajuste = mle2(model.Beta, start=list(b0=0, b1=0,sigmaI=-0.5, 
             sigmaS=-0.5, rho = 0.3, phi = log(25)), method="BFGS", 
             data=list(integral="LAPLACE", pontos=1, otimizador="BFGS", 
             n.dim=2,dados=dados))
summary(ajuste)
## Maximum likelihood estimation
## 
## Call:
## mle2(minuslogl = model.Beta, start = list(b0 = 0, b1 = 0, sigmaI = -0.5, 
##     sigmaS = -0.5, rho = 0.3, phi = log(25)), method = "BFGS", 
##     data = list(integral = "LAPLACE", pontos = 1, otimizador = "BFGS", 
##         n.dim = 2, dados = dados))
## 
## Coefficients:
##        Estimate Std. Error z value   Pr(z)    
## b0        0.717      0.197    3.65 0.00026 ***
## b1        0.991      0.188    5.27 1.4e-07 ***
## sigmaI   -0.528      0.247   -2.14 0.03226 *  
## sigmaS   -0.743      0.346   -2.15 0.03187 *  
## rho       1.299      1.105    1.18 0.23972    
## phi       3.546      0.124   28.69 < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## -2 log L: -335

Os intervalos de confiança podem ser obtidos na escala reparametrizada. Usamos os resultados dos Teoremas ?? e ?? para obter intervalos aproximados na escala original dos parâmetros.

confint(ajuste, method="quad")
##         2.5 %  97.5 %
## b0      0.332  1.1023
## b1      0.623  1.3597
## sigmaI -1.012 -0.0447
## sigmaS -1.421 -0.0644
## rho    -0.867  3.4656
## phi     3.304  3.7884

Outra forma alternativa é obter intervalos baseados em perfil de verossimilhança, que em geral apresentam resultados melhores, porém são computacionalmente mais “caros” (demorados). Por outro lado, a transformação para escala original é simples aplicando-se diretamente a função de reparametrização aos limites do intervalo. Isto é justificado pela propriedade de invariância da verossimilhança. A Figura 6.8 apresenta os perfis de verossimilhança dos parâmetros do modelo Beta longitudinal.

Perfil de verossimilhança - Modelo Beta longitudinal.

Figura 6.8: Perfil de verossimilhança - Modelo Beta longitudinal.

6.7 Modelo linear dinâmico

Os modelos dinâmicos são uma classe de modelos de regressão usualmente aplicados a séries temporais. Nesses modelos, os coeficientes de regressão variam no tempo. A evolução dos coeficientes é parametrizada de forma a ser suave e dinâmica, originando esse nome. O modelo dinâmico mais simples é o modelo com apenas um intercepto, \[\begin{eqnarray} y_t & = & \theta_t + v_t,\;\;\; v_t \sim N(0, V) \nonumber \\ \theta_t - \mu & = & \phi (\theta_{t-1}-\mu) + w_t, \;\;\; w_t \sim N(0, W) \tag{6.13} \end{eqnarray}\] em que \(V\), \(W\) e \(\phi\) são parâmetros de variância, \(\mu\) é a média do intercepto \(\theta_t\).

O maior interesse é a modelagem de \(\theta_t\), considerando sua estrutura de evolução e de erro. Pode-se considerar que \(\theta_t\) é um estado latente (não observável) subjacente ao que se observa. Desta forma, os modelos dinâmicos também são chamados de modelos de espaço de estados.

Nesse modelo \(V\) mede o erro das observações; \(\mu\) está associada à média de \(y\), \(\phi\) e \(W\) controlam a suavidade da evolução de \(\theta_t\). Com \(0 \leq \phi \leq 1\) temos um modelo autoregressivo de ordem 1 para \(\theta\). Com \(\phi=1\) temos um passeio aleatório para \(\theta\) e \(y\) é um passeio aleatório mais um ruído. Com \(\phi=1\) e \(W\) pequeno em relação a \(V\), \(y_t\) será parecido com \(y_{t-1}\). West and Harrison (1997) e Petris, Petrone, and Campagnoli (2009) apresentam mais detalhes e estruturas mais gerais de modelos dinâmicos. Uma generalização da expressão acima é dada por

\[\begin{eqnarray} y_t & = & F_t \theta_t + v_t \nonumber \\ (\theta_t - \mu) & = & G_t (\theta_t - \mu) + w_t . \tag{6.14} \end{eqnarray}\]

Aqui, vamos considerar essa especificação geral no contexto de regressão dinâmica. Então, nomeamos os elementos da seguinte forma:

  • \(y_t\) vetor resposta de dimensão \(m\),

  • \(F_t\) pode ser uma matriz de covariáveis,

  • \(\theta_t\) vetor de coeficientes de regressão,

  • \(v_t\) vetor de erros das observações, \(v_t \sim N(0, V_t)\),

  • \(\mu\) média dos coeficientes de regressão,

  • \(w_t\) vetor de erros dos estados, \(w_t \sim N(0, W_t)\),

  • \(G_t\) matriz de evolução dos estados.

São feitas as seguintes suposições de independência condicional: \[\begin{align*} [y_t | y_{0:t}, \theta_{0:t}] &= [y_t|\theta_t] \\ [\theta_t | \theta_{0:t}, y_{0:t}] &= [\theta_t|\theta_{t-1}] . \end{align*}\] Para o modelo linear gaussiano, temos \[\begin{align*} [y_t|\theta_t] &= N(F_t\theta_t, V_t) \\ [\theta_t|y] &= N(G_t\theta_t, W_t) . \end{align*}\]

É comum considerar que \(V_t = V\), \(W_t = W\) e \(G_t = G\), isto é, constantes no tempo. Notemos que, além dessas condições, com \(G=I\) e \(w_t=0\) para todo \(t\), temos um modelo de regressão linear usual.

6.7.1 Filtro de Kalman e verossimilhança

Vamos considerar que \(\psi_t\) = \(\{V_t, W_t, G_t\}\) é o conjunto de parâmetros desconhecidos. Também, vamos considerar que \(\psi_t = \psi\), ou seja, os parâmetros são fixos no tempo. Podemos estimar \(\psi\) via máxima verossimilhança. A verossimilhança para os modelos lineares dinâmicos leva em conta que \[ [Y] = [Y_1] [Y_2|Y_1] \ldots [Y_n|Y_{n-1}, \ldots,Y_1]. \] Considerando, \(v_t\) um erro gaussiano, \([y_t|\ldots]\) também é gaussiano. Para obter a verossimilhança, basta conhecer as médias e variâncias condicionais de \([y_t|\ldots]\), que dependem de \(\psi\) (Schweppe (1965)). O filtro de Kalman (Kalman (1960)) fornece um algoritmo para o cálculo dessas médias e variâncias condicionais. Portanto, o filtro de Kalman pode ser usado para calcular a verossimilhança, que é o produto dessas densidades condicionais. Esta abordagem é explorada por diversos autores como,
por exemplo, Akaike (1978), Harvey and Phillips (1979), Jones (1980), Gardner, Harvey, and Phillips (1980) e Harvey (1981).

O filtro de Kalman, foi proposto originalmente para correção e filtragem de sinais eletrônicos. Nesse contexto, considera-se que o estado latente é o verdadeiro sinal e o que se observa é o sinal mais um ruído. Este algoritmo esta baseado na distribuição condicional de \(y_t\) e \(\theta_t\), obtidas, respectivamente, num passo de filtragem e num passo de suavização. Assim, o primeiro passo é usado para calcular a verossimilhança e o segundo para fazer inferência sobre \(\theta_t\).

Na filtragem, usam-se as equações para a predição de \(\theta_t\), isto é, \(\theta_t|\theta_{t-1} = \theta_t^{t-1}\) e para obter \(\theta_t\) filtrado: \(\theta_t^t\). Também, obtêm-se \(P_t^{t-1}\) e \(P_t^t\), que é, respectivamente, \(P_t\) predito e filtrado. E na suavização obtêm-se \(\theta_t^n\) e \(P_t^n\), que são estimativas da média e variância de \(\theta_t\).

As equações de predição, para \(t=1,2,\ldots,n\), são: \[\begin{eqnarray} \theta_t^{t-1} & = & G \theta_{t-1}^{t-1}\\ P_t^{t-1} & = & G P_{t-1}^{t-1} G^{'} + W \tag{6.15} \end{eqnarray}\] com \(\theta_0^0=\mu_0\) e \(P_0^0 = C_0\). \(\mu_0\) e \(C_0\) são, respectivamente, a média e a variância de \(\theta_0\). Para considerações sobre \(\mu_0\) e \(C_0\) ver De Jong (1988).

As equações de filtragem, para \(t=1,2,\ldots,n\), são: \[\begin{eqnarray*} e_t & = & y_t - F_t \theta_t^{t-1} \\ Q_t & = & F_t P_t^{t-1} F_t^{'} + V \\ K_t & = & P_t^{t-1} F_t^{'} Q_t^{-1} \\\ \theta_t^t & = & \theta_t^{t-1} + K_t e_t \\ P_t^t & = & P_t^{t-1} - K_t F_t P_t^{t-1} \tag{6.16} \end{eqnarray*}\]

Na suavização, obtém-se os valores suavizados de \(\theta_t\), isto é, \(\theta_t^n=\hat{\theta}\), a estimativa de \(\theta_t\). Também, obtêm-se \(P_t^n\), o valor suavizado de \(P_t\). \(P_t^n\) quantifica a incerteza de \(\hat{\theta_t}\). Inicialmente, para \(t=n\) têm-se: \(\theta_{n}^{n} = \theta_{t}^{t}\), \(P_n^n = P_t^t\), apenas para \(t=n\)
Para \(t=n, n-1, \ldots, 1\), têm-se: \[\begin{eqnarray} J_{t-1} & = & P_{t-1}^{t-1} G^{'} (P_t^{t-1})^{-1} \\ \theta_{t-1}^n & = & \theta_{t-1}^{t-1} + J_{t-1} (\theta_t^n - \theta_t^{t-1}) \\ P_{t-1}^n & = & P_{t-1}^{t-1} + J_{t-1} (P_t^n - P_t^{t-1})J_{t-1}^{'} \tag{6.17} \end{eqnarray}\]

Com \(e_t\) e \(Q_t\) obtidos no passo de filtragem do filtro de Kalman e considerando que ambos dependem de \(\psi\), temos \[\begin{equation} l(\psi) = -\frac{1}{2}\sum_{t=1}^n{\log | Q_t |} -\frac{1}{2}\sum_{t=1}^n{e_t^{'} Q_t^{-1}e_t} . \tag{6.18} \end{equation}\]

6.7.2 Um exemplo simples

Vamos considerar o caso mais simples, descrito no início desta seção, considerando \(\mu=0\). Neste caso, temos um intercepto que evolui dinamicamente. São três os parâmetros deste modelo: variância do erro das observações, variância do erro dos estados e parâmetro de evolução dos estados. Inicialmente, vamos simular um conjunto de dados.

n <- 100
V <- .2; W <- .3; rho <- 0.9
set.seed(1)
w <- rnorm(n, 0, sqrt(W))
v <- rnorm(n, 0, sqrt(V))
x <- w[1]
for (i in 2:n)
  x[i] <- rho*x[i-1] + w[i]
y <- x + v

Vamos definir uma função que crie uma lista em R contendo: (i) as informações básicas sobre a dimensão da série \(n\), \(m\) e \(k\), (ii) elementos \(y\), \(F\), \(x\), \(V\), \(W\) e \(G\), que representam os componentes do modelo \(y_t\), \(F_t\), \(\theta_t\), \(V\), \(W\) e \(G\), respectivamente. Além disso, essa lista também incluirá os elementos \(x.p\), \(x.f\), \(x.s\), \(P.p\), \(P.f\) e \(P.s\), para representar os estados e variâncias preditos, filtrados e suavizados, respectivamente; e os elementos \(e\) e \(Q\), para representar os elementos usados no cálculo da verossimilhança. Também, armazenamos os elementos m0 e c0, para representar \(\mu_0\) e \(C_0\).

Esta função é particular para este exemplo, com \(V\), \(G\) e \(W\) escalares:

Código 6.27 Estrutura para o modelo com intercepto dinâmico. 
ddlm1 <- function(y, G, V, W, m0=0, c0=1e5) { 
  ## y: vetor de dados 
  ## G: coeficiente autoregressivo 
  ## V: variância dos erros de observação 
  ## W: variância dos erros do estado 
  ## m0, c0: media e variância de theta.0
  dlm <- mget(ls(), environment()) ## lista com argumentos
  n <- length(y)
  dlm[c("n","F","e","S")] <- list(n,rep(1,n),rep(0,n),rep(V,n))
  dlm[c("x.s", "x.f", "x.p")] <- rep(list(rep(m0, n+1)), 3)
  dlm[c("P.s", "P.f", "P.p")] <- rep(list(rep(W,  n+1)), 3)
  ## retorna uma lista (nomeada) com argumentos e os elementos:
  ## n: tamanho da serie
  ## F: vetor de 1's
  ### elementos predefinidos para armazenar resultados: 
  ## x.p, x.f e x.s; P.p, P.f, P.s e P.t; e, S 
  return(dlm)
}

Usando essa função para criar a estrutura de modelo dinâmico para os dados simulados

mod1 <- ddlm1(y, 0, 100, 100)

Agora, definimos uma função para a filtragem específica para este exemplo, com \(V\), \(G\) e \(W\) escalares:

Código 6.28 Filtragem para o modelo dinâmico simples: intercepto dinâmico. 
kfilter1 <- function(dlm) {
  ## dlm: saída de funcao ddlm1() com componentes do modelo
  for (i in 1:dlm$n+1) {
    dlm <- within(dlm, {
      x.p[i] <- G*x.f[i-1]
      P.p[i] <- G*P.f[i-1]*t(G) + W
      e[i-1] <- y[i-1] - F[i-1]*x.p[i]
      S[i-1] <- F[i-1]*P.p[i]*F[i-1] + V
      K <- (P.p[i]*F[i-1])/S[i-1]
      x.f[i] <- x.p[i] + K*e[i-1]
      P.f[i] <- P.p[i] - K*F[i-1]*P.p[i]
    })
  }
  ## retorna objeto lista com valores atualizados dos
  ## componentes x.p, P.p e, S, x.f e P.f definidos em dlm1()
  return(dlm[1:16])
}

Considerando que temos \(y_t\) univariado, a função para calcular o negativo da log-verossimilhança pode ser simplesmente:

nlldlm1 <- function(dlm) -sum(dnorm(dlm$e, 0.0, sqrt(dlm$S), log=TRUE))

A maximização da função de verossimilhança pode ser feita usando a função optim(). Vamos definir, então, uma função que recebe os parâmetros de interesse e retorna o negativo da log-verossimilhança do modelo.

Código 6.29 Função de verossimilhança do modelo com intercepto dinâmico. 
opfun1 <- function(pars, dlm) {
  ## pars: vetor valores dos três parâmetros do modelo simples
  ## dlm: objeto com componentes do modelo simples
  dlm[c("V", "W", "G")] <- pars  
  dlm <- kfilter1(dlm)
  return(nlldlm1(dlm))
}

Agora, vamos definir iniciais e usar a função optim() para encontrar as estimativas. Vamos usar o método L-BFGS-B que considera restrição no espaço paramétrico definida pelos argumentos lower e upper.

op1 <- optim(c(1,1,.5), opfun1, dlm=mod1, 
             hessian=TRUE, method="L-BFGS-B",
             lower=rep(1e-7,3), upper=c(Inf, Inf, 1))
op1$par                     # estimativas
## [1] 0.171 0.315 0.824
sqrt(diag(solve(op1$hess))) # erros padrão
## [1] 0.0864 0.1245 0.0791

Com a estimativa desses parâmetros, podemos obter a estimativa de \(\theta_t\). Para isso, precisamos implementar também o passo de suavização. Vamos definir uma função para isso.

Código 6.30 Suavização para o modelo com intercepto dinâmico. 
ksmooth1 <- function(dlm) { 
  ## dlm: lista com componentes do modelo dinamico simples, 
  ##      suavizada com a funcao kfilter1(). 
  dlm <- within(dlm, {
    x.s[n+1] <- x.f[n+1] 
    P.s[n+1] <- P.f[n+1]
  })
  for (i in dlm$n:2) { 
    J <- with(dlm, P.f[i]*G/P.p[i+1])
    dlm <- within(dlm, {
      x.s[i] <- x.f[i] + J*(x.s[i+1]-x.p[i+1])
      P.s[i] <- P.f[i] + J*(P.s[i+1]-P.p[i+1])*J })
  }
  return(dlm) # retorna componentes x.s e P.s atualizados 

}

Definindo a série com os valores estimados, aplicamos o filtro e a suavização à série filtrada.

fit1 <- ddlm1(y, op1$par[3], op1$par[1], op1$par[2])
fit1f <- kfilter1(fit1)
fit1s <- ksmooth1(fit1f)

Em R a estimação via máxima verossimilhança pode ser feita utilizando o pacote dlm (Petris, Petrone, and Campagnoli (2009)). O pacote é voltado para estimação bayesiana. É possível obter estimativas de máxima verossimilhança, considerando-se que a matriz \(G\) é conhecida. Para ilustração fazemos uma comparação dos resultados obtidos e com resultados obtidos com o pacote dlm. Neste caso, vamos considerar \(G=1\).

require(dlm)
### define função para criar objeto dlm a 
### partir do vetor de parâmetros do modelo
m.build <- function(pars) {
  ## pars: vetor de três parâmetros do modelo simples 
  m <- dlmModPoly(1, dV=pars[1], dW=pars[2])
  m["GG"] <- pars[3]
  ## retorna objeto dlm com parâmetros dV, dW e GG 
  ## alterados 
  m
}
y.mle <- dlmMLE(y, rep(1,3), m.build, hessian=TRUE, 
                lower=rep(1e-7, 3), upper=c(Inf, Inf, 1))
## compara estimativas obtidas pelas funções definidas 
## com as estimativas obtidas pelas funções do pacote 'dlm'
## estimativas:
rbind(op1$par, y.mle$par)
##       [,1]  [,2]  [,3]
## [1,] 0.171 0.315 0.824
## [2,] 0.171 0.315 0.823
## erros padrão:
round(rbind(sqrt(diag(solve(op1$hess))), 
            sqrt(diag(solve(y.mle$hess)))), 4)
##        [,1]  [,2]   [,3]
## [1,] 0.0864 0.124 0.0791
## [2,] 0.0865 0.125 0.0792
### monta modelo com estimativas obtidas
y.mod <- m.build(y.mle$par)
### filtragem e suavização
y.filt <- dlmFilter(y, y.mod)
y.smoo <- dlmSmooth(y.filt)
### extrai erros dos estados 
xm.se <- sqrt(unlist(dlmSvd2var(y.smoo$U.S, y.smoo$D.S)))

Na Figura 6.9 podemos visualizar os valores de \(\theta_t\) simulados e estimados pelas funções que definimos e as do pacote dlm.

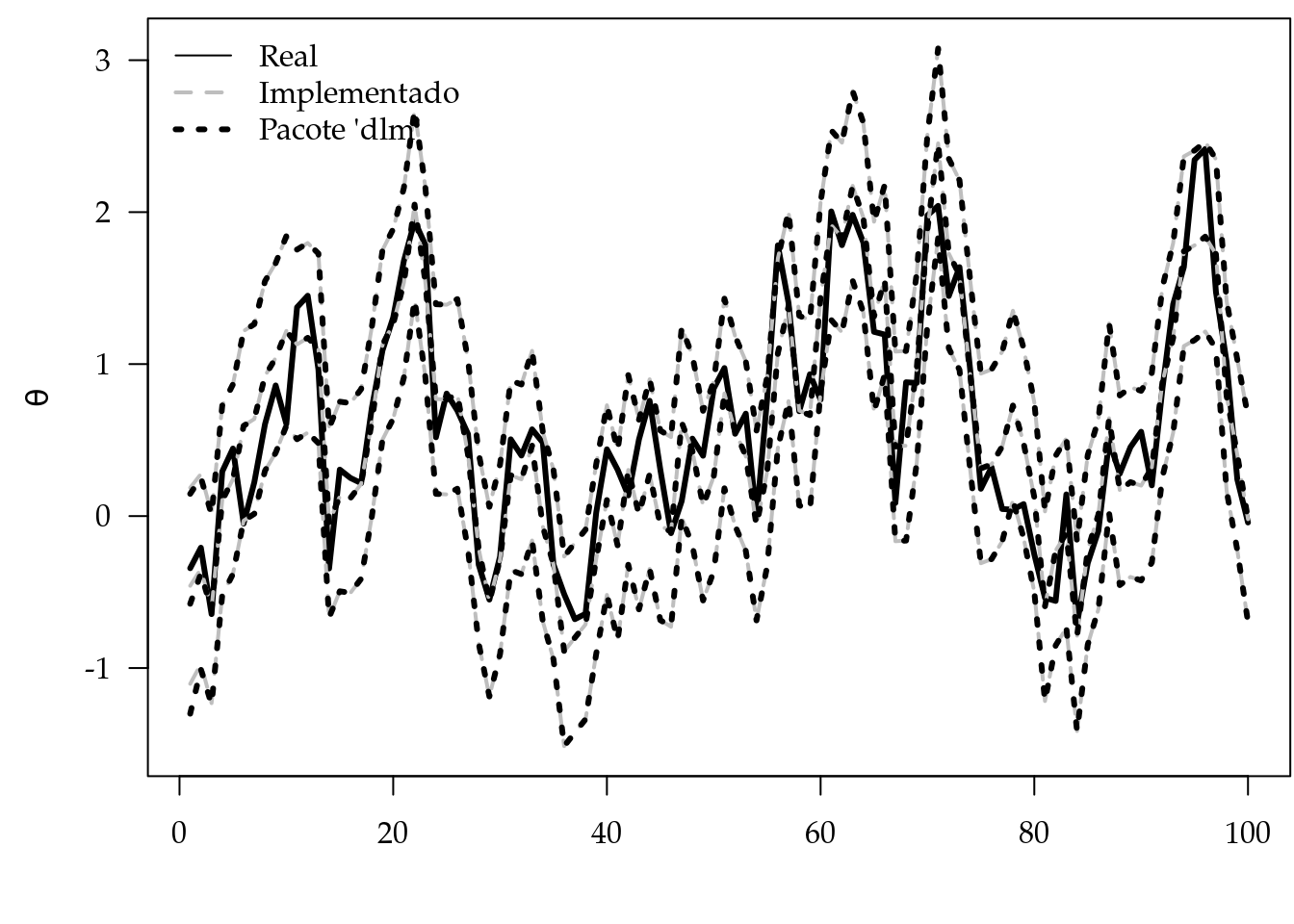
Estado latente simulado e estimado e respectivos intervalos de confiança obtidos pelas funções implementadas e as do pacote dlm.

Figura 6.9: Estado latente simulado e estimado e respectivos intervalos de confiança obtidos pelas funções implementadas e as do pacote dlm.

6.7.3 Exemplo de regressão dinâmica

Vamos agora considerar um modelo dinâmico de regressão com uma covariável. Neste exemplo, as equações de filtragem são bastante simplificadas. Nesse modelo, temos como parâmetros: a variância das observações \(V\), a variância \(W\) de \(w_t\) e a matriz \(G\). Vamos considerar \(W\) e \(G\) diagonais. Portanto, temos cinco parâmetros a serem estimados.

Inicialmente, vamos simular um conjunto de dados que contém agora uma covariável.

n <- 100    # define tamanho da série
set.seed(1) # simula covariável
x <- rbind(1, 3*runif(n), rexp(n,1))  
W <- diag(c(0.3, 0.2, 0.1))
### simula erros dos estados 
w <- rbind(rnorm(n, 0, sqrt(W[1,1])),
           rnorm(n, 0, sqrt(W[2,2])), 
           rnorm(n, 0, sqrt(W[3,3])))
V <- 0.1 # variância do erro nas observações 
v <- rnorm(n, 0, sqrt(V)) # erro nas observações 
G <- diag(c(0.7, 0.8, 0.9)) # matriz de evolução dos estados 
### simula estados e observações 
theta <- matrix(NA, nrow(W), n)
theta[,1] <- w[,1]
y <- rep(NA, n)
y[1] <- x[,1]%*%theta[,1] + v[1]
for (i in 2:n) {
  theta[,i] <- G%*%theta[,i-1] + w[,i]
  y[i] <- x[,i]%*%theta[,i] + v[i]
}

Vamos definir no código 6.31 uma função que crie uma lista contendo as componentes do modelo. Esta lista é semelhante à criada no exemplo anterior, porém, para o contexto de regressão dinâmica. No código 6.32 definimos uma função para a filtragem.

Código 6.31 Estrutura para o modelo de regressão dinâmica. 
ddlm1r <- function(y, F, G, V, W, 
             m0=rep(0,ncol(W)), V0=diag(ncol(W))*1000) {
  ## y: vetor de dados , F: matriz de covariaveis
  ## G: matriz diagonal com coeficientes autoregressivos 
  ## V: variância dos erros de observação 
  ## W: matriz diagonal de variância dos erros dos estados 
  ## m0 e c0: vetor media e matrix variancia de theta.0
  dlm <- mget(ls(), environment())
  n=length(y)  ;  k=nrow(W)
  dlm[c("n", "k")] <- c(n, k)
  dlm[c("x.s","x.f","x.p")] <- rep(list(matrix(m0, k, n+1)), 3)
  dlm[c("P.s","P.f","P.p")] <- rep(list(array(V0,c(dim(W),n+1))),3)
  dlm[c("e", "S")] <- list(rep(0, n), rep(V, n))
  ## retorna uma lista com os adicionais elementos:
  ## n: tamanho da serie ;  k: dimensão dos estados 
  ## e elementos predefinidos armazenar resultados 
  return(dlm)
}
Código 6.32 Filtragem para o modelo de regressão dinâmica. 
kfilter1r <- function(dlm) { 
  ## dlm: lista criada com funcao ddlm1r()
  for (i in 1:dlm$n+1) {
    dlm <- within(dlm, {
      x.p[,i] <- G%*%x.f[,i-1]
      aux <- tcrossprod(P.f[,,i-1], G)
      P.p[,,i] <- G%*%aux + W
      e[i-1] <- y[i-1] - F[,i-1]%*%x.p[,i]
      aux <- crossprod(P.p[,,i], F[,i-1])
      S[i-1] <- F[,i-1]%*%aux + V
      K <- (P.p[,,i]%*%F[,i-1])/S[i-1]
      x.f[,i] <- x.p[,i] + K*e[i-1]
      aux <- K%*%F[,i-1]
      P.f[,,i] <- P.p[,,i] - aux%*%P.p[,,i]
    })
  }
  ## retorna objeto lista com valores atualizados dos
  ## componentes x.p, P.p e, S, x.f e P.f definidos em dlm1r()
  return(dlm[1:17])
}

Considerando que temos \(y_t\) univariado, a função para calcular o negativo da log-verossimilhança é a mesma do exemplo anterior. Precisamos, apenas, definir outra função que recebe os parâmetros de interesse e retorna o negativo da log-verossimilhança do modelo.

Código 6.33 Função dos parâmetros do modelo de regressão dinâmica para minimizar. 
opfun1r <- function(pars, dlm) {
  ## pars: vetor com 2*k + 1 parâmetros 
  ## dlm: lista com componentes do modelo de regressao 
  ##     dinamica (k=numero de covariaveis/estados)
  k <- (length(pars)-1)/2
  dlm[c("V", "W", "G")] <- 
      list(pars[1], diag(pars[1+1:k]), diag(pars[1+k+1:k]))
  dlm <- kfilter1r(dlm)
  return(nlldlm1(dlm))
}

Agora, vamos considerar valores iniciais e usar a função optim() para encontrar as estimativas.

mod1r <- ddlm1r(y=y, F=x, G=0.5*diag(3), V=1, W=diag(3))
op1r <- optim(rep(.5, 7), opfun1r, dlm=mod1r, method="L-BFGS-B",
              lower=rep(1e-5,7), upper=rep(c(Inf, 1), c(4,3)), 
              hessian=TRUE)
### estimativas obtidas 
round(op1r$par, 4)
## [1] 0.163 0.160 0.197 0.110 0.803 0.644 0.803
### calculando os erros padroes das estimativas 
round(sqrt(diag(solve(op1r$hess))), 4)
## [1] 0.1481 0.1873 0.0633 0.0727 0.1787 0.1200 0.1105

Agora, precisamos implementar a suavização. Neste caso, observando as equações (6.17), observamos que, quando \(\theta_t\) é vetor (\(W\) é matriz), temos que fazer a conta \(P_{t-1}^{t-1}G^{'}(P_t^{t-1})^{-1}\) em cada passo. Aqui é bom considerar que essa matriz é simétrica para ter um ganho computacional. Uma opção para isso, é fazer a decomposição de Choleski, que é uma matriz triangular, e fazer a inversão dessa matriz, considerando sua estrutura. Em R usamos chol2inv(chol(M)), para inverter uma matriz quadrada simétrica e positiva definida M.

Outra consideração sobre contas matriciais é sobre o cálculo de A'B. Em R é mais rápido fazer crossprod(A, B) que fazer simplesmente |t(A) %*% B| para esse cálculo. Porém, se precisamos calcular AB (sem transpor qualquer das duas matrizes), é melhor usar |A %*% B| que usar crossprod(t(A),B), se as matrizes são de dimensões pequenas. Desta forma, definimos a função no código 6.34.

Código 6.34 Suavização para o modelo de regressão dinâmica. 
ksmooth1r <- function(dlm) {
  ## dlm: lista com componentes do modelo de regressão dinâmica. 
  ##      suavizada com a funcao kfilter1r().
  dlm <- within(dlm, {
    x.s[,n+1] <- x.f[,n+1]
    P.s[,,n+1] <- P.f[,,n+1]
  })
  for (i in dlm$n:1) {
    dlm <- within(dlm, {
      aux <- crossprod(G,chol2inv(chol(P.p[,,i+1])))
      J <- P.f[,,i]%*%aux
      x.s[,i] <- x.f[,i] + J%*%(x.s[,i+1]-x.p[,i+1]) 
      aux <- tcrossprod(P.s[,,i+1]-P.p[,,i+1], J)
      P.s[,,i] <- P.f[,,i] + J%*%aux
    })
  }
  ## retorna objeto lista com valores atualizados dos
  ## componentes x.s e P.s definidos em dlm1r()
  return(dlm[1:17])
}

Definindo a série com os valores estimados

fit1r <- ddlm1r(y, x, diag(op1r$par[5:7]), op1r$par[1],
                diag(op1r$par[2:4]))

Aplicando o filtro e a suavização à série filtrada.

kf1r <- kfilter1r(fit1r)
ks1r <- ksmooth1r(kf1r)

Extraindo a variância dos estados (diagonal de \(P_t^n\)), para facilitar o cálculo e visualização dos intervalos de confiança para \(\theta_t\):

th.se <- sqrt(apply(ks1r$P.s[,,-1], 3, diag))

Vamos implementar o mesmo modelo usando funções do pacote dlm.

k <- nrow(x)
mr.bf <- function(pars) {
  ## pars: vetor de 2*k+1 parametros do modelo regressao 
  ##     dinamica (k=numero de covariaveis/estados)
  m <- dlmModReg(t(x[-1,]), dV=pars[1], dW=pars[1+1:k])
  m$GG <- diag(pars[1+k+1:k])
  ## retorna objeto dlm com dV, dW e GG atualizados 
  m
}
opd1r <- dlmMLE(y, rep(1, 1+2*k), mr.bf, 
                lower=rep(1e-7, 1+2*k), hessian=TRUE)
### estimativas:
round(rbind(op1r$par, opd1r$par), 4)
##       [,1]  [,2]  [,3] [,4]  [,5]  [,6]  [,7]
## [1,] 0.163 0.160 0.197 0.11 0.803 0.644 0.803
## [2,] 0.161 0.164 0.197 0.11 0.799 0.641 0.802
### erros padrões 
round(rbind(sqrt(diag(solve(op1r$hess))), 
            sqrt(diag(solve(opd1r$hess)))), 4)
##       [,1]  [,2]   [,3]   [,4]  [,5]  [,6]  [,7]
## [1,] 0.148 0.187 0.0633 0.0727 0.179 0.120 0.111
## [2,] 0.151 0.193 0.0635 0.0730 0.182 0.123 0.111
### monta modelo com estimativas obtidas
modd1r <- mr.bf(opd1r$par)
### filtragem e  suavização
kfd1r <- dlmFilter(y, modd1r)
ksd1r <- dlmSmooth(kfd1r)
### extrai erros dos estados 
xm.se1r <- sqrt(sapply(dlmSvd2var(ksd1r$U.S, ksd1r$D.S), diag))

Notamos algumas diferenças nos valores das estimativas e respectivos erros padrões. As funções do pacote dlm usam a decomposição em valores singulares em vez da decomposição de Choleski. Na Figura 6.10, podemos visualizar \(\theta_t\) simulados e estimados:

Coeficientes de regressão simulados, e estimados (e respectivos intervalos de confiança) via funções implementadas e via funções do pacote 'dlm'.

Figura 6.10: Coeficientes de regressão simulados, e estimados (e respectivos intervalos de confiança) via funções implementadas e via funções do pacote ‘dlm.’

Na estimação de \(\theta_t\), e sua variância, em ambos os exemplos de modelos dinâmicos, foi considerado a estimativa de máxima verossimilhança de \(\psi\) obtida. Ou seja, não está sendo considerada a incerteza dessa estimativa na inferência sobre \(\theta_t\). Uma opção para isso é considerar um método baseado no algoritmo EM, no qual \(\psi\) e \(\theta\) são estimados conjuntamente. Nos complementos online deste livro acrescentaremos exemplos com essa abordagem.

Uma solução natural para esse tipo de problema é a abordagem de inferência bayesiana. Essa abordagem é bastante comum na literatura de modelos dinâmicos. Isto será ilustrado em versões futuras deste material.