Chapter 4 Exemplos não convencionais
4.1 Modelo autoregressivo de ordem 1
Nos exemplos do Capítulo 3 consideramos observações independentes e a verossimilhança é portanto dada pelo produto das densidades. Vamos considerar agora um modelo simples, porém com observações não independentes. Tomamos o caso de um modelo AR1 (autoregressivo de ordem 1) para dados gaussianos que é um modelo básico em séries temporais. Um texto de referência na área é Clélia M. C. Toloi (2004). Vamos considerar uma versão simplificada deste modelo assumindo que o processo possui média zero e variância unitária. Desta forma, o modelo é definido por:
\[\begin{align} y_{t+1} &= \rho y_t + e_{t+1} \\ \nonumber e_t &\sim N(0, \sigma^2=1) \\ \nonumber \mbox{com } & |\rho| < 1 \end{align}\]
Decorre deste modelo que \[\begin{align*} [Y_i|Y_{i-1}] &\sim N(\rho \, y[i-1], 1) \;\; ; \;\; i = 2, \ldots, n \;, \\ [Y_1] &\sim N(0, 1/(1-\rho^2)) \;\; ; \;\; i = 2, \ldots , n. \end{align*}\]
Uma simulação da série fixando os valores necessários é feita com os comandos a seguir. Definimos o valor do parâmetro \(\rho = 0,7\) e o número de observações \(n = 100\). A série simulada é mostrada na Figura 4.1.
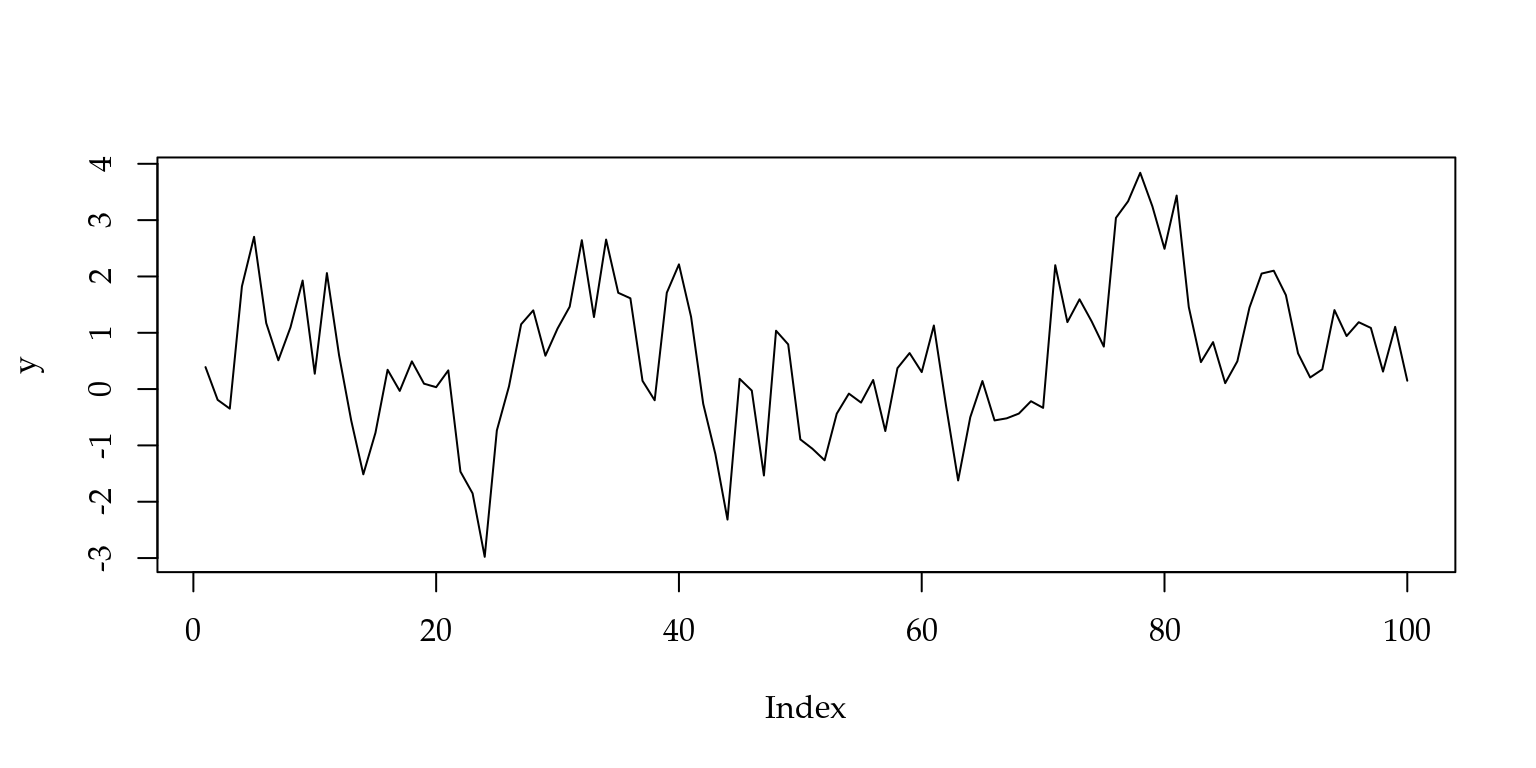
Figura 4.1: Valores da série simulada - Modelo AR1.
A expressão da função de verossimilhança é equivalente à distribuição conjunta para as \(n\) observações, uma distribuição gaussiana multivariada neste caso. Vamos explorar aqui algumas formas alternativas de escrever esta função.
Podemos escrever a distribuição conjunta com a expressão da distribuição multivariada gaussiana de \([Y_1, Y_2, \ldots, Y_n]\) induzida pelo modelo ou pelo produto das distribuições condicionais univariadas. No caso do modelo AR1 as distribuições univariadas dependem apenas da observação anterior e temos então que a expressão da verossimilhança é:
\[\begin{align} \mathrm{L}(\rho) &\equiv [Y_1, Y_2, \ldots, Y_n] = [Y_1] [Y_2|Y_1] \ldots [Y_n|Y_{n-1}] = [Y_1] \prod_{i=2}^n [Y_i|Y_{i-1}]. \tag{4.1} \end{align}\]
Uma verosimilhança aproximada é obtida ignorando-se a contribuição da primeira observação, ou seja pela distribuição condicional à primeira observação,
\[\begin{equation} \mathrm{L_A}(\rho) = \prod_{i=2}^n [Y_i|Y_{i-1}]. \tag{4.2} \end{equation}\]
Neste caso é possível encontrar o estimador do parâmetro em forma fechada com \(\mathrm{L_A}(\rho)\) mas métodos numéricos são necessários para maximizar \(\mathrm{L}(\rho)\).
Entretanto, no que se segue vamos sempre utilizar métodos numéricos uma vez que o foco aqui não é discutir este modelo em particular mas sim ilustrar implementações que possam ser adaptadas para modelos que possuam estrutura similar.
Começamos definindo no código 4.1 a função de verossimilhança aproximada.
Por conveniência definimos também uma versão vetorizada da função o que pode ser feito facilmente usando a função Vectorize(). Vetorizar a função é é útil para processar diversos valores do parâmetro de uma só vez como, por exemplo, quando fazemos gráficos da função.
llAR1.a <- function(par, sigma=1, dados) {
n <- length(dados)
ll <- sum(dnorm(dados[2:n], mean=par*dados[1:(n-1)],
sd=sigma, log=TRUE))
return(ll)
}
llAR1.a.V <- Vectorize(llAR1.a, "par")Com o comando a seguir obtém-se, por algorítimos numéricos, a estimativa do parâmetro \(\rho\) que maximiza a função de verossimilhança aproximada.
unlist(rho.est.a <- optimize(llAR1.a, int=c(0, 1), dados=y, maximum=TRUE))## maximum objective
## 0.727 -137.608(rho.a <- rho.est.a$maximum)## [1] 0.727No código 4.2 a seguir definimos a verossimilhança completa que inclui a distribuição da primeira observação que neste caso é convenientemente especificada como, \[ [Y_1] \sim N(0, 1/(1-\rho^2)) . \]
llAR1 <- function(par, sigma = 1, dados){
n <- length(dados)
ll <- dnorm(dados[1], mean=0, sd=sigma*sqrt(1/(1-par^2)), log=TRUE) +
sum(dnorm(dados[2:n],mean=par*dados[1:(n-1)],sd=sigma,log=TRUE))
}
llAR1.V <- Vectorize(llAR1, "par")Com esta função obtemos uma estimativa que, neste caso, é bem próxima à obtida com a verossimilhança aproximada.
unlist(rho.est <- optimize(llAR1, c(0,1), dados=y, maximum=TRUE))## maximum objective
## 0.72 -138.93(rho.emv <- rho.est$maximum)## [1] 0.72A seguir vamos traçar os gráficos das funções de verossimilhança. Inicialmente vamos definir uma função deviance genérica no sentido de que pode ser calculada dada uma verossimilhança.
devfun <- function(par, llfun, est, ...)
2*(llfun(est, ...) - llfun(par, ...))Os gráficos das funções de verossimilhança e deviance aproximadas e completas para os
dados simulados são mostrados na Figura 4.2. Para a primeira consideramos valores em todo o espaço paramétrico enquanto que para segunda tomamos apenas valores ao
redor da estimativa de máxima verossimilhança (completa). O intervalo de confiança foi definido aqui pela faixa de valores para \(\rho\) cuja verossimilhança seja de ao menos
10% da verosimilhança maximizada (\(r=0,10\)). Para isto encontramos o valor de corte correspondente na função deviance \(cD = -2 \log(r) = 4,605\) e usamos a função uniroot.all() do pacote rootSolve para encontrar os limites do intervalo.
require(rootSolve)
ICdev <- function(par, devfun, cD, ...) devfun(par, ...) - cD
(IC.rel10 <- uniroot.all(ICdev, c(0,1), devfun=devfun, cD=-2*log(0.1),
llfun=llAR1.V, est=rho.emv, dados=y))## [1] 0.569 0.869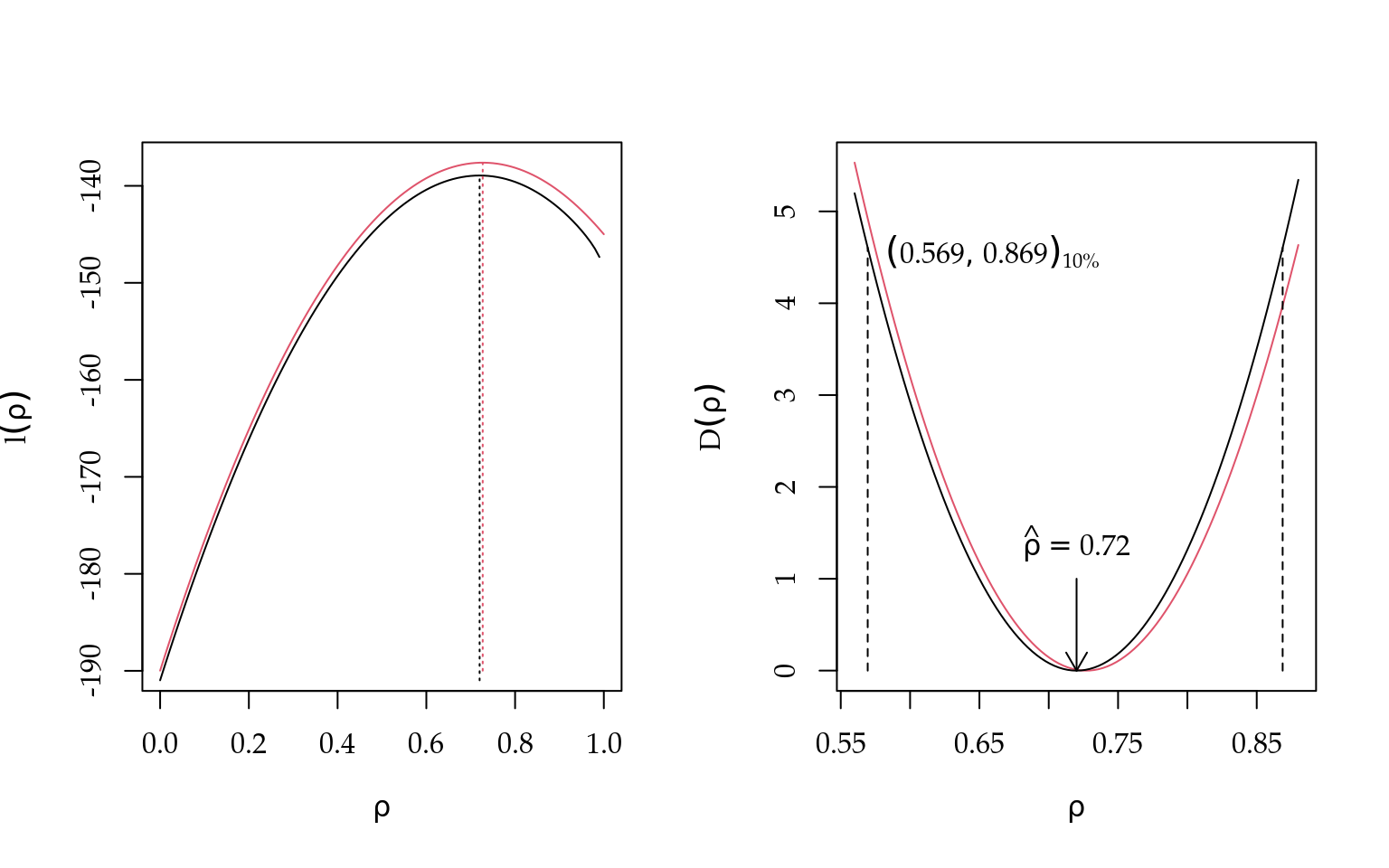
Figura 4.2: Função de verossimilhança (esquerda) e deviance (direita) aproximada (vermelha) e completa (preta) com estimativas pontual e intervalar do parâmetro rho para os dados simulados do modelo AR1.
Em implementações que visam eficiência a função llAR1() pode ser reescrita evitando o uso de dnorm() e utilizando as expressões das densidades escritas em função de estatísticas suficientes. Isto reduz o tempo computacional em procedimentos interativos e/ou que avaliam a função muitas vezes.
Passamos agora a outra forma de escrever a verossimilhança utilizando a expressão da densidade conjunta (multivariada).
\[\begin{equation} [Y_1, \ldots, Y_N] \sim N(0, \Sigma), \tag{4.3} \end{equation}\] em que os elementos de \(\Sigma\) são \(\Sigma_{ij} = \rho^{|i-j|}(1/(1-\rho^2))\). Os elementos da matriz são portanto função da distância \(|i-j|\) entre as observações. No comando a seguir ilustramos como montar esta matriz calculando as distâncias entre pares de pontos e depois calculando os valores para \(\rho=0,70\).
n <- length(y)
{S <- diag(n) ; S <- abs(row(S)-col(S))}
S <- 0.7^S * (1/(1-0.7^2))A expressão da log-verossimilhança é obtida pela densidade da distribuição gaussiana multivariada, sendo então:
\[\begin{equation} \mathrm{l}(\boldsymbol{\theta}) = \mathrm{l}(\sigma, \rho) = -\frac{n}{2}\log(2\pi) - \frac{1}{2}\log(|\Sigma|) - \exp\{\frac{1}{2}y\prime \Sigma^{-1}y\}. \tag{4.4} \end{equation}\]
Os três comandos a seguir mostram diferentes formas de avaliar esta densidade que produzem os mesmos resultados porém com tempos de execução distintos. Para ilustrar comparamos os tempos de execução de 100 avaliações destas funções. Os valores dos tempos não são relevantes e podem variar de um computador para outro. O relevante aqui é a comparação dos tempos, por exemplo tomando suas razões.
system.time(replicate(100, mvtnorm::dmvnorm(y,rep(0,n),S,log=T)))## user system elapsed
## 0.059 0.000 0.058system.time(replicate(100, (-n/2) * log(2*pi) -
determinant(S,log=T)$mod/2 - 0.5*mahalanobis(y,center=0,cov=S)))## user system elapsed
## 0.165 0.000 0.165system.time(replicate(100, {Schol <- chol(S);
(-n/2) * log(2*pi) - sum(log(diag(Schol))) -
0.5*crossprod(backsolve(Schol, y, transpose=T))}))## user system elapsed
## 0.036 0.000 0.037O custo computacional é determinado pelas operações que envolvem a matriz de covariância. A primeira estratégia utiliza a implementação do pacote mvtnorm. A segunda estratégia é a mais lenta pois acaba fazendo contas redundantes no cálculo do determinante e da forma quadrática \(y^{\prime}\Sigma^{-1} y\). A terceira estratégia é a mais eficiente pois tem o custo associado ao cálculo da decomposição de Choleski de \(\Sigma\) que, uma vez calculado, é usado para calcular de forma computacionalmente barata tanto o determinante quanto a forma quadrática. Estas diferenças podem ser muito relevantes em modelos que possuem alguma estrutura de covariância quando avalia-se a função de log-verossimilhança muitas vezes, como algoritmos de maximização ou de inferência por simulação. As diferenças serão maiores com o aumento do número de observações.
Para o caso considerado aqui, ganhos adicionais de tempo computacional ainda podem ser obtidos. Em certos casos, resultados analíticos podem ser usados ao escrever as funções. No modelo AR1 considerado aqui a matriz \(\Sigma\) tem inversa de forma conhecida e o código pode ser escrito de forma mais eficiente evitando a inversão da matriz ou a solução de sistemas lineares. Os elementos de \(\Sigma^{-1}\) são:
\[ \left\{ \begin{array}{ll} \Sigma^{-1}_{i,i} = 1 & \mbox{ para } i=1 \mbox{ e } i=n \\ \Sigma^{-1}_{i,i} = 1+\rho^2 & \mbox{ para } 1 < i < n \\ \Sigma^{-1}_{i,j} = -\rho & \mbox{ para } |i-j| = 1 \\ \Sigma^{-1}_{i,j} = 0 & \mbox{ para } |i-j| > 1 \end{array} \right. \]
A matriz para os dados simulados poderia ser montada da forma como mostrado a seguir onde exibimos as cinco primeiras linhas e colunas.
iS <- diag(1+0.7^2, n)
diag(iS)[1] <- diag(iS)[n] <- 1
iS[abs(row(iS)-col(iS))==1] <- -0.7
iS[1:5, 1:5]## [,1] [,2] [,3] [,4] [,5]
## [1,] 1.0 -0.70 0.00 0.00 0.00
## [2,] -0.7 1.49 -0.70 0.00 0.00
## [3,] 0.0 -0.70 1.49 -0.70 0.00
## [4,] 0.0 0.00 -0.70 1.49 -0.70
## [5,] 0.0 0.00 0.00 -0.70 1.49Desta forma o código pode ser escrito de forma ainda mais eficiente evitando inversão de matriz (ou a solução de sistemas lineares) no cálculo da forma quadrática. Além disto, o determinante de \(\Sigma\) possui expressão conhecida \({\rm det}(\Sigma) = 1/(1-\rho^2)\). Com estes resultados o cálculo da verossimilhança pode ser substancialmente acelerado em comparação com os códigos anteriores, conforme mostra o código a seguir.
## [1] -139## [1] -139## [1] -139## [1] -139## [1] -139## [1] -139## [1] -139system.time(replicate(100, {iSchol <- chol(iS)
(-n/2) * log(2*pi) + sum(log(diag(iSchol))) -
0.5*drop(crossprod(iSchol %*% y))}))## user system elapsed
## 0.034 0.000 0.035system.time(replicate(100, 0.5*(-n*log(2*pi) + log(1-0.7^2) -
mahalanobis(y, center=0, cov=iS, inverted=TRUE))))## user system elapsed
## 0.01 0.00 0.01system.time(replicate(100, 0.5*(-n*log(2*pi) + log(1-0.7^2) -
drop(crossprod(y, iS %*% y)))))## user system elapsed
## 0.002 0.000 0.002Finalmente vamos comparar com o tempo para o cálculo utilizando a forma fatorada da verossimilhança, ou seja, com o produto de distribuições univariadas.
system.time(replicate(100, llAR1(0.7, dados=y)))## user system elapsed
## 0.001 0.000 0.001E ainda há outras melhorias possíveis! A matriz inversa \(\Sigma^{-1}\) é esparsa (muitos elementos iguais a zero) e algorítmos e funções específicas como os do pacote Matrix podem ser utilizados não só para eficiência mas também para reduzir o uso de memória para armazenar tais matrizes. Deixamos tal implementação como sugestão ao leitor.
No código 4.4 implementamos a função de verossimilhança que é depois maximizada para obter a estimativa do parâmetro \(\rho\).
llAR1mv <- function(par, sigma = 1, dados){
n <- length(dados)
iS <- diag(1+par^2, n)
diag(iS)[1] <- diag(iS)[n] <- 1
iS[abs(row(iS)-col(iS))==1] <- -par
return(0.5*(-n*log(2*pi) - 2*n*log(sigma) + log(1-par^2) -
drop(crossprod(dados, iS %*% dados))/sigma^2))
}unlist(optimize(llAR1mv, c(0,1), dados=y, maximum=TRUE))## maximum objective
## 0.72 -138.93Vamos agora não mais fixar o valor para a variância \(\sigma^2\) e considerá-la um parâmetro também a ser estimado. Neste caso os elementos da matrix de covariância em 4.4 são \(\Sigma_{ij} = \rho^{|i-j|}(\sigma^2/(1-\rho^2))\). A função de log-verossimilhança \(l(\underline{\theta}) = l(\sigma, \rho)\) fica como a seguir. A implementação supõe que o primeiro argumento da função é um vetor de comprimento dois com os valores para \(\sigma\) e \(\rho\) , nesta ordem.
llAR1mv2 <- function(par, dados, repar=FALSE){
## par: vetor com valores de (sigma, rho), nesta ordem
n <- length(dados)
if(repar){
sigma <- exp(par[1])
rho <- (exp(2*par[2])-1)/(exp(2*par[2])+1)
}
else{ sigma <- par[1]; rho <- par[2]}
iS <- diag(1+rho^2, n)
diag(iS)[1] <- diag(iS)[n] <- 1
iS[abs(row(iS)-col(iS))==1] <- -rho
return(0.5*(-n*log(2*pi) - 2*n*log(sigma) + log(1-rho^2) -
drop(crossprod(dados, iS %*% dados))/sigma^2))
}Nesta parametrização do modelo AR1 temos que o espaço paramétrico é restrito \(\sigma > 0\) e \(|\rho| < 1\). Uma possível reparametrização para qual o espaço paramétrico é o \(\Re^2\) é adotar \(\tau = \log(\sigma)\) e a transformação de Fisher \(\varphi = \frac{1}{2} \log\left(\frac{1+\rho}{1-\rho}\right)\). Esta opção é implementada pelo argumento repar na função de verossimilhança definida em 4.5. Desta forma as três chamadas a seguir produzem o mesmo valor.
O código para obter as estimativas dos parâmetros por maximização numérica para os casos sem e com reparametrização é dado a seguir. No primeiro caso é necessário utilizar o método L-BFGS-B para poder delimitar o espaço paramétrico com os argumentos lower e upper. No segundo caso isto não é necessário uma vez que o espaço paramétrico para o modelo reparametrizado é irrestrito. Pelo princípio da invariância tem-se que os valores maximizados das verossimilhanças são iguais. Eventuais diferenças, se houverem devem ser pequenas e devidas a erros numéricos. Mostramos ainda como os valores das estimativas no segundo caso, quando transformados de volta, produzem os mesmos valores.
opar <- optim(c(1, 0.7), fn=llAR1mv2, dados=y, method="L-BFGS-B",
lower=c(0, -1), upper = c(Inf, 1),
control=list(fnscale=-1), hessian=TRUE)
unlist(opar[1:2]) ## par1 par2 value
## 0.966 0.721 -138.818rpar <- optim(c(log(1), 0.5* log((1+0.7)/(1-0.7))), fn=llAR1mv2,
dados=y, repar=TRUE, control=list(fnscale=-1), hessian=TRUE)
unlist(rpar[1:2])## par1 par2 value
## -0.0345 0.9089 -138.8181c(exp(rpar[[1]][1]), (exp(2*rpar[[1]][2])-1)/(exp(2*rpar[[1]][2])+1))## [1] 0.966 0.721A Figura 4.3 mostra as superfícies de verossimilhança para ambas parametrizações. Neste caso, a parametrização original produziu contornos mais próximos de um comportamento quadrático. Outro fato relevante revelado na figura é a quase ortogonalidade entre os parâmetros que pode ser observada em ambos os casos. Isto pode ser verificado numericamente na matriz de covariância dos estimadores obtida pela inversa da matriz de informação observada. Temos aqui que os elementos fora da diagonal possuem valores pequenos em comparação com os da diagonal, ou seja a matriz é proxima de uma matriz diagonal.

Figura 4.3: Superfícies de deviance para o modelo AR1 para parâmetros originais (esquerda) e reparametrizado (direita).
-solve(opar$hessian)## [,1] [,2]
## [1,] 4.67e-03 -6.62e-05
## [2,] -6.62e-05 4.57e-03-solve(rpar$hessian)## [,1] [,2]
## [1,] 0.005000 -0.000142
## [2,] -0.000142 0.019791Vamos focar agora na inferência sobre o parâmetro \(\rho\) neste modelo de dois parâmetros, ou seja, o parâmetro \(\sigma^2\) é considerado nuisance. No modelo definido em (4.3) a matriz de covariâncias pode ser reescrita como \(\Sigma = \sigma^2 R_{\rho}\) destacando que a matriz de correlação \(R_{\rho}\) tem seus termos dependendo apenas do parâmetro \(\rho\). A função de verrosimilhança (4.3) fica equivalente a \[\begin{equation} \mathrm{l}(\boldsymbol{\theta}) = \mathrm{l}(\sigma, \rho) = -\frac{n}{2}\log(2\pi) - \frac{n}{2}\log(\sigma^2) - \frac{1}{2}|R_{\rho}| - \exp\{\frac{1}{2\sigma^2}y^{\prime} R_{\rho}^{-1}y\} . \tag{4.5} \end{equation}\]
Tomando-se a derivada em relação à \(\sigma^2\) e igualando à zero obtém-se o estimador deste parâmetro em relação à \(\rho\), \[ \hat{\sigma}_{\rho}^2 = \frac{y^{\prime} R_{\rho}^{-1}y}{n} .\]
A verossimilhança concentrada ou perfilhada de \(\rho\) é então obtida substituindo-se \(\sigma^2\) por \(\hat{\sigma}_{\rho}^2\) em (4.5) e temos então: \[\mathrm{pl}(\rho) = -\frac{n}{2}\left(\log(2\pi) + \log(\sigma^2) + 1\right) - \frac{1}{2} \log(|R_{\rho}|) . \] Esta função é implementada em 4.6 e retorna dois valores: o da verossilhança \(\mathrm{l}(\rho, \sigma^2_{\rho})\) e de \(\sigma^2_{\rho}\), a estimativa de \(\sigma^2_{\rho}\) ao valor de \(\rho\).
A implementação da função de verossimilhança perfilhada é simples. Tomamos a verossilhança que tem apenas \(\rho\) como parâmetro e adicionamos a opção para que se \(\sigma\) não for fornecido seja calculado para o valor corrente de \(\rho\). Se o valor de \(\sigma\) for fornecido é tomado como constante e a verossimilhança condicional à este valor é calculada.
llAR1.rho <- function(rho, sigma, dados){
n <- length(dados)
iS <- diag(1+rho^2, n)
diag(iS)[1] <- diag(iS)[n] <- 1
iS[abs(row(iS)-col(iS))==1] <- -rho
if(missing(sigma))
sigma2 <- drop(crossprod(dados, iS %*% dados)/n)
else sigma2 <- sigma^2
return(0.5*(-n*log(2*pi) - n*log(sigma2) + log(1-rho^2) -
drop(crossprod(dados, iS %*% dados))/sigma2))
}O gráfico da deviance perfilhada é visualizado à direita na Figura 4.4. Também é traçada a verossimilhança condicional na qual o valor de \(\sigma^2\) é fixado em sua estimativa de máxima verossimilhança \[\hat{\sigma}^2 = \hat{\sigma}_{\hat{\rho}}^2 = \frac{y^{\prime} \hat{R}_{\hat{\rho}}^{-1}y}{n} .\]
As funções diferem considerando uma maior região do espaço paramétrico conforme mostrado no gráfico do centro. Entretanto, na região do espaço paramétrico relevante para inferências no entorno do ponto de máximo as funções são quase indistinguíveis. Isto é mais um reflexo da quase ortogonalidade entre os parâmetros ao redor do máximo da função. No gráfico da deviance mostrada à esquerda e linhas indicam os cortes para obtenção das perfilhadas e condicionais.
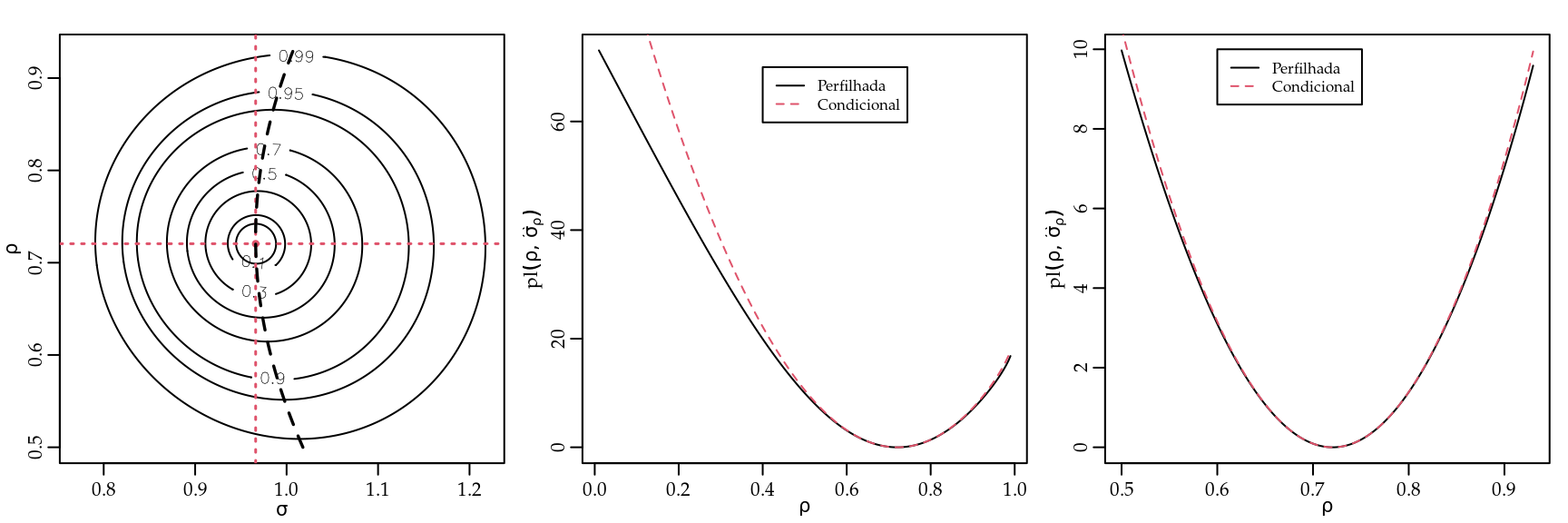
Figura 4.4: Superfície de deviance (esquerda) com indicações dos cortes para obtenção das perfilhadas e condicionais. Deviances perfilhadas e condicionais para o parâmetro $ ho$ do modelo AR1.
Para finalizar consideramos o modelo AR1 mais geral, que inclui um termo para descrever a média do processo. Uma forma de escrever tal modelo é: \[\begin{align} y_{y+1} &= \alpha + \rho y_t + e_{t+1} \\ e_{t+1} & \sim {\rm N}(0, \sigma^2) \tag{4.6} \end{align}\] A média do processo é dada por: \[ {\rm E}[y_t] = \mu = \frac{\alpha}{1-\rho}, \] e o modelo acima pode ser então reescrito na forma: \[\begin{equation} y_{y+1} = (1-\rho) + \rho y_t + e_{t+1}. \tag{4.7} \end{equation}\] Para a expressão da verossimilhança, simplesmente acrescenta-se o termo de média a (4.8) que fica: \[\begin{equation} l(\underline{\theta}) = l(\sigma, \rho) = -\frac{n}{2}\log(2\pi) - \frac{1}{2}\log(|\Sigma|) - \exp\{\frac{1}{2}(y-\mu)^{\prime} \Sigma^{-1})y-\mu)\}. \tag{4.8} \end{equation}\]
O código retornando o negativo da função de verossimilhança é implementado em 4.7 e a seguir são mostradas as estimativas para os dados aqui considerados.
llAR1mv3 <- function(par, dados){
## par: vetor com valores de (mu, sigma, rho), nesta ordem
n <- length(dados)
mu <- par[1]; sigma <- par[2]; rho <- par[3]
iS <- diag(1+rho^2, n)
diag(iS)[1] <- diag(iS)[n] <- 1
iS[abs(row(iS)-col(iS))==1] <- -rho
ymu <- dados - (1-rho)*mu
return(-0.5*(-n*log(2*pi) - 2*n*log(sigma) + log(1-rho^2) -
drop(crossprod(ymu, iS %*% ymu))/sigma^2))
}llAR1mv3(c(0,1,0.5), dados=y)## [1] 144par3 <- optim(c(0,1,0.5), llAR1mv3, hessian=TRUE, dados=y)
unlist(par3[1:2])## par1 par2 par3 value
## 1.712 0.950 0.663 137.052round(solve(par3$hessian), dig=4)## [,1] [,2] [,3]
## [1,] 0.8074 -0.0003 0.0266
## [2,] -0.0003 0.0045 -0.0001
## [3,] 0.0266 -0.0001 0.0054Existem pacotes e funções específicas para ajustar modelos de séries temporais no R,
descritos na Time Series Task View[http://cran.r-project.org/web/views/TimeSeries.html]
As funções ar() e arima() estão entre as disponíveis e produzem resultados como mostrado a seguir, que diferem dos anteriores pois incluem a média na estimação o modelo com três parâmetros \((\mu, \sigma, \rho)\).
(fit.ar <- ar(y, order.max=1, method="mle"))##
## Call:
## ar(x = y, order.max = 1, method = "mle")
##
## Coefficients:
## 1
## 0.663
##
## Order selected 1 sigma^2 estimated as 0.902with(fit.ar, x.mean)## [1] 0.576(fit.arima <- arima(y, order=c(1,0,0), method="ML"))##
## Call:
## arima(x = y, order = c(1, 0, 0), method = "ML")
##
## Coefficients:
## ar1 intercept
## 0.663 0.576
## s.e. 0.073 0.277
##
## sigma^2 estimated as 0.902: log likelihood = -137, aic = 280Note que enquanto nosso código retorna as estimativas de \((\mu, \sigma, \rho)\) na parametrização definida em (4.7) as funções ar() e arima() retornam estimativas de \((\alpha, \sigma^2, \rho)\) definida em (4.6).
\[ \begin{align*} 0.576 &= \hat{\alpha} = (1-\hat{\rho}) \hat{\mu} = (1 - 0.663) \cdot 1.712 = 0.576\\ 0.902 &= \hat{\sigma}^2 = 0.95^2 = 0.902 \end{align*} \]
Aproveitamos esta última função para ilustrar e funcionalidade do pacote bbmle e da função genérica de ajuste de modelos mle2(). A função recebe o negativo da log-verossimilhança do modelo desejado, tal como em 4.7 neste exemplo.
Internamente a função optim() é utilizada por default na otimização e outras podem ser selecionadas. Entretando a função envoltório mle2() prepara os resultados de forma que várias explorações do ajuste tais como intervalos de confiança e verossimilhnaças perfilhadas podem ser facilmente obtidas, sem a necessidade de programações adicionais.
llAR1.bb <- function(mu, sigma, rho, dados){
n <- length(dados)
iS <- diag(1+rho^2, n)
diag(iS)[1] <- diag(iS)[n] <- 1
iS[abs(row(iS)-col(iS))==1] <- -rho
ymu <- dados - (1-rho)*mu
return(-0.5*(-n*log(2*pi) - 2*n*log(sigma) + log(1-rho^2) -
drop(crossprod(ymu, iS %*% ymu))/sigma^2))
}O ajuste produz os mesmos resultados obtidos anteriormente por outros métodos.
require(bbmle)
ar1bb <- mle2(llAR1.bb, start=list(mu=0, sigma=1, rho=0.5),
data=list(dados=y))
coef(ar1bb)## mu sigma rho
## 1.712 0.950 0.663logLik(ar1bb)## 'log Lik.' -137 (df=3)4.2 Tratando tudo numericamente
Vimos nos exemplos anteriores que métodos numéricos são essenciais em inferência baseada em verossimilhança. Mesmo em exemplos simples com apenas dois parâmetros soluções analíticas não podem ser obtidas. Vimos também que o algoritmo de Newton-Raphson é muito poderoso para resolver sistemas do tipo \(f(x)=0\), porém ele necessita do vetor escore e da matriz de derivadas segundas (Hessiana), o que nem sempre pode ser fácil de ser obtido e mesmo em exemplos simples pode demandar trabalho computacional e/ou analítico considerável.
Além disso, vimos que a implementação de intervalos baseados em perfil de
verossimilhança é um tanto quanto tediosa, mesmo os intervalos de Wald que são
simples exigem de um tempo razoável de programação que precisa ser muito
cuidadosa para evitar problemas e exceções numéricas. Nesta seção nos vamos
abordar os mesmos três problemas a dois parâmetros já apresentados porém
tratando eles de forma inteiramente numérica, o que pode ser útil para
investigar, ainda que preliminarmente, o comportamento de modelos existentes ou
em desenvolvimento. Para isto, vamos usar a função optim() que
implementa quatro poderosos algoritmos de otimização numérica, são eles
Nelder-Mead, Gradiente Conjugado, Simulating Annealing e BFGS.
Porém, só esta função não resolve o problema da construção dos intervalos de
confiança e testes de hipóteses. Para isto, vamos introduzir o pacote
bbmle que traz uma verdadeira “caixa de ferramentas” para inferência
baseada em verossimilhança. Ilustramos o uso mostrando que com pouca
programação conseguiremos estimar os parâmetros, construir intervalos de
confiança assintóticos e perfilhados, obter testes de hipóteses, além de obter
os resultados apresentados como no padrão de funções centrais do R como a
lm() e glm().
Veremos também como os resultados analíticos já obtidos, principalmente o vetor
escore, podem ser usados para acelerar e melhorar a performance dos otimizadores
numéricos. Relembre que no Exemplo 3.1, tratamos o modelo
gaussiano com média \(\mu\) e variância \(\sigma^2\). Podemos escrever o
negativo da log-verossimilhança deste modelo em R da seguinte forma:
ll.gauss <- function(par, dados){
return(-sum(dnorm(dados, par[1], sd=par[2], log=TRUE)))}Note que retornamos o negativo da log-verossimilhança simplesmente porque, por
padrão, a função optim() minimiza a função objetivo. Informamos um vetor
em que cada posição corresponde a cada parâmetro a ser estimado. Para proceder
o processo de estimação precisamos de uma amostra, vamos simular uma amostra de
tamanho \(n=100\) do modelo gaussiano com \(\mu=10\) e \(\sigma=2\) apenas para
ilustrar o procedimento estimação via a função optim(). Na maioria dos
algoritmos de otimização numérica será necessário o uso de valores iniciais,
para isto é comum utilizar alguma estimativa grosseira ou mesmo fazer várias
tentativas e avaliar a sensibilidade do algoritmo as condições iniciais.
Um cuidado que se deve ter quando se usa este tipo de algoritmo numérico é o
espaço de busca, que no caso de inferência estatística corresponde ao espaço
paramétrico. Para o parâmetro \(\mu\) a busca deve ser em toda a reta real, porém
para \(\sigma\) apenas nos reais positivos. A maioria dos algoritmos da
optim() não leva isso em consideração, fazendo com que se tente avaliar a
função de verossimilhança em pontos não válidos. Este problema pode gerar desde
simples mensagens de warnings até a falha total do algoritmo. O único
algoritmo dentro da optim() que permite busca em espaços determinados é o
L-BFGS-B é o que vamos usar neste exemplo. Reparametrizações são muito
úteis neste ponto para permitir o uso de outros algorítmos que busquem solução
no espaço paramétrico irrestrito. No exemplo de estimação da normal \(\sigma \in \Re^*_{+}\)
uma reparametrização conveniente seria \(\tau = \log(\sigma) \in \Re\).
Recomendamos que o leitor leia a documentação da função e experimente os outros
algoritmos.
set.seed(123)
dados <- rnorm(100, m=10, s=2)
unlist(est.gauss <- optim(par=c(5, 1), fn = ll.gauss, dados=dados,
method="L-BFGS-B", lower=c(-Inf, 0.1),
upper=c(Inf,Inf), hessian=TRUE)[1:2])## par1 par2 value
## 10.18 1.82 201.58A saída da optim() retorna uma lista.
O primeiro elemento é o valor que maximiza o negativo da log-verossimilhança.
Em seguida o valor maximizado que a função toma neste ponto.
Tal valor é muito importante para a construção de testes de hipóteses e comparações de modelos.
Na sequência diversas informações sobre o procedimento e, por fim, a matriz hessiana é obtida numericamente,
a qual é importante para a construção dos intervalos de confiança assintóticos.
Deste ponto, ainda é preciso uma quantidade razoável de programação para obtenção de intervalos baseados na verossimilhança perfilhada.
Uma forma mais rápida de obter praticamente tudo que se deseja do processo de inferência é usar
funções disponíveis em pacotes tais como o bbmle, que implementam os procedimentos de forma genérica
e facilitam todo o procedimento.
Para usar as funcionalidades do pacote bbmle precisamos escrever a função de log-verossimilhança de forma ligeiramente diferente.
O código abaixo apresenta as funções de log-verossimilhança para os casos Gaussianos, Gama e Binomial Negativo discutidos anteriormente
neste Capítulo.
ll.gauss <- function(mu, sigma, dados){
return(-sum(dnorm(dados, mu, sigma, log=TRUE)))
}
ll.gamma <- function(a,s, dados){
return(-sum(dgamma(dados,shape=a,scale=s, log=TRUE)))}
ll.negbin <- function(phi, p, dados){
return(-sum(dnbinom(dados,size=phi, p=p, log=TRUE)))}A estimação via o pacote bbmle é feita através da função mle2(),
que é apenas uma “casca” para a optim() mas facilita a entrada de dados e
formata os resultados de forma conveniente.
Para o modelo gaussiano teríamos o código a seguir.
require(bbmle)
est.gauss <- mle2(ll.gauss, start=list(mu=8, sigma=3),
data=list(dados=dados), method="L-BFGS-B",
lower=list(mu=-Inf, sigma=0.1),
upper=list(mu=Inf, sigma=Inf))Neste formato os resultados podem ser explorados desde um simples resumo do modelo ajustado via função summary(),
summary(est.gauss)## Maximum likelihood estimation
##
## Call:
## mle2(minuslogl = ll.gauss, start = list(mu = 8, sigma = 3), method = "L-BFGS-B",
## data = list(dados = dados), lower = list(mu = -Inf, sigma = 0.1),
## upper = list(mu = Inf, sigma = Inf))
##
## Coefficients:
## Estimate Std. Error z value Pr(z)
## mu 10.181 0.182 56.0 <2e-16 ***
## sigma 1.816 0.128 14.1 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## -2 log L: 403construção de intervalos de confiança assintóticos,
confint(est.gauss,method="quad")## 2.5 % 97.5 %
## mu 9.82 10.54
## sigma 1.56 2.07ou construção de intervalos de confiança perfilhados.
confint(est.gauss)## 2.5 % 97.5 %
## mu 9.82 10.5
## sigma 1.59 2.1O código a seguir mostra o procedimento para o caso Gama.
Note a definição dos intervalos de busca para o algoritmo L-BFGS-B.
set.seed(123)
dados.gama <- rgamma(100, shape=10, scale=1)
est.gamma <- mle2(ll.gamma, start=list(a=2,s=10),
data=list(dados=dados.gama), method="L-BFGS-B",
lower=list(a=1e-32,s=1e-32), upper=list(a=Inf,s=Inf))
summary(est.gamma)## Maximum likelihood estimation
##
## Call:
## mle2(minuslogl = ll.gamma, start = list(a = 2, s = 10), method = "L-BFGS-B",
## data = list(dados = dados.gama), lower = list(a = 1e-32,
## s = 1e-32), upper = list(a = Inf, s = Inf))
##
## Coefficients:
## Estimate Std. Error z value Pr(z)
## a 13.536 1.891 7.16 8.2e-13 ***
## s 0.723 0.103 7.03 2.1e-12 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## -2 log L: 474confint(est.gamma)## 2.5 % 97.5 %
## a 10.165 17.594
## s 0.554 0.969confint(est.gamma,method="quad")## 2.5 % 97.5 %
## a 9.830 17.243
## s 0.521 0.925De forma análoga pode-se obter resultados para o modelo Binomial Negativo.
set.seed(123)
dados.nbin <- rnbinom(1000, size=10, p=0.8)
est.nbin <- mle2(ll.negbin,start=list(phi=2, p=0.5),
data=list(dados=dados.nbin), method="L-BFGS-B",
lower=list(phi=1e-32, p= 1e-32),
upper=list(phi=Inf,p=0.99999))
summary(est.nbin)## Maximum likelihood estimation
##
## Call:
## mle2(minuslogl = ll.negbin, start = list(phi = 2, p = 0.5), method = "L-BFGS-B",
## data = list(dados = dados.nbin), lower = list(phi = 1e-32,
## p = 1e-32), upper = list(phi = Inf, p = 0.99999))
##
## Coefficients:
## Estimate Std. Error z value Pr(z)
## phi 8.6344 1.7362 4.97 6.6e-07 ***
## p 0.7725 0.0356 21.72 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## -2 log L: 3854confint(est.nbin,method="quad") # assintotico## 2.5 % 97.5 %
## phi 5.232 12.037
## p 0.703 0.842confint(est.nbin) # perfilhada## 2.5 % 97.5 %
## phi 6.083 13.705
## p 0.704 0.844O esforço de programação quando tratamos tudo numericamente, sem utilizar resultados analíticos parciais é menor
e adequado em explorações preliminares de modelos.
Entretanto, note-se que isto torna a inferência computacionalmente mais cara e potencialmente mais instável.
O uso das funções do pacote bbmle facilita muito o trabalho de inferência,
pois já implementa métodos genéricos, além de
formatar adequadamente a saída na forma de outras funções padrão do R.
Implementações para uso intensivo podem, em algumas situações, ser porteriormente ajustadas para
um melhor desempenho, se necessário.
Finalmente, é importante dizer que as implementações feitas neste Capítulo visam primariamente ilustrar conceitos de inferência e o uso da linguagem. Algorítmos e funções mais gerais e eficientes podem ser escritos ou, pode-se ainda em muitos casos, utilizar funções já prontas dsiponibilizadas em pacotes específicos. Por exemplo, para a classe de modelos na família exponencial, que engloba todas as distribuições usadas aqui, é possível escrever expressões gerais, válidas para todas estas distribuições. Neste caso, as expressões no Método de Newton-Raphson podem ser escritas na forma de um procedimento iterativo de minímos quadrados que são reponderados a cada iteração (IRWLS - iteractive reweighted least squares). Por outro lado os códigos ilustram implementações que podem seguir de guia para programação de modelos de interesse que não estejam já implementados.