Chapter 2 Definições e propriedades
Neste Capítulo apresentamos os três objetivos fundamentais da inferência estatística, estimação pontual, intervalar e teste de hipóteses através da função de verossimilhança.
Definição 2.1 Função de verossimilhança - Seja \(\mathbf{y}\) um vetor \(n \times 1\) representando uma realização de um vetor aleatório \(\mathbf{Y}\) com função de probabilidade ou densidade probabilidade \(\mathrm{f}(\mathbf{Y},\boldsymbol{\theta})\), onde \(\boldsymbol{\theta}\) denota um vetor \(p \times 1\) de parâmetros, com \(\boldsymbol{\theta} \in \Theta\), sendo \(\Theta\) o respectivo espaço paramétrico. A função de verossimilhança ou simplesmente verossimilhança para \(\boldsymbol{\theta}\) dado os valores observados \(\mathbf{y}\) é a função \(\mathrm{L}(\boldsymbol{\theta}| \mathbf{y}) \equiv \mathrm{f}(\mathbf{Y},\boldsymbol{\theta})\).
A função de verossimilhança é dada pela expressão da distribuição conjunta de todas as variáveis aleatórias envolvidas no modelo, porém vista como função dos parâmetros, uma vez que tendo os dados sido observados, são quantidades fixas. Para cada particular valor do parâmetro que pode ser escalar ou vetor, a verossimilhança é uma medida de compatibilidade, plausibilidade ou similaridade do modelo com a amostra observada medida pela probabilidade ou densidade conjunta dos valores observados. Fracamente falando, pode-se dizer que a verossimilhança nos fornece a probabilidade de observar o que foi realmente observado, dado o modelo assumido para os dados.
A expressão da verossimilhança \(\mathrm{L}(\boldsymbol{\theta}| \mathbf{y})\)
pode ser mais cuidadosamente definida considerando a natureza das variáveis aleatórias.
Para modelos discretos não há ambiguidade e o valor da função de verossimilhança é a probabilidade de ocorrer o dado observado, ou seja
\[
\mathrm{L}(\boldsymbol{\theta}|\mathbf{y}) \equiv \mathrm{P}_{\boldsymbol{\theta}}(\mathbf{Y}=\mathbf{y}). \]
No caso de modelos contínuos a probabilidade de um particular conjunto de
valores ser observado é nula. Entretanto, na prática medidas contínuas são tomadas com algum grau de precisão em um intervalo, digamos,
\(y_{iI} \leq y_i \leq y_{iS}\) e a verossimilhança para um conjunto de observações é:
\[\begin{equation}
\mathrm{L}(\boldsymbol{\theta}|\mathbf{y}) = \mathrm{P}_{\boldsymbol{\theta}}(y_{1I} \leq y_1 \leq y_{1S}, y_{2I} \leq y_2 \leq y_{2S},
\ldots, y_{nI} \leq y_n \leq y_{nS}).
\tag{2.1}
\end{equation}\]
Esta definição é geral e requer a especificação da distribuição conjunta
de \(\mathrm{Y}\). Fazendo a suposição de observações independentes tem-se que:
\[\begin{equation}\label{eq:veroind}
\mathrm{L}(\boldsymbol{\theta}|\mathbf{y}) = \mathrm{P}_{\boldsymbol{\theta} }(y_{1I} \leq y_1 \leq y_{1S}) \cdot \mathrm{P}_{\boldsymbol{\theta}}(y_{2I} \leq y_2 \leq y_{2S}), \ldots ,
\mathrm{P}_{\boldsymbol{\theta}}(y_{nI} \leq y_n \leq y_{nS}).
\end{equation}\]
Até este ponto a definição pode ser utilizada tanto para dados considerados
pontuais quanto para dados intervalares, como no caso de dados censurados.
Vamos supor agora uma situação mais simples e comum na qual todos os dados
são medidos a um grau de precisão comum.
Neste caso, cada dado é medido em um intervalo
\((y_i - \delta/2 \leq Y_i \leq y_i + \delta/2)\)
e a verossimilhança é dada por:
\[\begin{align*}
\mathrm{L}(\boldsymbol{\theta}|\mathbf{y}) &= \prod_{i=1}^n \mathrm{P}_{\boldsymbol{\theta} }(y_i - \delta/2 \leq Y_i \leq y_i + \delta/2) \\
&= \prod_{i=1}^n \int_{y_i - \delta/2}^{y_i + \delta/2} \mathrm{f}(y_i , \boldsymbol{\theta}) \mathrm{d}y_i.
\end{align*}\]
Se o grau de precisão é alto, ou seja \(\delta\) é pequeno em relação a variabilidade dos dados a expressão se reduz a
\[
\mathrm{L}(\boldsymbol{\theta}|\mathbf{y}) \approx \left(\prod_{i=1}^n \mathrm{f}(y_i, \boldsymbol{\theta}) \right) \delta^n ,
\tag{2.2}
\]
e se \(\delta\) não depende dos valores dos parâmetros temos a verossimilhança
como produto das densidades individuais,
\[\begin{equation}\label{eq:veroiid}
\mathrm{L}(\boldsymbol{\theta}|\mathbf{y}) \approx \prod_{i=1}^n \mathrm{f}(y_i, \boldsymbol{\theta}) ,
\end{equation}\]
e de forma mais geral para observações não independentes
com a densidade multivariada:
\[\begin{equation}\label{eq:veromv}
\mathrm{L}(\boldsymbol{\theta}|\mathbf{y}) \approx \mathrm{f}(\mathbf{y}, \boldsymbol{\theta}) .
\end{equation}\]
No caso onde os elementos de \(\mathbf{y}\) são independentes a verossimilhança é simplesmente um produto das distribuições de cada variável aleatória \(Y_i\) individualmente, ou seja, \(\mathrm{L}(\boldsymbol{\theta}| \mathbf{y}) = \prod_{i=1}^n \mathrm{f}(y_i, \boldsymbol{\theta})\). Neste caso, o procedimento de inferência pode ser bastante facilitado tanto analítica como computacionalmente. Porém, cabe ressaltar que isso não é uma exigência, e situações onde as amostras não são independentes são tratadas da mesma forma, escrevendo a verossimilhança de uma forma adequada, considerando a distribuição conjunta do vetor \(\mathbf{Y}\).
Esta parte do texto concentra-se exclusivamente no uso da função de verossimilhança como base para explicar os aspectos envolvidos na inferência estatística, seja na obtenção de estimativas pontuais, intervalares ou testes de hipóteses. Começamos revisando conceitos de estimação e suas relações com a função de verossimilhança.
2.1 Estimação pontual
Seja \(Y_1, Y_2, \ldots, Y_n\) variáveis aleatórias com forma conhecida da função probabilidade no caso de variáveis aleatórias discretas ou da função densidade de probabilidade para variáveis aleatórias contínuas, em ambos os casos denotadas por \(\mathrm{f}(\mathbf{Y}, \boldsymbol{\theta})\). O vetor \(\boldsymbol{\theta}\) denota os parâmetros desconhecidos, sendo que um único elemento de \(\boldsymbol{\theta}\) será denotado por \(\theta\), o qual queremos estimar através de uma amostra \(y_1, y_2, \ldots, y_n\), de realizações das variáveis aleatórias \(Y_1, Y_2, \ldots, Y_n\). Denota-se de forma simplificada, \(Y_i \sim \mathrm{f}(\boldsymbol{\theta})\) com \(i = 1, \ldots, n\). Esta notação deve ser lida da seguinte forma: a variável aleatória \(Y_i\) segue uma distribuição \(\mathrm{f(\cdot)}\) que por sua vez é indexada, descrita ou governada por um vetor de parâmetros \(\boldsymbol{\theta}\). A seguir apresentamos algumas definições importantes para o decorrer do texto.
Definição 2.2 Estatística - Uma estatística é uma variável aleatória \(\mathrm{T} = \mathrm{t}(\mathbf{Y})\), onde a função \(\mathrm{t}(\cdot)\) não depende de \(\boldsymbol{\theta}\).
Definição 2.3 Estimador - Uma estatística \(\mathrm{T}\) é um estimador para \(\theta\) se o valor realizado \(\mathrm{t} = \mathrm{t}(\boldsymbol{y})\) é usado como uma estimativa para o valor de \(\theta\).
Definição 2.4 Distribuição amostral - A distribuição de probabilidade de \(\mathrm{T}\) é chamada de distribuição amostral do estimador \(\mathrm{t}(\mathbf{Y})\).
Definição 2.5 Viés - O viés de um estimador \(\mathrm{T}\) é a quantidade \[\mathrm{B}(\mathrm{T}) = \mathrm{E}(\mathrm{T} - \theta).\] O estimador \(\mathrm{T}\) é dito não viciado para \(\theta\) se \(\mathrm{B}(\mathrm{T}) = 0\), tal que \(\mathrm{E}(\mathrm{T}) = \theta\). O estimador \(\mathrm{T}\) é assintoticamente não viciado para \(\theta\) se \(\mathrm{E}(\mathrm{T}) \to \theta\) quando \(n \to \infty\).
Definição 2.6 Eficiência relativa - A eficiência relativa entre dois estimadores \(\mathrm{T_1}\) e \(\mathrm{T_2}\) é a razão \(\mathrm{er} = \frac{\mathrm{V}(\mathrm{T_1})}{\mathrm{V}(\mathrm{T_2})}\) em que \(\mathrm{V}(\cdot)\) denota a variância do respectivo estimador.
Definição 2.7 Erro quadrático médio - O erro quadrático médio de um estimador \(\mathrm{T}\) é a quantidade \[ \mathrm{EQM}(\mathrm{T}) = \mathrm{E}( ( \mathrm{T} - \theta)^2 ) = \mathrm{V}(\mathrm{T}) + \mathrm{B}(\mathrm{T})^2 . \]
Definição 2.8 Consistência - Um estimador \(\mathrm{T}\) é médio quadrático consistente para \(\theta\) se o \(\mathrm{EQM}(\mathrm{T}) \to 0\) quando \(n \to \infty\). O estimador \(\mathrm{T}\) é consistente em probabilidade se \(\forall \epsilon > 0\), \(\mathrm{P}( | \mathrm{T} - \theta | > \epsilon) \to 0\), quando \(n \to \infty\).
Estas definições introduzem conceitos e propriedades básicas para uma estatística ser um estimador adequado para um determinado parâmetro. Fracamente falando, o desejo é obter um estimador que seja assintóticamente não-viciado, ou seja, conforme o tamanho da amostra aumenta ele se aproxima cada vez mais do verdadeiro valor do parâmetro. Além disso, é interessante que ele seja eficiente, ou seja, apresente a menor variância possível entre todos os estimadores de \(\theta\). Esta definição de eficiência, introduz o conceito de variância minima. Sendo assim, para saber se um estimador é eficiente é necessário conhecer um limite inferior para a variância de um estimador, uma vez que tal quantidade exista e seja passível de calcular, ao propor um estimador para \(\theta\), basta calcular a sua variância e comparar com a menor possível, se ele atingir este limite será eficiente. Além disso, tomando sua esperança pode-se concluir sobre o seu viés dependendo da situação em termos assintóticos. O Teorema (limite inferior de Cramér-Rao) 2.1, ajuda a responder sobre a eficiência de um estimador qualquer. Mas antes precisamos de mais algumas definições.
Como dito, a verossimilhança é uma medida de compatibilidade da amostra observada com um particular vetor de parâmetros, desta forma é natural definir como estimador para o vetor de parâmetros \(\boldsymbol{\theta}\), aquele particular vetor digamos, \(\hat{\boldsymbol{\theta}}\), que tenha a maior compatibilidade com a amostra, ou em outras palavras o vetor que maximiza a função de verossimilhança ou compatibilidade. O particular valor assumido pela função de verossimilhança neste caso não é importante, o que interessa para inferência são os valores relativos de \(\mathrm{L}(\boldsymbol{\theta}|\mathrm{y})\) para diferentes conjuntos de \(\boldsymbol{\theta}\).
Definição 2.9 Estimativa de máxima verossimilhança - Seja \(\mathrm{L}(\boldsymbol{\theta}|\mathbf{y})\) a função de verossimilhança. O valor \(\hat{\boldsymbol{\theta}} = \hat{\boldsymbol{\theta}}(\mathbf{y})\) é a estimativa de máxima verossimilhança para \(\boldsymbol{\theta}\) se \(\mathrm{L}(\hat{\boldsymbol{\theta}}) \ge \mathrm{L}(\boldsymbol{\theta})\), \(\forall \boldsymbol{\theta} \in \Theta\).
Definição 2.10 Estimador de máxima verossimilhança - Se \(\hat{\boldsymbol{\theta}}(\mathbf{y})\) é a estimativa de máxima verossimilhança, então \(\hat{\boldsymbol{\theta}}(\mathbf{Y})\) é o estimador de máxima verossimilhança. Em geral vamos usar a abreviação EMV para nos referirmos ao estimador de máxima verossimilhança.
Nesta etapa é preciso ter cuidado com a notação. Veja que \(\hat{\boldsymbol{\theta}}(\mathbf{y})\) é um vetor de escalares, por outro lado \(\hat{\boldsymbol{\theta}}(\mathbf{Y})\) é um vetor de variáveis aleatórias. Daqui em diante usaremos apenas \(\hat{\boldsymbol{\theta}}\), para ambos os casos sendo que o contexto indicará o real sentido de \(\hat{\boldsymbol{\theta}}\). A função de verossimilhança contêm toda a informação proveniente dos dados sobre o vetor de parâmetros \(\boldsymbol{\theta}\). Apesar disso, a \(\mathrm{L}(\boldsymbol{\theta}|\mathbf{y})\) é computacionalmente incoveniente, uma vez que esta função apresentará valores muito próximos de zero, conforme o tamanho da amostra aumenta. Por razões meramente computacionais é mais comum usar a função de log-verossimilhança.
Definição 2.11 Log-verossimilhança - Se \(\mathrm{L}(\boldsymbol{\theta}|\mathbf{y})\) é a função de verossimilhança, então \(\mathrm{l}(\boldsymbol{\theta}|\mathbf{y}) = \log \mathrm{L}(\boldsymbol{\theta}|\mathbf{y})\) é a função de log-verossimilhança.
Segue do fato da função logaritmo ser monótona crescente que maximizar \(\mathrm{L}(\boldsymbol{\theta}|\mathbf{y})\) e \(\mathrm{l}(\boldsymbol{\theta}|\mathbf{y})\) levam ao mesmo ponto de máximo. Neste ponto estamos habilitados a enunciar um dos teoremas mais fortes da inferência estatística que permitirá concluir sobre a eficiência de um estimador. Neste texto vamos enunciar o Teorema apenas para um o caso em que \(\theta\) é um escalar, porém o caso multiparâmetros segue de forma analoga.
Teorema 2.1 Limite inferior de Cramer-Rao - Se \(\mathrm{T}\) é um estimador não-viciado para \(\theta\) e \(\mathrm{l}(\theta|\mathbf{Y})\) é duas vezes diferenciável com respeito a \(\theta\), então \[ \mathrm{V}(\mathrm{T}) \ge \frac{1}{\mathrm{E}( - \mathrm{l}^{\prime \prime}(\theta| \mathbf{Y}) )} . \]
Este teorema informa o limite inferior para a variância de um estimador \(\hat{\mathrm{T}}\) qualquer. O estimador de máxima verossimilhança apresenta propriedades ótimas e uma delas é a eficiência, ou seja, assintóticamente o EMV atinge o limite inferior de Cramer-Rao. Na sequência discutimos como expressar a incerteza com relação ao vetor de parâmetros \(\boldsymbol{\theta}\) através da construção de intervalos de confiança.
2.2 Intervalos de confiança
Definição 2.12 Intervalo de confiança - Um intervalo de verossimilhança para \(\theta\) é um intervalo da forma \(\theta: \mathrm{L}(\theta|\mathbf{y}) \ge r \mathrm{L}(\hat{\theta}|\mathbf{y})\) ou equivalentemente, \(\theta: \mathrm{D}(\theta) \leq c^*\), com \(\mathrm{D}(\theta) = -2[\mathrm{l}(\theta)-\mathrm{l}(\hat{\theta})]\) e \(c^* = - 2 \log(r)\).
Esta definição é bastante geral para o caso uniparamétrico, para o caso multiparâmetros os princípios se mantêm e trocamos o intervalo de confiança por uma região de confiança, o que será abordado mais adiante. Nesta definição o valor de \(r\) precisa ser especificado entre \(0\) e \(1\), para intervalos não vazios, logo \(c^* > 0\). Quanto maior o valor de \(c^*\) mais largo será o intervalo, algumas vezes o intervalo pode ser a união de sub-intervalos disjuntos, porém este caso não é usual. Apesar do valor de \(c^*\) ser necessário para a construção dos intervalos ainda não temos elementos suficientes para especificá-lo.
Usando esta definição pode-se pensar ao menos duas formas de construção de intervalos de confiança. A primeira é considerar a quantidade \(\frac{\mathrm{L}(\theta)}{\mathrm{L}(\hat{\theta})} \ge r\) que é a verossimilhança relativa, ou seja, compara cada valor de \(\theta\) com o máximo. Nestas condições a verossimilhança relativa toma sempre valores entre \(0\) e \(1\) e o intervalo é a região do espaço paramétrico para qual os valores associados de verossimilhança sejam uma fração não menor que \(r\) do máximo valor. Por exemplo, definindo \(r = 0.8\) estamos deixando que faça parte do intervalo de confiança valores que tenham até \(80\%\) de compatibilidade com a amostra observada, da mesma forma poderíamos definir \(r = 0.20\) ou \(0.50\), dependendo de nosso critério. Royall (1997) propõe que este valor seja definido por analogias com resultados considerados aceitáveis em experimentos simples como lançamento de uma moeda. Porém, em grande parte dos problemas práticos uma interpretação probabilística baseada em idéias frequentistas é usada. Voltaremos a escolha do ponto de corte mais adiante quando apresentarmos as propriedades assintóticas do EMV. Uma forma equivalente é utilizar a função deviance definindo o intervalo pelos valores que satisfazem \(\mathrm{D}(\theta) = -2[\mathrm{l}(\theta)-\mathrm{l}(\hat{\theta})] \leq -2 \log(r)\). Esta é uma outra forma de considerar a verossimilhança relativa, agora em termos de diferença em log-verossimilhança. Neste caso a região de confiança pode ser definida como anteriormente ou valendo-se de propriedades frequentistas desta quantidade conforme veremos na sequência.
Em ambas abordagens surge o problema de que após definir o valor \(c^* = -2\log(r)\), é necessário encontrar as raízes da função de verossimilhança relativa ou da deviance que fornecem os limites do intervalo de confiança para um \(c^*\) especificado. Em geral vamos chamar o valor \(c^*\) ou equivalentemente \(r\) de ponto de corte. Encontrar as raízes da função comumente envolve métodos numéricos, uma vez que na maioria das situações práticas não é possível obter expressões fechadas para os limites do intervalo.
Dado esta restrição é comum fazer uma expansão em séries de Taylor para a \(\mathrm{l}(\theta)\) em torno de \(\hat{\theta}\) de forma a facilitar a obtenção do intervalo de confiança. Expandindo \(\mathrm{l}(\theta)\) em série de Taylor até segunda ordem em torno de \(\hat{\theta}\), resulta na seguinte equação,
\[
\mathrm{D}(\theta) = -2[\mathrm{l}(\theta)-\mathrm{l}(\hat{\theta})] = 2 \left\{\mathrm{l}(\hat{\theta}) - [ \mathrm{l}(\hat{\theta}) + (\theta - \hat{\theta})\mathrm{l}^{\prime}(\hat{\theta}) + \frac{1}{2}(\theta - \hat{\theta})^2 \mathrm{l}^{\prime \prime}(\hat{\theta})] \right\} .
\]
Como por definição do EMV \(\mathrm{l}^{\prime}(\hat{\theta}) = 0\), eliminando termos
a aproximação em série de Taylor, toma a seguinte forma quadrática e define a região
\[ \mathrm{D}(\theta) = - (\theta - \hat{\theta})^2 \mathrm{l}^{\prime \prime}(\hat{\theta}) \leq c^*. \]
que por sua vez, define intervalos de confiança da forma,
\[ \hat{\theta} \pm \sqrt{ \frac{c^*}{-\mathrm{l}^{\prime \prime}(\hat{\theta})}}. \]
Isto corresponde a fazer uma aproximação quadrática da função deviance, que torna o intervalo fácil de ser obtido. Estendendo para o caso de multiparâmetros, tem-se que uma região de confiança para \(\boldsymbol{\theta}\) é dada pelo conjunto \({ \boldsymbol{\theta} \in \Theta : \mathrm{D}(\boldsymbol{\theta}) \leq c^*}\). Portanto, as duas formas de interpretar o intervalo de confiança discutidas no caso uniparamétrico podem ser estendidas para o caso multiparamétrico, sem problemas. Novamente a questão que surge é a definição de um valor para \(c^*\). Pela abordagem frequentista é desejável que o intervalo tenha uma interpretação em termos de probabilidades ou frequência e isto é atingido através das propriedades assintóticas dos estimadores de máxima verossimilhança que serão apresentadas adiante, mas antes vamos materializar apresentar o terceiro objetivo da inferência estatística, ou seja, testes de hipóteses.
2.3 Testes de hipóteses
Nesta seção mostramos como diversos testes de hipóteses surgem naturalmente a partir da interpretação da função de verossimilhança.
Na definição acima, \(\chi\) denota o espaço amostral associado à amostra \(y_1, y_2, \ldots, y_n\). A função de decisão \(d\) divide o espaço amostral \(\chi\) em dois conjuntos, \[ A_0 = \{ ( y_1, \ldots, y_n \in \chi; d(y_1, \ldots, y_n) = a_0 \}\] e \[ A_1 = \{ ( y_1, \ldots, y_n \in \chi; d(y_1, \ldots, y_n) = a_1 \}\] onde \(A_0 \cup A_1 = \chi\) e \(A_0 \cap A_1 = \emptyset\). Como em \(A_0\) temos os pontos amostrais que levam à não rejeição de \(\mathrm{H_0}\), vamos chamar de \(A_0\) de região de não rejeição e, por analogia, \(A_1\) de região de rejeição de \(H_0\), também chamada de região crítica.
Um teste de hipótese pode resultar em um de dois tipos de erros. Tradicionalmente, esses dois tipos de erros recebem os nomes de erro Tipo I (\(\alpha\)) e erro Tipo II (\(\beta\)). O erro tipo I ocorre quando rejeitamos \(\mathrm{H_0}\) e esta é verdadeira. O erro Tipo II ocorre quando não rejeitamos \(\mathrm{H_0}\) e esta é falsa. Em termos de probabilidade temos, \[ \alpha = \mathrm{P}(Y \in A_1 | \theta_0) \quad \text{e} \quad \beta = \mathrm{P}(Y \in A_0 | \theta_1).\]
Note que \(\pi(\theta_1) = 1 - \beta\), e \(\beta\) é a probabilidade do erro Tipo II.
Estas definições tratam o teste de hipótese diretamente como uma função de decisão que quantifica a incerteza associada com cada possível decisão.
Uma forma mais intuitiva de construir um teste de hipótese é definir uma estratégia para definir se um particular valor, digamos, \(\theta_0\) é plausível para o parâmetro \(\theta\). Como já discutido a função de verossimilhança nos fornece exatamente a plausibilidade de um determinado valor do parâmetro ser o gerador da amostra realizada dada uma função de probabilidade ou densidade probabilidade especificada. Assim, usar a função de verossimilhança para decidir sobre a plausibilidade de \(\theta_0\) é natural.
Considere o gráfico da função de log-verossimilhança apresentado na Figura 2.1. Note que decidir sobre a plausibilidade do valor \(\theta_0\), consiste basicamente em medir o quanto longe ele está do valor mais plausível, ou seja, do EMV \(\hat{\theta}\). Baseado na Figura 2.1 fica claro que tal distância pode ser medida de pelo menos três formas diferentes: no eixo das ordenadas, no eixo das abscissas ou verificando se a inclinação da reta tangente a \(\theta_0\) é diferente de zero. Estas três formas de medir a distância entre \(\theta_0\) e \(\hat{\theta}\) levam a construção de três tipos de testes de hipóteses que serão discutidos nas próximos subseções.
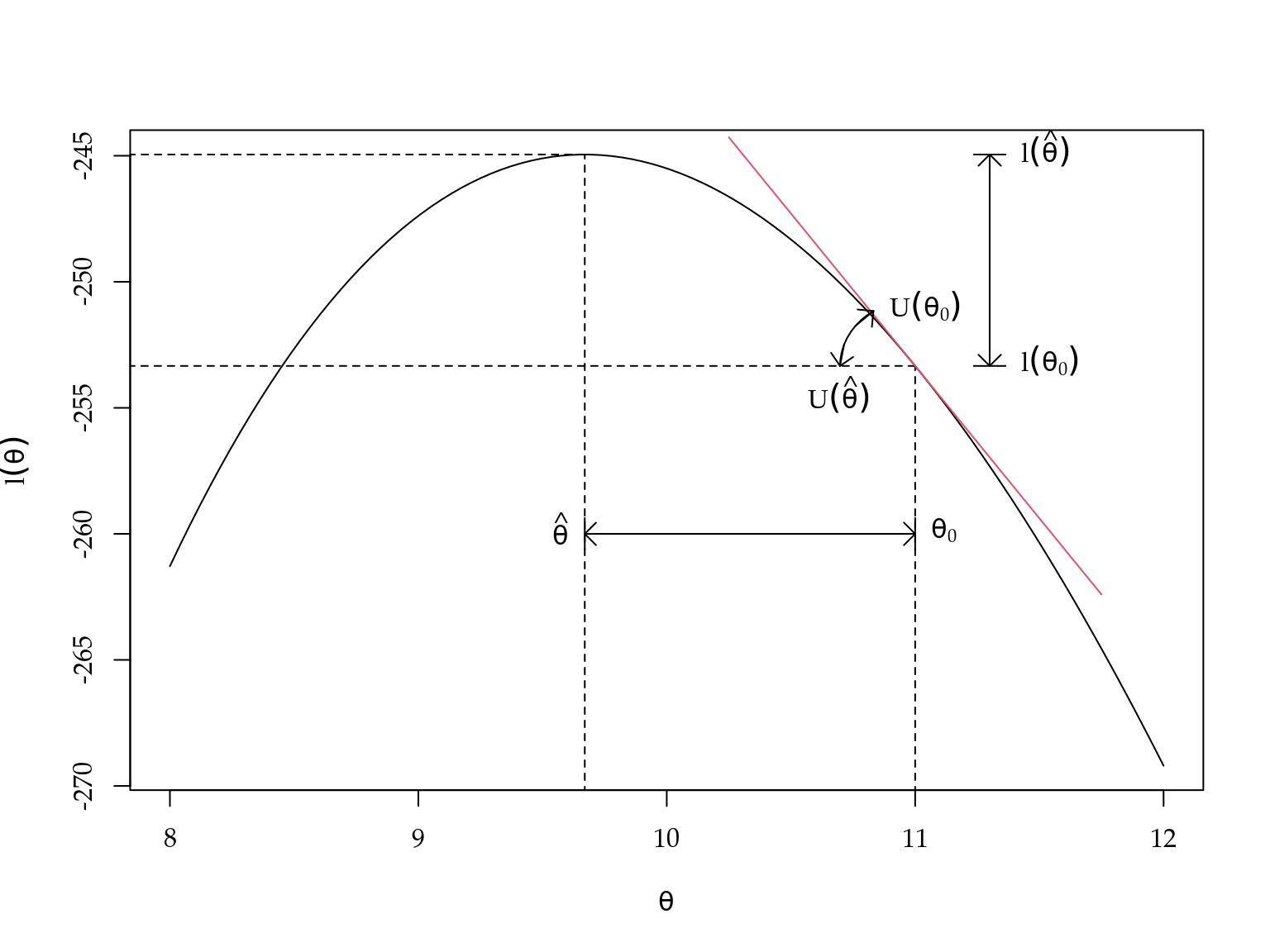
Figura 2.1: Diferentes formas de construir teste de hipótese baseado em verossimilhança.
2.3.1 Teste da razão de verossimilhança
Se decidirmos pela distância medida pelo eixo das ordenadas, somos levados ao teste da razão de verossimilhança.
Para testar \(\mathrm{H_0}: \theta = \theta_0\) versus \(\mathrm{H_1}: \theta \neq \theta_0\), suponha \(Y_1, \ldots, Y_n\) sejam iid \(f(\mathbf{y}|\theta)\), \(\hat{\theta}\) seja o EMV de \(\theta\), e \(f(\mathbf{y}|\theta)\) satisfaça as condições de regularidade. Desse modo, de acordo com \(\mathrm{H_0}\), pelo Teorema 2.5 à medida que \(n \to \infty\) \[ -2 \log \lambda(\underline{y}) \to \chi^2_1. \]
2.3.2 Teste de Wald
Por outro lado, se optamos pela distância no eixo das abscissas temos o chamado teste de Wald. Suponha que deseja-se testar a hipótese bilateral \(\mathrm{H_0} : \theta = \theta_0\) versus \(\mathrm{H_1} : \theta \neq \theta_0\).
Se \(\mathrm{H_0}\) for verdadeira, então \(\theta = \theta_0\) e \(Z_n\) convergem em distribuição para \(Z \sim N(0,1)\). Portanto, a probabilidade do Erro Tipo I, \(\mathrm{P}_{\theta_0}(\mathrm{Z_n} < - z_{\alpha/2} \quad \text{ou} \quad \mathrm{Z_n} > z_{\alpha/2}) \to \mathrm{P}(Z < -z_{\alpha/2} \quad \text{ou} \quad Z > z_{\alpha/2}) = \alpha\), e este é, assintoticamente, um teste de tamanho \(\alpha\). Em geral, um teste de Wald é um teste com base em uma estatística da forma, \[ \mathrm{Z_n} = \frac{\mathrm{W_n} - \theta_0}{\mathrm{S_n} } \] onde \(\theta_0\) é um valor hipotético do parâmetro \(\theta\), \(\mathrm{W_n}\) é um estimador de \(\theta\) e \(\mathrm{S_n}\) é o erro padrão de \(\mathrm{W_n}\), uma estimativa do desvio padrão de \(\mathrm{W_n}\). Se \(\mathrm{W_n}\) for o EMV para \(\theta\), então, \(\sqrt{\mathrm{I_O}(\hat{\theta})}\) é o erro padrão de \(\mathrm{W_n}\).
2.3.3 Teste escore
Por fim, podemos olhar para a inclinação da reta tangente no ponto \(\theta_0\) o que leva ao chamado teste escore. Lembre-se que a estatística escore é definida como \[\mathrm{U}(\theta) = \frac{\partial}{\partial \theta} \mathrm{l}(\theta | \boldsymbol{Y}).\]
Sabemos (ver 2.2) que para todo \(\theta\), \(\mathrm{E}_{\theta} (\mathrm{U}(\theta)) = 0\). Em particular, se estivermos testando \(\mathrm{H_0}: \theta = \theta_0\) e se \(\mathrm{H_0}\) for verdadeira, então \(\mathrm{U}(\theta)\) tem média \(0\). Além disso, \[ \mathrm{V}_{\theta}(\mathrm{U}(\theta)) = -\mathrm{E}_{\theta} \left( \frac{\partial^2 }{\partial \theta^2} \mathrm{l}(\theta | \boldsymbol{Y}) \right) = \mathrm{I_E}(\theta)\] ou seja, o número de informações é a variância da estatística escore.
2.4 Propriedades do EMV
Apesar de definirmos a função de verossimilhança como uma quantidade fixa avaliada em \(\mathbf{y}\), devemos lembrar que ela é baseada em apenas uma realização do vetor aleatório \(\mathbf{Y}\), sendo assim, estudar o comportamento probabilístico dos estimadores de máxima verossimilhança é de fundamental importância para definir suas propriedades probabilística e baseado nisto obter intervalos de confiança e testes de hipóteses com interpretações probabilísticas. Para isto, vamos precisar de mais algumas definições.
Definição 2.19 Função escore - Sendo \(\mathrm{l}(\boldsymbol{\theta}|\mathbf{y})\) a função de log-verossimilhança, o vetor escore é definido por \[ \mathrm{U}(\boldsymbol{\theta}) = \left( \frac{\partial \mathrm{l}(\boldsymbol{\theta})}{\partial \theta_1}, \ldots, \frac{\partial \mathrm{l}(\boldsymbol{\theta})}{\partial \theta_p}\right)^\top. \]
Note que a função escore nada mais é que o vetor gradiente da função de log-verossimilhança. Definimos as matrizes de informação observada e esperada, também chamada de matriz de informação de Fisher.
Definição 2.20 Matriz de informação observada - Sendo \(\mathrm{l}(\boldsymbol{\theta}|\mathbf{y})\) a função de log-verossimilhança, a matriz de informação observada é definida por \[ \mathrm{I}_O(\boldsymbol{\theta}) = \left[\begin{array}{cccc} - \frac{\partial^2 \mathrm{l}(\boldsymbol{\theta})}{\partial \theta_1^2} & \ldots & \ldots & -\frac{\partial^2 \mathrm{l}(\boldsymbol{\theta})}{\partial \theta_1 \partial \theta_p} \\ \vdots & \ddots & - \frac{\partial^2 \mathrm{l}(\boldsymbol{\theta})}{\partial \theta_i \partial \theta_j}& \vdots \\ \vdots & - \frac{\partial^2 \mathrm{l}(\boldsymbol{\theta})}{\partial \theta_j \partial \theta_i} & \ddots & \vdots \\ - \frac{\partial^2 \mathrm{l}(\boldsymbol{\theta})}{\partial \theta_p \partial \theta_1} & \ldots & \ldots & - \frac{ \partial^2 \mathrm{l}(\boldsymbol{\theta})}{\partial \theta_p^2} \end{array}\right]. \]
Definição 2.21 Matriz de informação esperada - Sendo \(\mathrm{l}(\boldsymbol{\theta}|\mathbf{y})\) a função de log-verossimilhança, a matriz de informação esperada é definida por
\[ \mathrm{I}_E(\boldsymbol{\theta}) = \left[\begin{array}{cccc} \mathrm{E} \left[- \frac{\partial^2 \mathrm{l}(\boldsymbol{\theta})}{\partial \theta_1^2} \right] & \ldots & \ldots & \mathrm{E} \left[-\frac{\partial^2 \mathrm{l}(\boldsymbol{\theta})}{\partial \theta_1 \partial \theta_p}\right] \\ \vdots & \ddots & \mathrm{E} \left[- \frac{\partial^2 \mathrm{l}(\boldsymbol{\theta})}{\partial \theta_i \partial \theta_j} \right]& \vdots \\ \vdots & \mathrm{E} \left[ - \frac{\partial^2 \mathrm{l}(\boldsymbol{\theta})}{\partial \theta_j \partial \theta_i}\right] & \ddots & \vdots \\ \mathrm{E} \left[- \frac{\partial^2 \mathrm{l}(\boldsymbol{\theta})}{\partial \theta_p \partial \theta_1}\right] & \ldots & \ldots & \mathrm{E} \left[- \frac{ \partial^2 \mathrm{l}(\underline{\theta})}{\partial \theta_p^2}\right] \end{array}\right]. \]
Duas propriedades importantes da função escore são apresentadas nos Teoremas a seguir.
Note que a variância do vetor \(\mathrm{U}(\boldsymbol{\theta})\) é a matriz com entradas \[ \left[\begin{array}{cccc} \mathrm{Cov}(\mathrm{U_1}, \mathrm{U_1}) & \ldots & \ldots & \mathrm{Cov}(\mathrm{U_1},\mathrm{U_d}) \\ \vdots & \ddots & \mathrm{Cov}(\mathrm{U_i}, \mathrm{U_j}) & \vdots \\ \vdots & \mathrm{Cov}(\mathrm{U_j}, \mathrm{U_i}) & \ddots & \vdots \\ \mathrm{Cov}(\mathrm{U_d},\mathrm{U_1}) & \ldots & \ldots & \mathrm{Cov}(\mathrm{U_d}, \mathrm{U_d}) \end{array}\right]. \] onde \(\mathrm{Cov}(\mathrm{U_i}, \mathrm{U_i}) = \mathrm{V}(\mathrm{U_i})\). Uma propriedade importante de \(\mathrm{I}_O(\boldsymbol{\hat{\theta}})\) e \(\mathrm{I}_E(\boldsymbol{\hat{\theta}})\) é que elas são matrizes definida positiva, as quais mensuram a curvatura observada/esperada da superfície de log-verossimilhança. Com estas definições, pode-se escrever a função deviance aproximada para um vetor de parâmetros da seguinte forma: \[ \mathrm{D}(\boldsymbol{\theta}) \approx (\boldsymbol{\theta} - \boldsymbol{\hat{\theta}})^\top \mathrm{I_O}(\boldsymbol{\hat{\theta}})(\boldsymbol{\theta} - \boldsymbol{\hat{\theta}}) . \] Assim \(\mathrm{D}(\boldsymbol{\theta})\) é não negativa uma vez que \(\mathrm{I_O}(\boldsymbol{\hat{\theta}})\) é uma matriz positiva definida. Uma vez definidas as quantidades envolvidas, estamos aptos a enunciar o teorema a seguir.
Teorema 2.4 Distribuição assintótica do EMV - Para um problema de estimação regular, no limite com \(n \to \infty\), se \(\boldsymbol{\theta}\) é o verdadeiro vetor de parâmetros, então \[\hat{\boldsymbol{\theta}} \sim NM_p(\boldsymbol{\theta}, \mathrm{I_E}(\boldsymbol{\theta})^{-1}),\] ou seja, a distribuição assintótica de \(\hat{\boldsymbol{\theta}}\) é uma normal multivariada com matriz de variância/covariância dada pela inversa da matriz de informação esperada.
Corolário 2.1 Qualquer termo assintóticamente equivalente a \(\mathrm{I_E}(\boldsymbol{\theta})\) pode ser usado no Teorema 2.4. Assim, \[ \hat{\boldsymbol{\theta}} \sim NM_p(\boldsymbol{\theta}, \mathrm{I_E}^{-1}(\boldsymbol{\hat{\theta}}))\] \[ \hat{\boldsymbol{\theta}} \sim NM_p(\boldsymbol{\theta}, \mathrm{I_O}^{-1}(\boldsymbol{\theta}))\] \[ \hat{\boldsymbol{\theta}} \sim NM_p(\boldsymbol{\theta}, \mathrm{I_O}^{-1}(\boldsymbol{\hat{\theta}})).\]
Teorema 2.5 Distribuição assintótica da deviance - Para um problema de estimação regular, no limite com \(n \to \infty\), se \(\boldsymbol{\theta}\) é o verdadeiro valor do parâmetro, então \[ \mathrm{D}(\boldsymbol{\theta}) = -2[\mathrm{l}(\boldsymbol{\theta})-\mathrm{l}(\hat{\boldsymbol{\theta}})] \sim \chi^2_d \] ou seja, a função deviance segue uma distribuição qui-Quadrado com \(p\) graus de liberdade, onde \(p\) é a dimensão do vetor \(\boldsymbol{\theta}\).
De acordo com os teoremas apresentados, podemos chegar a algumas das principais propriedades dos estimadores de máxima verossimilhança:
- O estimador de máxima verossimilhança \(\hat{\boldsymbol{\theta}}\) de \(\boldsymbol{\theta}\) é assintóticamente não-viciado, isto é, \(\mathrm{E}(\hat{\boldsymbol{\theta}}) \to \boldsymbol{\theta}\).
- Assintóticamente \(\mathrm{V}(\hat{\boldsymbol{\theta}}) \to \mathrm{I_E}^{-1}(\boldsymbol{\theta})\), o qual por uma versão multivariada do limite de Cramér-Rao é o melhor possível, mostrando que o EMV é eficiente para o vetor \(\boldsymbol{\theta}\), ao menos para grandes amostras.
- Denote \(\mathrm{J} = \mathrm{I_E}^{-1}(\boldsymbol{\theta})\), então \(\mathrm{V}(\hat{\boldsymbol{\theta}}) = \mathrm{J}\), sendo que, \(\mathrm{J}\) é uma matriz simétrica e definida positiva, com elementos \(\mathrm{J_{ij}} = \mathrm{Cov}(\hat{\boldsymbol{\theta}}_i, \hat{\boldsymbol{\theta}}_j)\) então \(\mathrm{J_{ii}}\) é a variância de \(\hat{\boldsymbol{\theta}}_i\). Denota-se \(\mathrm{J_{ii}}^{\frac{1}{2}}\) o desvio padrão de \(\hat{\boldsymbol{\theta}}_i\).
- Podemos construir intervalos de \(100(1-\alpha)\%\) de confiança para \(\theta_i\) na forma \(\hat{\theta}_i \pm z_{\frac{\alpha}{2}} \mathrm{J_{ii}}^{\frac{1}{2}}\). Intervalos desta forma serão denominados, intervalos de Wald ou baseados em aproximação quadrática da verossimilhança. Importante notar que estes intervalos coincidem com os obtidos baseado em aproximação por Série de Taylor de segunda ordem da função deviance.
- Para regiões de confiança baseados na deviance considera-se $[ : () c^*] $, para algum valor \(c^*\) a ser especificado. Pode-se escolher \(c^*\) baseado em justificativas assintóticas de que \(\mathrm{D}(\boldsymbol{\theta}) \sim \chi^2_p\) é uma escolha razoável para \(c^* = c_{\alpha}\) com \(\mathrm{P}(\chi^2_d \ge c_{\alpha}) = \alpha\), por exemplo se \(\alpha = 0.05\), então \(c_{\alpha} = 3.84\). Isto gera uma região de \(100(1 - \alpha)\%\) de confiança. Estes intervalos serão denominados de intervalos deviance.
De acordo com as propriedades apresentadas tem-se duas formas básicas de construir intervalos de confiança. A primeira mais simples é baseada na aproximação quadrática da log-verossimilhança e a segunda utilizando diretamente a função deviance obtida com os dados. A segunda opção é em geral mais trabalhosa computacionalmente, uma vez que usualmente gera uma equação não linear que precisa ser resolvida numericamente. A primeira opção é bastante direta, uma vez obtida a matriz de segundas derivadas basta invertê-la e tirar a raiz dos termos da diagonal para se obter o intervalo de confiança para cada parâmetro, marginalmente. Esta abordagem é muito simples mas apresenta limitações. Restrições naturais no espaço paramétrico como, por exemplo, para parâmetros de variância e correlação não são respeitadas e podem resultar em limites absurdos, com limite(s) do intervalo fora do espaço paramétrico. Os intervalos serão sempre simétricos ao aproximar a verossimilhança por uma forma quadrática, o que normalmente não produz resultados adequados para parâmetros de variância e correlação. Em modelos com efeitos aleatórios há um interesse natural nos parâmetros de variância, precisão e correlação. Testar a significância de tais efeitos utilizando as variâncias associadas às estimativas que indexam o modelo podem produzir resultados imprecisos. Logo, esta abordagem é limitida em classes mais gerais de modelos estatísticos.
A segunda opção resulta em uma região conjunta para o caso de dois ou mais parâmetros, enquanto que pela aproximação é possível obter um intervalo marginal para cada parâmetro, porém baseado em uma aproximação quadrática da superfície de log-verossimilhança. Este tipo de representação é a mais desejável para inferência, porém não pode ser obtida diretamente apenas com o Teorema 2.5. Por exemplo, suponha que tem-se interesse em um determinado componente do vetor de parâmetros, digamos \(\theta_i\). A partir da aproximação quadrática podemos facilmente construir um intervalo de confiança, tendo como \(\hat{\theta}_I\) e \(\hat{\theta}_S\) o seu limite inferior e superior, respectivamente. Pelo Teorema 2.5 para o caso em que a dimensão de \(\boldsymbol{\theta}\) é maior que um, não temos um intervalo desta forma mas sim uma região, o que apesar de mais informativa tem menor apelo prático e apresenta dificuldades de interpretação. Uma forma intuitiva de obter um intervalo da forma \(\hat{\theta}_I\) e \(\hat{\theta}_S\) é fixar o restante do vetor de parâmetros nas suas estimativas de máxima verossimilhança e obter os limites em uma direção de cada vez. Esta abordagem tem uma clara restrição que é não levar em consideração a incerteza associada ao restante do vetor de parâmetros para a construção do intervalo.
Temos um método simples via aproximação quadrática, porém que não funciona bem quando a superfície de log-verossimilhança é assimétrica. Por outro lado, o método baseado na função deviance não apresenta esta restrição mas fornece regiões de confiança conjuntas, e não diretamente limites \(\hat{\theta}_I\) e \(\hat{\theta}_S\) para cada parâmetro. Duas abordagens básicas para este problema podem ser consideradas: a primeira é fazer uma reparametrização do modelo nos parâmetros que apresentam forte assimetria ou são restritos, para torná-los irrestritos e aproximadamente simétricos, obter a variância baseada na aproximação quadrática nesta reparametrização e depois converter para a escala original. Quando este procedimento é satisfatório o custo computacional é baixo. Uma outra opção é construir uma nova verossimilhança que não dependa dos outros parâmetros, de forma que podemos atuar como no caso uniparamétrico. Estas duas alternativas serão discutidas na próxima seção.
2.5 Reparametrização e verossimilhança perfilhada
Considere o problema de obter a estimativa pontual e intervalar para um parâmetro de interesse \(\phi = \mathrm{g}(\boldsymbol{\theta})\), onde \(\mathrm{g}(\cdot)\) é uma função e, desde que \(\mathrm{L}(\phi) = \mathrm{L}( \mathrm{g}(\boldsymbol{\theta}))\), a função de verossimilhança para \(\phi\) é obtida da função de verossimilhança de \(\boldsymbol{\theta}\) por uma transformação de escala. Consequentemente, como \(\hat{\phi} = \mathrm{g}(\boldsymbol{\hat{\theta}})\), quando o intervalo de confiança digamos \(\hat{\theta}_I\) e \(\hat{\theta}_S\) for obtido diretamente pela função de verossimilhança, log-verossimilhança ou deviance, o intervalo para \(\phi\) pode ser obtido simplesmente transformando os limites obtidos para \(\theta\), no caso unidimensional. Esta propriedade é conhecida como invariância do estimador de máxima verossimilhança. Porém, quando o intervalo for obtido pela aproximação quadrática isso não é válido e um Teorema adicional é necessário para esta transformação.
Teorema 2.6 Considere obter um intervalo de confiança para \(\phi = \mathrm{g}(\boldsymbol{\theta})\) por invariância temos que \(\hat{\phi} = \mathrm{g}(\hat{\boldsymbol{\theta}})\) e a variância de \(\hat{\phi}\) é dada por \[ \mathrm{V}(\hat{\phi}) = \mathrm{V}( \mathrm{g}(\hat{\boldsymbol{\theta}})) = \nabla \mathrm{g}(\hat{\boldsymbol{\theta}})^\top \mathrm{I_E}(\hat{\boldsymbol{\theta}})^{-1} \nabla \mathrm{g}(\hat{\boldsymbol{\theta}}) \] com \[ \nabla \mathrm{g}(\hat{\boldsymbol{\theta}}) = \left( \frac{\partial \mathrm{g}(\hat{\boldsymbol{\theta}})}{\partial \theta_1}, \ldots, \frac{\partial \mathrm{g}(\hat{\boldsymbol{\theta}})}{\partial \theta_d} \right)^\top. \]
A partir do Teorema 2.6 é imediato o seguinte teorema.
Pelo Teorema 2.7, podemos construir intervalos de confiança da mesma forma anterior, porém usando a nova matriz de variância e covariância ponderada pelo gradiente da função \(\mathrm{g}(\cdot)\), e assim passar de uma reparametrização para outra torna-se uma tarefa trivial. Apesar deste procedimento ser bastante útil, nem sempre é fácil encontrar uma transformação \(\mathrm{g}(\cdot)\) que torne a log-verossimilhança simétrica. A forma mais efetiva de construir intervalos de confiança para parâmetros de difícil estimação é o intervalo baseado em perfil de verossimilhança.
Seja \(\boldsymbol{\theta} = (\boldsymbol{\phi}^\top, \boldsymbol{\lambda}^\top)^\top\), o vetor de parâmetros particionado nos vetores \(\boldsymbol{\phi}\) e \(\boldsymbol{\lambda}\), vamos chamar a primeira componente de interesse e a segunda de incômodo, no sentido que desejamos intervalos ou regiões de confiança para \(\boldsymbol{\phi}\), que pode ser apenas um escalar. Seja \(\mathrm{L}(\boldsymbol{\phi}, \boldsymbol{\lambda})\) a verossimilhança para \(\boldsymbol{\phi}\) e \(\boldsymbol{\lambda}\). Denota-se \(\hat{\boldsymbol{\lambda}}_{\phi}\) a estimativa de máxima verossimilhança de \(\boldsymbol{\lambda}\) para dado um valor para \(\boldsymbol{\phi}\).
Definição 2.22 Verossimilhança perfilhada - A verossimilhança perfilhada de \(\boldsymbol{\phi}\) é definida por \[ \mathrm{L}(\boldsymbol{\phi}) = \mathrm{L}(\boldsymbol{\phi}, \hat{\boldsymbol{\lambda}}_{\phi}) \]
A forma apresentada na definição 2.22 sugere um procedimento de maximização em duas etapas. A primeira consiste em obter \(\hat{\boldsymbol{\lambda}}_{\phi}\) que maximiza \(\mathrm{l}(\boldsymbol{\phi}, \boldsymbol{\lambda}) = \log \mathrm{L}(\boldsymbol{\phi}, \boldsymbol{\lambda})\) com respeito a \(\boldsymbol{\lambda}\) supondo \(\boldsymbol{\phi}\) fixo. A seguir maximiza-se \(\mathrm{l}(\boldsymbol{\phi})\). Assim, uma região ou intervalo de confiança para \(\boldsymbol{\phi}\) pode ser obtida usando que \[ \mathrm{D}(\boldsymbol{\phi}) = -2[\mathrm{l}(\boldsymbol{\phi})-\mathrm{l}(\hat{\boldsymbol{\phi}})] \sim \chi^2_d \] onde \(d\) é a dimensão de \(\boldsymbol{\phi}\). Note que esta forma de construção não usa a aproximação em séries de Taylor e portanto pode resultar em intervalos assimétricos. Porém, é cara computacionalmente, uma vez que precisamos resolver numéricamente uma equação não-linear que para cada avaliação necessita de um algoritmo numérico de maximização.
Neste Capítulo apresentamos uma série de definições e propriedades do procedimento de inferência baseado na função de verossimilhança. Os exemplos de ilustração foram o mais simples possível, porém mesmo nestes casos a necessidade do uso de métodos numéricos ficou bastante evidente. No próximo capítulo vamos discutir uma série de exemplos que em geral tem soluções analiticas, porém vamos resolvê-los também numéricamente para ilustrar as principais ideias e desafios relacionados a obtenção de estimadores pontuais, intervalares e testes de hipóteses.
2.6 Estimação pontual
Neste exemplo vamos considerar um problema para o qual o estimador de máxima verossimilhança pode ser obtido analiticamente, porém vamos explorar diversas formas de obtê-lo também numéricamente utilizando métodos numéricos disponíveis em R. Vamos começar mostrando quatro representações da função de verossimilhança. Para facilitar a notação vamos omitir a dependência da função de verossimilhança em \(\mathbf{y}\), ou seja, \(\mathrm{L}(\boldsymbol{\theta}|\mathbf{y}) = \mathrm{L}(\boldsymbol{\theta})\), seguindo de forma análoga para a log-verossimilhança e funções obtidas apartir destas.
O modelo que vamos considerar é o modelo Poisson. Sendo assim, seja \(Y_i \sim P(\theta)\) com \(i = 1, \ldots, n\), variáveis aleatórias independentes e denote \(\overline{y} = \sum_{i=1}^n y_i/n\). A função de verossimilhança é o produto das \(n\) distribuições de Poisson com parâmetro \(\theta\) que neste caso é assumido comum a todas as variáveis aleatórias e desconhecido. A função de verossimilhança é dada pela expressão a seguir, notando-se que, observada uma determinada amostra, o termo no denominador é uma constante.
\[ \mathrm{L}(\theta) = \prod_{i=1}^n \frac{\exp\{-\theta\} \theta^{y_i}}{y_i!} = \frac{\exp\{-n \theta\} \theta^{\sum_{i=1}^n y_i}}{\prod_{i=1}^n y_i !}. \]
Um representação alternativa é a função de verossimilhança relativa. Sendo, \(\hat{\theta}\) o EMV para \(\theta\) a função de verossimilhança relativa é dada por \(\mathrm{LR}(\theta) = \frac{\mathrm{L}(\theta)}{\mathrm{L}(\hat{\theta})}\) que para esse exemplo, após uma série de simplificações, tem a seguinte expressão \[ \mathrm{LR}(\theta) = \exp\{-n(\theta-\hat{\theta})\} (\theta/\hat{\theta})^{n \overline{y}}. \]
A verossimilhança relativa assume sempre valores no intervalo unitário o que facilita a construção e visualização de gráficos. Note ainda que nesta representação o termo constante no denominador é cancelado. Uma vez que o termo constante envolve o cálculo de fatoriais o fato de cancelar é conveniente computationalmente, porque o cálculo de fatoriais é altamente suceptível a problemas numéricos.
Outra possibilidade é usar a função de log-verossimilhança \(\mathrm{l}(\theta) = \log \mathrm{L}(\theta)\) que normalmente é preferida para se trabalhar analítica e computacionalmente. Para o exemplo da distribuição de Poisson, a expressão é como se segue com o último termo constante para uma determinada amostra.
\[ \mathrm{l}(\theta) = - n \theta + n \overline{y} \log(\theta) - \sum_{i=1}^n \log(y_i!). \]
Por fim, podemos ainda utilizar a função deviance dada por, \(\mathrm{D}(\theta) = -2 \mathrm{LR}(\theta) = 2\{ \mathrm{l}(\hat{\theta}) - \mathrm{l}(\theta) \}\), que é comumente reportada por algoritmos e utilizada na obtenção de intervalos de confiança e testes de hipóteses devido as suas propriedades assintóticas, ver Teorema 2.5. Assim como na verossimilhança relativa, a sua expressão elimina o termo constante ficando na forma:
\[ \mathrm{D}(\theta) = 2 n \{(\hat{\theta}-\theta)-\overline{y} \log(\hat{\theta}/\theta)\}. \]
Neste caso o estimador de máxima verossimilhança para \(\theta\) pode ser encontrado analiticamente maximizando a função de log-verossimilhança. O primeiro passo é encontrar a verossimilhança e a log-verossimilhança.
\[\begin{align*} \mathrm{L}(\theta) &= \prod_{i=1}^n \frac{ \exp\{-\theta\} \theta^{y_i}}{y_i !} = \frac{ \exp\{-n \theta\} \theta^{\sum_{i=1}^n y_i}}{\prod_{i=1}^n y_i !} \\ \mathrm{l}(\theta) &= - n \theta + (\sum_{i=1}^n y_i) \log (\theta) - \sum_{i=1}^n \log y_i ! \\ \end{align*}\]
Para encontrar o ponto de máximo da log-verossimilhança vamos usar a estratégia padrão de cálculo diferencial que consiste em encontrar a primeira derivada e a sua raiz. Usando a nossa terminologia vamos obter a função escore e encontrar o ponto onde ela cruza o eixo das abscissas.
\[\begin{align*} \mathrm{U}(\theta) &= - n + \frac{\sum_{i=1}^n y_i}{\theta} \\ \end{align*}\]
Resolvendo a equação, temos \[\begin{align*} \mathrm{U}(\hat{\theta}) &= - n + \frac{\sum_{i=1}^n y_i}{\hat{\theta}} = 0 \\ \hat{\theta} &= \frac{\sum_{i=1}^n y_i}{n} = \overline{y}. \end{align*}\]
Por fim, podemos também obter a segunda derivada e verificar se ela é negativa para confirmar que o ponto encontrado é realmente um ponto de máximo
\[\begin{align*} \mathrm{H}(\theta) = -\frac{ \sum_{i=1}^n y_i}{ \theta^2}. \end{align*}\]
Dado que \(y_i\) e \(\theta\) são estritamente positivos a segunda derivada \(\mathrm{H}(\theta)\) é negativa, mostrando que o ponto obtido é de máximo ao menos local.
Para ilustrar graficamente as diferentes representações da verossimilhança
vamos simular uma amostra da distribuição de Poisson com parâmetro \(\theta = 10\).
Note que vamos fixar a semente usando a função set.seed() para que os
resultados sejam reproduzíveis.
set.seed(20)
y <- rpois(20, lambda = 10)A Figura 2.2, apresenta os gráficos dessas quatro formas de visualização da função de verossimilhança para os dados simulados.
Utilizamos a função definida no código 2.1 que permite
escolher a representação desejada da verossimilhança. As verossimilhanças relativa e deviance requerem que o valor da verossimilhança maximizada seja informado no argumento
maxlogL, que é constante para uma determinada amostra. Deixamos este cálculo fora da função para evitar que esta quantidade constante seja recalculada nas sucessivas avaliações da função. Para facilitar a obtenção dos gráficos definimos a função na forma vetorizada utilizando sapply(). Assim, a função pode receber um vetor de valores para o parâmetro.
veroPois <- function(par, dados, tipo, maxlogL){
tipo = match.arg(tipo, choices=c("L","LR","logL","dev"))
ll <- sapply(par, function(p) sum(dpois(dados, lambda=p, log=TRUE)))
return(switch(tipo, "L" = exp(ll),
"LR" = exp(ll-maxlogL),
"logL" = ll,
"dev" = 2*(maxlogL-ll)))} Os comandos a seguir mostram a obtenção da log-verossimilhança maximizada \(\mathrm{l}(\hat{\theta})\) e a chamada para obter o gráfico da função deviance \(\mathrm{D}(\theta)\). Para os demais gráficos basta alterar os valores do
argumento tipo.
mll <- sum(dpois(y, lambda = mean(y), log = TRUE))
curve(veroPois(x, dados = y, tipo = "dev", maxlogL = mll), 8, 11,
ylab=expression(D(theta)), xlab=expression(theta))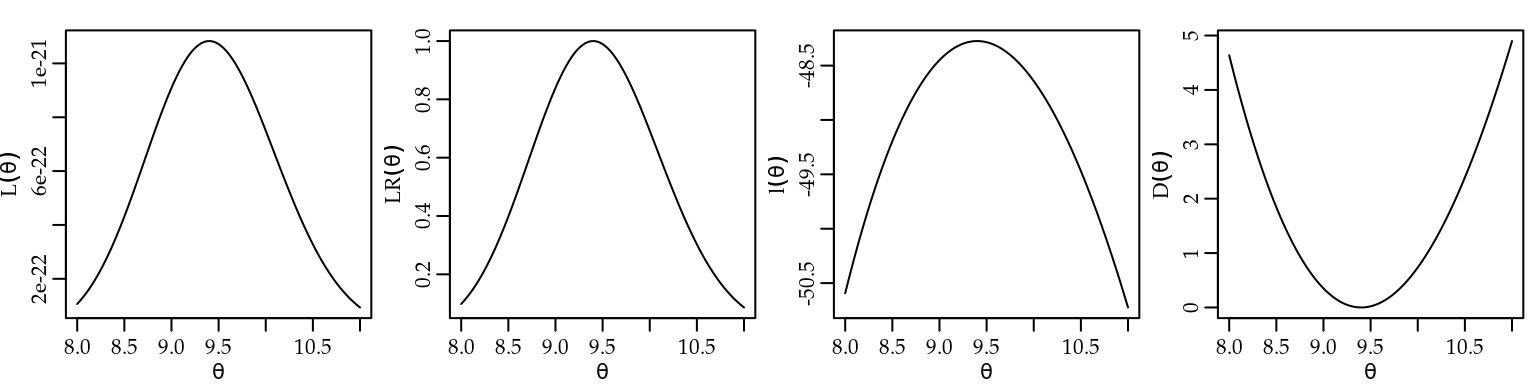
Figura 2.2: Diferentes formas de visualizar a função de verossimilhança - Distribuição Poisson.
Apesar das quatro formas serem equivalentes a forma usual para encontrar o estimador de máxima verossimilhança é a log-verossimilhança. De forma geral, cálculos analíticos com a função de verossimilhança \(\mathrm{L}(\theta)\) podem ser mais trabalhosos e sua computação mais sensível a valores pequenos o que pode gerar problemas numéricos, por exemplo excedendo a capacidade de representação de números. Por outro lado, a verosimilhança relativa e a deviance requerem o valor da função de verosimilhança avaliado na estimativa o que pode ser complicado em alguns casos.
Embora neste exemplo o EMV possa ser encontrado analiticamente, vamos
ilustrar a sua obtenção usando métodos numéricos comumente utilizados
para encontrar o EMV em situações mais desafiadoras.
Mas antes disto vamos redefinir a função de verossimilhança escrita
agora como função da estatística suficiente calculada com os valores da amostra.
Definimos \(\mathrm{l}(\theta)\) como opção default.
O argumento amostra deve receber uma lista com o tamanho e a soma dos
termos da amostra. Omitimos em \(\mathrm{L}(\theta)\) e \(\mathrm{l}(\theta)\) o termo que não depende do parâmetro. \(\mathrm{LR}(\theta)\) e \(\mathrm{D}(\theta)\) não se alteram pois os termos se cancelam em seu cálculo.
veroPois <- function(par, amostra, tipo="logL", maxlogL){
tipo = match.arg(tipo, choices=c("L","LR","logL","dev"))
ll <- with(amostra, -n*par + soma * log(par))
return(switch(tipo, "L" = exp(ll),
"LR" = exp(ll-maxlogL),
"logL" = ll,
"dev" = 2*(maxlogL-ll)))} Comandos equivalentes aos anteriores para obtenção do gráfico são como a seguir.
am <- list(n=length(y), soma=sum(y))
emv <- mean(y)
mll <- veroPois(emv, amostra=am, tipo="logL")
curve(veroPois(x, amostra=am, tipo="dev", maxlogL=mll), 8, 11,
ylab=expression(D(lambda)), xlab=expression(lambda))Para ilustrar a obtenção da estimativa do parâmetro por métodos numéricos vamos
considerar as seguintes opções:
- solução da equação de estimação (função escore) \(\mathrm{U}(\theta) = 0\) por um método sem uso de gradientes (Brent) e por um método com uso apenas do gradiente (gradiente descendente) e com o uso de gradiente e hessiano (Newton-Raphson);
- maximização direta da função de log-verossimilhança usando maximizadores numéricos.
Começamos escrevendo uma função para avaliar a função escore.
UPois <- function(theta, amostra){
return(with(amostra, n - soma/theta))
}Para obter a estimativa utilizamos inicialmente a função uniroot() que implementa o método de Brent para encontrar a raiz de uma equação não linear. Note que para usar este algoritmo precisamos definir um intervalo de busca através do argumento interval. Neste caso, especificamos o intervalo entre o menor e o maior valor observado na amostra, conforme mostra o código abaixo.
am <- list(n=length(y), soma=sum(y))
emv <- mean(y)
uniroot(UPois, interval = range(y), amostra = am)$root## [1] 9.4Um dos algoritmos mais utilizado para encontrar a raiz de uma equação não-linear é o do gradiente descendente que é muito simples de implementar e entender. Basicamente, a derivada da função nos fornece a direção de maior descida, então basta andar nesta direção a um passo de tamanho digamos, \(\alpha\) o que leva a seguinte equação de iteração
\[ \theta^{r+1} = \theta^{r} - \alpha \mathrm{U}(\theta^r), \] onde \(\alpha\) é um parâmetro de tuning que precisa ser escolhido cuidadosamente e caso a caso. O código 2.4 é uma implementação minima deste método e vamos usá-la neste exemplo e na sequência do livro.
grad_des <- function(U, x1, alpha, max_iter = 100, tol = 1e-04, ...) {
sol <- c(); sol[1] <- x1
for(i in 1:max_iter) {
sol[i+1] <- sol[i] - alpha*U(sol[i], ...)
if(abs(U(sol[i+1], ...)) < tol) break
}
return(sol)
}O método de Newton-Raphson é uma outra opção muito popular para a solução de equações não-lineares, utilizando uma expansão em séries de Taylor de \(\mathrm{U}(\theta)\), resolve a equação a seguir até que algum critério de convergência seja atingido
\[\theta^{r+1} = \theta^{r} + \frac{\mathrm{U}(\theta^r)}{\mathrm{H}(\theta^r)}.\]
Note que a única diferença em relação ao método do gradiente descendente é que o parâmetro de tuning \(\alpha\) é substituído por \(\frac{1}{\mathrm{H}(\theta)}\), ou seja, pelo recíproco do Hessiano. Para implementar o algorítmo precisamos primeiro definir a função \(\mathrm{H}(\theta) = \mathrm{U}^{\prime}(\theta)\).
HPois <- function(theta, amostra){
return(-amostra$soma/theta^2)
}Uma variante do método é utilizar \(\mathrm{H}(\theta) = -\mathrm{I_E}(\theta)\), conhecido como Fisher scoring onde \(\mathrm{I_E}(\theta) = \mathrm{E}(\mathrm{H}(\theta))\) é conhecida como matriz de informação de Fisher. O método de Newton-Raphson é implementado no código 2.6
newton <- function(U, H, x1, tol = 1e-04, max_iter = 10, ...) {
solucao <- c()
solucao[1] <- x1
for(i in 1:max_iter) {
solucao[i+1] = solucao[i] + U(solucao[i], ...)/H(solucao[i], ...)
if( abs(solucao[i+1] - solucao[i]) < tol) break
}
return(solucao)
}Finalmente, podemos usar os dois métodos para encontrar o EMV.
iter_gd <- grad_des(U = UPois, x1 = 5, alpha = 0.5, amostra = am)
iter_nr <- newton(U = UPois, H = HPois, x1 = 5, amostra = am)
# EMV método Gradiente descendente
round(iter_gd[length(iter_gd)], 4)## [1] 9.4# EMV método Newton-Raphson
round(iter_nr[length(iter_nr)], 4)## [1] 9.4No exemplo a estimativa \(\hat{\theta}\) foi obtida em 7 iterações pelo algoritmo gradiente descendente e 6 pelo método de Newton-Raphson.
Em ambos os casos a estimativa foi \(9.4\) como esperado e já obtido pela função uniroot().
Existem ainda funções no R que implementam estes algoritmos de forma mais genérica, incluindo a opção de usar derivadas obtidas numéricamente para modelos em que não há expressões fechadas para estas funções.
Vimos diversas alternativas para resolver a equação escore e encontrar o EMV. Uma outra opção é maximizar diretamente a função de log-verosimilhança \(\mathrm{l}(\theta)\).
Para o caso de um único paramêtro utilizamos a função optimize()
que utiliza o algoritmo de Brent, porém diversas outras funções estão disponíveis
no R e em seus pacotes extras, sendo mais comum o uso da função optim().
Abaixo ilustramos o uso da função optimize() para maximizar a log-verossimilhança.
unlist(optimize(veroPois, int=range(y), maximum=TRUE, amostra=am)[1:2])## maximum objective
## 9.4 233.3Obviamente, todas as abordagens levam a obtenção do mesmo valor para a estimativa de máxima verossimilhança.
Como o estimador de máxima verossimilhança é uma função de uma variável aleatória ele também é uma variável aleatória. Conforme as propriedades apresentadas no Capítulo 2 o EMV é assintoticamente não-viciado e sua distribuição amostral é assintóticamente gaussiana. Para exemplificar estas propriedades vamos fazer um pequeno estudo de simulação. O objetivo é ilustrar como se comporta o viés e a distribuição do EMV conforme aumenta-se o tamanho da amostra. Para isto, simulamos \(1000\) conjuntos de dados de acordo com o modelo Poisson com \(\theta = 3.5\) e \(\theta = 10\). Vamos retirar amostras de tamanho \(5, 50\) e \(100\) e para cada amostra calcular o EMV.
A Figura 2.3 apresenta os resultados deste estudo de simulação. Pelas propriedades do EMV temos que \(\hat{\theta} \sim \mathrm{N}(\theta, \frac{\theta}{n})\). Na Figura 2.3 sobrepomos o histograma das estimativas obtidas nas simulações com a distribuição assintótica (normal).
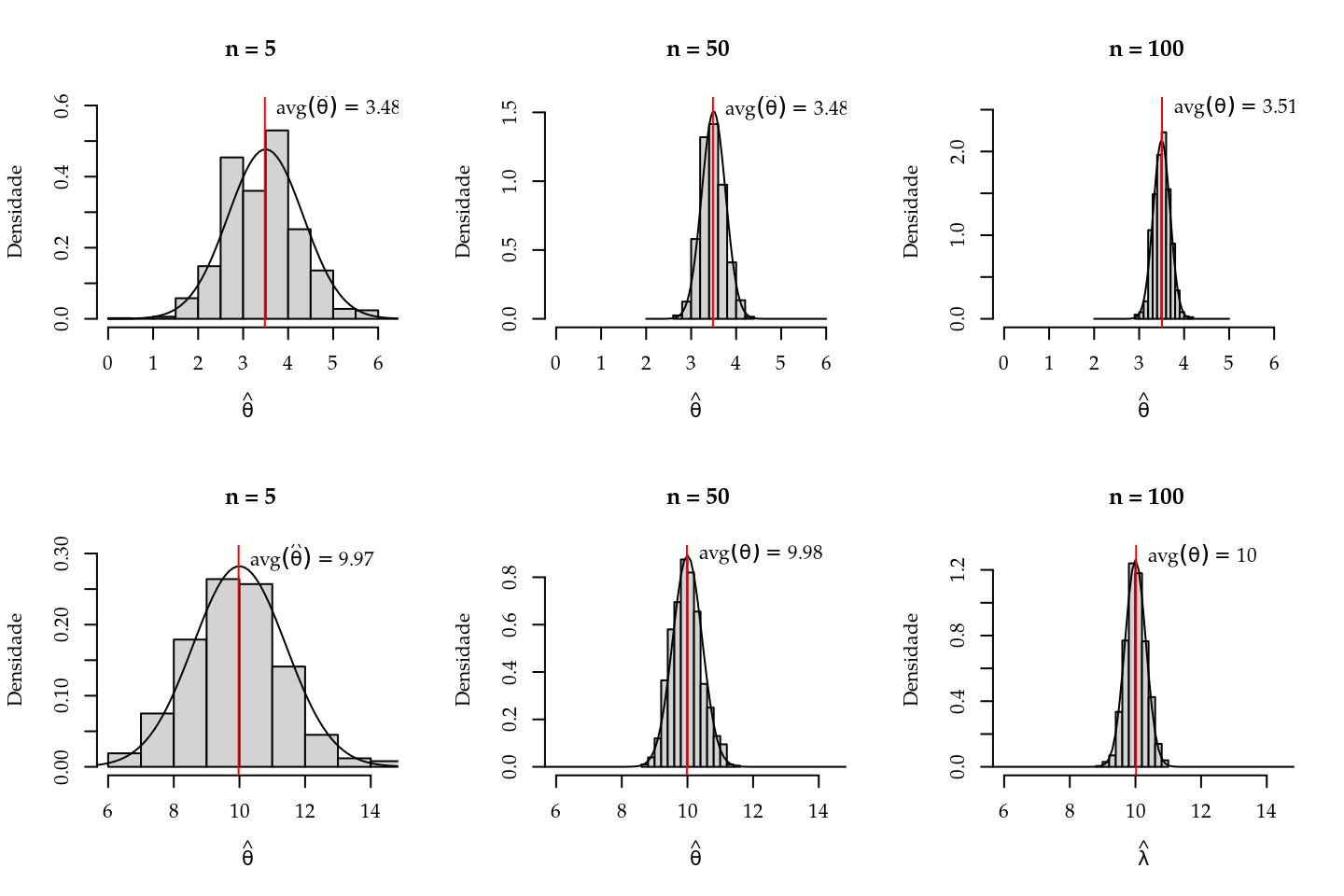
Figura 2.3: Illustração da distribuição assintótica do estimador de máxima verossimilhança- Distribuição Poisson.
Como é possível visualizar na Figura 2.3 a distribuição empírica apresenta um comportamento muito próximo da distribuição teórica, mesmo para valores pequenos de \(\theta\) e amostras pequenas \(n = 5\) e \(n = 50\). De forma geral, o viés vai diminuindo conforme a amostra aumenta. Nos gráficos a notação \(avg(\hat{\theta})\) representa a média das estimativas de máxima verossimilhança obtida baseada nas \(1000\) simulações realizadas. Note que tal média é também uma estimativa para a esperança de \(\hat{\theta}\) que sabemos neste caso ser assintóticamente \(\theta\). É também evidente que com uma amostra maior a variância do EMV vai diminuindo, até no caso limite quando \(n \to \infty\) a variância converge para \(0\) mostrando a consistência do EMV. Em termos gráficos a distribuição deve se tornar uma distribuição degenerada no ponto \(\theta\). É interessante observar que mesmo com uma amostra pequena, os resultados válidos assintoticamente já apresentam resultados excelentes. É claro que este é um exemplo simples, porém como veremos na sequência deste livro mesmo em modelos mais complexos, como nos modelos lineares generalizados (MLG) estes resultados permanecem igualmente bons.
2.7 Intervalos de confiança
Como vimos no Capítulo 2 há pelo menos três formas básicas para obtenção de intervalos de confiança baseados na função de verossimilhança. A intuitivamente mais simples é baseada na verossimilhança relativa, isto é, o intervalo é definido pelo conjunto de valores do parâmetro que tenham uma verossimilhança não inferior a um certo percentual da verossimilhança máxima. O intervalo obtido desta forma não tem interpretações probabilísticas. A segunda forma baseia-se na função deviance. Considerando a sua distribuição assintótica (ver Teorema 2.5), define-se um ponto de corte nesta função e o intervalo é dado pelo conjunto dos valores para o parâmetro que possuem deviance inferior a esse valor. A terceira utiliza uma aproximação quadrática da superfície de log-verossimilhança. As últimas duas opções associam uma interpretação frequentista ao intervalo de confiança. Desta forma, os objetivos deste exemplo são: mostrar como obter os intervalos de confiança por cada uma das três abordagens, explorar as relações existentes e discutir algumas possíveis dificuldades computacionais que podem ocorrer quando trabalhamos diretamente com a função deviance.
Considere o caso onde amostras independentes de uma variável aleatória \(Y_i\) com \(i = 1,\ldots,n\) cada uma com distribuição exponencial de parâmetro \(\theta\) esteja disponível, vamos denotar isto por, \(Y_i \sim \mathrm{Exp}(\theta)\). O objetivo é estimar o parâmetro \(\theta\) e fornecer um ou mais intervalos de confiança, digamos \(\hat{\theta}_L\) e \(\hat{\theta}_U\) para \(\theta\). Se adotarmos, um enfoque frequentista o intervalo terá probabilidade \(1 - \alpha\) de conter \(\theta\). Note que a estrutura probabilística está em \(\hat{\theta}_L\) e \(\hat{\theta}_U\).
O primeiro passo é sempre escrever a função de verossimilhança, \[ \mathrm{L}(\theta) = \prod_{i=1}^n \theta \exp\{-\theta y_i\} = \theta^n \exp\{-\theta \sum_{i=1}^n y_i\} = \theta^n \exp\{-n \overline{y} \theta \}. \]
Consequentemente, a função de log-verossimilhança é \[ \mathrm{l}(\theta) = n \log \theta - \theta \sum_{i=1}^n y_i = n \log \theta - \theta n \overline{y}. \] Derivando a log-verossimilhança em \(\theta\) chegamos a função escore
\[ U(\theta) = n \theta^{-1} - n \overline{y}. \]
Para encontrar a estimativa de máxima verossimilhança basta igualar a função escore a \(0\) e isolar o \(\theta\) isto resulta
\[ \hat{\theta} = \frac{1}{\overline{y}}. \]
A segunda derivada da função de log-verossimilhança tem um papel fundamental na construção de intervalos de confiança por aproximação quadrática da função de verossimilhança, uma vez que ela mede a curvatura da função no entorno do ponto de máximo. Em termos estatísticos, trabalhamos com a informação observada ou esperada, uma vez que esta quantidade descreve o comportamento assintótico dos estimadores de máxima verossimilhança, já que sua inversa fornece a variância do estimador. Neste caso a função de log-verossimilhança é côncava e polinomial de ordem infinita. As informações esperada e observada são iguais e dependem do valor do parâmetro e na prática é necessário usar a informação estimada pela amostra. \[ I_O(\theta) = I_E(\theta) = n \theta^{-2} \;\; \mbox{ e } \;\; I_O(\hat{\theta}) = I_E(\hat{\theta}) = n \hat{\theta}^{-2}. \]
Para encontrar o intervalo de confiança vamos começar pela função deviance, lembrando que de acordo com o Teorema 2.5, a deviance segue uma distribuição \(\chi^2\) com \(d\) graus de liberdade, no exemplo \(d = 1\). Desta forma o valor de \(c^*\) é obtido definindo algum quantil \(q_{1-\alpha}\) da distribuição qui-quadrado com \(1\) grau de liberdade e \(1-\alpha\) de confiança. Como exemplo, fixando \(\alpha = 0,05\) toma-se o valor do quantil \(c^* = 3,84\). Com isto, temos os elementos necessários para construir o intervalo de confiança baseado na função deviance que é dado pelo conjunto de valores que obedecem:
\[\begin{eqnarray} \mathrm{D}(\theta) &=& 2 [ \mathrm{l}(\hat{\theta}) - \mathrm{l}(\theta)] \nonumber \\ &=& 2 [ n \log \hat{\theta} - \hat{\theta} n \overline{y} - ( n \log \theta - \theta n \overline{y}) ] \nonumber \\ &=& 2n [ \log \left(\hat{\theta}/\theta \right) + \overline{y} ( \theta - \hat{\theta}) ] \leq c^* \tag{2.3} \end{eqnarray}\]
Os limites \((\hat{\theta}_L, \hat{\theta}_U)\) são encontrados resolvendo a equação em (2.3), mas mesmo em uma situação simples como a deste exemplo a obtenção das raízes requer a solução de uma equação não-linear que não tem solução analítica. Desta forma, algum método numérico é necessário para encontrar os limites do intervalo.
Uma outra opção para encontrar o intervalo de confiança é fazer uma aproximação quadrática utilizando séries de Taylor para a função \(\mathrm{l}(\theta)\) em torno do ponto \(\hat{\theta}\) e usar esta aproximação no lugar da função de log-verossimilhança original. Neste caso, os limites do intervalo são as raízes de um polinômio de segundo grau e os intervalos são da forma \[ \hat{\theta} \pm z_{\frac{\alpha}{2}} \sqrt{ V(\hat{\theta})} , \] o que corresponde a usar o resultado do Teorema 2.4.
Para a distribuição exponencial, temos que a \(\mathrm{V}(\hat{\theta}) = \mathrm{I_O}^{-1}(\hat{\theta}) = \hat{\theta}^2/n\), logo o intervalo de confiança é dado por \[\hat{\theta}_L = \hat{\theta} - z_{\frac{\alpha}{2}} \hat{\theta}/\sqrt{n} \quad \text{e} \quad \hat{\theta}_U = \hat{\theta} + z_{\frac{\alpha}{2}} \hat{\theta}/\sqrt{n} . \]
Aqui a construção do intervalo de confiança fica bastante facilitada. Conhecendo o valor de \(z_{\frac{\alpha}{2}}\) o intervalo se resume a uma conta simples, ou seja, não é necessário utilizar métodos numéricos para obtenção dos limites do intervalo. Como a distribuição amostral de \(\hat{\theta}\) é assintoticamente gaussiana podemos escolher o valor de \(z_{\frac{\alpha}{2}}\) como o quantil da distribuição normal, com \((1-\alpha)\) 100% de confiança, escolhendo \(\alpha = 0,05\), temos aproximadamente que \(z_{\frac{\alpha}{2}} = 1,96\). No caso de \(d=1\) o quantil da distribuição \(\chi^2_{(1)}\) é o quadrado de um score \(z\) da distribuição normal e o método também corresponde a obter o intervalo como na função deviance porém utilizando a sua aproximação quadrática dada por: \[ \mathrm{D}(\theta) \approx n \left(\frac{\theta-\hat{\theta}}{\hat{\theta}} \right)^2. \] Desta forma as raízes que definem os limites dos intervalos equivalentes aos anteriores são: \[ \left(\hat{\theta}_L \approx \hat{\theta} (1-\sqrt{c^*/n}) \;\; , \;\; \hat{\theta}_U \approx \hat{\theta} (1+\sqrt{c^*/n})\right) . \]
A última opção que vamos considerar é a construção do intervalo definindo um valor limite para a verossimilhança relativa. Um intervalo baseado em verossimilhança relativa é da forma \(LR(\theta) = \frac{L(\theta)}{L(\hat{\theta})} \ge r\), onde \(r\) representa um percentual do máximo da função de verossimilhança, para o qual admite-se ainda obter uma estimativa aceitável de \(\theta\). Por exemplo, definindo \(r=0.25\), o intervalo é definido pelo valores que apresentam uma verosimilhança que seja ao menos 25% da máxima para o conjunto de dados. Para escolher um valor de \(r\) comparável com o escolhido para a deviance, note o seguinte: \[\begin{eqnarray*} \frac{L(\theta)}{L(\hat{\theta})} &\ge& r \\ \log \left[ \frac{L(\theta)}{L(\hat{\theta})} \right] &\ge& \log r \\ -2[ l(\theta) - l(\hat{\theta})] &\ge& 2 \cdot \log r\\ -3,84 & \ge& 2 \cdot \log r \\ r &\approx& 0,146 \end{eqnarray*}\]
A Tabela 2.1 mostra a relação entre alguns valores de corte da verossimilhança relativa e os valores correspondentes em log-verossimilhança e em deviance. Na prática, os níveis de confiança são aproximados e válidos apenas assintóticamente.
| r | c | c. | Prob |
|---|---|---|---|
| 50% | 0.693 | 1.39 | 0.761 |
| 26% | 1.347 | 2.69 | 0.899 |
| 15% | 1.897 | 3.79 | 0.949 |
| 3.6% | 3.324 | 6.65 | 0.990 |
Com isso, podemos observar que usar a verossimilhança relativa ou a deviance são formas equivalentes de construir o intervalo de confiança. A diferença está na interpretação que é associada aos intervalos. Uma discussão aprofundada pode ser encontrada em Royall (1997). A vantagem em usar a deviance é que conhecemos a sua distribuição assintótica o que permite a construção de intervalos de confiança com interpretação probabilística. Da mesma forma que para a deviance, no exemplo, a obtenção do intervalo pela verossimilhança relativa também requer resolver um sistema não-linear utilizando algum método numérico para encontrar as raízes da equação \(\mathrm{LR}(\theta) \ge r\).
Considere dados gerados do modelo exponencial com os comando abaixo.
set.seed(123) ; y <- rexp(20, rate=1)Vamos implementar as funções de verossimilhança, log-verossimilhança, deviance e deviance aproximada para termos uma visualização gráfica da relação entre as diferentes estratégias para construir o intervalo de confiança.
grid.theta <- seq(0.68,2,l=100)
# Verosssimilhança
Lik <- function(theta,y){
Lt <- prod(dexp(y,rate=theta,log=FALSE))
return(Lt)
}
L.theta <- sapply(grid.theta, Lik, y=y)
LR.theta <- L.theta/Lik(theta=1/mean(y),y=y)
# log-verossimilhança
ll <- function(theta,y){
llt <- sum(dexp(y,rate=theta,log=TRUE))
return(llt)
}
ll.theta <- sapply(grid.theta, ll, y=y)
# Deviance
dev.theta <- 2*(ll(1/mean(y),y=y)-ll.theta)
# Deviance aproximada
dev.aprox <- function(theta,theta.hat,y){
dev <- (theta - theta.hat)^2*(length(y)/(theta.hat^2))
return(dev)
}
devA.theta <- sapply(grid.theta, dev.aprox, theta.hat = 1/mean(y), y=y)Figura 2.4 apresenta os gráficos com os pontos de corte indicados de forma equivalente em todas as funções.
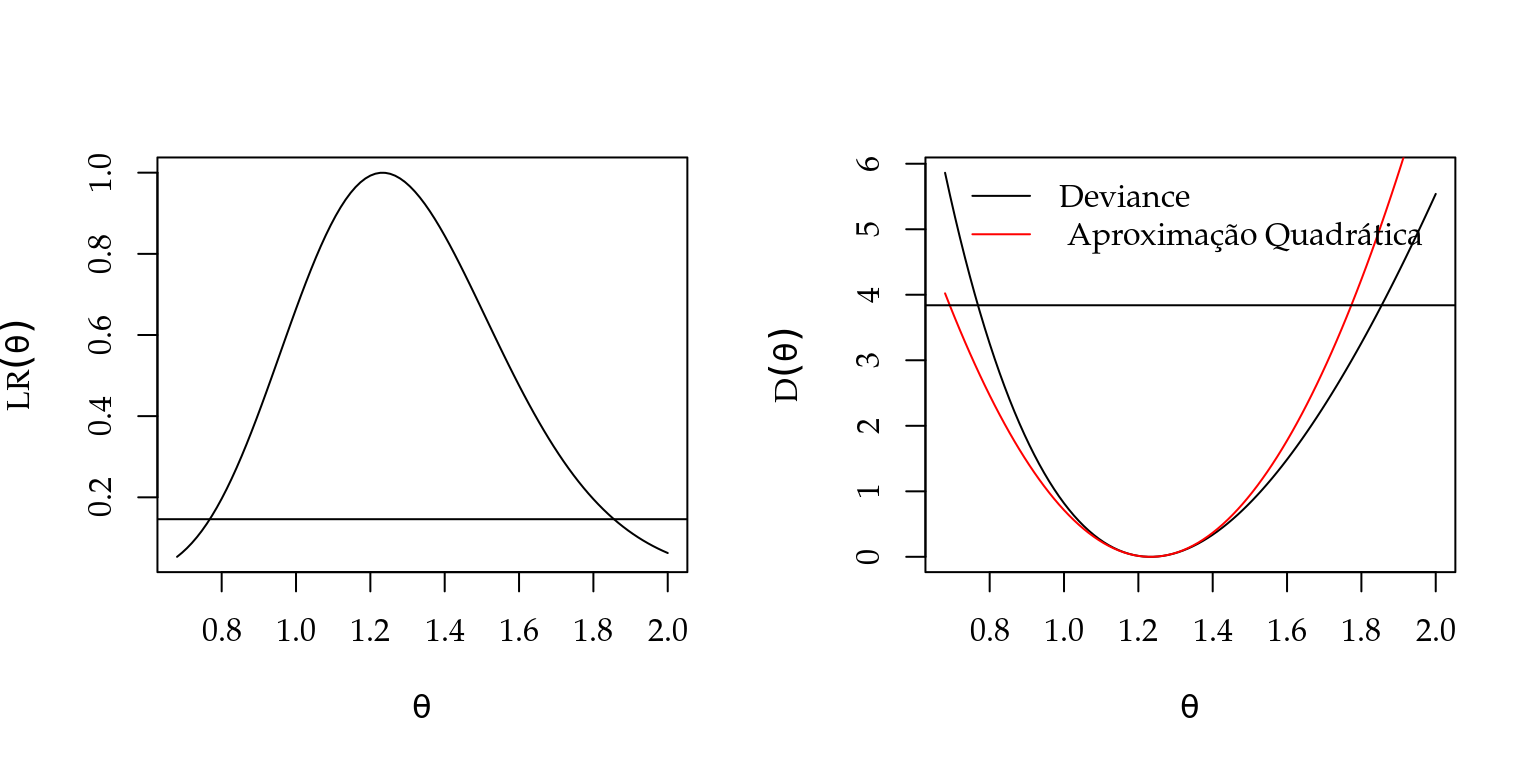
Figura 2.4: Verossimilhança relativa (esquerda) e função deviance exata e aproximada (direita) - Distribuição exponencial.
A estimativa de máxima verossimilhança para a amostra simulada.
theta.est <- round(1/mean(y), dig=2)
theta.est## [1] 1.23Como é possível ver na Figura 2.4 a função deviance é razoavelmente aproximada por uma forma quadrática mas esta aproximação vai depender do valor do parâmetro e do tamanho da amostra. Para obter os limites inferior e superior do intervalo de confiança pela aproximação quadrática temos: \[ \hat{\theta}_L = \hat{\theta} - z_{\frac{\alpha}{2}} \sqrt{\hat{\theta}^2/n} \quad \text{e} \quad \hat{\theta}_U = \hat{\theta} + z_{\frac{\alpha}{2}} \sqrt{\hat{\theta}^2/n} \]
Para a amostra simulada utilizada para gerar os gráficos temos os seguintes valores:
Ic_min <- theta.est - 1.96*sqrt( (theta.est^2)/20 )
Ic_max <- theta.est + 1.96*sqrt( (theta.est^2)/20 )
c(Ic_min, Ic_max)## [1] 0.691 1.769Usando a função deviance precisamos resolver uma equação não-linear.
Novamente temos diversas opções para resolver tal equação em R. Poderíamos usar os métodos gradiente descendente ou Newton-Raphson que implementamos anteriormente.
Porém, é mais fácil usar as funções do pacote rootSolve (Soetaert 2009).
O primeiro passo é escrever a função deviance,
ICdevExp <- function(theta, theta.hat, y, nivel = 0.95){
n <- length(y)
dv <- 2*n*( log( theta.hat/theta) + mean(y)*(theta- theta.hat))
return(dv - qchisq(nivel,df=1))
}Uma vez com a função escrita podemos encontrar suas raízes usando a função uniroot.all().
require(rootSolve)
uniroot.all(ICdevExp, interval = c(0,10), theta.hat = 1/mean(y), y = y)## [1] 0.768 1.855A Figura 2.4 mostra o intervalo aproximado pela forma quadrática com um deslocamento para a esquerda quando comparado com o intervalo baseado na função deviance. É importante ter bastante cuidado na interpretação destes intervalos. De acordo com a interpretação frequentista de probabilidade, se realizarmos o mesmo experimento um grande número de vezes e em cada um destes experimentos calcularmos o respectivo intervalo de confiança esperamos que \((1-\alpha)\) 100% dos intervalos construídos contenham o verdadeiro valor do parâmetro. Vamos ilustrar esta interpretação através de um estudo de simulação. Para isto, vamos gerar 100 amostras do modelo exponencial com \(\theta = 1\), sendo cada amostra de tamanho \(n = 70\). Para cada amostra vamos obter o intervalo de confiança baseado na função deviance e vamos verificar o percentual de intervalos que contêm o verdadeiro valor do parâmetro.
THETA <- 1
set.seed(12)
ic <- matrix(NA, ncol=2, nrow=100)
for(i in 1:100){
y <- rexp(70, rate=THETA)
est <- 1/mean(y)
ic[i,] <- uniroot.all(ICdevExp, int=c(0,5), theta.hat=est, y=y)
}
mean(apply(ic, 1, function(x) (x[1] < THETA & x[2] > THETA)))## [1] 0.95No código acima simulamos a cada passo do laço for() uma nova realização da variável aleatória \(Y\), com esta realização calculamos a estimativa de máxima verossimilhança e o seu respectivo intervalo de confiança baseado na deviance e guardamos o resultado em um objeto chamado \(ic\). De acordo com a interpretação frequentista dos \(100\) intervalos de confiança que calculamos esperamos que \(95\) deles contenham o verdadeiro valor do parâmetro neste caso \(\theta = 1\). O gráfico apresentado na Figura 2.5 ilustra os resultados. Neste caso, conforme esperado, temos exatamente que \(5\) dos intervalos não contem o valor verdadeiro do parâmetro. É claro que por se tratar de um exemplo de simulação variações podem ocorrer.
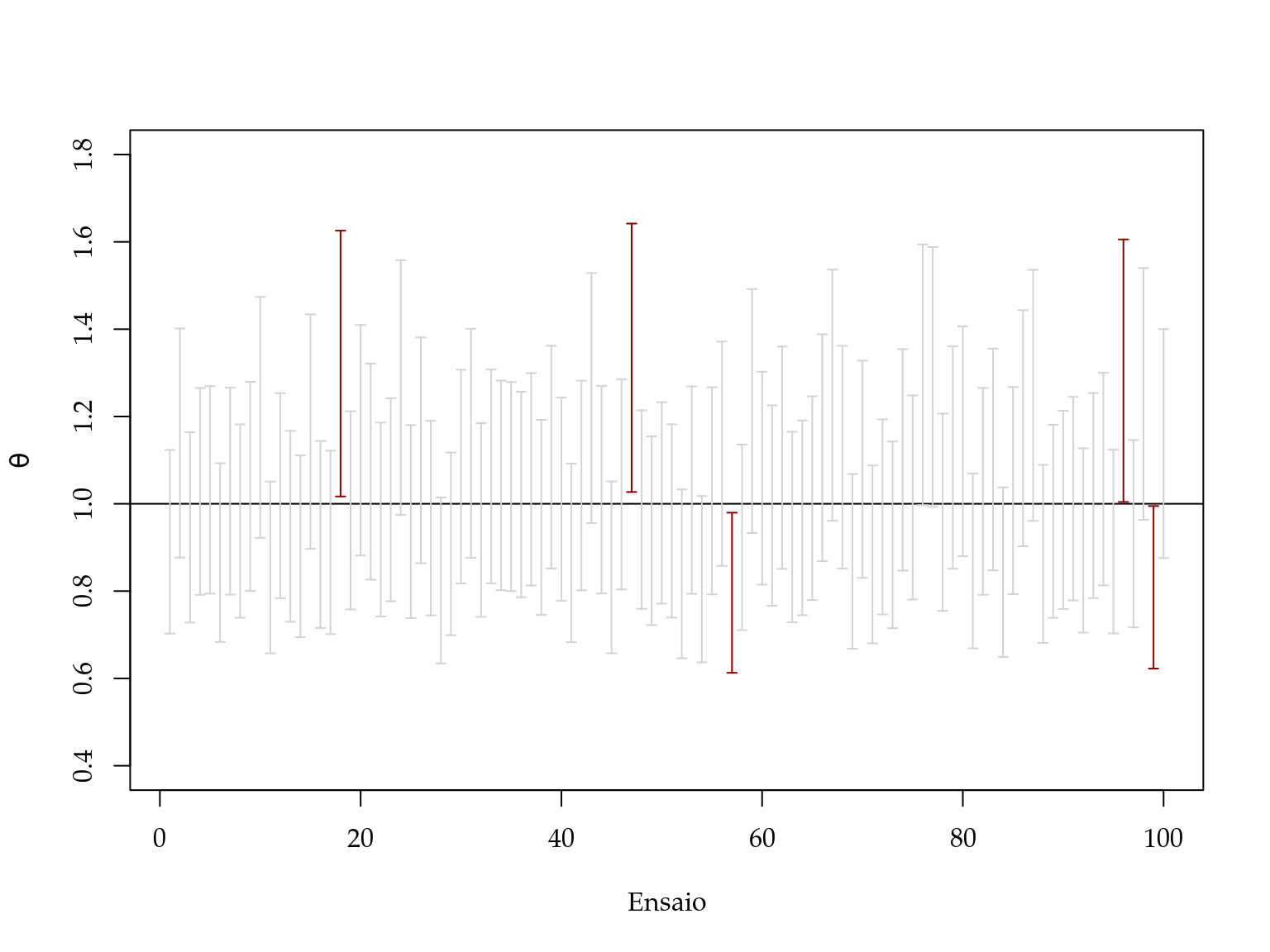
Figura 2.5: Ilustração da interpretação frequentista de intervalo de confiança.
A taxa de cobertura de um intervalo é a proporção de vezes em que os intervalos contêm o verdadeiro valor do parâmetro sobre o total de ensaios simulados. Neste caso obtivemos exatamente \(95/100\), ou seja, a taxa de cobertura é de \(95\)% igual ao nível nominal especificado. A taxa de cobertura é uma forma muito utilizada para avaliar e comparar métodos de construção de intervalos de confiança. Em modelos mais complexos principalmente os que envolvem efeitos aleatórios, os componentes de variância são de difícil estimação e os seus intervalos de confiança principalmente os construídos baseados em aproximação quadrática da log-verossimilhança apresentam taxa de cobertura abaixo do nível nominal especificado.
Para ilustração desta ideia vamos refazer nosso estudo de simulação, porém desta vez vamos usar o intervalo de confiança baseado na aproximação quadrática da deviance que é de fácil obtenção.
THETA <- 1
set.seed(12)
ic <- matrix(NA, ncol=2, nrow=100)
for(i in 1:100){
y <- rexp(70, rate=THETA)
est <- 1/mean(y)
erro <- 1.96*sqrt( (est^2)/70)
ic[i,] <- c(est - erro, est + erro)
}
mean(apply(ic, 1, function(x) (x[1] < THETA & x[2] > THETA)))## [1] 0.96Vamos mostrar os intervalos obtidos e verificar quais contêm o verdadeiro valor do parâmetro. Os resultados não apresentados na Figura 2.6.
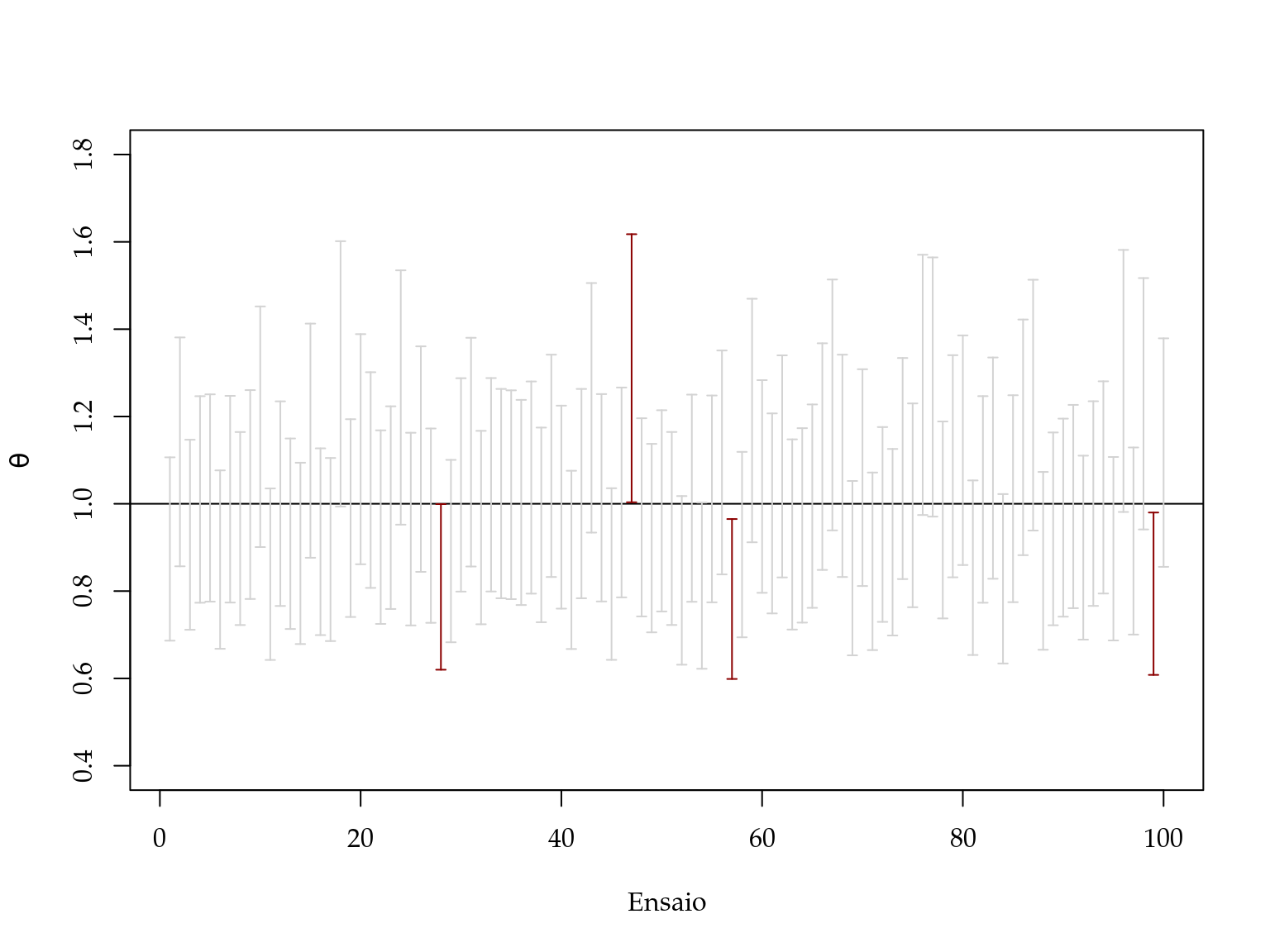
Figura 2.6: Ilustração da interpretação frequentista de intervalo de confiança.
Neste caso, temos que apenas \(4\) dos \(100\) intervalos de confiança obtidas continham o verdadeiro valor do parâmetro, o que leva a uma taxa de cobertura de \(96\%\) ligeiramente acima do nível especificado. Este foi apenas um simples exemplo e convidamos o leitor interessado a fazer uma comparação mais profunda da taxa de cobertura destes intervalos para diferentes tamanhos de amostras e valores do parâmetro \(\theta\).
Para encerrar este exemplo vamos redefinir a função para obtenção do intervalo de confiança a partir da função deviance. Com isto pretendemos chamar a atenção para cuidados em não efetuar cálculos desnecessários nos códigos. Na função original
n <- length(y) e mean(y) são avaliados a cada chamada da função. Entretanto, para uma determinada amostra, estas quantidades são constantes. Em procedimentos numéricos a função é avaliada muitas vezes e portanto estas constantes são recalculadas desnecessariamente a cada avaliação. É melhor então definir a função já recebendo estas constantes que são estatísticas suficientes que resumem a amostra.
Usamos ainda o fato que \(\hat{\theta} = 1/\overline{y}\).
ICdevExp <- function(theta, amostra, nivel=0.95){
## amostra é um vetor com elementos n e mean(y), nesta ordem
n <- amostra[1]
med <- amostra[2]
dv <- 2*n*(-log(med*theta) + med*theta - 1)
return(dv - qchisq(nivel, df=1))
}
am <- c(length(y), mean(y))
uniroot.all(ICdevExp, interval=c(0,10), amostra=am)## [1] 0.876 1.4002.8 Testes de hipótese
Em situações práticas podemos estar interessados em testar se o parâmetro de um dado modelo é igual, maior ou menor que algum valor de interesse. Conforme descrito no Capítulo 2, um teste de hipótese é qualquer afirmação acerca da distribuição de probabilidade de uma ou mais variáveis aleatórias. Considere a situação onde observamos uma amostra aleatória de tamanho \(n\) de uma população com distribuição Bernoulli de parâmetro \(\theta\). Suponha que o interesse é testar sob a hipótese nula \(H_0 : \theta = \theta_0\) contra uma hipótese alternativa \(H_1 : \theta \neq \theta_0\). Vimos na Seção 2.3 três formas de construir testes de hipótese que podem ser usadas para concluir sobre as hipóteses levantadas. Como exemplo didático, vamos obter as três estatísticas de teste para o caso onde \(Y_i \sim B(\theta)\).
Como as amostras são independentes a função de verossimilhança deste modelo é dada por, \[ \mathrm{L}(\theta) = \prod_{i=1}^n \theta^{y_i}(1-\theta)^{(1-y_i)} = \theta^{\sum_{i=1}^n y_i} (1-\theta)^{(n - \sum_{i=1}^n y_i)}. \]
A função de log-verossimilhança, \[ \mathrm{l}(\theta) = \sum_{i = 1}^n y_i \ln(\theta) + (n - \sum_{i=1}^n y_i) \ln(1-\theta). \]
A função escore é obtida derivando a log-verossimilhança em \(\theta\), \[ \mathrm{U}(\theta) = \frac{\sum_{i=1}^n y_i}{\theta} - \frac{n - \sum_{i=1}^n y_i}{(1-\theta)} = \frac{\sum_{i=1}^n y_i - n \theta}{\theta(1-\theta)}, \]
que sendo resolvida fornece a estimativa de máxima verossimilhança
\[ \hat{\theta} = \frac{\sum_{i=1}^n y_i }{n} = \overline{y}. \] Além disso, temos que a informação observada é dada por \[ \mathrm{I_O}(\theta) = +\frac{\sum_{i=1}^n y_i}{\theta^2} + \frac{(n-\sum_{i=1}^n y_i)}{(1-\theta)^2}. \] Para obter a informação esperada avaliamos a esperança da informação observada
\[ \mathrm{I_E}(\theta) = \mathrm{E}(\mathrm{I_O}(\theta)) = \frac{n}{\theta(1-\theta)}. \]
Vamos começar pelo teste de razão de verossimilhança. A estatística do teste de razão de verossimilhança neste caso toma a seguinte forma:
\[ \lambda(\mathbf{y}) = \frac{\mathrm{L}(\theta_0 | \mathbf{y})}{\mathrm{L}(\hat{\theta}| \mathbf{y})}, \] que é a verossimilhança relativa. Note que \(-2 \log \lambda(\mathbf{y})\) é exatamente a função deviance usada para construir intervalos de confiança. Então,
\[ -2\lambda(\mathbf{y}) = -2\left \{ \sum_{i=1}^n y_i \ln \left ( \frac{\theta_0}{\hat{\theta} } \right ) + (n - \sum_{i=1}^n y_i)\ln \left ( \frac{1-\theta_0}{1-\hat{\theta}} \right ) \right \}. \]
A hipótese nula \(H_0 : \theta = \theta_0\) será rejeitada se, e somente se, \(-2 \log \lambda(\mathbf{y}) \ge \chi_{1,\alpha}^2\). A probabilidade de Erro do Tipo I será aproximadamente \(\alpha\).
O segundo método para construção de testes de hipóteses é o método de Wald. Se \(\hat{\theta}\) é o estimador de máxima verossimilhança a estatística do teste de Wald é dada por \[ T_w = \frac{\hat{\theta} - \theta_0}{\sqrt{ \mathrm{V}(\hat{\theta})}} \sim N(0,1). \] Sabemos que \(\mathrm{V}(\hat{\theta}) = \mathrm{I_E}^{-1}(\hat{\theta})\), então \(\mathrm{V}(\hat{\theta}) = \frac{\hat{\theta}(1 - \hat{\theta})}{n}\). Logo o teste de Wald no caso Bernoulli resume-se a \[ T_w = \frac{\hat{\theta} - \theta_0}{ \sqrt{\frac{\hat{\theta}(1 - \hat{\theta})}{n} }} \sim N(0,1). \] Dado a distribuição assintótica do teste para encontrar a região de rejeição basta encontrar o quantil da distribuição gaussiana padrão correspondente ao nível de confiança desejado.
A terceira opção é a estatística de teste que é dada por, \[ T_E = \frac{\mathrm{U}(\theta_0)}{\sqrt{\mathrm{I_E}(\theta_0)}} . \] Substituindo as quantidades previamente encontradas temos para o caso Bernoulli, \[ T_E = \frac{\sum_{i=1}^n y_i - n \theta}{\theta(1-\theta)} \sqrt{\frac{\theta(1-\theta)}{n}} = \frac{\sum_{i=1}^n y_i - n \theta}{\sqrt{n\theta(1-\theta)}} \sim N(0,1) . \]
A Figura 2.7 ilustra a construção dos testes de hipóteses e os relaciona à função de verossimilhança do modelo. O teste da razão de verossimilhança compara valores no eixo vertical, ou seja, compatibilidades com os dados. O teste escore avalia o quanto a curvatura da função no ponto especificado pelo teste se afasta de zero, o valor no máximo. O teste de Wald avalia a distância entre o valor especificado no teste e o EMV, padronizando esta distância pela curvatura da função ao redor de seu máximo.
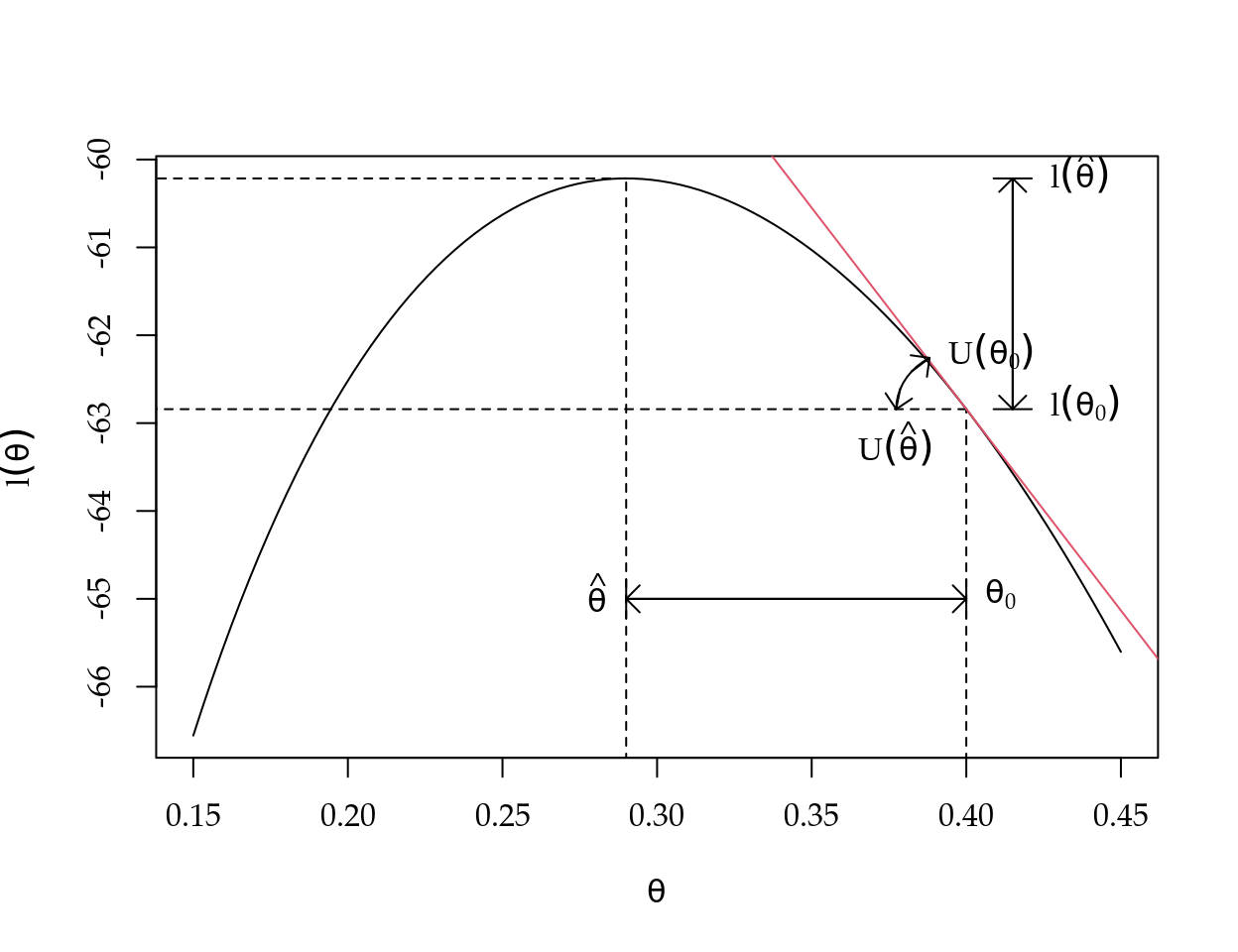
Figura 2.7: Diferentes formas de construir teste de hipótese baseado em verossimilhança - Distribuição Bernoulli
Para exemplificar a execução do teste de hipóteses vamos utilizar um conjunto de dados simulados com \(n = 100\) amostras aleatórias de uma Bernoulli com \(\theta = 0.3\). Vamos supor que o interesse seja testar sob \(H_0: \theta = 0.4\) contra \(H_1 : \theta \neq 0.4\). As funções abaixo montam a estrutura do teste de hipótese de acordo com cada abordagem.
trv <- function(Est, H0, alpha, ...) {
critico <- qchisq(1-alpha, df=1)
est.calc <- Est(H0, ...)
print(ifelse(est.calc < critico, "Aceita H0", "Rejeita H0"))
return(c(est.calc,critico))
}wald <- function(H0, EMV, V.EMV, alpha){
critico <- qnorm(1-alpha/2)
Tw <- (EMV - H0)/sqrt(V.EMV)
print(ifelse(abs(Tw) < critico, "Aceita H0", "Rejeita H0"))
return(c(Tw,critico))
}escore <- function(H0, U, Ie, alpha, ...){
critico <- qnorm(1-alpha/2)
Te <- U(H0,...)/sqrt(Ie(H0,...))
print(ifelse(abs(Te) < critico, "Aceita H0", "Rejeita H0"))
return(c(Te,critico))
}A seguir usamos as funções para efetuar os testes baseado em uma amostra simulada do modelo Bernoulli.
set.seed(123)
dados <- rbinom(100, prob = 0.3, size = 1)
## Estatistica do TRV caso Bernoulli
Est <- function(H0, y){
theta.hat <- mean(y)
n <- length(y)
lv <- -2*(sum(y)*log(H0/theta.hat) + (n - sum(y))*log( (1-H0)/(1-theta.hat) ) )
return(lv)
}
## Procedendo com o TRV theta0 = 0.4
trv(Est = Est, H0 = 0.4, alpha = 0.05, y = dados)## [1] "Rejeita H0"## [1] 5.25 3.84## Teste de Wald
V.EMV <- mean(dados)*(1-mean(dados))/length(dados)
wald(H0 = 0.4, EMV = mean(dados), V.EMV = V.EMV, alpha = 0.05)## [1] "Rejeita H0"## [1] -2.42 1.96O teste escore é ligeiramente mais complicado uma vez que é necessário programar a função escore e a informação esperada.
U <- function(theta, y) {
n <- length(y)
esco <- (sum(y)/theta) - ((n-sum(y))/(1-theta))
return(esco)
}Ie <- function(theta, y) {
n <- length(y)
IE <- n/(theta*(1-theta))
return(IE)
}escore(H0 = 0.4, U = U, Ie = Ie, alpha = 0.05, y = dados)## [1] "Rejeita H0"## [1] -2.25 1.96Neste caso os três testes levam a mesma conclusão. Em geral, o teste escore é o que requer mais cálculos, uma vez que exige a obtenção da função escore e da informação esperada, o que em geral é feito analiticamente. Por outro lado, tem uma clara vantagem sobre os demais porque não exige a avaliação da função de log-verossimilhança e nem mesmo a obtenção da estimativa de máxima verossimilhança. O teste de Wald é o mais utilizado pelo menos de forma inicial uma vez que sua construção é simples. O teste da razão de verossimilhança é também muito utilizado, tanto para testar valores para um determinado parâmetro quanto para a comparação de modelos aninhados. Na situação em que usamos métodos numéricos para maximização da função de log-verossimilhança um subproduto é a informação observada que pode ser usada diretamente na estatística de teste de Wald. Além disso, quando comparamos modelos aninhados a diferença entre os valores da log-verossimilhança dos modelos, permite a construção do teste da razão de verossimilhança de forma bastante direta, porém requer duas otimizações, uma para cada modelo, enquanto que o de Wald apenas uma.
2.9 Reparametrização
Em diversas aplicações o interesse principal pode ser sobre alguma função de um parâmetro do modelo. Por exemplo em uma distribuição exponencial de parâmetro \(\theta\) o interesse pode estar na probabilidade de obter um valor maior que \(k\) expressa por \(\psi = \exp\{-\theta k\}\), o que pode ser visto como uma reparametrização. Além disto, por vezes pode ser mais simples estimar em uma certa parametrização do que em outra. Por exemplo, no caso de parâmetros de variância em geral é mais estável numericamente estimar a sua raiz ou o log da raiz. Note também que reparametrizações mudam as regiões de busca em algoritmos de maximização.
Por exemplo, para parâmetros de variância digamos \(\sigma^2\) tem como seu intervalo de busca o \(\Re^+\), enquanto que se ao invés de estimar \(\sigma^2\) estimarmos \(\phi = \log \sqrt{\sigma^2}\) o intervalo de busca será toda a reta real, o que em geral é mais conveniente quando trabalha-se com algoritmos de maximização numérica.
Como exemplo ilustrativo deste problema, seja \(Y_i : i = 1, \ldots,n\) variáveis aleatórias independentes com função densidade de probabilidade dada por:
\[ \mathrm{f}(y; \theta) = 2 \theta y \exp^{\{ -\theta y^2\}} \quad: \quad y \ge 0. \]
Considere que seja de interesse a reparametrização \(\theta = \frac{1}{\mu}\). Vamos primeiro fazer todo o processo de inferência considerando que queremos estimar o parâmetro \(\theta\). Na sequencia realizamos todo o processo considerando o parâmetro \(\mu\). Para finalizar mostramos como passar de uma reparametrização para outra, ou seja, como obter as estimativas tanto pontuais quanto intervalares para \(\mu\) a partir das estimativas de \(\theta\).
Começamos escrevendo a função de verossimilhança, \[ \mathrm{L}(\theta) = \prod_{i=1} ^n 2 \theta y_i \exp\{-\theta y_i^2\} = ( 2 \theta)^n \prod_{i=1}^n y_i \exp\left[-\theta \sum_{i=1} ^n y_i^2\right], \] logo a função de log-verossimilhança, \[ \mathrm{l}(\theta) = n \log 2 + n \log \theta + \sum_{i=1}^n \log y_i - \theta \sum_{i=1} ^n y_i ^2. \] Derivando em relação a \(\theta\) chegamos a função escore, \[ \mathrm{U}(\theta) = \frac{n}{\theta} - \sum_{i=1}^n y_i^2. \] Igualando a zero encontramos a estimativa de máxima verossimilhança, \[ \hat{\theta} = \frac{n}{\sum_{i=1}^n y_i ^2} . \] Para a construção do intervalo de confiança usando a aproximação quadrática precisamos da segunda derivada, da qual derivamos a informação observada e/ou esperada, neste caso temos, \[ \mathrm{I_O}(\theta) = - \frac{\partial^2 \mathrm{l}(\theta)}{\partial \theta^2} = \frac{n}{\theta^2}. \] Para obter a informação esperada basta obter a esperança da informação observada, \[ \mathrm{I_E}(\theta) = \mathrm{E}(\mathrm{I_O}(\theta)) = \mathrm{E} \left( \frac{n}{\theta^2} \right) = \frac{n}{\theta^2}. \]
Neste caso em particular \(\mathrm{I_O}(\theta) = \mathrm{I_E}(\theta)\) pois não dependem de \(\mathbf{y}\), porém em geral isso não é válido. Com as expressões anteriores podemos estimar o parâmetro \(\theta\) e encontrar um intervalo de confiança aproximado usando a aproximação quadrática. Para obter intervalos de confiança baseado na função deviance precisamos resolver a seguinte equação não-linear, \[ \mathrm{D}(\theta) = 2 \left[ n \log \left( \frac{\hat{\theta}}{\theta} \right) + (\theta - \hat{\theta})\sum_{i=1} ^n y_i^2 \right] \le c^* . \]
Isto pode ser resolvido usando algum método numérico conforme já discutido.
Por agora, vamos simplesmente usar a função uniroot.all(), que implementa o método de Brent para uma função qualquer. Com isso, temos todo o processo de inferência completo,
podemos estimar pontualmente, obter intervalo de confiança aproximado ou baseado na deviance. Testes de hipóteses também podem ser obtidos facilmente.
Mas não estamos interessados em \(\theta\), mas sim em \(\mu\). Podemos então reescrever a verossimilhança como função de \(\mu\). \[ \mathrm{L}(\mu) = \prod_{i=1} ^n 2 \mu^{-1} y_i \exp\left[-\frac{y_i^2}{\mu}\right] = (2 \mu^{-1})^n \exp\left[-\frac{1}{\mu}\sum_{i=1}^n y_i^2\right] \prod_{i=1}^{n} y_i. \]
A log-verossimilhança é dada por, \[ \mathrm{l}(\mu) = n \log 2 - n \log \mu - \mu^{-1} \sum_{i=1}^n y_i^2 + \sum_{i=1}^n \log y_i. \] Derivando em \(\mu\) obtemos a função escore, \[ \mathrm{U}(\mu) = -\frac{n}{\mu} + \mu^{-2} \sum_{i=1}^n y_i^2 . \] Igualando a zero chegamos a estimativa de máxima verossimilhança, \[ \hat{\mu} = \frac{\sum_{i=1}^n y_i^2}{n} . \] Para a informação observada tem-se
\[\begin{align*} \mathrm{I_O}(\mu) &= -\frac{\partial^2 \mathrm{l}(\mu)}{\partial \mu^2} = - \frac{\partial}{\partial \mu} \left[-\frac{n}{\mu} + \mu^{-2} \sum_{i=1}^n y_i^2 \right] \\ &= - n \mu^{-2} + 2 \mu^{-3} \sum_{i=1}^n y_i^2 . \end{align*}\]
Para obter a informação esperada precisamos tomar a esperança de \(\mathrm{I_O}(\mu)\), \[ \mathrm{I_E}(\mu) = \mathrm{E}( \mathrm{I_O}(\mu)) = \mathrm{E} \left( - n \mu^{-2} + 2 \mu^{-3} \sum_{i=1}^n y_i^2 \right). \]
Neste passo é necessário calcular a \(\mathrm{E}(Y_i^2)\) que é a solução da integral \(\mathrm{E}(Y_i^2) = \int_{0}^{\infty} Y_i^2 2 \mu^{-1} Y_i \exp\left[-\frac{Y_i^2}{\mu}\right] dY_i = \mu\) que neste caso é possível de ser obtida analiticamente. Substituindo na equação acima temos, \[ \mathrm{I_E}(\mu) = \mathrm{E}[ - n \mu^{-2} + 2 \mu^{-3} n \mu] = n \mu^{-2} . \]
Neste caso, a informação observada é diferente da esperada e isto afeta a construção do intervalo de confiança baseado na aproximação quadrática, uma vez que muda a estimativa de variância do estimador de máxima verossimilhança. As duas formas são equivalentes assintoticamente, porém na situação real temos apenas uma amostra finita. Na maioria das situações em modelagem estatística quando métodos numéricos são utilizados não temos a opção de escolher entre a informação observada e esperada, quando a segunda derivada é obtida numericamente estamos diretamente usando a informação observada. Podemos dizer que usar a informação observada é acreditar plenamente na amostra observada, enquanto que usar a informação esperada estamos emprestando mais informação do modelo. Pensamos na informação observada como uma medida de curvatura local, por outro lado a informação esperada é uma medida de curvatura global.
A construção de intervalos de confiança baseados diretamente na função deviance é feita resolvendo a seguinte equação não linear, \[ \mathrm{D}(\mu) = 2 \left[ n \log \left(\frac{\mu}{\hat{\mu}}\right) + ( \mu^{-1} - \hat{\mu}^{-1}) \sum_{i=1}^n y_i^2 \right] . \]
Para exemplificar considere que a seguinte amostra foi observada \(y_i = 0.19 ; 1.68 ; 2.81 ; 0.59; 1.18\). Vamos fazer um gráfico da verossimilhança em cada parametrização. Começamos escrevendo as funções em R.
# Verossimilhança para theta
L.theta <- function(theta, y){
n <- length(y)
return((2 * theta)^n * prod(y) * exp(-theta*sum(y^2)))
}
# Verossimilhança para mu
L.mu <- function(mu, y){
n <- length(y)
return((2*mu^-1)^n * prod(y) * exp( -(1/mu)*sum(y^2)))
}Vamos entrar com os dados no R em forma de vetor e calcular as estimativas de máxima verossimilhança para \(\theta\) e \(\mu\).
dados <- c(0.19,1.68,2.81,0.59,1.18)
theta.est <- length(dados)/sum(dados^2)
mu.est <- sum(dados^2)/length(dados)
c(theta.est, mu.est)## [1] 0.4 2.5Entretanto, na prática não é conveniente nem necessário reescrever a função de verossimilhança para cada reparametrização de interesse. Pela propriedade de invariância pode-se obter a função de verossimilhança de \(\mu\) partindo de \(\theta\) e vice-versa. Os gráficos da função de verossimilhança e log-verossimilhança nas duas parametrizações são apresentados na Figura 2.8.
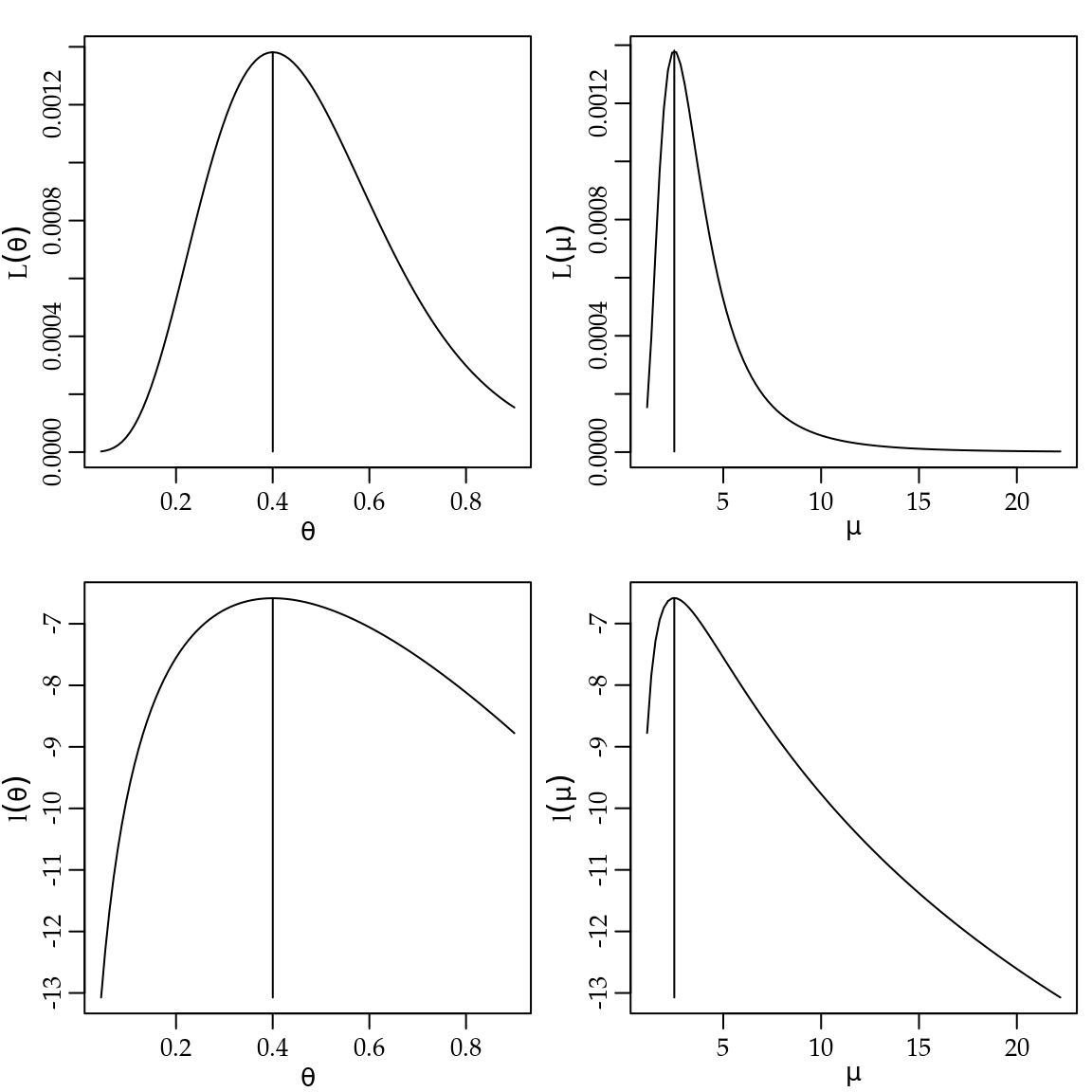
Figura 2.8: Verossimilhança e log-verossimilhança para theta e mu.
Para a construção dos intervalos de confiança baseados na deviance em cada parametrização basta resolver as respectivas equações não lineares. Além disso, podemos obter os intervalos de confiança aproximados usando a informação observada e/ou esperada, dependendo da situação. A Figura 2.9, apresenta as funções deviance exatas e aproximadas em cada parametrização. Para isto, precisamos criar cada uma das funções, para depois poder avalia-las.
dev.theta <- function(theta, theta.hat, y, desloca=0){
saida <- 2*(length(y)*log(theta.hat/theta) -
(theta.hat - theta)*sum(y^2))
return(saida - desloca)
}
dev.mu <- function(mu, mu.hat, y, desloca=0){
saida <- 2*(length(y)*log(mu/mu.hat) +
((1/mu)-mu.hat^-1)*sum(y^2))
return(saida - desloca)
}
dev.app.theta <- function(theta, theta.hat, y){
return((theta - theta.hat)^2 * (length(y)/theta.hat^2))
}
dev.app.mu.obs <- function(mu, mu.hat, y){
Io <- -((length(y)/mu.hat^2) - (2*sum(y^2)/mu.hat^3))
return((mu - mu.hat)^2 * Io)
}
dev.app.mu.esp <- function(mu, mu.hat, y){
Ie <- length(y)/(mu.hat^2)
return((mu - mu.hat)^2 *Ie)
}Como é possível ver na Figura 2.9 a função deviance apresenta um comportamento bastante assimétrico o que torna a aproximação quadrática ruim. Neste caso, o pequeno tamanho da amostra prejudica a aproximação quadrática.
De acordo com as propriedades assintóticas do estimador de máxima verossimilhança, sabemos que \(\hat{\theta} \sim N(\theta, \mathrm{I^{-1}_E}(\theta))\) e que podemos substituir \(\mathrm{I_E}(\theta)\) por \(\mathrm{I_E}(\hat{\theta})\), \(\mathrm{I_O}(\theta)\) ou \(\mathrm{I_O}(\hat{\theta})\). Como visto anteriormente neste exemplo a informação esperada e a observada coincidem para \(\theta\). Então o intervalo de Wald fica dado por: \[ \hat{\theta}_L = \hat{\theta} - z_{\frac{\alpha}{2}} \sqrt{ \hat{\theta}^2/n} \quad \text{e} \quad \hat{\theta}_U = \hat{\theta} + z_{\frac{\alpha}{2}} \sqrt{ \hat{\theta}^2/n} . \]
O mesmo argumento assintótico é usado para construir o intervalo para \(\mu\), porém aqui a informação esperada difere da observada. Temos que a informação esperada é dada por \(\mathrm{I_E}(\hat{\mu}) = \frac{n}{\hat{\mu}^2}\) enquanto que a informação observada é dada por \(\mathrm{I_O}(\hat{\mu}) = -\frac{n}{\hat{\mu}^2} + \frac{2 \sum_{i=1}^N y_i^2}{\hat{\mu}^3}\), e o intervalo é construído exatamente igual ao anterior.
Para os intervalos baseados diretamente na função deviance precisamos resolver as respectivas equações não lineares. Isto pode ser resolvido numericamente usando a função uniroot.all(). Vamos obter os intervalos de confiança e fazer uma comparação qualitativa em ambas as parametrizações. Para isto criamos uma função genérica que recebe a estimativa de máxima verossimilhança, a informação esperada ou observada e o nível de confiança do intervalo e retorna os seus limites inferior e superior.
ic.assintotico <- function(EMV, Io, alpha){
return(EMV + c(-1, 1) * qnorm(1-alpha/2)*sqrt(Io^(-1)))
}Usando a função criada obtemos os intervalos assintóticos para \(\theta\) e \(\mu\).
n <- length(dados)
ic.theta <- ic.assintotico(EMV = theta.est,
Io = (n / theta.est^2), alpha=0.05)
ic.mu.obs <- ic.assintotico(EMV = mu.est,
Io = -n/mu.est^2 + (2*sum(dados^2))/(mu.est^3), alpha=0.05)
ic.mu.esp <- ic.assintotico(EMV = mu.est, Io = n/mu.est^2, alpha=0.05)Vamos também criar uma função genérica à qual tem como seu argumento principal a função deviance do modelo.
ic.deviance <- function(dev,intervalo,...){
ic <- uniroot.all(dev, interval=intervalo, ...)
return(ic)
}Usamos a função criada para obter os intervalos de confiança,
ic.dev.theta <- ic.deviance(dev=dev.theta, intervalo=c(0,10),
theta.hat=theta.est, y=dados, desloca=qchisq(0.95, df=1))
ic.dev.mu <- ic.deviance(dev=dev.mu, intervalo=c(0,100),
mu.hat=mu.est, y=dados, desloca=qchisq(0.95, df=1))A seguir comparamos os intervalos obtidos e notamos que a discrepância entre intervalos pela deviance exata e aproximada é maior para \(\mu\). Isto é explicado pelo fato da verossimilhança de \(\mu\) ser mais assimétrica do que a de \(\theta\). Este comportamento pode ser visualizado na Figura 2.9. Em geral recomenda-se que a codificação da função de verossimilhança seja sempre feita na parametrização que fornece a função mais próxima de um comportamento quadrático e isto é especialmente relevante se intervalos aproximados (assintóticos) vão ser utilizados.
rbind(ic.theta, ic.dev.theta)## [,1] [,2]
## ic.theta 0.0494 0.751
## ic.dev.theta 0.1436 0.860rbind(ic.dev.mu, ic.mu.obs,ic.mu.esp)## [,1] [,2]
## ic.dev.mu 1.163 6.97
## ic.mu.obs 0.309 4.69
## ic.mu.esp 0.309 4.69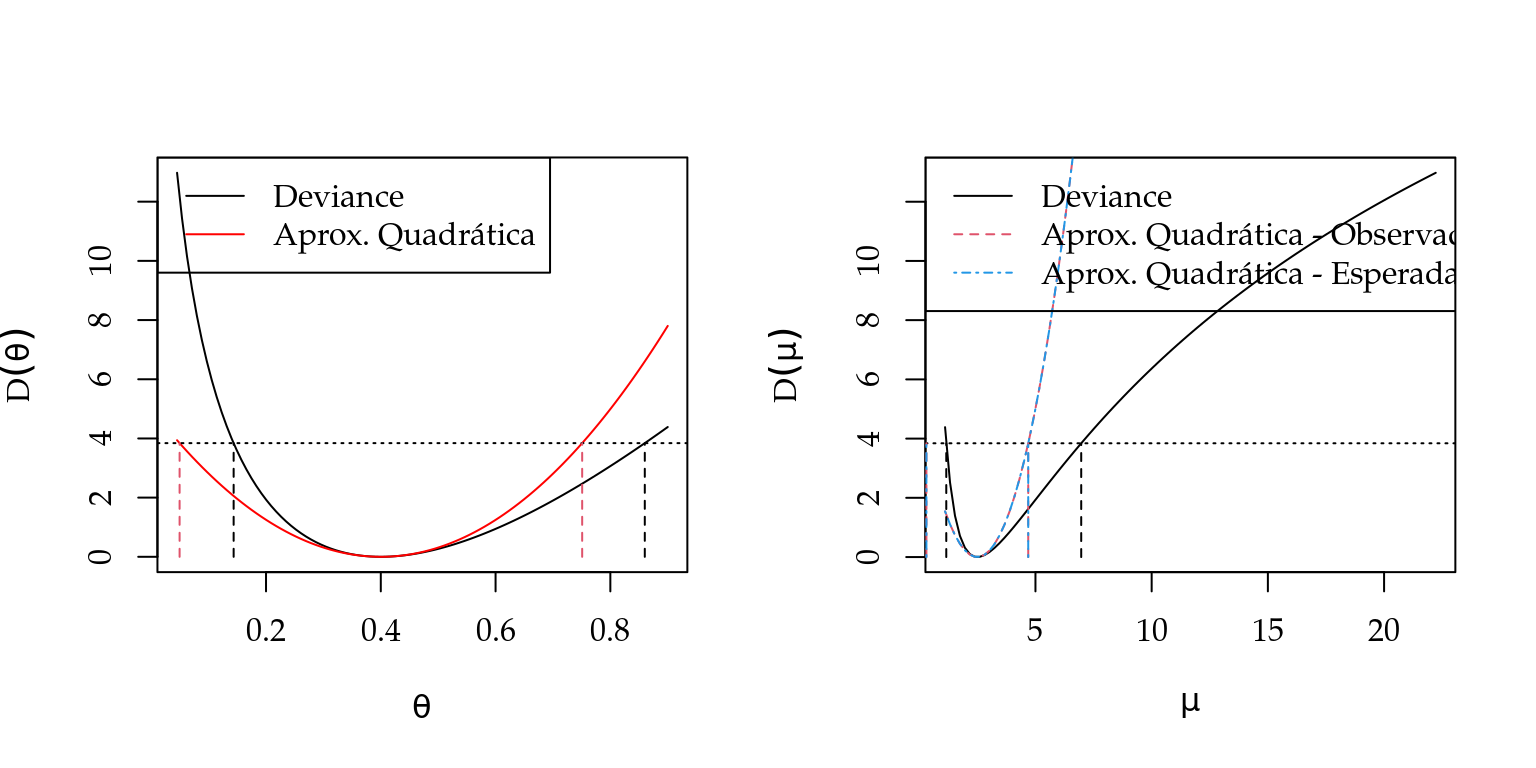
Figura 2.9: Deviances exatas e aproximadas para cada parametrização. Linhas verticais indicam os respectivos intervalos de confiança.
Em situações práticas não é necessário percorrer todo o caminho feito neste exemplo, que desenvolvemos aqui de forma completa para ilustrar e reforçar conceitos, já que, reparametrização é muito comum quando ajusta-se modelos mais complexos.
Considere que temos apenas as estimativas pontuais e intervalares de \(\theta\) e desejamos obter as estimativas pontual e intervalar para \(\mu\). Temos que $ = 1/$, logo \(\mu = 1/\theta\) por invariância \(\hat{\mu} = 1/\hat{\theta}\). Os intervalos obtidos diretamente baseado na função deviance também são invariantes então basta aplicar a transformação inversa igual feito para a estimativa pontual. Quando usamos a aproximação quadrática os intervalos não são invariantes, é neste ponto que usamos o Teorema 2.6. No exemplo, obtemos o intervalo aproximado para \(\theta\) usando por exemplo a informação esperada e desejamos o intervalo para \(\mu\). Usando o Teorema 2.6 sabemos que \(\mu = \mathrm{g}(\theta)\) e conhecemos a \(\mathrm{V}(\hat{\theta}) = \hat{\theta}^2 /n\), partindo disto precisamos encontrar a variância para \(\hat{\mu}\), o Teorema 2.6 diz que \(\mathrm{V}(\hat{\mu}) = g'(\hat{\theta})^2 I_E(\hat{\theta})^{-1}\), onde $ ^{}()$ representa a primeira derivada da função \(\mathrm{g}(\cdot)\). Sendo assim,
\[ \hat{\mu} = \frac{1}{\hat{\theta}} = \mathrm{g}(\hat{\theta}) \to \mathrm{g}^{\prime}(\hat{\theta}) = -\frac{1}{\hat{\theta}^2}. \] Logo, temos que
\[\begin{align*} \mathrm{V}(\hat{\mu}) &= \left( - \frac{1}{\hat{\theta}^2} \right)^2 \frac{ \hat{\theta}^2}{n} \\ &= \frac{1}{\hat{\theta}^4} \frac{\hat{\theta}^2}{n} = \frac{1}{\hat{\theta}^2 n} \\ &= \frac{1}{0.400^2 \cdot 10} = 0.625 \end{align*}\]
Fazendo as contas no R,
V.mu <- 1/(theta.est^2 * n)
ic.mu.theta <- c(1/theta.est - qnorm(0.975)*sqrt(V.mu),
1/theta.est + qnorm(0.975)*sqrt(V.mu))Comparando com o intervalo obtido anteriormente,
cbind(ic.mu.theta, ic.mu.esp)## ic.mu.theta ic.mu.esp
## [1,] 0.309 0.309
## [2,] 4.689 4.689Os intervalos são idênticos porém com um esforço de obtenção muito menor do que redefinir a verossimilhança. O Teorema 2.6 as vezes é chamado de método delta para obter variância de estimadores. Estes resultados dos estimadores de máxima verossimilhança são muito utilizados quando estamos programando modelos mais complexos, principalmente modelos com efeitos aleatórios, onde diversos parâmetros de variância/precisão serão estimados.
De forma geral, estes tipos de estimadores vão apresentar na parametrização original, uma distribuição amostral bastante assimétrica, além de problemas de representação numérica, tornando o uso de algoritmos numéricos difícil. Reparametrizações em termos de raízes e logaritmo são muito utilizadas para estabilizar os algoritmos numéricos e tornar a distribuição amostral dos estimadores mais próxima da gaussiana, o que também ajuda para a construção de intervalos baseados na aproximação quadrática. No caso de intervalos baseados na função deviance (exata), pela invariância a transformação de uma parametrização para outra é feita diretamente aplicando-se a transformação nos limites do intervalo. Para o caso da aproximação quadrática, a volta para a parametrização original pode ser feita pelo método delta. Desta forma é possível manter as interpretações desejadas em termos dos parâmetros de interesse do modelo e estimar na parametrização mais adequada computacionalmente.
Vimos neste exemplo também, que mesmo em situações simples os intervalos baseados na função deviance são de difícil obtenção e requerem algoritmos numéricos para sua obtenção. Porém de forma geral são mais realistas, no sentido de representar melhor a incerteza associada a estimação do parâmetro e possuírem propriedades ótimas.