Chapter 5 Modelos de regressão

Modelos estocásticos têm sido amplamente utilizados tanto na comunidade científica como no mundo dos negócios em geral. Estudos de mercado usando modelos altamente estruturados, modelos de predição em séries financeiras, análises de componentes de solos para agricultura de precisão, mapeamento de doenças, modelos ecológicos, ambientais e climáticos são algumas das áreas de aplicações de tais modelos, entre tantas outras. De todos os métodos estatísticos, os modelos de regressão talvez sejam o mais amplamente utilizados na prática. Nestes modelos procura-se explicar, ao menos parcialmente, a variabilidade de uma variável considerada como resposta, por outras variáveis chamadas de explicativas ou covariáveis. Procura-se verificar a existência e quantificar o efeito das covariáveis sobre a resposta, embora a relação não seja necessariamente de causa e efeito.

A área de modelos de regressão teve seu início com o tradicional modelo de regressão linear gaussiano, que, seja por sua aplicabilidade e/ou pela facilidade analítica e computacional,
foi e continua sendo largamente utilizado para descrever a associação entre um conjunto de covariáveis e uma variável resposta. Diversas transformações na resposta foram propostas para adaptar a suposição de normalidade. Porém tais modelos não são satisfatórios para respostas discreta como no caso de dados binários, contagens baixas e respostas restritas a certos intervalos como proporções e índices com valores em intervalos limitados.

A modelagem estatística por modelos de regressão recebeu um importante novo impulso desde o desenvolvimento dos modelos lineares generalizados no início da década de \(70\) cujo marco inicial é o trabalho de Nelder and Wedderburn (1972) que estendeu de uma forma mais geral a classe de modelos de regressão, acomodando sob a mesma abordagem diversas distribuições agrupadas na forma da família exponencial. Variáveis resposta binárias e de contagens foram as que receberam mais atenção, talvez pela dificuldade em tratar deste tipo de resposta com transformações do modelo linear gaussiano. Desde então modelos de regressão logística e de Poisson, passaram a ser utilizados nas mais diversas áreas de pesquisa. Nas décadas seguintes e até os dias de hoje o modelo linear generalizado (MLG) tornou-se uma estrutura de referência inicial, canônica, a partir da qual diversas modificações, expansões e alternativas são propostas na literatura. Classes mais amplas de distribuições para resposta, preditores não lineares ou aditivamente lineares, modelagem conjunta de média e dispersão, adição de variáveis latentes no preditor são algumas das importantes extensões, às quais adicionam-se métodos para inferência e algorítimos para computação.

Neste capítulo vamos considerar alguns modelos simples de regressão com ilustrações computacionais. No Capítulo seguinte consideramos modelos com extensões com inclusão de efeitos aleatórios.

Considere que \(Y_1, Y_2, \ldots, Y_n\) são variáveis aleatórias independentes e identicamente distribuídas e \(X\) é a matriz de delineamento do modelo conhecida. Um modelo de regressão em notação matricial pode ser escrito da seguinte forma: \[\begin{align*} Y|X &\sim f(\underline{\mu}, \phi) \\ \underline{\mu} &= g(X;\underline{\beta}). \end{align*}\]

A distribuição de probabilidade \(f(\underline{\mu}, \phi)\) da variável resposta é descrita por dois conjuntos de parâmetros, os de locação (média) e os de dispersão (precisão / variância). Por simplicidade de apresentação supomos aqui que o parâmetro de dispersão é comum a todas as observações e o que muda é apenas a média. Esta restrição pode ser flexibilizada, supondo que o parâmetro de dispersão, também possa ser descrito por alguma função das covariáveis que é possível requerendo uma generalização da implementação computacional. %% deveríamos acrescentar um exemplo de um modelo de média e variância!!

Nesta distribuição é muito importante estar atento ao espaço paramétrico de \(\underline{\mu}\) e \(\phi\). O segundo em geral tem como seu espaço paramétrico os reais positivos, já que, o parâmetro de variabilidade tem que ser necessariamente positivo. Para a parte de média devemos ter mais cuidado, uma vez que a função \(g(\cdot)\) deve mapear o preditor linear ou não-linear, que pode assumir qualquer valor real, para o espaço paramétrico de \(\underline{\mu}\). Por exemplo, se estamos trabalhando com dados de contagens onde o vetor \(\underline{\mu}\) representa o parâmetro da distribuição de Poisson. A função \(g(\cdot)\) deve então mapear dos reais para os reais positivos. Em outra situação, por exemplo com dados restritos ao intervalo \((0,1)\), a função \(g(\cdot)\) deve mapear dos reais para o intervalo unitário e assim de forma análoga para outros espaço paramétricos.

Note que para a declaração completa do modelo são necessárias duas suposições. A primeira se refere a distribuição de probabilidade atribuída a variável resposta, neste caso \(f(\underline{\mu}, \phi)\). A segunda é a definição de uma função \(g(\cdot)\) fazendo com que o preditor linear ou não-linear, que pode apresentar qualquer valor nos reais, seja mapeado adequadamente para o espaço paramétrico da parte de média do modelo.

A função \(g(\cdot)\) deve ser duplamente diferenciável. Uma restrição adicional comum é que seja estritamente monótona, porém em modelos não-lineares, isso nem sempre é necessário. Esta função tem como seus argumentos a matriz de delineamento \(X\) conhecida e os parâmetros \(\underline{\beta}\) desconhecidos a serem estimados. Sendo a função \(g(\cdot)\) definida e mapeando os valores do preditor, seja ele linear ou não, para espaço paramétrico de \(\underline{\mu}\), o modelo está composto e é passível de ter seus parâmetros estimados pela maximização da função de verossimilhança.

Um fato que pode passar desapercebido é com relação ao suporte da distribuição concordar ou não com os possíveis valores do fenômeno em estudo. Por exemplo, ao estudar o peso de animais é comum atribuir o modelo gaussiano, porém este modelo tem como suporte os reais, enquanto que o fenômeno varia apenas nos reais positivos. Nestes casos a usual justificativa prática é que a probabilidade atribuída a parte negativa é tão pequena que é desprezível na prática.

Uma outra situação é quando trabalhamos com uma variável resposta restrita ao intervalo unitário. Podemos definir como função \(g(\cdot)\) o inverso da função logit e vamos estar mapeando a média do modelo ao intervalo unitário compatível com os dados. Porém, na escolha da distribuição nem sempre isso é feito. É comum por exemplo, encontrar aplicações de modelos não-lineares atribuindo a distribuição gaussiana para \(f(\underline{\mu},\phi)\) que tem suporte nos reais e em desacordo com os dados restritos a algum intervalo. Apesar deste tipo de construção não ser incomum em aplicações, é recomendado atribuir uma distribuição de probabilidade que tenha suporte concordante com o campo de variação da variável resposta. No caso de variável resposta restrita ao intervalo unitário, a distribuição Beta ou Simplex seriam opções razoáveis. Tal fato motiva um dos Exemplo na Sessão 5.2. Quando pensamos na concordância entre dados e modelos é mais natural atribuir ao fenômeno uma distribuição cujo suporte, concorde com o campo de variação do fenômeno.

Dado a relevância de modelos de regressão em aplicações nas mais diversas áreas do conhecimento, neste capítulo vamos mostrar como implementar a estimação de alguns modelos de regressão mais usuais como regressão de Poisson, Simplex e não-linear gaussiano. Vamos explorar o algoritmo de Newton-Raphson no modelo de regressão Poisson, para o modelo Simplex, vamos explorar o conceito de verossimilhança concentrada e exemplificar como usar a função escore obtida analiticamente dentro do algoritmo BFGS implementado na função optim. No último modelo vamos tratar tudo numericamente apenas como uma implementação simplificada. Como material adicional apresentamos a implementação computacional de um modelo simple para um processo de Poisson não homogêneo e um estudo de caso com um modelo de regressão para análise de um experimento com contagens subdispersas.

5.1 Regressão Poisson

Em situações onde a resposta é discreta na forma de contagens, escolha de distribuição para variável resposta recai, ao menos inicialmente, sobre a distribuição de Poisson. Conforme mencionado anteriormente, um modelo de regressão qualquer é descrito por duas suposições: a distribucional, que se refere a distribuição de probabilidade atribuída a variável resposta e a uma função \(g(\cdot)\), que liga o preditor à média desta distribuição. No caso do modelo de regressão de Poisson a distribuição tem a seguinte forma,

\[ P(Y = y) = \frac{\exp\{- \lambda\} \lambda^y}{y!}, \quad \text{ em que } \quad \lambda \ge 0 \quad \text{ e } y = 0,1,2 \ldots . \]

No modelo Poisson o parâmetro indexador \(\lambda\) corresponde à esperança de \(Y\). O modelo é um caso particular da família de MLG em que temos apenas a componente de média, já que a variância é igual a média. O parâmetro \(\lambda\) deve ser maior que zero e portanto devemos escolher uma função \(g(.)\) que mapeie dos reais aos reais positivos e a escolha usual para regressão Poisson é a exponencial. No contexto de modelos lineares generalizados pode-se mostrar que a função de ligação canônica para modelo Poisson é a função logaritmo cuja a inversa é a exponencial, por isso sua popularidade. Resumindo, supomos que \(\underline{Y} \sim P(\underline{\lambda})\) e que \(\underline{\lambda} = \exp\{X \underline{\beta}\}\) com a suposição adicional que o preditor é linear. Com isso, chegamos ao modelo de regressão de Poisson.

Expressões genéricas para função de verossimilhança, escore e informação, assim como algoritmos para estimação dos parâmetros são disponíveis para toda classe de MLG. Entretanto como nosso objetivo aqui é ilustrar as computações vamos considerar o caso da Poisson individualmente. A função de log-verossimilhança escrita em formato matricial é dada por,

\[ l(\underline{\beta}, \underline{y}) = - 1^\top g( X \underline{\beta}) + \underline{y}^\top X \underline{\beta} + 1^\top \log(\underline{y} !). \]

Derivando em relação ao vetor de parâmetros \(\underline{\beta}\) temos a função escore.

\[ U(\underline{\beta}) = \left( \underline{y} - \exp\{X \underline{\beta}\} \right)^\top X \]

Derivando novamente obtemos a matriz de informação observada em que \(diag(X \underline{\beta})\) denota uma matrix diagonal com elementos \(\underline{\lambda} = X \underline{\beta}\):

\[ I_o(\underline{\beta}) = - X^\top [diag(\exp\{X \underline{\beta}\})] X . \]

Com isso temos todos os elementos para montar o algoritmo de Newton-Raphson e encontrar as estimativas de máxima verossimilhança para o vetor \(\underline{\beta}\).

Para exemplificar o processo vamos considerar dados simulados supondo que \(X \underline{\beta}\) tem a forma $ _0 + _1 x_i $, em que \(x_i\) é uma covariável com valores conhecidos. Nas simulações a covariável assume \(n=10, 50\) e \(100\) valores igualmente espaçados entre 0 e 5. Assim, o modelo tem apenas dois parâmetros \(\underline{\beta} = (\beta_0, \beta_1)\). O código abaixo apresenta uma função para simular realizações deste modelo e
mostramos o comando para gerar o conjunto de dados com \(n=10\).

Código 5.1 Função para simular variáveis aleatórias de uma modelo de regressão de Poisson.

simula.poisson <- function(formula, beta){
  X <- model.matrix(formula)
  lambda <- exp(X %*% beta)
  y <- rpois(nrow(X), lambda=lambda)
  return(data.frame(y=y, X))}

set.seed(123)
cov <- seq(0, 5, length=10)
dados10 <- simula.poisson(~cov, c(2,0.5))

A Figura 5.1 apresenta a superfície de log-verossimilhança em escala de exata e pela aproximação quadrática, para diferentes tamanhos de amostras. As linhas de contorno definem regiões de confiança que correspondem aos quantis 99, 95, 90, 70, 50, 30, 10 e 5 % de distribuição \(\chi^2_{2}\). O ponto indica o valor verdadeiro do parâmetro. Note-se que os gráficos não estão na mesma escala.

Figura 5.1: Superfície de deviance para diferentes tamanhos de amostra - Regressão Poisson, detalhes no texto.

Podemos perceber que a aproximação quadrática é excelente para os dois parâmetros, o que era esperado, já que, se tratam de parâmetros de média. Entretanto, mesmo esses parâmetros podem ter comportamento assimétrico em algumas situações, como por exemplo, na presença de dados censurados. A relação entre os dois parâmetros também é clara nos gráficos mostrando que os parâmetros não são ortogonais. Note que com o aumento do tamanho da amostra os contornos vão ficando menores, mais concentrados em torno do verdadeiro valor do parâmetro, sugerindo nesta ilustração a propriedade assintótica de consistência e não-viés.

Seguindo com o processo de inferência podemos usar o algoritmo de Newton-Raphson para encontrar as estimativas de máxima verossimilhança de \(\beta_0\) e \(\beta_1\), para isto precisamos escrever duas funções, a escore() e a hessiana() conforme código 5.2. Definimos a função hessiana de duas maneiras na liguagem R. Na primeira programamos diretamente como na expressão. Na sequência reescrevemos a função evitando usar a matriz completa de pesos já que apenas os elementos fora da diagonal são nulos e portanto desnecessários.

Código 5.2 Função escore e hessiana para a regressão de Poisson.

## Função escore
escore <- function(par, formula, dados){
  mf <- model.frame(formula, dados)
  X <- model.matrix(formula, data=mf)
  esco <- crossprod(model.response(mf) - exp(X %*% par), X)
  return(drop(esco))
}

## Hessiana ("naïve")
hessiano <- function(par, formula, dados){
  X <- model.matrix(formula, data=dados)
  mat <- matrix(0, nrow(X), nrow(X))
  diag(mat) <- -exp(X%*%par)
  H <- t(X) %*% mat %*% X
  return(H)
}

## Hessiana (equivalente a anterior)
hessiano <- function(par, formula, dados){
  X <- model.matrix(formula, data=dados)
  H <- crossprod(X * -exp(drop(X%*%par)),  X)
  return(H)
}

Usando o algoritmo de Newton-Raphson já apresentado em 3.5, temos as estimativas para o conjunto simulado com \(n=10\).

(beta10 <- NewtonRaphson(initial=c(0,0), escore=escore, 
                         hessiano=hessiano, max.iter=1000, 
                         formula=y~cov, dados=dados10))

## (Intercept)         cov 
##       2.229       0.428

Para a construção dos intervalos de confiança assintóticos, basta avaliar a inversa da matriz hessiana no ponto encontrado e os erros padrão das estimativas são dados pelas raízes quadradas dos elementos diagonais.

Io <- -hessiano(par=beta10, formula=y~cov, dados=dados10)
Io

##             (Intercept)  cov
## (Intercept)         338 1182
## cov                1182 4796

(erro.padrao <- sqrt(diag(solve(Io))))

## (Intercept)         cov 
##      0.1465      0.0389

Lembrando que as variâncias de \(\hat{\beta_0}\) e \(\hat{\beta_1}\) são dadas pelos termos da diagonal da inversa da matriz de informação observada, temos pela distribuição assintótica do EMV que um intervalo de \(95\%\) de confiança para \(\beta_0\) e \(\beta_1\) poderia ser obtido por:

beta10[1] + c(-1,1)*qnorm(0.975)*erro.padrao[1]

## [1] 1.94 2.52

beta10[2] + c(-1,1)*qnorm(0.975)*erro.padrao[2]

## [1] 0.351 0.504

Nossos resultados coincidem com as estimativas retornadas pela função glm() do R.

beta10.glm <- glm(y ~ cov, family=poisson, data=dados10)
coef(beta10.glm)

## (Intercept)         cov 
##       2.229       0.428

summary(beta10.glm)$coef

##             Estimate Std. Error z value Pr(>|z|)
## (Intercept)    2.229     0.1465    15.2 2.97e-52
## cov            0.428     0.0389    11.0 3.98e-28

confint(beta10.glm, type="quad")  

##             2.5 % 97.5 %
## (Intercept) 1.933  2.507
## cov         0.353  0.505

Os intervalos acima podem ser inadequados quando os parâmetros são não ortogonais por considerar isoladamente a curvatura em cada direção. O grau de não ortogonalidade também é influenciado pela da ordem de magnitude das covariáveis e consequentemente dos parâmetros. Uma primeira alternativa é a obtenção dos intervalos através de verossimilhança (ou deviance) perfilhada, que tipicamente fornece intervalos mais largos e por vezes assimétricos. Esta solução pode ser computacionalmente mais cara ou mesmo proibitiva dependendo da quantidade de observações e parâmetros no modelo.

confint(beta10.glm)

##             2.5 % 97.5 %
## (Intercept) 1.933  2.507
## cov         0.353  0.505

Uma outra solução é utilizar covariáveis centradas para obter verossimilhanças (aproximadamente) ortogonais. Além disto as covariáveis podem ainda ser escalonadas para que os coeficientes tenham ordem de grandeza comparáveis e a função tenha contornos ao menos aproximadamente circulares. Desta forma, os coeficientes são inicialmente estimados pontualmente e por intervalo para variáveis transformadas. Posteriormente, as estimativas são transformadas para escala original pela equação que define a reparametrização.

Com isso, exemplificamos a construção dos cálculos computacionais do modelo de regressão de Poisson. Procedemos a estimação por máxima verossimilhança, obtivemos o vetor e a matriz que possibilitaram o uso do algoritmo de Newton-Raphson. Vimos também que a aproximação quadrática no caso do modelo Poisson é bastante acurada, sendo que em nossos exemplos é visualmente difícil encontrar diferença entre ela e a exata mesmo para a amostra de tamanho 10. Usando resultados assintóticos construímos intervalos de confiança de duas formas diferentes. Além disso, com os resultados obtidos estamos aptos a proceder os testes de hipóteses, por exemplo, \(H_0 :\beta_1 = 0\) contra \(H_1 : \beta_1 \neq 0\). Neste caso, poderíamos usar o tradicional teste de Wald, teste escore ou mesmo o teste de razão de verossimilhança.

5.2 Regressão Simplex

Em situações práticas podemos estar diante de variáveis restritas ao intervalo \((0,1)\), como taxas, proporções e índices. O exemplo que motiva essa sessão vem da área de ciências sociais na qual é comum a mensuração de variáveis latentes (não observáveis) que muitas vezes buscam medir qualidade, através de indicadores indiretos sobre o fenômeno latente. Um exemplo deste tipo de análise é o IDH - Índice de Desenvolvimento Humano, preconizado pela ONU - Organização das Nações Unidas, em todo o mundo.

Estes índices que tradicionalmente, por construção, resultam sempre em valores no intervalo unitário, buscam medir indiretamente o nível de desenvolvimento de um país. O índice pode ser adaptado como o IDH-M (Índice de Desenvolvimento Humano - Municipal) para municípios, estados ou qualquer aglomeração de indivíduos, como por exemplo, bairros de uma cidade. A importância em ressaltar que a construção leva a um número no intervalo unitário, é a de que o índice é expresso como uma nota em uma escala comum, permitindo a comparação entre países, estados, municípios ou bairros.

Com foco em tais situações, selecionamos para este exemplo o Índice de Qualidade de Vida de Curitiba (IQVC). Este índice é composto por \(19\) indicadores separados em \(4\) áreas temáticas: Habitação, Saúde, Educação e Segurança. Estes indicadores buscam de forma indireta medir o nível de vida da população residente em cada um dos \(75\) bairros da cidade. A metodologia para sua construção segue as premissas do IDH, e como tal resulta sempre em valores no intervalo unitário. Para sua construção é utilizada a base de microdados do Censo 2000, disponibilizada pelo IBGE (Instituto Brasileiro de Geografia e Estatística). Um interesse comum é relacionar o IQVC com a renda média do bairro medida em salários mínimos vigentes na época da pesquisa, neste caso ano de 2000. Os dados são disponibilizados pelo IPPUC/PR (www.ippuc.org.br) e uma versão resumida está disponível no arquivo simplex.txt dos complementos online.

Para a construção do modelo de acordo com a abordagem que utilizamos neste material, é necessário fazer duas suposições, como nos MLG’s usuais, a primeira a respeito da distribuição de probabilidade atribuída a variável resposta e a segunda referente a função \(g(\cdot)\) que vai mapear o preditor linear ou não ao espaço paramétrico induzido pela distribuição suposta. Para este exemplo vamos supor a distribuição como sendo Simplex e a função \(g(\cdot)\) como a inversa da função logit, comum em modelos lineares generalizados. A apresentação do modelo aqui baseia-se no trabalho de Miyashiro (2008).

A função densidade de probabilidade Simplex é indexada por dois tipos de parâmetros locação \(\mu \in (0,1)\) e dispersão \(\sigma^2 > 0\). Ambos podem ser decompostos em função de covariáveis observadas. Uma variável aleatória \(Y\) que segue o modelo Simplex tem função densidade dada por \[ \begin{equation} \tag{5.1} f(y; \mu, \sigma^2) = [ 2 \pi \sigma^2 {y(1-y)}^3]^{-1/2} \exp \left\{ - d(y;\mu)/2\sigma^2 \right\}, \quad y \in (0,1), \end{equation} \] em que

\[\begin{equation*} d(y;\mu) = \frac{(y - \mu)^2}{y (1-y) \mu^2 (1- \mu)^2} . \end{equation*}\]

Sejam \(Y_1, Y_2, \ldots, Y_n\) variáveis aleatórias independentes, sendo cada \(Y_i \sim S(\mu_i, \sigma^2)\), \(i = 1,2, \ldots, n.\) O modelo de regressão Simplex é definido pela densidade (5.1), sendo as médias \(\mu_i\) dadas por \[\begin{equation*} \mu_i = g( x_i^\top \underline{\beta}) = g(\eta_i) \end{equation*}\] em que \(g(\cdot)\) é uma função que transforma valores dos reais ao intervalo unitário, \(\underline{\beta} = (\beta_1, \beta_2, \ldots, \beta_p)^\top\) é o vetor de parâmetros da regressão \((\underline{\beta} \in \Re^p)\), \(x_i^\top = (x_{i1}, x_{i2}, \ldots, x_{ip})^\top\) são os valores conhecidos de \(p\) covariáveis e \(\eta_i\) neste caso é o preditor linear. Poderíamos, sem perda de generalidade definir o preditor como \[\begin{equation*} h(\mu_i) = x_i^\top \underline{\beta} = \eta \end{equation*}\] onde agora \(h(\cdot)\) é uma função de ligação que transforma do \((0,1)\) em \(\Re\), dependendo da situação pode ser mais simples definir de uma forma ou de outra. No caso Simplex vamos definir a função \(h(\cdot)\) como sendo a função \(logit\) que facilita bastante a obtenção do vetor escore. O objetivo deste exemplo é mostrar como usar os otimizadores numéricos implementados na função optim(), porém usando o vetor escore obtido analiticamente.

Dada a função densidade de probabilidade, podemos facilmente obter a função de log-verossimilhança, \[ l_i(\mu_i,\sigma^2) = - 0.5 [\log(2\pi) + \log(\sigma^2) + 3 \log \{ y_i (1 - y_i)\} + d(y_i;\mu_i)/\sigma^2]. \]

Temos que \(h(\mu_i) = x_i^\top \underline{\beta} = \eta_i\), então para obter o vetor escore precisamos derivar em relação a cada \(\beta_p\).

\[\begin{equation*} \frac{\partial l(\underline{\beta}, \sigma^2)}{\partial \beta_p} = \sum_{i=1}^n \frac{\partial l_i(\mu_i, \sigma^2)}{\partial \mu_i} \frac{\partial \mu_i}{ \partial \eta_i} \frac{\partial \eta_i}{\partial \beta_i}. \end{equation*}\]

Para obter o vetor escore para a parte de média precisamos de três componentes, o primeiro é: \[\begin{eqnarray} & \frac{\partial l(\mu_i, \sigma^2)}{\partial \mu_i} = -\frac{1}{2 \sigma^2} \frac{\partial}{\partial \mu_i} d(y_i, \mu_i) = \\ \nonumber & = \sigma^{-2} \left[\underbrace{ \frac{(y_i - \mu_i)}{(1-\mu)^2 \mu^2 (1-y)y} + \frac{(y_i - \mu_i)^2}{(1-\mu)^2 \mu^3 (1-y)y} - \frac{ (y_i - \mu_i)^2}{(1-\mu_i)^3 \mu^2 (1 - y_i)y_i} }_u \right] , \end{eqnarray}\] o segundo, \[ \frac{\partial \mu_i}{ \partial \eta_i} = \frac{1}{g'(\mu_i)} = \mu_i (1 - \mu_i) , \] e o terceiro, \[ \frac{\partial \eta_i}{\partial \beta_i} = x_{ip} . \]

Em notação matricial, a função escore para \(\underline{\beta}\) é dada por \[ U_{\underline{\beta}}(\underline{\beta}, \sigma^2) = \sigma^{-2} X^\top T u, \] onde \(X\) é uma matriz \(n \times p\), de delineamento do modelo, \(T = diag\{ 1/g'(\mu_1), \ldots, 1/g'(\mu_i) \}\) e \(u^\top = (u_1, \ldots, u_n)\top.\)

A função escore para \(\sigma^2\) é facilmente obtida, derivando \(l(\underline{\beta}, \sigma^2)\) em relação a \(\sigma^2\), \[\begin{equation*} U_{\sigma^2}(\underline{\beta}, \sigma^2) = -\frac{n}{2 \sigma^2} + \frac{1}{2 \sigma^4} \sum_{i=1}^n d(y_i; \mu_i). \end{equation*}\]

Note que podemos obter \(\hat{\sigma}^2\) analiticamente, sua equação é dada por \[ \hat{\sigma}^2 = \frac{1}{n} \sum_{i=1}^n d(y_i, \hat{\mu}_i) . \]

Com isso temos todos os elementos necessários para a implementação computacional do modelo de regressão Simplex. Não há uma implementação da densidade Simplex entre as funções básicas do R. Começamos então definindo uma função para densidade da Simplex.

Código 5.3 Função densidade de probabilidade para uma variável aleatória de distribuição Simplex.

dsimplex <- function(y, mu, sigma, log=TRUE){
  dis <- (y-mu)^2 / (y*(1-y)*mu^2 *(1-mu)^2)
  dsim <- -0.5*log(2*pi) -0.5*log(sigma) - 
                (3/2)*log(y*(1-y)) - (1/(2*sigma))*dis
  if(log == FALSE){dsim <- exp(dsim)}
  return(dsim)}

Dada a aplicação teremos o vetor \(\underline{\beta} = (\beta_0, \beta_1)\) e então o modelo de regressão Simplex em R é apresentado no código abaixo. Definimos a função de ligação logit para \(h(\cdot) = g^{-1}(\cdot)\) e sua inversa \(g(\cdot)\). Note que como o parâmetro \(\sigma^2\) tem solução analítica e depende apenas de \(\mu_i\) não precisamos maximizar numericamente em relação a este parâmetro, estamos novamente usando uma log-verossimilhança concentrada. Basta substituirmos seu estimador na expressão da log-verossimilhança. Em nossas implementações este procedimento foi fundamental para conseguir estabilidade nos resultados do algoritmo de maximização da verossimilhança.

Código 5.4 Função de log-verossimilhança para o modelo de regressão Simplex.

inv.logit <- function(x, lambda){ 1/(1+exp(-x)) }
modelo.simplex <- function(b0, b1, formula, data){
  mf <- model.frame(formula, data=data)
  y <- model.response(mf)
  X <- model.matrix(formula, data=mf)
  mu <- inv.logit(X%*%c(b0,b1))
  d0 <- ((y-mu)^2)/(y*(1-y)*mu^2*(1-mu)^2)
  sigma <- sum(d0)/length(y)
  ll <- sum(dsimplex(y, mu=mu, sigma=sigma))
  return(-ll)
}

O próximo passo é implementar a função escore já obtida, note novamente que ela é função apenas de dois parâmetros \(\beta_0\) e \(\beta_1\), uma vez que tenhamos estes substituímos na expressão de \(\hat{\sigma}^2\) e o usamos na expressão do vetor escore.

Código 5.5 Função escore para o modelo de regressão Simplex.

escore <- function(b0, b1, formula, data){
  mf <- model.frame(formula, data=data)
  y <- model.response(mf)
  X <- model.matrix(formula, data=mf)
  eta <- X%*%c(b0,b1)
  mu <- inv.logit(eta)
  d0 = ((y - mu)^2) / (y*(1-y)*mu^2 * (1-mu)^2)
  sigma <- sum(d0)/length(y)
  T <- diag(c(mu*(1-mu)))
  u <- (1/(sigma*(1-mu)*mu))*(-((y-mu)^2/((1-mu)^2*mu^2)) +  
         (((y - mu)^2)/((1-mu)^2*mu^2))+((y-mu)/((1-mu)^2*mu^2)))
  es <- (crossprod(X,T) %*% u)/sigma
  return(as.numeric(-es))
}

Com isto, estamos aptos a passar a log-verossimilhança e o vetor escore para a optim e obter as estimativas de máxima verossimilhança para \(\beta_0\) e \(\beta_1\), com estas substituímos na expressão de \(\hat{\sigma}^2\) e concluímos o processo de estimação. Antes disso, precisamos do conjunto de dados que será analisado. O arquivo chamado simplex.txt traz o conjunto para a análise. O código abaixo lê a base de dados e apresenta um pequeno resumo. A Figura 5.2 apresenta uma análise exploratória gráfica, com um histograma e um diagrama de dispersão relacionando o IQVC com a renda média do bairro em salários mínimos que foi divido por \(10\) para evitar problemas numéricos.

dados <- read.table("simplex.txt",header=TRUE)
head(dados)

##   ID     y MEDIA
## 1 10 0.642  1.47
## 2  6 0.764  1.53
## 3 70 0.858  1.91
## 4 69 0.669  2.16
## 5 62 0.846  1.73
## 6 61 0.786  1.72

O conjunto de dados contêm apenas três colunas, a primeira denominada \(ID\) apenas identifica os diferentes bairros, a coluna \(y\) apresenta o Índice de Qualidade de Vida de Curitiba (IQVC) e a coluna \(MEDIA\) apresenta a renda média do bairro em salários mínimos dividido por \(10\).

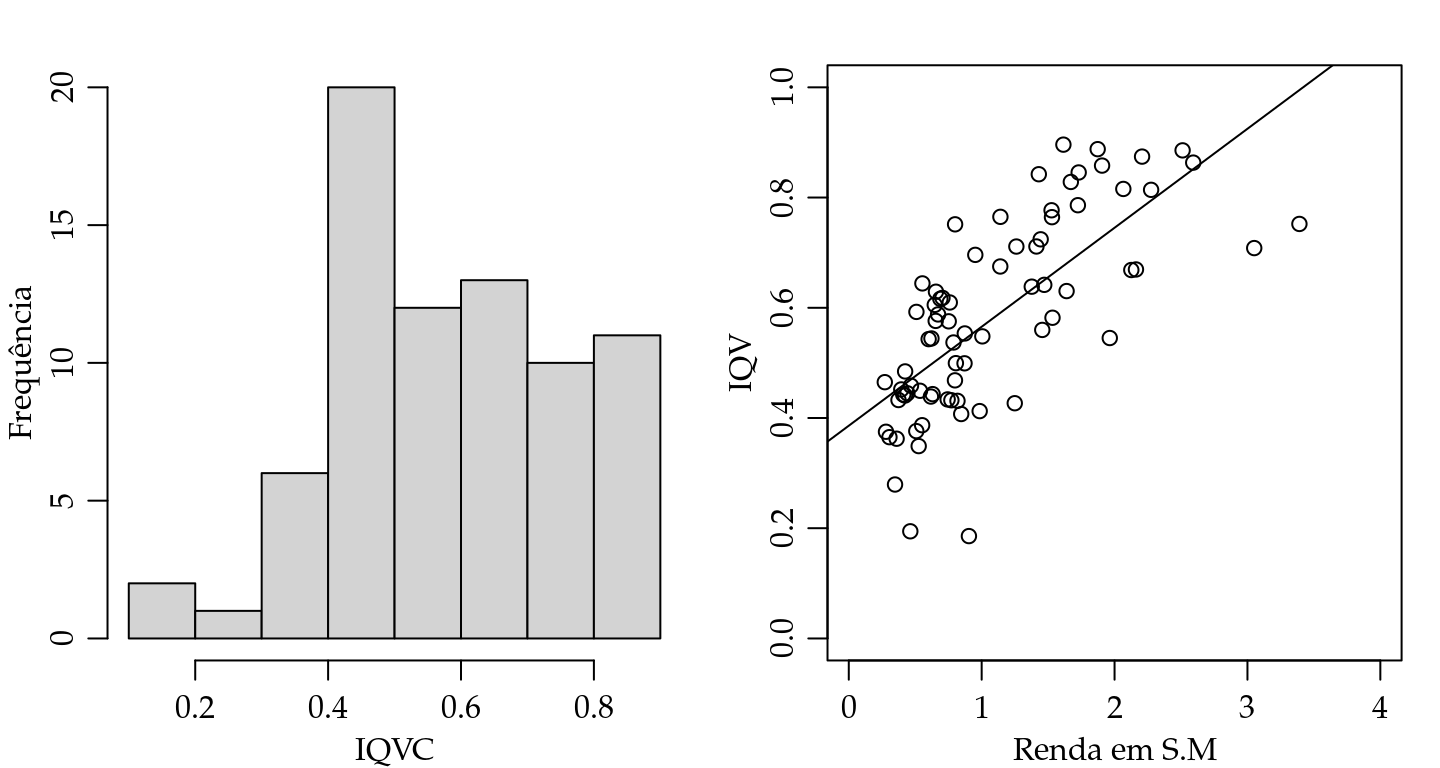
Figura 5.2: Histograma e diagrama de dispersão - IQVC.

Para o ajuste do modelo Simplex, vamos novamente usar as facilidades do pacote bbmle que usa internamente a função optim(). O ajuste é dado no seguinte código.

require(bbmle)
simplex.logit.gr <- mle2(modelo.simplex, start=list(b0=0,b1=0),
                         gr=escore, method="BFGS",
                         data=list(formula=y~MEDIA, data=dados))

A única diferença é no uso do argumento \(gr\) onde é passada a função escore com exatamente os mesmos argumentos adicionais usados na função de log-verossimilhança. A função optim() tem quatro otimizadores básicos: Nelder-Mead, gradiente conjugado, BFGS e simulating annealing. O uso de gradiente analítico só é possível nos algoritmos BFGS e gradiente conjugado.

O resumo tradicional do modelo pela função summary(), traz os erros padrões que são usados para a construção de intervalos de confiança assintóticos, que podem ser obtidos diretamente pela função confint(..., method="quad").

summary(simplex.logit.gr)

## Maximum likelihood estimation
## 
## Call:
## mle2(minuslogl = modelo.simplex, start = list(b0 = 0, b1 = 0), 
##     method = "BFGS", data = list(formula = y ~ MEDIA, data = dados), 
##     gr = escore)
## 
## Coefficients:
##    Estimate Std. Error z value   Pr(z)    
## b0  -0.3998     0.1591   -2.51   0.012 *  
## b1   0.6836     0.0992    6.89 5.4e-12 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## -2 log L: -103

confint(simplex.logit.gr, method="quad")

##     2.5 %  97.5 %
## b0 -0.712 -0.0881
## b1  0.489  0.8780

Deixamos como exercício para o leitor obter o intervalo de confiança para \(\sigma^2\) e os perfis de verossimilhança para \(\beta_0\) e \(\beta_1\). Para finalizar o exemplo, podemos visualizar o ajuste sobreposto aos dados. Para isto, vamos escrever uma função genérica para gerar os preditos.

Código 5.6 Função para calcular os valores preditos para um modelo de regressão Simplex.

my.predict <- function(modelo, formula, newdata){
  X <- model.matrix(formula,data=newdata)
  beta <- coef(modelo)[1:ncol(X)]
  preditos <- inv.logit(X%*%beta)
  return(preditos)
}

Usando a função my.predict() obtemos os valores preditos pelo modelo para rendas em uma sequência de valores.

preditos <- my.predict(simplex.logit.gr, formula=~MEDIA, 
                       newdata= data.frame(MEDIA=seq(0,4,l=500)))

Por fim, plotamos na Figura 5.3 um diagrama de dispersão com as observações e a média predita pelo modelo para a sequência de valores de renda.

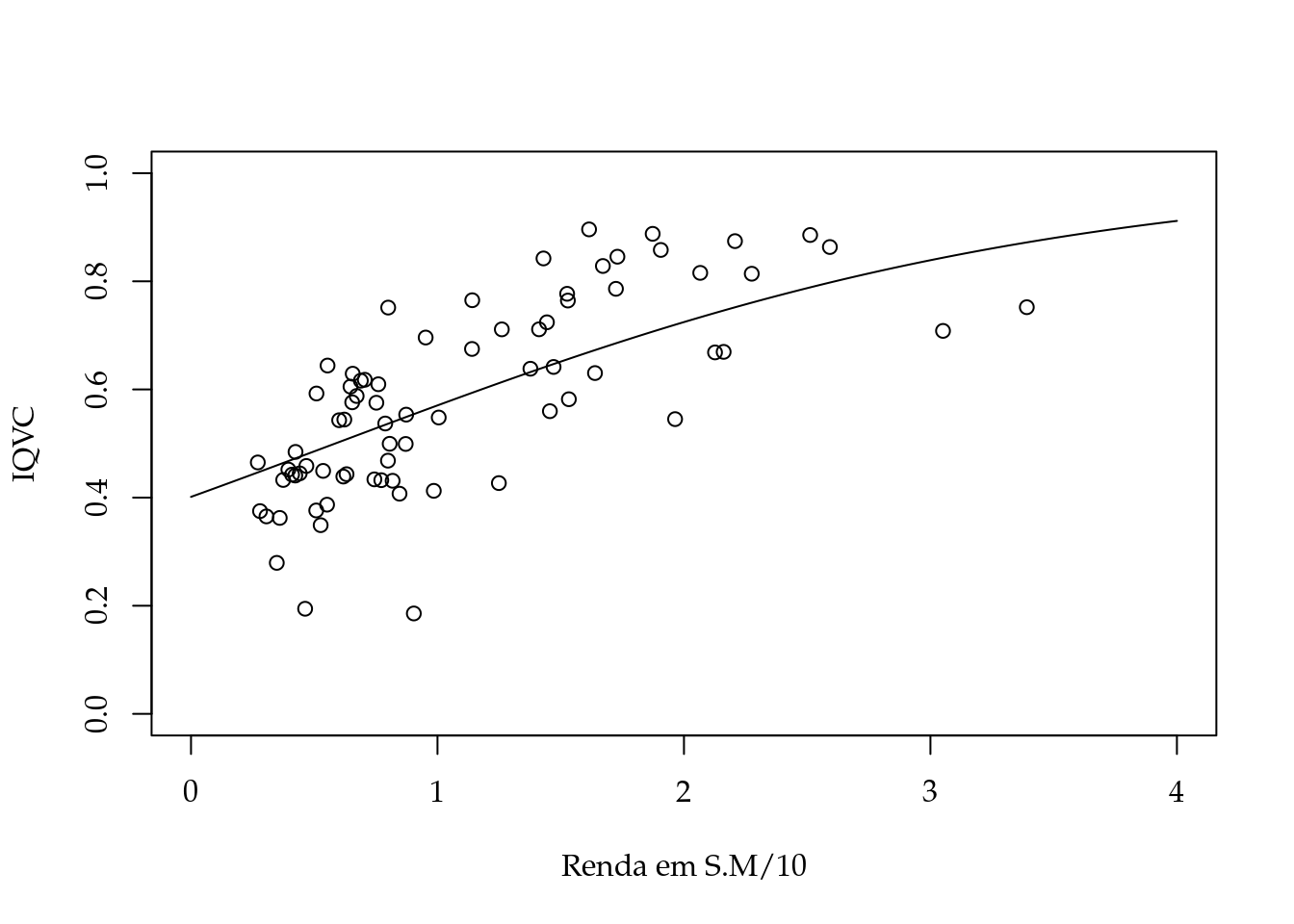
Figura 5.3: Diagrama de dispersão e modelo ajustado - IQVC 2000.

5.3 Modelo contagem-Gama

Contagens são variáveis aleatórias que assumem valores inteiros não negativos. Esses valores representam o número de vezes que um evento ocorre em um domínio fixo contínuo, como um intervalo de tempo ou espaço, ou discreto, como a avaliação de um indivíduo ou setor censitário.

Em análise de dados de contagem o uso do modelo de regressão Poisson tem ocorrência predominante. Esse modelo tem sido uma escolha natural e imediata para essa classe de variável aleatória devido primeiramente à compatibilidade de suporte. Além disso, dados de contagem apresentam certa assimetria em relação à média e variabilidade que depende desse valor médio, duas características que são inerentes ao modelo de regressão Poisson. Entretanto, também inerente à esse modelo, está a forte suposição de equidispersão, ou seja, a da variância esperada ser igual à média esperada.

Afastamentos dessa suposição são frequentemente observadas em análise de dados, principalmente a superdispersão. Superdispersão corresponde à variância ser maior que a média. Isso pode ser resultado de

• ausência de covariáveis importantes, sejam ausentes por que não foram observadas ou ausentes porque não foram declaradas, como por exemplo a omissão da interação entre covariáveis;
• excesso de zeros, que na verdade trata-se de uma mistura de distribuições em que parte dos zeros são gerados pelo processo Poisson e parte é gerado por um processo Bernoulli;
• diferentes amplitudes de domínio, quando eventos são contados em intervalos de tempo ou espaço em que o tamanho desses intervalos é variável e não considerado na análise, geralmente como offset.
• efeito aleatório à nível de observações ou grupos de observações, quando existe no preditor teórico um componente estocástico, à nível de observações ou grupos de observação (blocos), \(\ldots\) .

Note que em todas as situações acima foram introduzidos processos que geram mais variabilidade (mistura com Bernoulli, efeito aleatório) ou que não permitem explicar a variabilidade existente (desconhecimento dos domínios, falta de covariáveis ou termos no modelo) de uma variável aleatória Poisson.

Uma forma de relaxar a suposição de equidispersão é generalizar o processo Poisson. Para isso exploramos a relação que existe entre a distribuição Exponencial e a distribuição de Poisson. De maneira bem simplificada, suponha que temos eventos que ocorrem sob um domínio unidimensional de forma que o intervalo entre eventos tenha distribuição Exponencial. Se dividirmos o domínio em intervalos de igual tamanho, o número de eventos por intervalo terá distribuição de Poisson. Então, para generalizarmos a distribuição do número de eventos, basta atribuirmos outra distribuição para o intervalo entre eventos. Exatamente empregando esse raciocínio que Winkelmann (1995) generalizou a distribuição Poisson empregando a distribuição Gama para o intervalo entre eventos. Entretanto, qualquer outra distribuição de suporte positivo poderia ser empregada. O notável e vantajoso da distribuição Gama é que a distribuição Exponencial é um caso particular dela. Ou seja, a distribuição Gama tem a seguinte função densidade de probabilidade \[ \text{Gama}(y; \alpha, \beta) = \frac{\beta^\alpha}{\Gamma(\alpha)}\exp\{-\beta x\}\,x^{\alpha-1}, \] e para \(\alpha= 1\) temos a função densidade de probabilidade da distribuição Exponencial como caso particular \[ \text{Exp}(y; \beta) = \beta\exp\{-\beta x\} . \]

Para entender como as distribuições estão de fato ligadas, pense assim: a variância da Gama é \(\alpha/\beta^2\), logo, menor valor de \(\alpha\) corresponde a menor variância, quer dizer que se concentra uma grande proporção de valores ao redor da média, então intervalos entre eventos serão mais regulares e se dividimos o domínio em intervalos iguais temos um número pouco variável de eventos por intervalo (subdispersão). Por outro lado, maior valor de \(\alpha\) corresponde à maior variância, logo, os intervalos entre eventos são mais variáveis/irregulares, de forma que ao dividir o domínio em intervalos temos um número de eventos por intervalo com maior variância (superdispersão).

Na Figura 5.4 foram representados eventos ocorrendo ao longo de um domínio onde a distribuição dos intervalos entre eventos é Gama com média fixa e igual à 1. Em cada um dos casos os parâmetros usados foram sub:\((\alpha=5, \beta=5)\), equi:\((\alpha=1, \beta=1)\), super:\((\alpha=0.2, \beta=0.2)\) que correspondem às variâncias de 0.2, 1 e 5 respectivamente. As funções densidade de probabilidade estão no topo da Figura. No centro da Figura temos o domínio dividido em intervalos unitários e o número de eventos por intervalo representado. Notamos uma distribuição mais uniforme no sub que nos demais o que está de acordo com a argumentação do parágrafo anterior. Para obter os histogramas foram geradas amostras de 50000 elementos e o intervalo teve amplitude de 10 unidades para quantificação do número de eventos (por isso a média passou a ser 10).

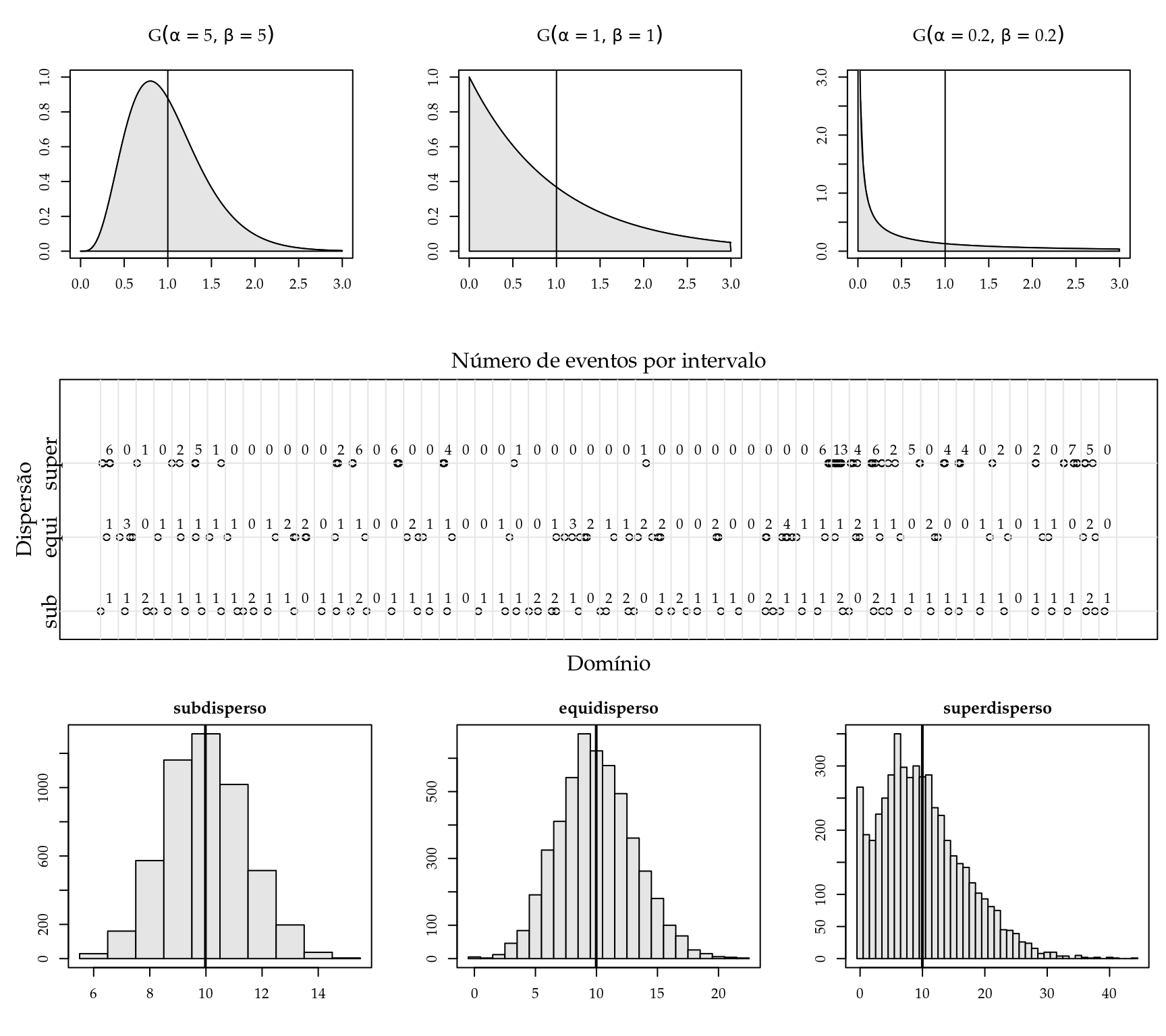
Figura 5.4: Funções densidade de probabilidade para diferentes distribuições de intervalos entre eventos (acima). Eventos distribuídos ao longo de um domínio dividido em intervalos com o número de eventos por intervalo representado (centro). Histogramas do número de eventos por intervalo para cada distribuição de intervalo entre eventos (abaixo).

Winkelmann (1995) obteve que a função de probabilidades de uma variável aleatória de contagem (\(N\)) pode ser escrita como função da distribuição acumulada dos intervalos entre eventos (\(T\)). Assim, para intervalos Gama, a distribuição de probabilidades do número de eventos por intervalo unitário é dada por

\[ \begin{equation} \tag{5.2} P(N=n) = G(1, \alpha n, \beta)-G(1, \alpha(n+1), \beta). \end{equation} \]

A distribuição de \(N\) é superdispersa para \(0<\alpha<1\) e subdispersa para \(\alpha>1\).

Uma vez conhecida a função de probabilidade de uma variável aleatória, podemos fazer a estimação dos parâmetros pelo método da máxima verossimilhança. Tomando a equação (5.2) e estendendo para um modelo de regressão obtemos a seguinte função de log-verossimilhança

\[ \begin{equation} l(y_i; x_i, \alpha, \gamma) = \sum_{i=1}^{n} \log\left( G(1, \alpha y_i, \alpha\exp(x_i^\top\gamma))-G(1, \alpha (y_i+1), \alpha\exp\{x_i^\top\gamma)\} \right). \end{equation} \]

em que \(y_i\) é o número de eventos observado na observação \(i\), \(x_i\) um vetor de covariáveis conhecidas, \(\gamma\) é o vetor de parâmetros associado as covariáveis \(x_i\). No modelo acima estamos descrevendo a média de \(T\) por um modelo de regressão uma vez que \(E(T|x_i) = \alpha/\beta = \exp(-x_i^\top\gamma)\) que manipulando resulta em \(\beta = \alpha\exp(x_i^\top\gamma)\). A média de \(N\) por sua vez pode ser obtida pela seguinte expressão

\[ \begin{equation} \tag{5.3} E(N|x_i) = \sum_{i=1}^{\infty} G(\alpha i, \alpha\exp(x_i^\top\gamma)). \end{equation} \]

Uma variável de contagem importante do estudo de populações de seres vivos é o número de descendentes produzidos durante a vida. Nas espécies vegetais de importância agrícola, fatores que alteram o número de descendentes também têm impacto na produtividade das culturas. Na cultura do algodão (Gossypium hirsutum) a produtividade é função principalmente do número de capulhos produzidos. Ataques de pragas desfolhadoras, por causarem redução da área foliar ou facilitar o desenvolvimento de doenças, podem reduzir a capacidade produtiva da cultura. Para avaliar os efeitos da desfolha, um experimento foi conduzido em casa de vegetação. Em vasos com duas plantas de algodão foram aplicados os níveis de desfolha artificial 0, 25, 50, 75 e 100% de remoção da área foliar (feito com tesoura). A desfolha foi estudada nos estágios fenológicos vegetativo, presença de botão floral, início do florescimento, presença de maça e presença de capulho. Cada combinação desses níveis teve cinco repetições em delineamento completamente casualizado. Ao final do ciclo da cultura, o número de capulhos por vaso foi registrado. Os dados estão no complemento online do texto.

A subdispersão é uma característica facilmente observada no número de capulhos. Ao dispor a variância amostral como função das médias amostrais percebemos que todos os valores ficaram abaixo da linha 1:1 (Figura 5.5), portanto, uma evidência contra a suposição de equidispersão. Nessa situação, o emprego do modelo de regressão Poisson não é adequado e o modelo de regressão contagem-Gama, desenvolvido por Winkelmann (1995), será aplicado. A função de log-verossimilhança do modelo está disponível no código 5.7.

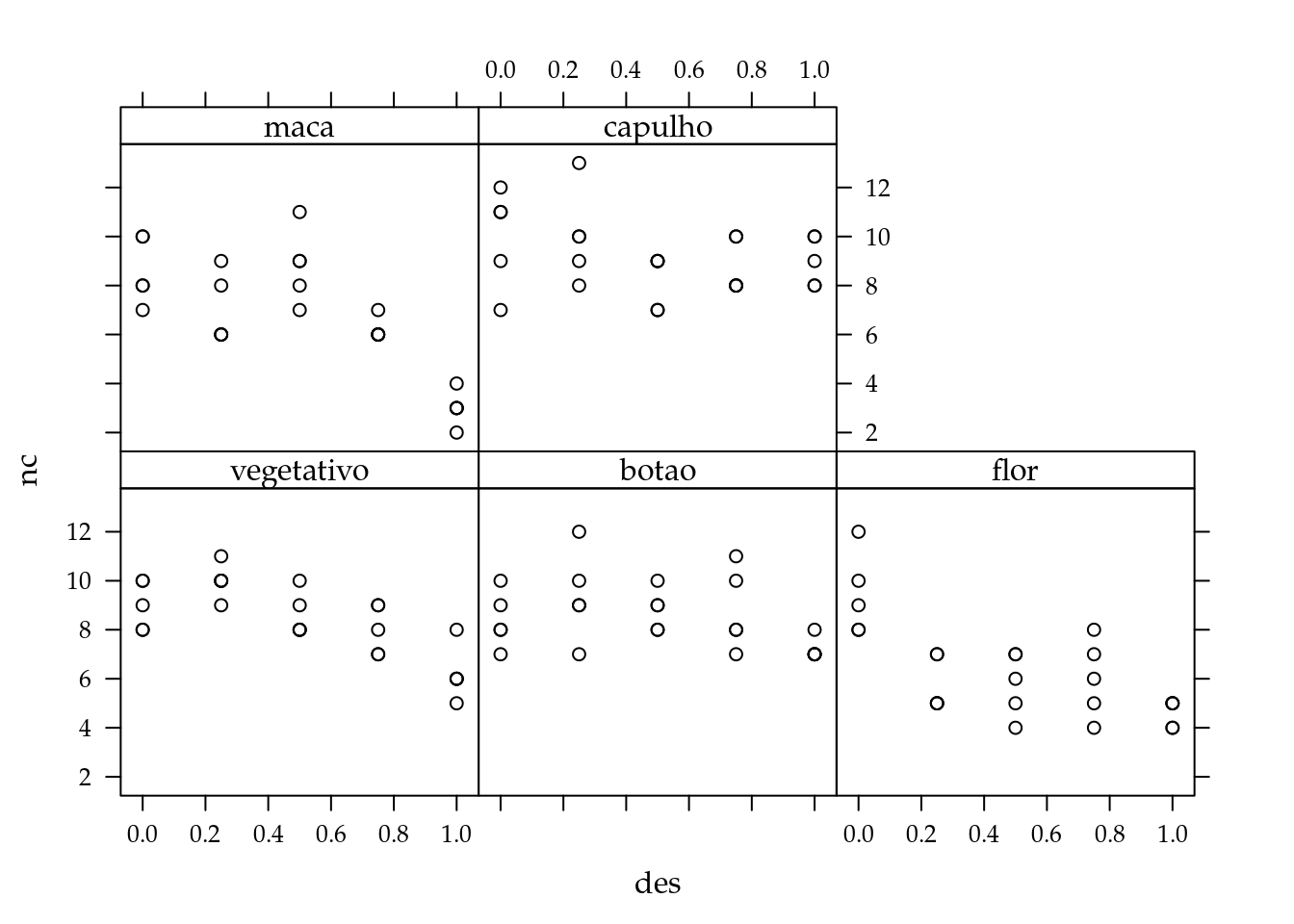
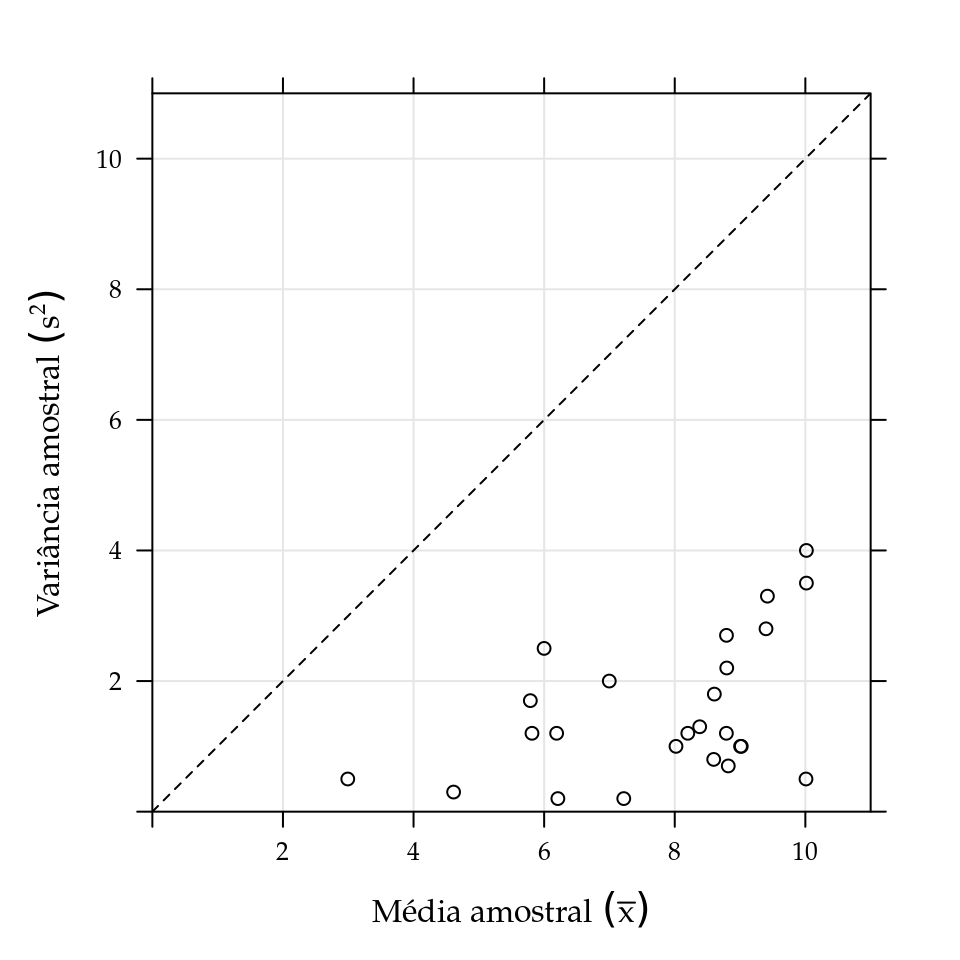
Figura 5.5: Variância amostral em função da média amostral para o número de capulhos do algodão.

Código 5.7 Função de log-verossimilhança para o modelo de regressão contagem-Gama.

ll <- function(theta, y, X){
  ## theta: vetor de parâmetros/estimativas
  ## y: vetor de dados observados
  ## X: matrix de covariáveis associadas aos valores observados
  eXb <- exp(X%*%theta[-1]) #*theta[1]
  ## retorna a log verossimilhança para a amostra
  sum(log(pgamma(1, theta[1]*y, theta[1]*eXb)-
          pgamma(1, theta[1]*(y+1), theta[1]*eXb)))
}

A análise exploratória dos dados indica que o valor médio do número de capulhos depende do estágio e do nível de desfolha de forma não aditiva. Assim, usamos um modelo de interação entre os fatores com polinômio de segundo grau para efeito do nível de desfolha. Dessa maneira, a matriz do modelo é construida por meio da função model.matrix(). Esse modelo considera a estimação de um vetor de 11 parâmetros: intercepto único, efeito linear e efeito quadrático de desfolha por nível de estágio. A estimação usando optim() exige valores iniciais para iniciar o algoritmo. Um conjunto de bons valores iniciais são as estimativas dos parâmetros para o modelo de regressão de Poisson, que obtemos no R com a função glm().

X <- model.matrix(~est:(des+I(des^2)), data=cap)
## estimação modelo Poisson
rp <- glm(nc~est:(des+I(des^2)), data=cap, family=poisson)
## estimação modelo Contagem Gamma
op <- optim(c(alpha=1, coef(rp)), ll, y=cap$nc, 
            X=X, hessian=TRUE, method="BFGS", 
            control=list(fnscale=-1))
# 2*diferença da log-verossimilhança
dll <- c(diff.ll=2*abs(op$value-c(logLik(rp)))); dll 

## diff.ll 
##    94.8

Ao comparar as verossimilhanças do modelo Poisson com o contagem-Gama estamos testanto a hipótese do parâmetro \(\alpha=1\). Vemos que essa hipótese foi rejeitada. De forma complementar ao teste de hipótese, podemos obter o perfil de log-verossimilhança para o parâmetro \(\alpha\) e construir intervalos de confiança. Para isso escrevemos outra função de log-verossimilhança onde \(\alpha\) é fixo e a estimação se dá apenas para os demais parâmentros do modelo (código 5.8). Para fins de comparação, construimos intervalos de confiança baseados na aproximação quadrática da função de log-verossilhança para avaliar a qualidade da aproximação. Nos códigos abaixo tais procedimentos são ilustrados. A função uniroot.all() do pacote rootSolve é empregada para obter os intervalos de confiança baseados no perfil da deviance.

Código 5.8 Função de perfil de log-verossimilhança para o parâmetro \(\alpha\) do modelo de regressão contagem-Gama.

ll.alpha <- function(theta, alpha, y, X){
  ## theta: vetor de parâmetros/estimativas
  ## alpha: escalar do parâmetro alpha fixo
  ## y: vetor de dados observados
  ## X: matrix de covariáveis associadas aos valores observados
  eXb <- exp(X%*%theta) #*theta[1]
  ## retorna a log verossimilhança com um valor FIXO de ALPHA
  sum(log(pgamma(1, alpha*y, alpha*eXb)-
          pgamma(1, alpha*y+alpha, alpha*eXb)))
}

alpha <- sort(c(seq(3,8,l=30), op$par[1])) # valores para alpha
perfil <- sapply(alpha,
                function(a){
                 op <- optim(coef(rp), ll.alpha, alpha=a, y=cap$nc, X=X,
                             method="BFGS", control=list(fnscale=-1))
                 c(op$value, op$par[1])
                 })

coef <- op$par; vcov <- -solve(op$hessian); llik <- op$value
alp <- coef["alpha"]; sd.alp <- sqrt(vcov["alpha","alpha"])
dev.perf <- 2*(llik-perfil[1,])  # deviance da log-ver perfilhada
dev.quad <- (alp-alpha)^2/sd.alp # deviance da aprox quadrática

require(rootSolve)
qchi <- qchisq(0.95, df=1)
fperf <- approxfun(alpha, dev.perf-qchi)
lim <- uniroot.all(fperf, c(0, 10)) # limites do IC perf
lim2 <- alp+c(-1,1)*1.96*sd.alp     # limites do IC assint

O perfil de log-verossimilhança para \(\alpha\) está representado na Figura 5.6. A aproximação quadrática apresentou intervalos de mesma amplitude daqueles obtidos pelo perfil de verossimilhança, porém com um leve deslocamento para a esquerda. Nenhum dos intervalos contém o valor sob a hipótese nula e portanto os dados apresentam subdispersão. Assim, o número de capulhos por algodão apresenta uma distribuição mais regular que aquela prevista pela distribuição de Poisson.

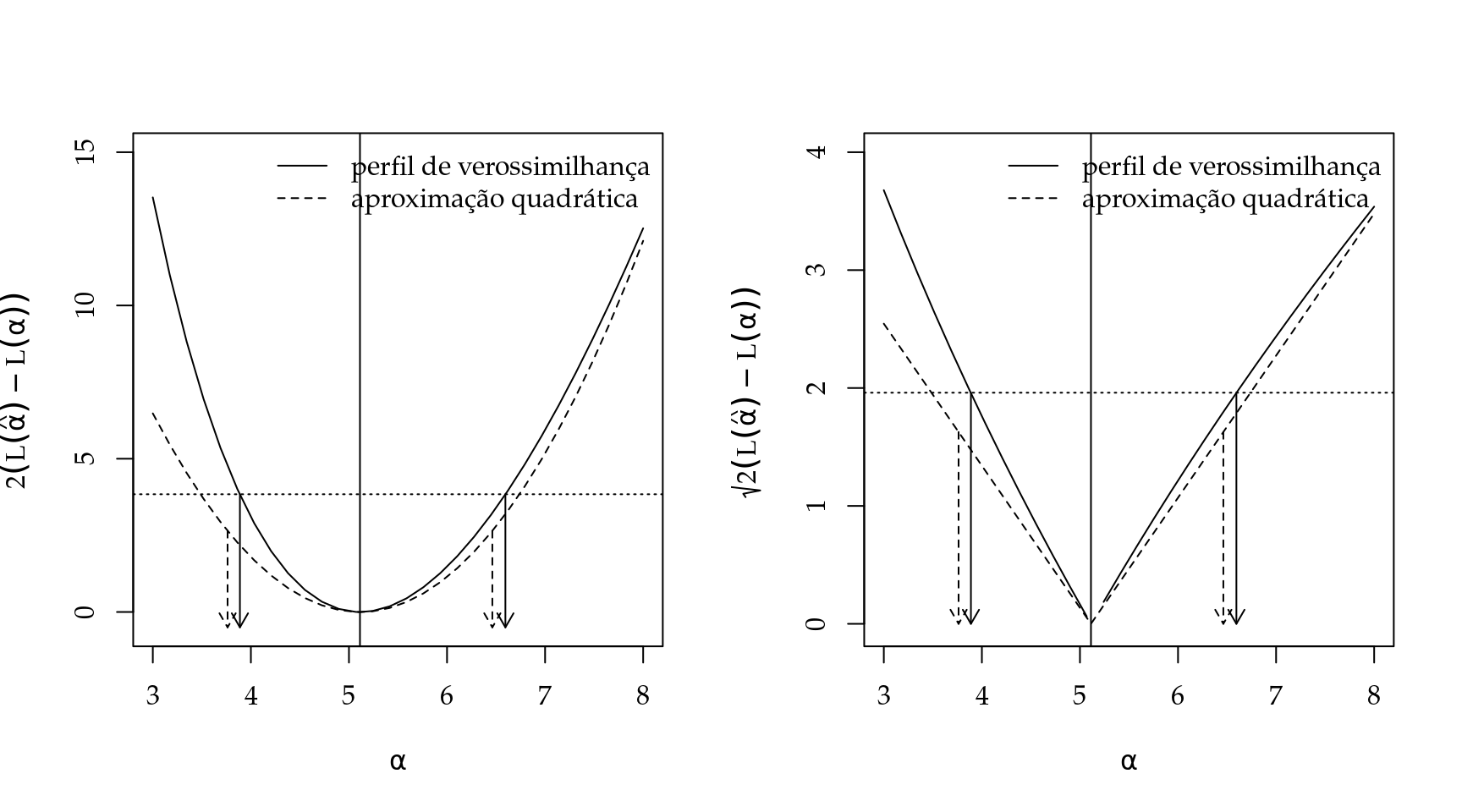
Figura 5.6: Perfil de log-verossimilhança representado pelo valor na diferença na deviance (esq.) e a raíz da diferença na deviance (dir.) para o parâmetro \(\alpha\). Setas indicam os limites do intervalo de confiança.

Os valores esperados para o número de capulhos foram obtidos pela equação (5.3), bem como os limites do intervalo de predição (Figura 5.7).

As estimativas dos parâmetros do modelo indicam que não existe efeito de desfolha no estágio presença de capulhos. No florescimento a desfolha reduz o número de capulhos à taxas decrescentes, o impacto é maior para leves desfolhas e a partir de 70% não há mais considerável redução. Nos demais estágios observa-se uma tolerância à até 30% de desfolha sem prejuízo aos capulhos, acima disso ocorre redução à taxas crescentes.

tabcoef <- data.frame(Estimativas=coef, ErroPadrão=sqrt(diag(vcov)))
tabcoef$zvalor <- with(tabcoef, Estimativas/ErroPadrão)
tabcoef$pvalor <- with(tabcoef, pnorm(abs(zvalor), lower=FALSE)*2)
tabcoef

##                        Estimativas ErroPadrão  zvalor   pvalor
## alpha                       5.1123      0.689  7.4228 1.15e-13
## (Intercept)                 2.2342      0.028 79.7162 0.00e+00
## estvegetativo:des           0.4120      0.228  1.8074 7.07e-02
## estbotao:des                0.2744      0.224  1.2223 2.22e-01
## estflor:des                -1.1822      0.267 -4.4353 9.20e-06
## estmaca:des                 0.3196      0.250  1.2790 2.01e-01
## estcapulho:des              0.0071      0.223  0.0319 9.75e-01
## estvegetativo:I(des^2)     -0.7626      0.258 -2.9538 3.14e-03
## estbotao:I(des^2)          -0.4641      0.250 -1.8533 6.38e-02
## estflor:I(des^2)            0.6453      0.300  2.1489 3.16e-02
## estmaca:I(des^2)           -1.1989      0.297 -4.0380 5.39e-05
## estcapulho:I(des^2)        -0.0186      0.244 -0.0761 9.39e-01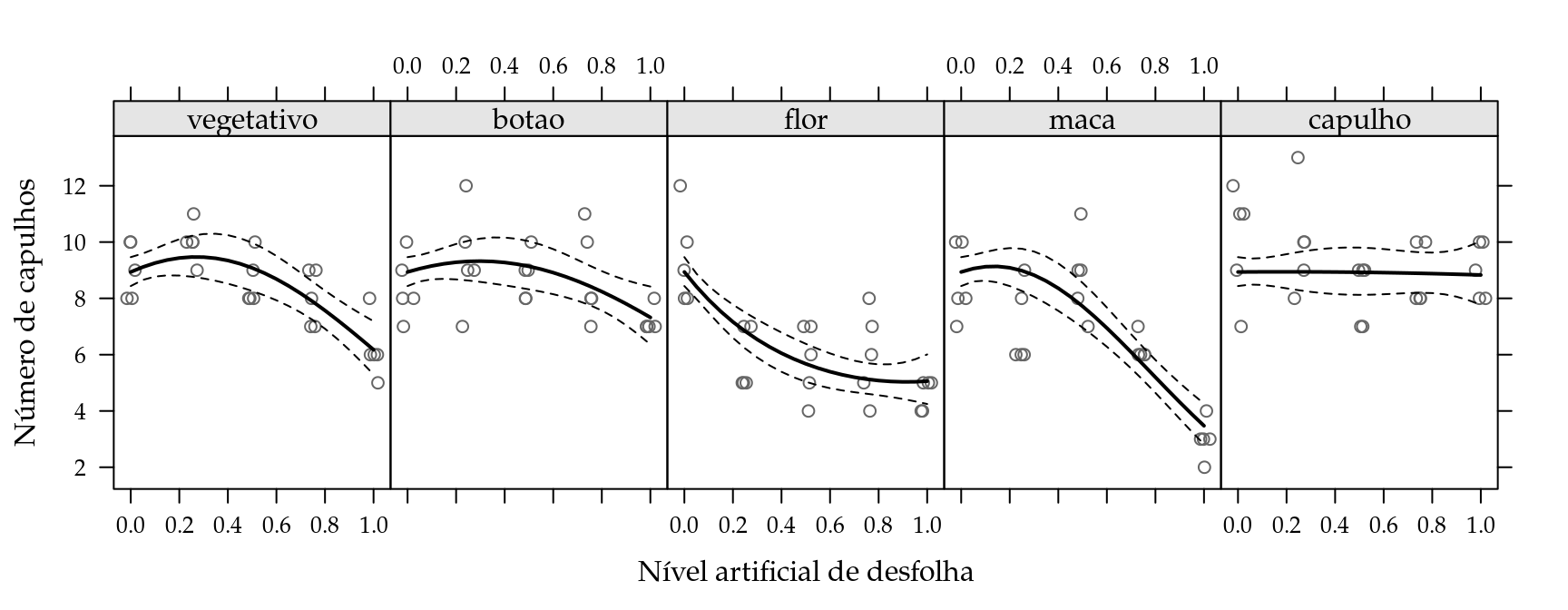

Figura 5.7: Valores observados e preditos acompanhados do intervalo de confiança de 95% para o número de capulhos do algodão em função do nível de desfolha e estágio fenológico.

5.4 Parametrização em modelo não lineares

Um modelo de regressão é não linear quando pelo menos uma derivada do modelo em relação aos parâmetros não for livre dos parâmetros. Em geral, a adoção de modelos de regressão não linear está associado à considerações teóricas sobre a parte mecanística/determinística do fenômeno. Modelos dessa classe são frequentes na física e na química onde os resultados para experimentos simples, como determinar o tempo de queda livre de um objeto e o produto final de uma reação química, podem ser determinados pelo conhecimento das condições experimentais. Por construção, os modelos não lineares possuem parâmetros com significado de forma que o conhecimento desses parâmetros permite uma interpretação fundamentada do fenômeno por meio dos parâmetros que o determinam/governam.

O modelo logístico é um modelo de regressão não linear largamente usado em diversas áreas. Na área biológica é empregado principalmente para descrever o crescimento ou evolução, como crescimento de seres vivos e evolução de doenças. Devido à grande aplicação por diversas áreas, o modelo apresenta diferentes parametrizações, motivadas pela conveniente interpretação que cada uma delas dá ao fenômeno. Entretanto, como já apresentado nos capítulos anteriores, a parametrização de um modelo têm um importante papel com relação a estabilidade numérica do processo de estimação e a qualidade das inferências estatísticas.

De forma simplificada, o modelo logístico tem a seguinte expressão geral

\[\begin{equation} \text{logis}(x, \theta, \beta) = \frac{\theta}{1+f(\exp\{x\},\beta)} \end{equation}\]

em que \(x\) é a variável independente, \(\theta\) é a assíntota do modelo que representa o valor limite da função quando \(x\) tende ao infinito, e \(f(\cdot)\) é uma função do vetor de parâmetros \(\beta\) e do exponencial de \(x\). As reparametrizações desse modelo surgem das diferentes formas da função \(f(\cdot)\). Vamos aqui considerar quatro parametrizações, a saber

• \(f_a(x) = \exp\{(a_1-x)/a_2\}\);

• \(f_b(x) = b_1 \exp\{b_2 x\}\);

• \(f_c(x) = \exp\{c_1+c_2 x\}\);

• \(f_d(x) = (-1+1/d_1)\exp\{-d_2 x\}\).

Em todas essas parametrizações consideramos \(\theta\) conhecido e igual a 1 simplesmente para facilitar as ilustrações dos resultados e superfícies de verossimilhança.
O vetor \(\beta\) com dois elementos representados por letras arábicas. Todas as expressões são reparametrizações de um mesmo modelo. Para ilustrar, considere o modelo \(f_a(\cdot)\) de onde obtemos que

\[ \begin{array}{lll} b_1=\exp\{a_1/a_2\} & c_1=a_1/a_2 & d_1=1/(1+\exp\{a_1/a_2\})\\ b_2=-1/a_2 & c_2=-1/a_2 & d_2=1/a_2. \\ \end{array} \]

Dessa maneira, a partir das estimativas pontuais sob qualquer modelo podemos obter as de qualquer outro aplicando as equações de reparametrização. Este é um fato importante pois podemos ajustar ao dados apenas ao modelo que seja mais adequado para estimação e inferência e também computacionalmente e a partir deste obter estimativas em outras parametrizações que podem ser desejáveis para interpretações práticas.

Para avaliar a inferência sob diferentes parametrizações, faremos o ajuste de cada uma delas à dados de incidência de ferrugem do pessegueiro, causada pelo fungo Tranzshcelia discolor, em função do tempo em plantas da cultivar Chimarrita (figura 5.8). O pomar foi implantado em 2004 em Curitiba (25\(^\circ\), 55’ 10’’ S, 49\(^\circ\) 57’ 26’’ W, 945m), com espaçamento de 1m entre plantas de 2,5m entre linhas. Cada planta foi considerada como uma unidade experimental onde foram avaliadas o número de folhas com presença de ferrugem em relação ao total. Isso foi feito em 6 ramos marcados por planta durante 14 avaliações com intervalo de 10 à 16 dias entre avaliações. Para análise considerou-se a proporção observada de folhas atacadas.

Considerou-se o modelo gaussiano para as observações e a função de log-verossimilhança foi implementada de forma a receber qualquer modelo de regressão não linear (código 5.9). Esta suposição é usual na prática embora, neste contexto, uma resposta binomial poderia ser considerada. As funções em R para os modelos foram criadas e a estimação foi feita pela optim(). Após a estimação foram obtidos os contornos de log-verossimilhança para os pares de parâmetros mostrados na Figura 5.9.

Código 5.9 Função de log-verossimilhança para modelos de regressão não linear.

ll <- function(th, y, x, model){
  ex <- do.call(model, list(x=x, th=th))
  sd <- sqrt(crossprod(y-ex)/length(x))
  ll <- sum(dnorm(y, mean=ex, sd=sd, log=TRUE))
  ll
}

# parametrizações
f.a <- function(x, th){ 1/(1+exp((th[1]-x)/th[2])) }
f.b <- function(x, th){ 1/(1+th[1]*exp(th[2]*x)) }
f.c <- function(x, th){ 1/(1+exp(th[1]+th[2]*x)) }
f.d <- function(x, th){ 1/(1+(-1+1/th[1])*exp(-th[2]*x)) }

# dados
y <- dados$inc2; x <- dados$dia

# lista com valores iniciais e modelo
init.list <- list(A=list(par=c(80,13), model=f.a),
                  B=list(par=c(120,-0.06), model=f.b),
                  C=list(par=c(5,-0.06), model=f.c),
                  D=list(par=c(0.008, 0.065), model=f.d))

# lista com termos fixos durante otmização
fixed.list <- list(fn=ll, x=x, y=y, method="BFGS",
                   control=list(fnscale=-1))

# otimização em série dos modelos
op.all <-
  lapply(init.list,
         function(i){
           op <- do.call(optim, c(i, fixed.list)); op
         })

# estimativas dos parâmetros
pars <- sapply(op.all, "[[", "par"); pars

##         A        B       C       D
## [1,] 73.1 120.0100  4.8159 0.00846
## [2,] 15.2  -0.0655 -0.0658 0.06517

# log-verossimilhança dos modelos
ll0 <- sapply(op.all, "[[", "value"); ll0

##    A    B    C    D 
## 57.1 57.1 57.1 57.1

# contornos de log-verossimilhança
leng <- 100
grid.a <- expand.grid(th1=seq(67,79,l=leng), th2=seq(11,20,l=leng))
grid.a$ll <- apply(grid.a, 1, ll, y=y, x=x, model=f.a)
grid.a$dev <- with(grid.a, -2*(ll-ll0["A"]))

levels <- c(0.05,0.5,0.75,0.9,0.95,0.99)
qchi <- qchisq(levels, df=2)

require(lattice)

contourplot(dev~th1+th2, data=grid.a, at=qchi,
            labels=list(labels=as.character(levels), cex=0.8))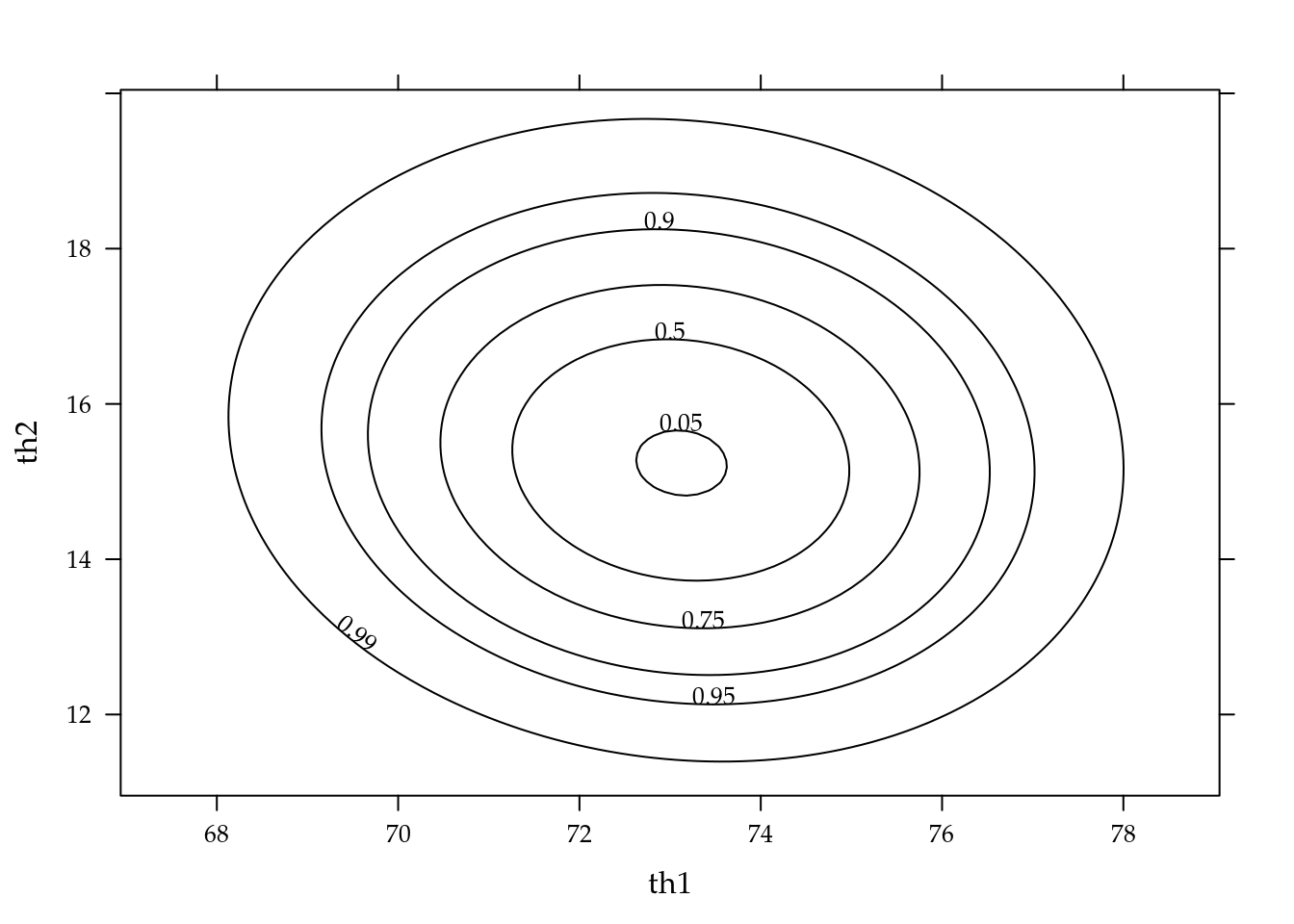

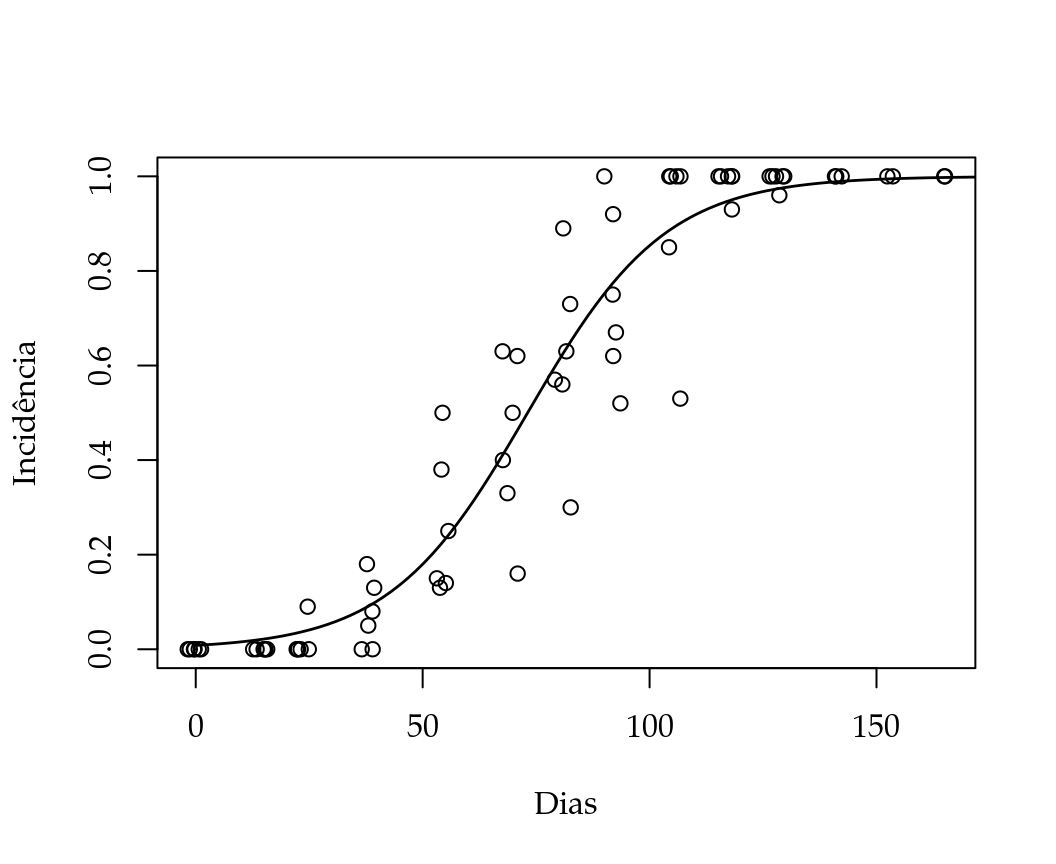
Figura 5.8: Valores observados e ajustados de incidência em função do tempo. As parametrizações são iguais em termos de valores ajustados.

Verifica-se que na parametrização~\(A\) os contornos de deviance são praticamente elípticos com eixos paralelos aos eixos cartesianos. Do ponto de vista de otimização, o procedimentos baseados em avaliação de gradiente tem melhor taxa de convergência quando à função objetivo apresenta simetria e ortogonalidade. Do ponto de vista de inferência estatística, por exemplo na obtenção de intervalos de confiança, a ortogonalidade permite fazer inferência para um parâmetro sem a necessidade de correções considerando a curvatura na direção dos demais parâmetros.

A parametrização \(C\), em comparação com \(A\), apresentou rotação dos eixos do contorno com inclinação negativa e uma leve assimetria dos contornos. A rotação deve-se ao fato de que as funções de reparametrização entre \(A\) e \(C\) são praticamente lineares e a assimetria devido a uma delas ser um quociente. As parametrizações \(B\) e \(D\) apresentaram forte desvio da forma elíptica com contornos em formato de “banana.” Dentre esses últimos, o modelo \(B\) parece ser o mais susceptível e pode apresentar problemas numéricos pois apresenta assimetria mais acentuada do que o modelo \(D\). Dessa forma, as parametrizações em termos de conveniência para estimação e inferência estatística seguem a ordem de preferência: \(A\), \(C\), \(D\) e \(B\). Vale relembrar que tanto as estimativas pontuais quanto intervalares do modelo em uma parametrização podem levar aos seus equivalentes em outra parametrização pelo princípio da invariância do estimador de máxima verossimilhança.

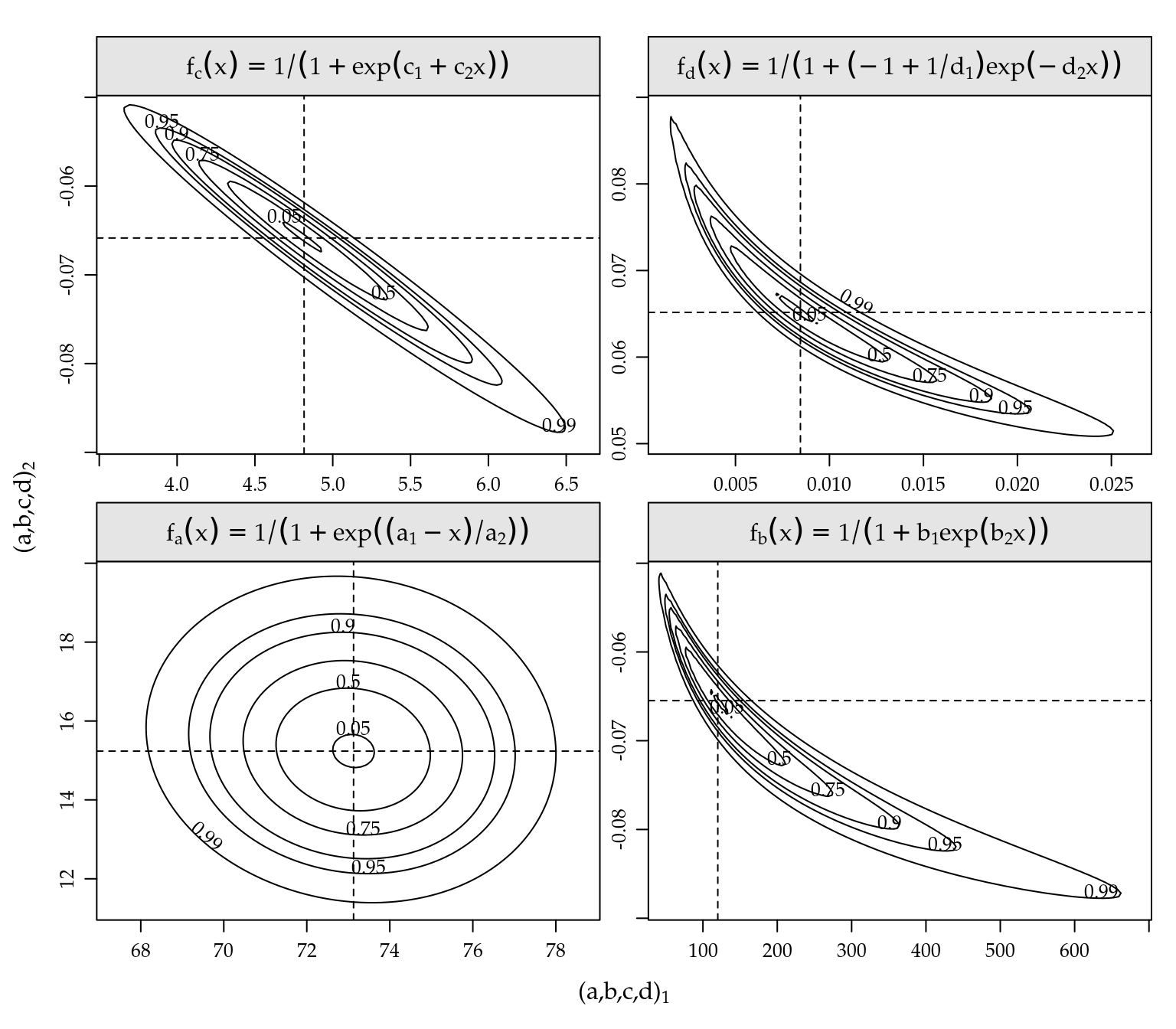
Figura 5.9: Contornos de deviance para os parâmetros do modelo logístico em cada uma das parametrizações.

5.5 Processo Pontual

Um processo pontual é um tipo de processo estocástico no qual cada realização consiste de um conjunto contável de posições \(x_i\) registradas em uma região. Os pontos de ocorrência são chamados de eventos. As posições são registradas em tempos e/ou localizações no espaço, embora possam ser anotadas em outros espaços. Tipicamente o objetivo é verificar se há algum padrão que possa ser associado à ocorrência dos pontos. Denotamos por \(N(A)\) o número de eventos que ocorre em uma região, \[ N(A) = \#(x_i \in A) . \]

O processo é estacionário se, para qualquer inteiro \(k\) e regiões \(A_i : i = 1, \dots, k\), a distribuição conjunta de \(N(A_1), \dots, N(A_k)\) é invariante a translações por uma quantidade arbitrária \(x\).

Um processo pontual pode ser caracterizado por sua função de intensidade \(\lambda(x)\) que está associada à
probabilidade de ocorrência de eventos na região. As seguintes definições são análogas aos conceitos de média e (co)variância para processos com valores nos reais e caracterizam a ocorrência e interação dos eventos em um processo pontual. Denote por \(dx\) uma pequena região contendo o ponto \(x\).

Definição 5.1 (Função de intensidade (de primeira ordem).) \[ \lambda({x}) = \lim_{|d{x}| \to 0} \left\{\frac{E[N(d{x})]}{|d{x}|} \right\} \]

Definição 5.2 (Função de intensidade de segunda ordem.) \[ \lambda_2({x}_i,{x}_j) = \lim_{\stackrel{\scriptstyle |d{x}_i| \to 0}{\scriptstyle |d{x}_j | \to 0}} \left\{\frac{E[N(d{x}_i)N(d{x}_j)]}{|d{x}_i| |d{x}_i|}\right\} \]

Definição 5.3 (Densidade de covariância.) \[ \gamma({x}_i, {x}_j) = \lambda_2({x}_i, {x}_j) - \lambda({x}_i) \lambda ({x}_j). \]

Se o processo pontual é estacionário (e isotrópico no caso de processos espaciais) segue que:

1. \(\lambda({x}) = E[N(d{x})]/|d{x}| \equiv \lambda = E[N(A)]/|A|\), (constante, em todo \(A\))

2. \(\lambda_2({x}_i,{x}_j) \equiv \lambda_2(\|{x}_i-{x}_j\|)\) (depende apenas da distância \(s=\|{x}_i-{x}_j\|\))

3. \(\gamma({x}_i,{x}_j) \equiv \gamma(s) = \lambda_2(s) - \lambda^2\).

Uma classe particular de processos pontuais são os processos de Poisson, nos quais os eventos
ocorrem de maneira independente uns dos outros, ou seja, a ocorrência de um evento em uma localização não modifica a probabilidade de ocorrência de eventos em sua vizinhança.

Definição 5.4 (Processo de Poisson) Seja \(\lambda({x})\) uma função não negativa, a intensidade de um processo pontual. Então:

1. O número de eventos, \(N(A)\), em qualquer região \(A\) d segue uma distribuição Poisson com média \[ {\rm E}[N(A)] = \int_A \lambda({x}) d{x} \]

2. dado \(N(A)=n\), as localizações dos \(n\) eventos em \(A\) formam uma amostra aleatória independente da distribuição em \(A\) com função de densidade de probabilidade proporcional a \(\lambda({x})\).

Se sob as condições anteriores \(\lambda({x})=\lambda\), para todo \({x}\), o processo é dito ser um processo de Poisson homogêneo (PPH) e corresponde a total aleatoriedade. Neste caso, \(\lambda\) é interpretado como o número esperado de eventos por unidade de tamanho da região, ou seja, o número esperado de eventos na região é \(\lambda ||A||\) em que \(||A||\) é a dimensão da região.

De forma mais geral se \(\lambda({x})\) não é contante sobre a área, o processo é dito um processo de Poisson não-homogêneo (PPI) e o número esperado de eventos em uma região \(A_i\) é \(\int_{A_i} \lambda({x}) d({x})\).

Dentre as propriedades dos processos de Poisson estão:

1. Os números de eventos \(N(A)\) e \(N(B)\) tomados em duas regiões disjuntas são variáveis aleatórias independentes

2. \({\rm Var}\{N(A)\}/{\rm E}[N(A)] = 1\), em todo \(A\)

3. para o processo de Poisson homogêneo, a função de distribuição da distância \(u\) de um ponto arbitrário ao evento mais próximo é \[ F(u) = 1 - \exp(-\lambda \pi u^2): u>0 \]

Em nosso exemplo vamos considerar apenas processos em uma dimensão, por exemplo em um intervalo de tempo,
que sejam Poisson homogêneo ou não-homogêneo. Para este último consideramos uma função de densidade \(\lambda(t)\) que seja apenas função do tempo. O objetivo é ilustrar como escrever a função de verossimilhança do processo e obter as estimativas.

Inicialmente vamos definir funções para simular realizações dos processos. Para o processo de Poisson homogêneo uma simulação pode ser obtida com os seguintes passos.

1. definir o região para simulação;

2. encontrar o número esperado de eventos na região \(\lambda \Delta_t\);

3. simular o número \(N\) de eventos de uma Poisson com média \(\lambda \Delta_t\);

4. obter as localizações dos eventos simulando de uma distribuição uniforme sobre a região.1.

Estes passos estão implementados no código 5.10 e a chamada da função simula um processo com \(\lambda=0,8\) no intervalo \((0,100)\) e portanto com o número esperado de pontos igual a 80.

Código 5.10 Função para simular de um PPH em uma dimensão.

simPPH1 <- function(lambda, min, max){
    Nexp <- lambda * (max - min)
    N <- rpois(1, lambda=Nexp)
    return(runif(N, min = min, max = max))
}

set.seed(56)
pp1 <- simPPH1(0.8, 0, 100)
(n1 <- length(pp1))

## [1] 77

Uma outra maneira de simular de um PPH implementada no código 5.11 é usar o fato de que o intervalo entre eventos possui distribuição exponencial. Desta forma, simula-se sequencialmente os tempos dos eventos e acumulam-se os valores até chegar ao limite do intervalo de tempo desejado. Esta forma pode parecer um pouco mais extensa mas a estratégia de simulações sequenciais é útil por poder ser mais facilmente expandida para outros tipos de processos.

Código 5.11 Função para simular de um PPH em uma dimensão.

simPPH2 <- function(lambda, min, max){
  x <- min
  while(sum(x) <= max)
  x <- c(x, rexp(1, rate=lambda))
  x <- x[-c(1, length(x))]
  return(cumsum(x))  
}

Na figura 5.10 são mostradas duas simulações uma com cada uma das funções apresentadas. Sob a suposição de PPH a densidade acumulada dos valores das posições dos eventos é a de uma distribuição uniforme. Os gráficos na parte de baixo da figura mostram as distribuições acumuladas e empíricas.

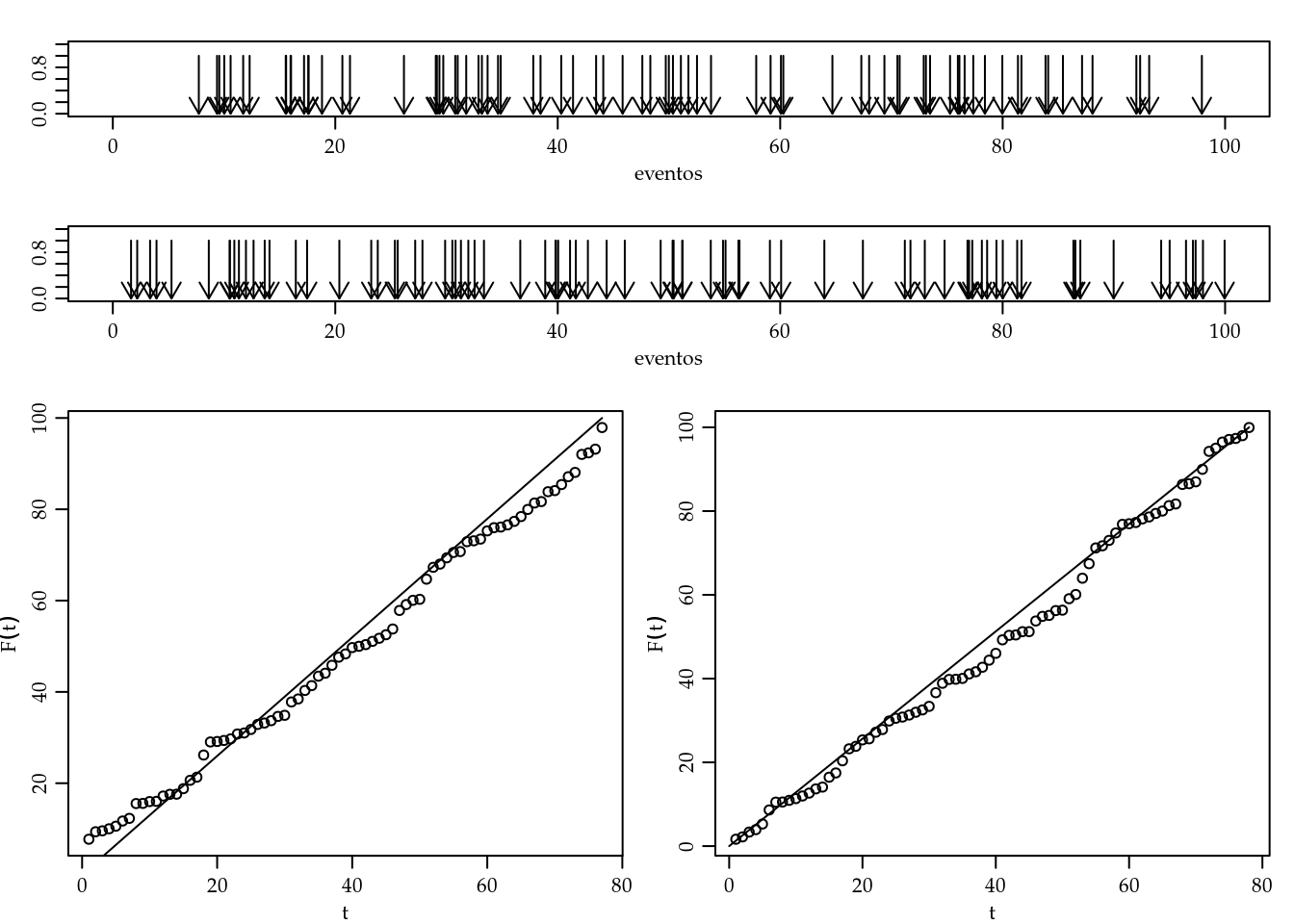
Figura 5.10: Simulações do PPH com as funções apresentadas (superiores) e densidades acumuladas.

Passamos agora de um processo de Poisson não-homogêneo a considerar um caso simples com \({x} = t\) e a função de intensidade \(\lambda(t) = \exp(\beta_0 + \beta_1 t)\). Este poderia ser um caso no qual estaríamos interessados em avaliar se a taxa de eventos está aumentando com o passar do tempo.

Código 5.12 Função de intensidade de um PPI simples.

lambda.x <- function(x, par, log=FALSE){
    eta <- par[1] + par[2] * x
    if(log) return(eta) else return(exp(eta))
}

Para simular de um PPI podemos usar e estratégia de simulação por rejeição que ilustramos no código 5.13. Para isto simulamos de um processo mais simples (PPH) e submetemos cada evento simulado a uma regra adequada de aceitação/rejeição de tal forma que os eventos aceitos constituem uma simulação do PPI desejado. Os passos são:

1. encontrar o valor \({\rm max}[\lambda(t)]\), o máximo de \(\lambda(t)\) na região,
2. simular de um PPH na região com \(\lambda = {\rm max}[\lambda(t)]\),
3. aceitar cada evento simulado com probabilidade \(P[{\rm aceitar}] = \lambda(t_i)/{\rm max}[\lambda(t)]\).

O último passo pode ser descrito como: simular uniformemente no retângulo definido pela região \(\times\) \({\rm max}[\lambda(t)]\) e selecionar como eventos as abcissas dos pontos para os quais a ordenada é menor do que \(\lambda(x)\).
No código, adotamos a solução mais geral de maximizar \(\lambda(t)\) numericamente, embora para casos em que este valor pode ser encontrado analiticamente, o código pode ser simplificado. No exemplo temos \({\rm max}[\lambda(t)] = \lambda(100) = \exp\{-1 + 0,015 \cdot 100\} \approx 2\).

Código 5.13 Função para simular de um PPI simples.

simPPI <- function(par, min, max){
  nHPP <- round(optimize(lambda.x, c(min, max), par=par, 
                maximum=TRUE)$objective * (max - min))
  X <- runif(nHPP, min, max)
  p.aceita <- lambda.x(X, par)*(max - min)/nHPP
  ppI <- sort(X[runif(nHPP) <= p.aceita])
  attributes(ppI) <- list(simulados=nHPP,aceitos=length(ppI),taxa=length(ppI)/nHPP)
  return(ppI)
}

A seguir geramos uma realização processo com \(\beta_0=-1\) e \(\beta_0=0,015\) em um intervalo \((0, 100)\), portanto com um número esperado de pontos de 85. Na figura 5.11 a simulação a esquerda mostra claramente o aumento da densidade de pontos com o passar do tempo, o gráfico da direita mostra claramente que o padrão é incompatível com um PPH.

set.seed(5665)
pp3 <- simPPI(c(-1, 0.015), 0, 100)
unlist(attributes(pp3))

## simulados   aceitos      taxa 
##   165.000    88.000     0.533

(n3 <- length(pp3))

## [1] 88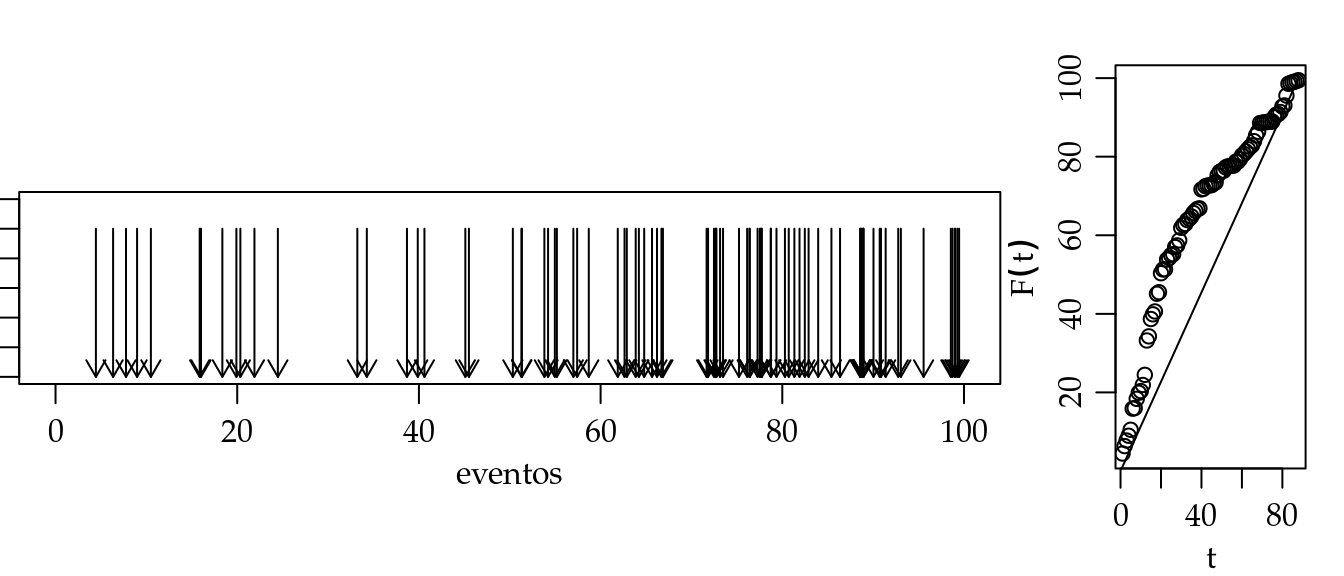

Figura 5.11: Simulação de um PPI (esquerda) e densidade acumuladas (direita).

A função de verossimilhança de um processo pontual é obtida considerando as densidades das duas variáveis aleatórias observadas, o número de eventos \(N\) e as localizações \(\{t\}\). Portanto, para um conjuntos de valores de parâmetros de um modelo considerado, o valor da verossimilhança é dada pela probabilidade de observar o número de eventos de fato obtido no conjunto de localizações observadas. Para um processo de Poisson \(N \sim P[\int_A \lambda(t) dt]\) e para cada ponto pode ser atribuído \(P[\{t_i\}] = \lambda(t_i)/\int_A \lambda(t) dt\).

\[\begin{align*} L(\theta) &= \frac{e^{-(\int_A \lambda(t) dt)} (\int_A \lambda(t) dt)^N}{N!} \prod_{i=1}^N \frac{\lambda(t_i)}{\int_A \lambda(t) dt} \propto e^{-(\int_A \lambda(t) dt)} \; \prod_{i=1}^N \lambda(t_i) \\ l(\theta) &\propto \sum_{i=1}^N \log(\lambda(t_i)) - \int_A \lambda(t) dt \end{align*}\]

Para o PPH o estimador de máxima verossimilhança é intuitivo, tem forma fechada e é dado pela taxa de eventos, ou seja, pelo número de pontos observados dividido pela dimensão \(||A||\) da região e a verossimilhança maximizada assume uma forma simples.

\[\begin{align*} \hat{\lambda} &= \frac{N(A)}{||A||} = \frac{\#({x}_i \in A)}{||A||} \\ l(\hat{\lambda}) &\propto N \log(\hat{\lambda}) - \hat{\lambda} ||A|| \end{align*}\]

Para os dados da primeira simulação de um HPP temos:

(lambda1.est <- n1/(100-0))

## [1] 0.77

(lambda1.ll <- n1 * log(lambda1.est) - lambda1.est * (100-0))

## [1] -97.1

Para um PPI a obtenção do estimador de máxima verossimilhança vai depender da forma de \(\lambda(x)\). Para o modelo usado anteriormente para simular de um PPI temos que \[ l(\beta_0, \beta_1) \propto \sum_{i=1}^N \log(\beta_0 + \beta_1 t_i ) - \int_A \beta_0 + \beta_1 t \; dt . \] Embora em certos casos seja possível encontrar expressões fechadas para os estimadores,
vamos considerar o caso mais geral no qual utilizamos maximização numérica. A expressão da verossimilhança do PPI considerado aqui é definida no código 5.14. Neste código \(\lambda(x)\) é integrado numericamente, embora neste exemplo a expressão analítica da integral é facilmente obtida.
Se ocorrerem instabilidades numéricas pode-se transformar os valores das localizações dos pontos para o intervalo \((0,1)\). Neste exemplo isto não foi necessário, mas em outras casos não reportados aqui, com diferentes valores dos parâmetros foi fundamental para obtenção das estimativas corretas.

Código 5.14 Função de log-verossimilhança para o PPI simples.

nlikIPP <- function(par, PP, min, max){
  intLx <- integrate(lambda.x, low=0, upp=100, par=par)$value   
## Se necessário reescalonar usar:
##  PP <- (PP - min)/(max-min)
##  intLx <- integrate(lambda.x, low=0, upp=1, par=par)$value   
  slxi <- sum(lambda.x(x=PP, par = par, log=T))
  return(-(slxi - intLx))
}

As estimativas para a simulação do PPI são obtidas a seguir. Caso seja usado o reescalonamento de coordenadas é necessário transformar os valores dos parâmetros adequadamente. O gráfico à esquerda da Figura 5.12 mostra a superfície de verossimilhança para os dados simulados. Os contornos delimitam, de dentro para fora, regiões de confiança de 5, 10, 30, 50, 70, 90, 95 e 99%. As linhas sólidas indicam o corte para obtenção das verossimilhanças perfilhadas e
as pontilhadas das condicionadas no MLE, para cada parâmetro. Os demais gráficos mostram as verossimilhanças individuais perfilhadas e condicionada no MLE, ficando claro que a última subestima dramaticamente a variabilidade por desconsiderar a não ortogonalidade.

(ppI.est <- optim(c(0,0.01), nlikIPP, PP = pp3, min=0, max=100)[1:2])

## $par
## [1] -1.2665  0.0197
## 
## $value
## [1] 86.3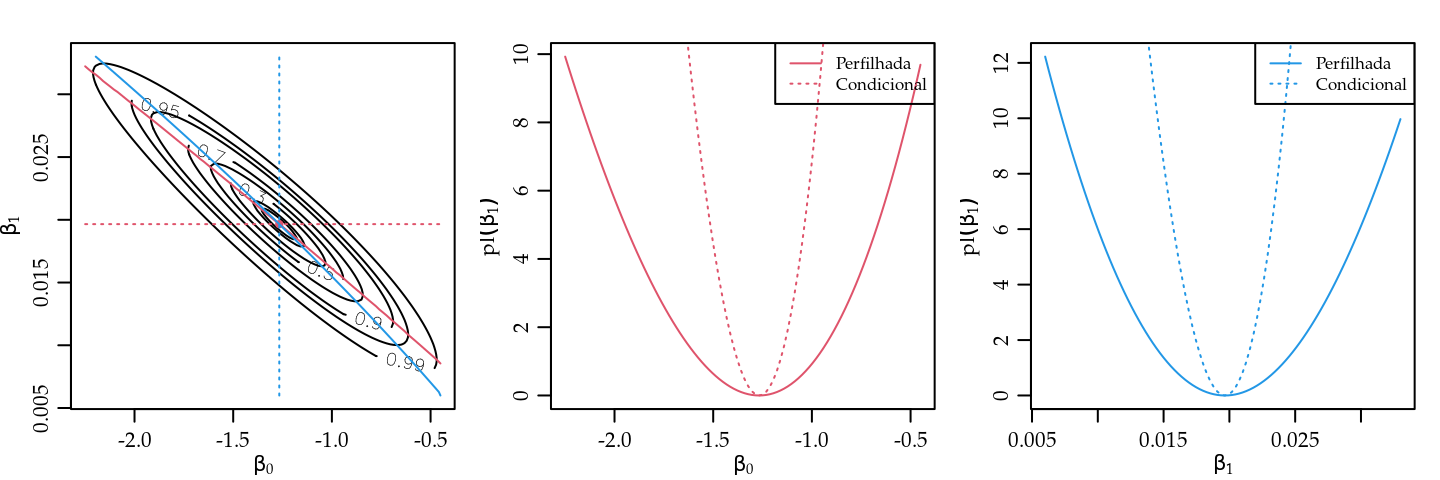

Figura 5.12: Superfície de deviance (esquerda), e perfil de deviances para os parâmetros \(\beta_0\) (centro) e \(\beta_1\) (direita) para dados de um PPI.

Possíveis extensões incluem inferências usuais como intervalos de confiança e perfis de verossimilhança. Um resultado de particular interesse é testar se o padrão é homogêneo. Podemos comparar as verossimilhanças maximizadas do PPH e PPI para o mesmo conjunto de dados, por exemplo, para fazer um teste da razão de verossimilhança a fim de determinar se o modelo com taxa não contante é mais compatível com os dados.

## PPH
(lambda3.est <- n3/(100-0))

## [1] 0.88

(lambda3.ll <- n3 * log(lambda3.est) - lambda3.est * (100-0))

## [1] -99.2

-ppI.est$value   ## para PPI

## [1] -86.3

-2*(lambda3.ll - (-ppI.est$value))

## [1] 25.9

Os modelos descritos aqui são básicos e podem ser estendidos de diversas formas. A função \(\lambda(t)\) pode ter uma forma mais complexa como, por exemplo, um polinômio ou um spline em \(t\). A função intensidade pode ser função de uma outra variável (temperatura, altitude, etc) que não a posição \(t\). Em problemas espaciais no plano as posições dos eventos são dadas pelas coordenadas e a função de intensidade pode ser de duas variáveis \(\lambda(x,y)\) e a integração é bidimensional. De forma mais genérica, a intensidade pode ser função de múltiplas coordenadas e/ou variáveis auxiliares o que torna o problema computacionalmente mais complexo por exigir integrações múltiplas. Uma extensão possível é especificar uma função de intensidade que seja aleatória, o que torna o procedimento de inferência bem mais desafiador. Diversos outros processos pontuais que não assumem independência entre eventos são discutidos na literatura. Tais processos podem acomodar interações, tais como atrações ou repulsões, entre eventos e estão além incluem na classe de processos de Poisson.

Como referência inicial para processos pontuais espaciais citamos Peter J. Diggle (2003). Há diversos pacotes no R implementando métodos para processos pontuais e dentre eles citamos o pacote spatstat Baddeley and Turner (2005) que além de funções para simular e analisar diversos tipos de processos pontuais possui uma extensa e detalhada documentação.