Chapter 1 Introdução
A abordagem estatística para análise e resumo de informações contidas em um conjunto de dados, consiste na suposição de que existe um mecanismo estocástico gerador do processo em análise. Este mecanismo é descrito através de um modelo probabilístico, representado por uma distribuição de probabilidade. Em situações reais a verdadeira distribuição de probabilidade geradora do processo é desconhecida, sendo assim, distribuições de probabilidade adequadas devem ser escolhidas de acordo com o tipo de fenômeno em análise. Por exemplo, se o fenômeno em estudo consiste em medir uma característica numérica de um grupo de indivíduos em uma escala contínua, distribuições com este suporte devem ser escolhidas. O suporte de uma distribuição de probabilidade informa qual o domínio da função, ou seja, quais são os valores que a variável aleatória pode assumir. Considere o caso da distribuição Gaussiana, o suporte é a reta real, no caso da distribuição gama o suporte é apenas os reais positivos. Um cuidado adicional deve ser dado quando a variável de interesse é discreta, por exemplo contagens, onde é comum atribuir uma distribuição de Poisson que tem suporte nos naturais positivos.
Em quase todos os problemas de modelagem estatística não existe uma única distribuição de probabilidade que pode representar o fenômeno. Porém, na maioria das situações assume-se que a distribuição de probabilidade geradora do processo é conhecida, com exceção dos valores de um ou mais parâmetros que a indexam. Por exemplo, considere que o tempo de vida de um tipo de componente eletrônico tem distribuição exponencial com parâmetro \(\lambda\), mas o valor exato de \(\lambda\) é desconhecido. Se o tempo de vida de vários componentes de mesmo tipo são observados, baseado nestas observações e qualquer outra fonte relevante de informação que esteja disponível, é possível fazer inferência sobre o valor desconhecido do parâmetro \(\lambda\). O processo de inferência consiste em encontrar um valor mais plausível para \(\lambda\), bem como, informar um intervalo para o qual acredita-se conter o verdadeiro valor de \(\lambda\), além de decidir ou opinar se \(\lambda\) é igual, maior ou menor que algum valor previamente especificado. Em alguns problemas há ainda interesse em fazer previsões sobre possíveis valores do processo, por exemplo, em outros tempos ou locais.
Em implementações computacionais para inferência estatística, deve-se sempre estar atento ao espaço paramétrico \((\Theta)\) de um modelo probabilístico. No caso do tempo de vida de componentes eletrônicos, assumindo que a distribuição exponencial é adequada e está sendo indexada pelo parâmetro \(\lambda\), de acordo com a construção do modelo exponencial, tem-se que o espaço paramétrico de \(\lambda\) é dado pelo conjunto dos reais positivos. Em um modelo gaussiano, com média \(\mu\) e variância \(\sigma^2\), o espaço paramétrico é \(\Re \times \Re_{+}\) ou seja, todo o conjunto dos reais para média \(\mu\) enquanto que para \(\sigma^2\) o espaço paramétrico restringe-se aos reais positivos. Outro caso comum são modelos em que o parâmetro representa alguma proporção \(p\) e tem como espaço paramétrico o intervalo \([0,1]\). Estas restrições precisam ser levadas em consideração no processo de inferência e são de fundamental importância para o sucesso de muitos algoritmos de maximização numérica. Não raramente nas implementações computacionais são feitas reparametrizações com novos parâmetros para os quais os valores são projetados na reta real, com resultados transformados de volta ao espaço original. Por exemplo pode-se adotar \(\psi = \log{\sigma}\) para variância do modelo normal e \(\psi = \log{p/(1-p)}\) para a proporção de sucesso em um experimento binomial.
Partindo destes conceitos, um fenômeno aleatório ou estocástico é descrito minimamente por uma distribuição de probabilidade, que por sua vez é indexada por seus parâmetros e respectivos campos de variação espaço paramétrico, além do campo de variação da própria variável aleatória que deve ser compatível com o suporte da distribuição atribuída ao fenômeno. Por exemplo, não é correto atribuir uma distribuição de Poisson para a altura (medida contínua) de trabalhadores, uma vez que o campo de variação da variável de interesse (resposta) não é compatível com o suporte da distribuição de probabilidade.
Considere o caso onde deseja-se fazer uma pesquisa a respeito da intenção de voto em um plebiscito. Suponha que \(n\) eleitores selecionados aleatoriamente são questionados sobre a sua intenção em votar a favor \((1)\) ou contra \((0)\) uma determinada mudança na legislação. Deseja-se estimar a proporção \(\theta\) de eleitores favoráveis à mudança. Assume-se que o modelo Bernoulli seja adequado para a intenção de voto de cada eleitor e portanto o número de favoráveis em uma amostra aleatória de \(n\) eleitores tem distribuição binomial \({\rm B}(n, \theta)\). Este modelo tem como possíveis respostas para cada indivíduo da amostra os valores \(0\) e \(1\) e como parâmetro indexador \(\theta\) que representa a proporção de favoráveis e tem o intervalo unitário como seu espaço paramétrico. Com este conjunto de suposições e conhecimentos a respeito do modelo probabilístico, tem-se total condições de fazer inferência sobre o parâmetro \(\theta\) a partir dos dados de uma amostra.
A Figura 1.1(A) representa a região definida pelo modelo para uma amostra aleatória de tamanho \(100\). A superfície é obtida calculando-se os valores das probabilidades de se observar \(y\) favoráveis em uma amostra para cada um dos possíveis valores do parâmetro. Para visualização omitimos os valores próximos às bordas \([0,1]\). Um corte da superfície de probabilidades em um particular valor do parâmetro fornece uma distribuição de probabilidades para as possíveis respostas como ilustrado na 1.1(B) para \(\theta=0,65\). Um corte para um valor de \(y=60\), que poderia ser o obtido em uma determinada amostra, fornece a função de verossimilhança denotada por \(L(\theta|y)\) que é apresentada na Figura 1.1(C). Tal função fornece uma medida de proximidade entre cada possível valor do parâmetro e a amostra observada.
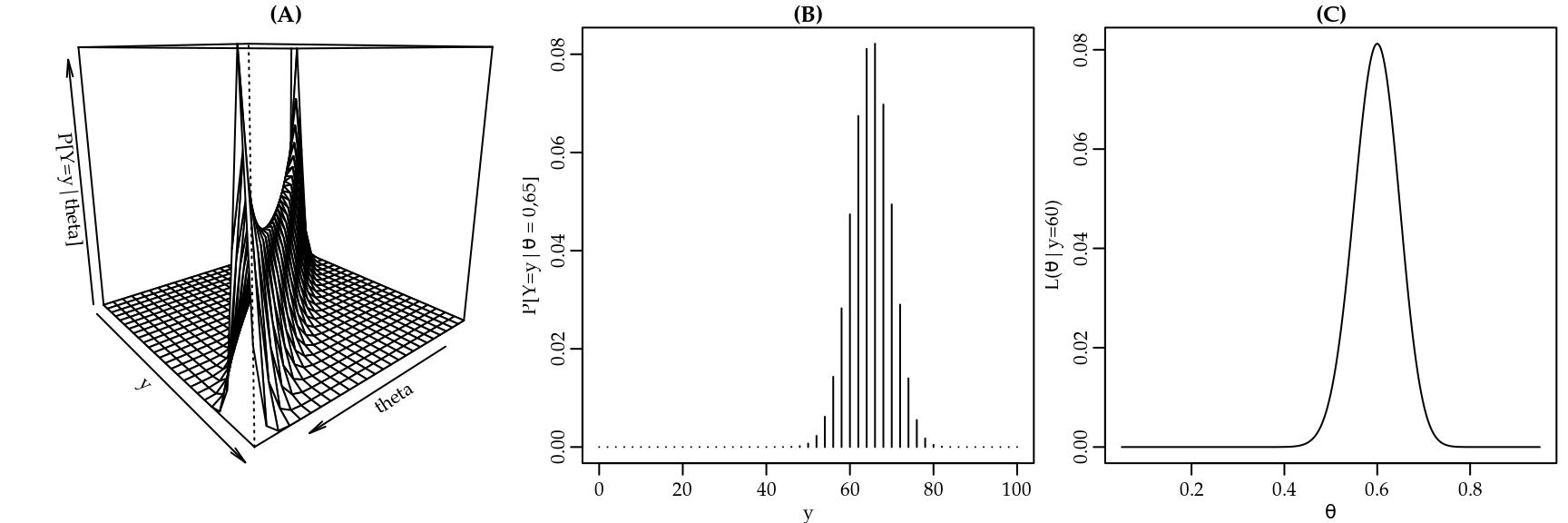
Figura 1.1: Superfície de probabilidades (esquerda), distribuição de probabilidades (centro) e função de verossimilhança (direita) para um modelo binomial.
Em outras palavras, no gráfico da função de verossimilhança \(L(\theta|y)\), a ordenada de cada ponto da curva é dada pela probabilidade do valor \(y\) observado na amostra, ter sido gerado por cada um dos possíveis valores de \(\theta\). Desta forma é intuitivo pensar que a melhor estimativa para o parâmetro, baseada na amostra, é o valor do parâmetro que tem maior probabilidade de gerar o resultado visto na amostra, portanto o valor que maximiza a função de verossimilhança. Isto define o estimador de máxima verossimilhança \(\hat{\theta}\). Também é intuitivo pensar que podemos definir uma “faixa” de valores que possuem uma probabilidade “não muito distante e aceitável” da máxima probabilidade de gerar o resultado visto na amostra. Tal faixa define um estimador por intervalo com valores inferior e superior \((\hat{\theta}_I, \hat{\theta}_S)\) que delimitam uma região no espaço paramétrico que possui valores de verossimilhança que não estejam abaixo de um percentual pré-definido do máximo possível valor da verossimilhança. Finalmente, pode-se verificar se um determinado valor de interesse, tal como \(\theta_0 = 0,5\) no exemplo considerado, é compatível com a amostra comparando-se sua verossimilhança com a máxima possível. Este último caso permite definir um teste de hipótese de interesse para guiar uma tomada de decisão. Na Figura 1.2 redesenhamos o gráfico da função de verossimilhança agora com a escala vertical com valores relativos ao máximo valor e os elementos no gráfico ilustram os três objetivos centrais da inferência estatística.
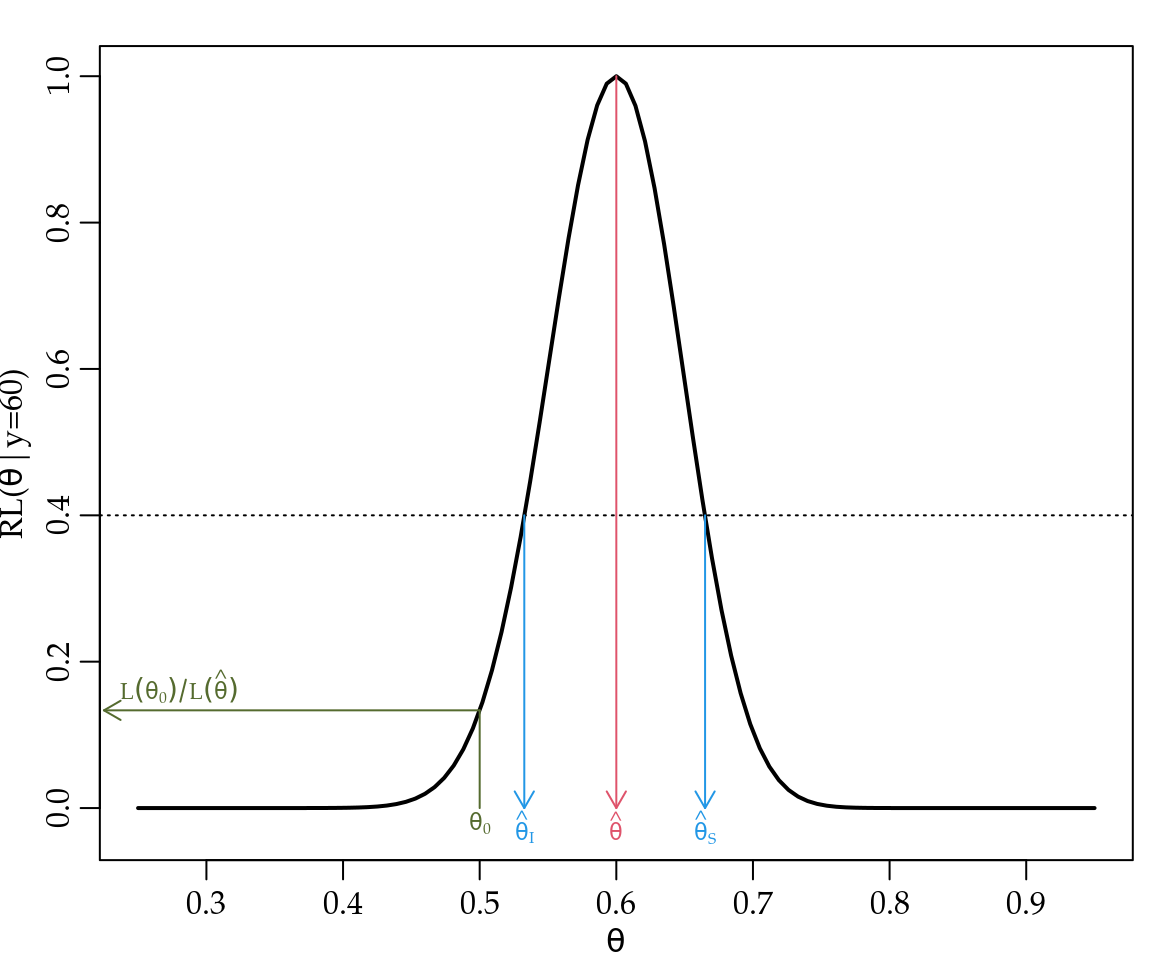
Figura 1.2: Visualização da estimativa de máxima verossimilhança, estimativa intervalar e valor correspondente a uma hipótese na função de verossimilhança relativa (RL) para o modelo binomial.
Neste texto será dada ênfase na inferência baseada na verossimilhança, que fornece estimadores e procedimentos com propriedades desejáveis para os parâmetros desconhecidos de um modelo probabilístico. A função de verossimilhança fornece todos os elementos necessários para a obtenção de estimativas pontuais e intervalares, além da construção de testes de hipóteses. Toda a metodologia será descrita através de exemplos abordando diversos aspectos teóricos, com ênfase na implementação computacional para estimação de parâmetros desconhecidos cobrindo desde modelos simples até modelos altamente estruturados. A abordagem de inferência pela verossimilhança não é, entretanto, a solução de todo e qualquer problema, podendo tornar-se intratável analítica e/ou computacionalmente em certos modelos. Entretanto, os princípios permanecem válidos e diversos procedimentos estendem, aproximam ou substituem a verossimilhança quando necessário. Tais extensões estão fora do escopo deste texto que concentra-se na obtenção da verossimilhança com ênfase em procedimento numéricos.Nossa intenção é reforçar a intuição para aspectos fundamentais e básicos de inferência.
Exercícios
- Para cada uma das distribuições de probabilidade abaixo escreva a
função de probabilidade ou densidade probabilidade, identifique
o suporte, a esperança, a variância, os parâmetros e o espaço paramétrico.
- Distribuição Poisson de parâmetro \(\lambda\).
- Distribuição binomial de parâmetros \(n\) e \(p\).
- Distribuição exponencial de parâmetro \(\lambda\).
- Distribuição normal de parâmetros \(\mu\) e \(\sigma^2\).
- Distribuição gama de parâmetros \(\alpha\) e \(\beta\).
- Distribuição uniforme de parâmetros \(a\) e \(b\).
- Distribuição binomial negativa de parâmetros \(\mu\) e \(\phi\).
- Distribuição log-normal de parâmetros \(\mu\) e \(\sigma^2\).
- Distribuição inversa Gaussiana de parâmetros \(\mu\) e \(\sigma^2\).
- Distribuição Tweeedie de parâmetros \(\mu\), \(\phi\) e \(p\).
- Para cada uma das situações abaixo proponha uma distribuição de probabilidade
adequada e justifique sua escolha baseado em aspectos do fenômeno aleatório e
características da distribuição. Descreva quais aspectos da inferência estatística podem estar associados com cada uma das situações mencionadas.
- Itens em uma linha de produção são classificados quanto a sua adequação aos padrões de produção. Apenas as condições conforme ou não-conforme são possíveis.
- Uma pesquisa de mercado visa identificar o potencial de um novo negócio em uma cidade. Para isto um questionário com perguntas em uma escala likert de cinco níveis foi construído e aplicado a uma amostra de tamanho \(n\) da população de interesse.
- Número de carros que chegam a um caixa automático de um banco durante um período de uma hora nas manhãs de fins de semana.
- Ocorrência de defeitos relevantes em uma rodovia um mês após sua construção.
- Medidas antropométricas (peso e altura) são tomadas em crianças do nono ano de escolas públicas brasileiras. Deseja-se caracterizar tais medidas para auxiliar na construção de equipamentos escolares de tamanho adequado.
- Deseja-se estudar a distribuição do número de horas que um equipamento eletrônico funciona antes de apresentar defeitos com o objetivo de estabelecer um prazo razoável de garantia.
- Número de quilômetros rodados que um novo pneu é capaz de rodar antes de apresentar defeitos.