Chapter 3 Ilustrando ideias

3.1 Exemplo - Distribuição Gaussiana

Suponha que \(Y_1, Y_2, \ldots, Y_n\) são variáveis aleatórias independentes e identicamente distribuídas com distribuição gaussiana de média \(\mu\) e variância \(\sigma^2\). Denote isto por \(Y_i \sim N(\mu, \sigma^2)\). Note que neste caso o vetor de parâmetros \(\underline{\theta} = (\mu, \sigma)^{\top}\). Onde \(\mu \in \Re\) e \(\sigma \in \Re^+\) são os respectivos espaços paramétricos. O objetivo é estimar \(\mu\) e \(\sigma\) além de encontrar intervalos ou regiões de confiança. Note que agora temos dois parâmetros e estamos trabalhando com uma superfície de log-verossimilhança. Os princípios vistos no caso uniparamétrico se mantém mas a construção de gráficos e a obtenção das estimativas são mais trabalhosas. Vejamos alguns fatos relevantes deste exemplo. Como sempre, começamos escrevendo a função de verossimilhança,

\[ L(\mu, \sigma) = (2\pi)^{-n/2} \sigma^{-n} \exp\{ - \frac{1}{2 \sigma^2} \sum_{i=1}^n (y_i - \mu)^2\}. \]

A log-verossimilhança é dada por,

\[ l(\mu,\sigma) = -\frac{n}{2} \log 2 \pi - n \log \sigma - \frac{1}{2 \sigma^2} \sum_{i=1}^n ( y_i - \mu)^2. \]

A função escore toma a forma de um sistema de equações,

\[\begin{align*} U(\mu) &= \frac{\partial l(\mu, \sigma)}{\partial \mu} = \frac{\sum_{i=1}^n y_i }{\sigma^2} - \frac{n \mu}{\sigma^2} \\ U(\sigma) &= -\frac{n}{\sigma} + \frac{1}{\sigma^3} \sum_{i=1}^n (y_i - \mu)^2 . \end{align*}\]

Neste caso podemos facilmente resolver este sistema chegando as estimativas de máxima verossimilhança,

\[ \hat{\mu} = \frac{\sum_{i=1}^n y_i}{n} \quad \text{e} \quad \hat{\sigma} = \frac{\sum_{i=1}^n (y_i - \mu)^2}{n}. \]

A matriz de informação observada fica da seguinte forma,

\[ I_O (\mu, \sigma) = \left[\begin{array}{cc} -\frac{\partial^2 l(\mu, \sigma)}{\partial \mu^2} & - \frac{\partial^2 l(\mu, \sigma)}{\partial \mu \partial \sigma} \\ - \frac{\partial^2 l(\mu, \sigma)}{\partial \mu \partial \sigma} & -\frac{\partial^2 l(\mu, \sigma)}{\partial \sigma^2} \end{array}\right] . \]

Temos então,

\[\begin{align*} \frac{\partial^2 l(\mu, \sigma)}{\partial \mu^2} &= \frac{\partial U(\mu)}{\partial \mu} = - \frac{n}{\sigma^2} \\ \frac{\partial^2 l(\mu, \sigma)}{\partial \sigma^2} &= \frac{\partial U(\sigma)}{\partial \sigma} = - \frac{2n}{\sigma^2} \\ \frac{\partial^2 l(\mu, \sigma)}{\partial \mu \partial \sigma} &= \frac{\partial U(\sigma)}{\partial \sigma} = -\frac{2}{\sigma^3} \sum_{i=1}^n (y_i - \overline{y}) = 0. \end{align*}\]

Logo,

\[ I_O(\hat{\mu}, \hat{\sigma}) = \left[\begin{array}{cc} \frac{n}{\hat{\sigma}^2} & 0 \\ 0 & \frac{2n}{ \hat{\sigma}^2} \end{array}\right] . \]

Neste caso a matriz de informação observada coincide com a matriz de informação esperada. Além disso, note a importante propriedade de ortogonalidade entre os parâmetros, indicada pelos termos fora da diagonal da matriz de informação serem zero. A derivada cruzada entre dois parâmetros ser zero, é condição suficiente para que estes parâmetros sejam ortogonais. A ortogonalidade é uma propriedade muito conveniente e simplifica as inferências, uma vez que podemos fazer inferência para um parâmetro sem nos preocupar com os valores do outro.

Para construção dos intervalos de confiança, a maneira mais direta é usar os resultados assintóticos dos estimadores de máxima verossimilhança, neste caso temos que a distribuição assintótica de \(\hat{\underline{\theta}} = (\hat{\mu}, \hat{\sigma})^\top\) é

\[ \begin{bmatrix} \hat{\mu} \\ \hat{\sigma} \end{bmatrix} \sim NM_2\left (\begin{bmatrix} \mu \\ \sigma \end{bmatrix} , \begin{bmatrix} \hat{\sigma}^2/n & 0 \\ 0 & \hat{\sigma}^2/2n \end{bmatrix} \right ) \]

Intervalos de confiança de Wald podem ser obtidos por:

\[ \hat{\mu} \pm z_{\alpha/2} \sqrt{\hat{\sigma}^2/n} \]

e para \(\sigma\) temos

\[ \hat{\sigma} \pm z_{\alpha/2} \sqrt{\hat{\sigma}^2/2n}. \]

A função de verossimilhança deste exemplo é simétrica e quadrática na direção de \(\mu\), e portanto a aproximação é exata. Porém a verossimilhança é assimétrica na direção de \(\sigma\). Destacamos ainda que a assimetria é maior \(\sigma^2\), um pouco menos acentuada em \(\sigma\) e ainda menos acentuada em \(\log(\sigma)\). Nos remetemos a discussão na Sessão 2.9 para mais detalhes e consequências. Na prática, se intervalos baseados na aproximação quadrática serão utilizados o mais recomendado então é parametrizar a função para uma forma mais próxima a simetria com \(\psi=\log(\sigma)\), obter intervalos para \(\psi\) e depois transformá-los para escala original do parâmetro, por transformação direta se verossimilhança em \(\psi\) for muito próxima à simetria ou caso contrário pelo método delta.

Outra opção é obter uma região de confiança baseada na deviance,

\[\begin{align*} D(\mu, \sigma) &= 2 [ l(\hat{\mu}, \hat{\sigma}) - l(\mu,\sigma)] \\ &= 2[ n \log \left( \frac{\sigma}{\hat{\sigma}} \right) + \frac{1}{2\sigma^2}\sum_{i=1}^n(y_i - \mu)^2 - \frac{1}{2\hat{\sigma}^2} \sum_{i=1}^n (y_i - \hat{\mu})]. \end{align*}\]

A deviance aproximada tem a seguinte forma

\[ D(\mu, \sigma) \approx ( \underline{\theta} - \underline{\hat{\theta}})^\top I_o(\underline{\hat{\theta}}) ( \underline{\theta} - \underline{\hat{\theta}}). \]

Note que neste caso a superfície de log-verossimilhança em duas dimensões esta sendo aproximada por uma elipse. É bastante intuitivo pensar que aproximar uma função em duas dimensões é mais difícil que em uma. Sabemos também que esta aproximação tenderá a ser melhor quanto maior for o tamanho da amostra. Para exemplificar esta ideia a Figura 3.1 apresenta o gráfico da função deviance bidimensional em \((\mu, \sigma)\) para o caso do modelo gaussiano para quatro tamanhos de amostra, n=10, 50, 100 e 1000.

Deviance exata (linha sólida) e aproximada (linha tracejada) para diferentes tamanhos de amostra - Distribuição Normal.

Figura 3.1: Deviance exata (linha sólida) e aproximada (linha tracejada) para diferentes tamanhos de amostra - Distribuição Normal.

Na Figura 3.1 vemos que com \(n=10\) a verossimilhança exibe forte assimetria na direção do parâmetro \(\sigma\) e a aproximação quadrática é claramente insatisfatória. Com o aumento do tamanho da amostra a aproximação quadrática vai ficando cada vez mais próxima da deviance exata, mais uma vez ilustrando o comportamento assintótico da verossimilhança. É importante notar também em modelos com dois ou mais parâmetros a aproximação pode melhorar mais rapidamente para um do que outro. No exemplo a aproximação é exata para \(\mu\) para qualquer tamanho de amostra. Já para \(\sigma\) é necessário um tamanho de amostra relativamente grande para que a deviance em sua direção tome um comportamento próximo do simétrico. A função se aproxima da simetria mais rapidamente se parametrizada com \(\log(\sigma)\).

Em outros modelos, como no caso dos modelos lineares generalizados (MLG) a intuição é a mesma ainda que a aproximação para parâmetros de média deixe de ser exata. De forma geral, para parâmetros de média a aproximação quadrática tende a apresentar bons resultados mesmo com amostras reduzidas. O mesmo não pode ser dito para parâmetros de dispersão ou mesmo de correlação. Em outras palavras, estimar a média é mais simples que estimar a variabilidade, que por sua vez é mais simples do que estimar correlações.

As regiões de confiança são as curvas de nível na superfície de deviance. Note que apenas com a deviance não temos intervalos marginais como os obtidos pela aproximação quadrática. Uma possível solução é projetar a superfície na direção do parâmetro de interesse na maior amplitude, que é obtida quando fixamos o outro parâmetro na sua estimativa de máxima verossimilhança. Porém esta prática só produz bons resultados quando os parâmetros são ao menos aproximadamente ortogonais. Uma solução mais genérica, ainda que computacionalmente mais trabalhosa é o obtenção das verossimilhanças perfilhadas.
No caso particular da distribuição gaussiana, que tem a propriedade de ortogonalidade entre \(\mu\) e \(\sigma\), a verossimilhança condicionada na estimativa de máxima verossimilhança coincide com a verossimilhança perfilhada. Para ilustrar este fato considere a obtenção da verossimilhança perfilhada para \(\mu\) e \(\sigma\) pelas funções a seguir:

Código 3.1 Função para log-verossimilhança perfilhada em relação aos parâmetros \(\mu\) e \(\sigma\) da distribuição gaussiana. 
## Perfil para mu
pl.mu <- function(sigma, mu, dados){
    pll <- sum(dnorm(dados, mean=mu, sd=sigma, log=TRUE))
    return(pll)}
## Perfil para sigma
pl.sigma <- function(mu, sigma, dados){
    pll <- sum(dnorm(dados, mean=mu, sd=sigma, log=TRUE))
    return(pll)}

Vamos criar uma malha de valores nos quais a função será avaliada para a construção dos gráficos. Também vamos obter a log-verossimilhança condicionada na estimativa de máxima verossimilhança, que consiste em avaliar apenas a função para um dos parâmetros com o outro fixado em sua estimativa.

set.seed(123)
y10 <- rnorm(10,10,1.5)
grid.mu <- seq(9, 11.3, length=200)
grid.sigma <- seq(0.65, 2.7, length=200)
## Condicional para mu:
mu.cond <- sapply(grid.mu, pl.sigma, sigma=sqrt(var(y10)*9/10), dados=y10)
## Condicional para sigma:
sigma.cond <- sapply(grid.sigma, pl.mu, mu=mean(y10), dados=y10)

Para obter o perfil de verossimilhança, por exemplo para \(\sigma\) precisamos de uma malha de valores de \(\sigma\) e para cada valor nesta malha encontrar o valor digamos \(\hat{\mu}_{\sigma}\) que maximiza a verossimilhança perfilhada. Para este exemplo existem formas fechadas para os estimadores, portanto basta aplicar a expressão do estimador de um parâmetro para cada valor na malha de valores do parâmetro sendo perfilhando. Entretanto para ilustração utilizamos uma forma mais geral, adequada para casos onde não há expressões fechadas, na qual maximizamos a função utilizando procedimentos numéricos, o que implica em uma otimização numérica de um parâmetro para cada valor na grade do parâmetro que está sendo perfilhado. Para a maximização usamos a função optimize() própria para maximização em apenas uma dimensão como é o caso neste exemplo. O código abaixo ilustra o procedimento para o conjunto de 10 dados. O gráfico da esquerda da Figura 3.2 mostra a superfície de deviance com as linhas tracejadas indicando os cortes para obtenção das deviances perfilhadas dos gráficos do centro e a direita. Nestes gráficos são também mostradas as funções deviance condicionadas no MLE (linha sólida).

mu.perf <- matrix(0, nrow=length(mu), ncol=2)
for(i in 1:length(mu)){
mu.perf[i,] <- unlist(optimize(pl.mu,c(0,200), 
                 mu=mu[i],dados=y10,maximum=TRUE))}

sigma.perf <- matrix(0, nrow=length(sigma), ncol=2)
for(i in 1:length(sigma)){
sigma.perf[i,] <- unlist(optimize(pl.sigma,c(0,1000), 
                sigma=sigma[i],dados=y10,maximum=TRUE))}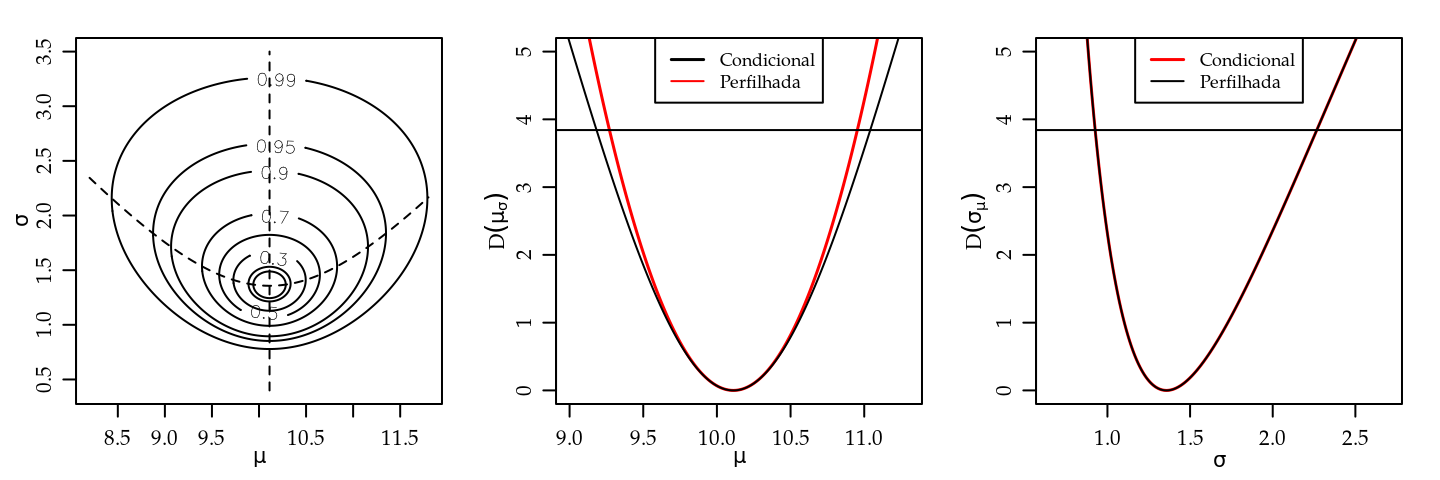
Deviance conjunta, perfilhada e condicional para $\mu$ e $\sigma$ - Distribuição Normal.

Figura 3.2: Deviance conjunta, perfilhada e condicional para \(\mu\) e \(\sigma\) - Distribuição Normal.

A Figura 3.2 ilustra que a deviance perfilhada e a deviance condicional coincidem para o parâmetro \(\sigma\) porém não para o parâmetro de média \(\mu\). Isto reflete o fato de que ao perfilhar \(\sigma\) o valor maximizado \(\hat{\mu}_{\sigma} = \hat{\mu}\) e não depende de \(\sigma\). Já no perfil de \(\mu\) cada um dos valores maximizados \(\hat{\sigma}_{\mu}\) dependem dos valores de \(\mu\). Para obter intervalos de confiança basta definir o corte nestas funções seja por valor relativo da verossimilhança ou usando o quantil da distribuição \(\chi^2\) para o nível de confiança desejado e encontrar as raízes da equação, assim como nos exemplos uniparamétricos. A verossimilhança perfilhada permite tratar um problema multiparamétrico como um problema uniparamétrico levando em consideração a forma da verossimilhança na direção de todos os parâmetros do modelo. Porém, esta abordagem pode ser extremamente cara computacionalmente, uma vez que para cada avaliação da verossimilhança perfilhada pode ser necessário uma maximização, que em geral vai requerer algum método numérico.

3.1.1 Dados intervalares

Quando definimos a função de verossimilhança no início deste capítulo, mencionamos que dados são medidos em algum intervalo definido pela precisão da medição. No exemplo anterior fizemos a suposição usual de que este intervalo é pequeno em relação a variação dos dados e portanto os valores dos dados são tratados como pontos na cálculo da função de verossimilhança e utilizamos (2.2)

Vamos considerar agora a situação na qual os dados são medidos em intervalos não desprezíveis. Desta forma voltamos a definição mais geral da verossimilhança em (2.1) para obter sua expressão.

Como exemplo vamos considerar a distribuição gaussiana \(Y_i \sim N(\mu, \sigma^2)\), \(\underline{\theta} = (\mu, \sigma)\). Suponha que temos um conjunto de dados que consiste de:

  • observações “pontuais”: \(\verb|72,6 81,3 72,4 86,4 79,2 76,7 81,3|\) ;

  • observações intervalares:

    • uma observação com valor acima de 85,
    • uma observação com valor acima de 80,
    • quatro observações com valores entre 75 e 80,
    • seis observações com valores abaixo de 75.

Supondo independência, a contribuição para verossimilhança das observações pontuais é o valor da densidade no ponto, enquanto que para as intervalares é a probabilidade da observação estar no intervalo. Para os tipos de dados neste exemplo temos: \[\begin{align*} L(\underline{\theta}) &= f(y_i) \mbox{ para } y_i \mbox{ pontual}, \\ L(\underline{\theta}) &= 1 - F(85) \mbox{ para } y_i > 85, \\ L(\underline{\theta}) &= 1 - F(80) \mbox{ para } y_i > 80, \\ L(\underline{\theta}) &= F(80) - F(75) \mbox{ para } 75 < y_i < 80,\\ L(\underline{\theta}) &= F(75) \mbox{ para } y_i < 85 . \end{align*}\]

A seguir escrevemos a função de (negativo da) verossimilhança que recebe como argumentos os parâmetros, os dados pontuais como um vetor e os intervalares como uma matriz de duas colunas na qual cada linha corresponde a um dado.

Código 3.2 Função para log-verossimilhança para dados pontuais e intervalares de distribuição gaussiana. 
nllnormI <- function(par, xp, XI){
    ## xp : vetor com observações "pontuais"
    ## XI: matrix (n x 2) com dados intervalares 
    ll1 <- sum(dnorm(xp, mean=par[1], sd=par[2], log=T))
    L2 <- pnorm(XI, mean=par[1], sd=par[2])
    ll2 <- sum(log(L2[,2] - L2[,1]))
    return(-(ll1 + ll2))
}

Nos comandos a seguir definimos os objetos que contém os dados. A matriz dos dados intervalares é transposta apenas para visualização Usamos estimativas baseadas nos dados completos como valores iniciais e encontramos as estimativas usando todos os dados maximizando e função de verossimilhança numericamente.

x <- c(72.6, 81.3, 72.4, 86.4, 79.2, 76.7, 81.3)        
t(xI <- cbind(c(85, 80, rep(75, 4), rep(-Inf, 6)),
              c(rep(Inf, 2), rep(80, 4), rep(75, 6))))
##      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12]
## [1,]   85   80   75   75   75   75 -Inf -Inf -Inf  -Inf  -Inf  -Inf
## [2,]  Inf  Inf   80   80   80   80   75   75   75    75    75    75
(ini <- c(mean(x), sd(x)))
## [1] 78.56  5.06
(ests <- optim(ini, nllnormI, xp=x, XI=xI)$par)
## [1] 76.67  5.72

Quando possível, é mais conveniente fazer o gráfico das superfícies de verossimilhança na escala da deviance que requer o valor da verossmimilhança avaliado nas estimativas dos parâmetros. Vamos utilizar a função deviance genérica definida em 3.3 que pode ser usada com outras densidades com dois parâmetros. Por conveniência definimos também a função em forma vetorizada que utilizaremos com o comando outer() na obtenção das superfícies.

Código 3.3 Função deviance genérica. 
devFun <- function(theta, est, llFUN, ...){
  return(2 * (llFUN(theta, ...) - llFUN(est, ...)))
}
devSurf <- Vectorize(function(x,y, ...) devFun(c(x,y), ...))

O gráfico à esquerda da Figura (fig:devNormalCens) mostra superfícies de verossimilhança na escala da deviance e é obtido com os comandos a seguir. As linhas tracejadas indicam o local do corte na superfície de deviance para obter a verossimilhança perfilhada. O gráfico da direita usa a parametrização \(\log(\sigma)\). O aspecto talvez mais importante é notar que, diferentemente dos gráficos 3.1, com dados intervalares a superfície não mais exibe ortogonalidade entre os parâmetros.

mu <- seq(70,82, l=100)
sigma <- seq(3, 14, l=100)
devMS <- outer(mu, sigma, FUN=devSurf, llFUN=nllnormI, 
               est=ests, yp=x, YI=xI)

LEVELS <- c(0.99,0.95,0.9,0.7,0.5,0.3,0.1,0.05)
contour(mu, sigma, devMS, levels=qchisq(LEVELS,df=2),
        labels=LEVELS, xlab=expression(mu),ylab=expression(sigma))
points(t(ests), pch=19, col=2, cex=0.7)

No código a seguir redefinimos a função de verossimilhança anterior acrescentando alguns elementos. Colocamos uma opção para parametrização usando \(\log(\sigma)\) através do argumento logsigma. Comandos para verificar se argumentos de dados foram informados permitem rodar a função mesmo sem dados pontuais ou intervalares. Finalmente verificamos internamente se a matriz de dados intervalares está especificada corretamente.

Código 3.4 Redefinição da função para log-verossimilhança para dados pontuais e intervalares de distribuição gaussiana. 
nllnormI <- function(par, xp, XI, logsigma=FALSE){
    if(logsigma) par[2] <- exp(par[2])
    ll1 <- ifelse(missing(xp), 0, 
             sum(dnorm(xp, mean=par[1], sd=par[2], log=T)))
    if(missing(XI)) ll2 <- 0
    else{ 
         if(ncol(XI) != 2 || any(XI[,2] <= XI[,1]))
           stop("XI deve ser matrix com 2 colunas com XI[,2] > XI[,2]")
         L2 <- pnorm(XI, mean=par[1], sd=par[2])
         ll2 <- sum(log(L2[,2] - L2[,1]))
    }
    return(-(ll1 + ll2))
}

Neste exemplo fizemos a suposição de distribuição gaussiana para os dados, mas os mesmos princípios e procedimentos são aplicáveis a outras distribuições. O procedimento pode ser usado com dados puramente intervalares como por exemplo dados agrupados. Suponha que os dados sejam provenientes de alguma fonte da qual
se tenha apenas a distribuição (tabela) de frequências. Podemos então definir a verossimilhança como no exemplo e obter as estimativas mesmo sem ter acesso aos dados originais, ainda que com menor precisão.

Dados intervalares são muitas vezes tratados pelo termo dados censurados, refletindo o fato de que o dado real não é observado devido a alguma restrição (censura). Tais dados podem ocorrer, por exemplo, devido a limites de detecção de aparelhos que podem ser incapazes de obter medidas acima (censura à direita) e/ou abaixo (censura à esquerda) de certos limites. Outra situação são medições que por alguma razão só podem ser feitas entre dois valores (censura intervalar). Dados censurados são discutidos em diversas áreas e entre elas são discutidos detalhadamente no escopo de análise de sobrevivência. Recomendamos os textos de Giolo and Colosimo (2006) e Carvalho et al. (2011) para leitores interessados no assunto.

3.1.2 Informação de cada dado

Na sessão anterior mostramos como dados pontuais e intervalares podem ser combinados na verossimilhança. Entretanto, a informação contida em cada um deles não é a mesma. É intuitivo que um dado pontual contém mais informação do que um intervalar, em especial em distribuições com um parâmetro de dispersão como a normal. Este fato pode ser visto e descrito na verossimilhança que pode ser feita para cada observação individualmente. A mais informativa vai ser mais “fechada,” ou seja exibir uma maior curvatura.

Para ilustrar vamos considerar o seguinte exemplo, adaptado de Pawitan (2001). Considere \(Y \sim N(\theta, 1)\) e as as seguintes observações:

  1. \(y=2.45\),
  2. \(0.9 < y < 4\),
  3. \(y_{(5)} = 3.5\) é o máximo de um grupo de cinco outras observações.

Sejam \(\phi(\cdot)\) e \(\Phi(\cdot)\) a densidade e densidade acumulada da normal padrão, respectivamente. A verossimilhança para cada uma das observações é calculada da seguinte forma:

\[\begin{align*} L(\theta; y) &= \phi(y-\theta) \equiv \frac{1}{\sqrt{2\pi}} \exp\{-\frac{1}{2} (y-\theta)^2\} ; \\ L_1 &= L(\theta; y=2.45) = \phi(y-\theta) = \frac{1}{\sqrt{2\pi}} \exp\{-\frac{1}{2} (2.45-\theta)^2\} ; \\ L_2 &= L(\theta; 0,9 < y < 4) = \Phi(4-\theta) - \Phi(0,9-\theta) ;\\ L_3 &= L(\theta; y_{(5)} = 3.5) = 5\{\Phi(y_{(n)} - \theta)\}^{5-1} \phi(y_{(5)} - \theta). \end{align*}\]

Note que a última verossimilhança decorre de um argumento multinomial e com \[F(y) = P(Y_{\{n\}} \leq y) = P[Y_{\{i\}} < y \;\forall i \neq n \mbox{ e } Y_{\{n\}} = y] \]

theta.vals <- seq(-0.5, 5.5, l=201)
L1 <- function(theta) dnorm(2.45, m=theta, sd=1)
L1.vals <- L1(theta.vals)
plot(theta.vals, L1.vals/max(L1.vals), ty="l", col=2, lty=2, 
     xlab=expression(theta), ylab=expression(LR(theta)))
##
L2 <- function(theta) 
        pnorm(4,mean=theta,sd=1)-pnorm(0.9,mean=theta,sd=1)
L2.vals <- L2(theta.vals)
lines(theta.vals, L2.vals/max(L2.vals), ty="l",  lty=5, 
      col="darkolivegreen")
##
L3 <- function(theta) 
        5*pnorm(3.5,m=theta,s=1)^4 * dnorm(3.5,m=theta,s=1)
L3.vals <- L3(theta.vals)
lines(theta.vals, L3.vals/max(L3.vals), ty="l", lty=4, col=4)

Pode-se ainda considerar a função de verossimilhança conjunta das três observações que, assumindo independência, é dada pelo produto da verossimilhanças individuais \(L(\theta) = L1 \cdot L2 \cdot L3\).

L4 <- function(theta)
  L1(theta) * L2(theta) * L3(theta)
L4.vals <- L4(theta.vals)
lines(theta.vals, L4.vals/max(L4.vals), ty="l")
legend("topright", c("y=2.45", "0,9<y<4", "y[5]=3.5", "conjunta"), 
       lty=c(2,3,4,1), col=c("red","darkolivegreen","blue","black"))

Curvas da função de log-verossimilhança \(l(\theta) = \log[L(\theta)]\) podem ser obtidas notando que, em geral, este é um cálculo computacionalmente mais adequado e estável. Outra alternativa é traçar curvas da função deviance \(D(\theta) = -2[l(\theta) - l(\hat{\theta})]\). Nos gráficos a seguir utilizamos um valor máximo computado para a sequência de valores para o parâmetro como uma aproximação de \(l(\hat{\theta})\). As funções de verossimilhança, log-verossimilhança e deviance (escalonadas) são mostradas na Figura 3.3. Notamos no gráfico as diferentes curvaturas para cada tipo de dado. O intervalar é o menos informativo, seguido pelo pontual. O máximo é mais informativo pois, além de ser pontual, temos também a informação de sua ordenação.

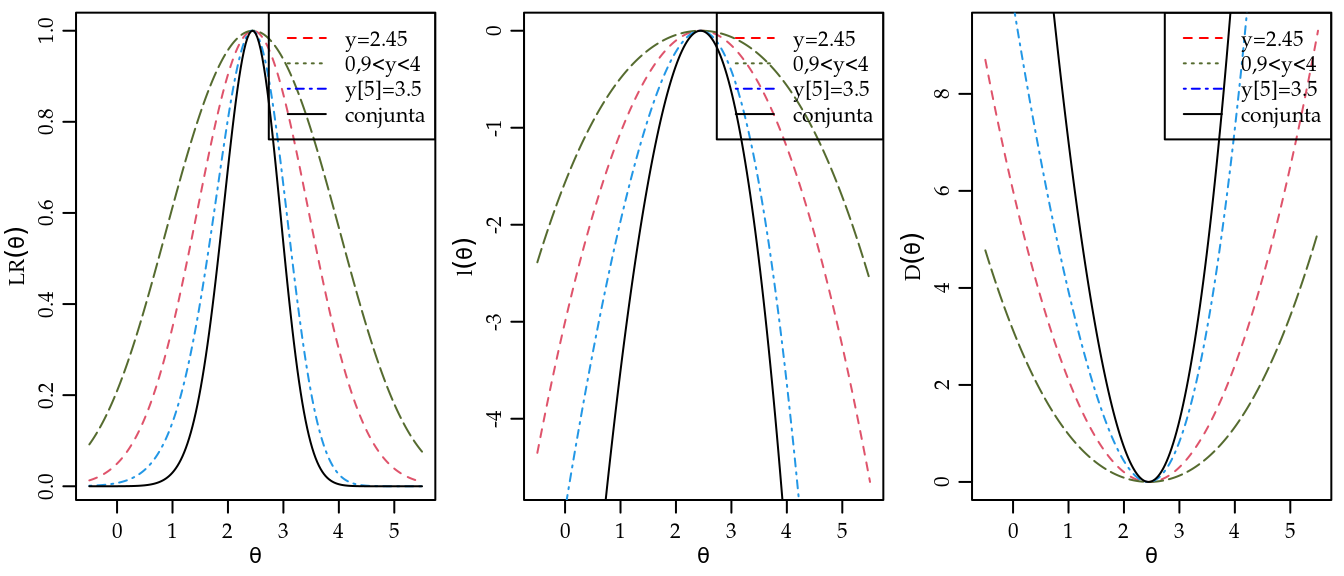
Verossimilhanças relativas, log-verossimilhanças e deviances para as observações individuais e a conjunta.

Figura 3.3: Verossimilhanças relativas, log-verossimilhanças e deviances para as observações individuais e a conjunta.

A estimativa do parâmetro pode ser obtida de forma usual maximizando a função de (log)verossimilhança conjunta das observações.

ll.ex3 <- function(theta){
  l1 <- -0.5 * (log(2*pi) + (2.45 - theta)^2)
  l2 <- log(pnorm(4, mean=theta, sd=1) - pnorm(0.9, mean=theta, sd=1))
  l3 <- log(5) + 4*pnorm(3.5, mean=theta, sd=1, log=T) + 
    dnorm(3.5, mean=theta, sd=1, log=T)
  return(l1+l2+l3)
}
optimize(ll.ex3, interval=c(0,5), maximum=TRUE)
## $maximum
## [1] 2.44
## 
## $objective
## [1] -1.54

3.2 Exemplo - Distribuição Gama

Sejam \(Y_1, Y_2, \ldots, Y_n\) variáveis aleatórias independentes com distribuição Gama de parâmetros \(a\) e \(s\). Nosso objetivo partindo de uma amostra aleatória \(y_1, y_2, \ldots y_n\) é fazer inferências sobre os seus dois parâmetros com seus respectivos intervalos de confiança baseados na aproximação quadrática e na função deviance. A função de densidade da distribuição Gama pode ser escrita na seguinte forma:

\[ f(y) = \frac{1}{s^a \Gamma(a)} y^{a-1} \exp\{-y/s\}, \quad \text{para} \quad y \ge 0 \quad \text{e} \quad a, s \ge 0. \]

Nesta parametrização \(E(Y) = a \cdot s\) e \(V(Y) = a \cdot s^2\). A função de verossimilhança é

\[\begin{align*} L(a,s) &= \prod_{i=1}^n (s^a \Gamma(a))^{-1} y_i^{a-1} \exp\{-y_i/s\} \\ &= s^{-na} \Gamma^{-n}(a) \exp\{-\sum_{i=1}^n y_i/s\} \prod_{i=1}^n y_i^{a-1}. \end{align*}\]

Esta parametrização da função gama é comumente encontrada, entretanto não é a mais conveniente para cálculos numéricos pois os parâmetros não são ortogonais. Vamos explorar estes fatos seguindo inicialmente com esta parametrização para ilustrar o comportamento da verossimilhança. Ao final passamos a uma forma reparametrizada mais conveniente para implementação de algoritmos.

A função de log-verossimilhança é dada por

\[ l(a,s) = -n a \log s - n \log \Gamma(a) - \frac{1}{s}\sum_{i=1}^n y_i + (a-1) \sum_{i=1}^n \log y_i. \]

As funções escore são obtidas derivando a log-verossimilhança em função de cada um dos respectivos parâmetros,

\[\begin{align*} U(a) &= -n \log (s) - n \frac{\Gamma'(a)}{\Gamma(a)} + \sum_{i=1}^n \log y_i \\ U(s) &= - \frac{na}{s} + \frac{1}{s^2} \sum_{i=1}^n y_i . \end{align*}\]

Para obter as estimativas de máxima verossimilhança igualamos essas expressões a zero e resolvemos em relação \(a\) e \(s\) o sistema de equações:

\[ \left\{\begin{align*} \log(s) + \Psi(a) &= \frac{1}{n} \sum_{i=1}^n \log y_i \\ a \cdot s &= \overline{y} \end{align*} \right. \]

em que \(\Psi(\cdot)\) é a função digama (digamma() no R) definida por \(\Psi(x) = \frac{d}{dx} \log \Gamma(x) = \Gamma'(x)/\Gamma(x)\). Este sistema claramente não tem solução analítica em \(a\), porém para \(s\) obtemos

\[\begin{equation} \hat{s} = \frac{\overline{y}}{a}. \tag{3.1} \end{equation}\]

Substituindo \(\hat{s}\) na função de log-verossimilhança, obtemos o que chamamos de log-verossimilhança concentrada em \(a\) com a expressão e escore dados por:

\[\begin{align} l_s(a) &= -n a \log \frac{\overline{y}}{a} - n \log \Gamma(a) - \frac{a}{\overline{y}} \sum_{i=1}^n y_i + (a-1) \sum_{i=1}^n \log y_i \\ \tag{3.2} U_s(a) &= -n \log(\overline{y}/a) - n \frac{\Gamma'(a)}{\Gamma(a)} + \sum_{i=1}^n \log y_i \tag{3.3} \end{align}\]

que são funções apenas do parâmetro \(a\). Com a verossimilhança concentrada reduzimos o problema original de maximização em duas dimensões, a uma maximação para apenas uma dimensão, o que é mais eficiente e estável computacionalmente. Para encontrar a estimativa de \(a\) ainda precisamos maximizar a log-verossimilhança concentrada numericamente. Para isto temos diferentes alternativas. Podemos usar um otimizador numérico como o implementado na função optimize() (para um parâmetro) ou alguns dos métodos da função optim() (para dois ou mais parâmetros) para maximizar (3.2). Alternativamente, podemos obter a estimativa igualando a equacão (3.3) a zero, e resolvendo numericamente, por exemplo com a função uniroot() do R. O pacote rootSolve implementa algoritmos adicionais incluindo a definição e solução de sistemas de equações.

Em geral, os métodos numéricos requerem valores iniciais para os parâmetros para inicializar o algoritmo. No caso da Gamma há uma escolha possível dos valores iniciais que seriam os estimadores pelo método dos momentos. Para a parametrização da Gama adotada aqui temos que as médias e variâncias populacionais e amostrais são:

\[\begin{align*} \mu &= E[Y] = a \cdot s \;\;\; &\sigma^2 &= Var[Y] = a \cdot s^2 \\ \hat{\mu} &= \frac{\sum_{i=1}^{n}Y_i}{n} = \bar{Y} \;\;\; &\hat{\sigma}^2 &= \frac{\sum_{i=1}^{n}(Y_i - \hat{Y})^2}{n} \end{align*}\]

Igualando os amostrais aos respectivos populacionais temos que estes estimadores são dados por:

\[ \hat{a}_M = \frac{\bar{Y}}{\hat{s}_M} \;\; \mbox{ e }\;\; \hat{s}_M = \frac{\hat{\sigma}^2}{\bar{Y}} . \]

Uma aproximação seria substituir \(\hat{sigma}^2\) pela variância amostral. O uso de bons valores iniciais garante um melhor comportamento dos algoritmos numéricos.

Mas antes disso, vamos investigar a ortogonalidade entre \(a\) e \(s\). Para isto, precisamos obter a matriz de segundas derivadas, neste caso de dimensão \(2 \times 2\), que fornece a matriz de informação observada e/ou esperada.

Derivando as funções escore temos,

\[\begin{align*} \frac{\partial^2 l(a,s)}{\partial a^2} &= -n \left [ \frac{\Gamma(a) \Gamma''(a) - \Gamma'(a)^2}{\Gamma(a)^2} \right ] \\ \frac{\partial^2 l(a,s)}{\partial s^2} &= \frac{na}{s^2} - \frac{2}{s^3} \sum_{i=1}^n y_i \\ \frac{\partial^2 l(a,s)}{\partial a \partial s} &= -\frac{n}{s}. \end{align*}\]

Logo, a matriz de informação observada é dada por,

\[ I_o(a,s) = \begin{bmatrix} n\left [ \frac{\Gamma''(a)}{\Gamma'(a)} - \left ( \frac{\Gamma'(a)}{\Gamma(a)} \right )^2 \right ] & \frac{n}{s} \\ \frac{n}{s} & - \frac{na}{s^2} + \frac{2}{s^3 \sum_{i=1}^n y_i} \end{bmatrix} . \]

A matriz esperada é obtida tomando a esperança da matriz observada, lembrando que \(E(Y) = a \cdot s\), temos

\[ I_E(a,s) = \begin{bmatrix} n\left [ \frac{\Gamma''(a)}{\Gamma(a)} - \left ( \frac{\Gamma'(a)}{\Gamma(a)} \right )^2 \right ] & \frac{n}{s} \\ \frac{n}{s} & \frac{na}{s^2}. \end{bmatrix} . \]

O termos fora da diagonal são não-nulos o que mostra que os parâmetros são não ortogonais. Para visualizarmos o formato da função de log-verossimilhança a Figura 3.4 apresenta a superfície de log-verossimilhança e sua aproximação quadrática em escala de deviance para facilitar a construção e visualização do gráfico. Os dados utilizados foram gerados da distribuiição Gama, com parâmetros \(a=10\) e \(s = 5\).

Deviance exata e aproximada por tamanho de amostra - Distribuição Gama.

Figura 3.4: Deviance exata e aproximada por tamanho de amostra - Distribuição Gama.

Pelos gráficos podemos ver claramente que quando o tamanho da amostra é pequeno \(n=10\) o formato da log-verossimilhança é extremamente assimétrico e consequentemente a aproximação quadrática é muito ruim. Com o aumento da amostra a aproximação quadrática vai melhorando, até que com \(n=2000\) a diferença é bastante pequena. Os gráficos também mostram a dependência entre os parâmetros \(a\) e \(s\), quando o \(a\) aumenta necessariamente o \(s\) diminui para manter a média que é \(a\cdot s\), além disso fica claro também que a incerteza associada a estimativa de \(a\) é muito maior quando comparada a estimativa de \(s\).

Agora retornamos à obtenção das estimativas de máxima verossimilhança. Lembrando que a log-verossimilhança concentrada (3.2) é uma função apenas do parâmetro \(a\), ama vez obtido a estimativa \(\hat{a}\) podemos substitui-la em \(\hat{s} = \frac{\overline{y}}{\hat{a}}\) e obter a estimativa de \(s\). Da mesma forma podemos substituir as estimativas nas matrizes de informação observada e esperada e encontrar intervalos de confiança assintóticos, sabendo que estes intervalos serão consistentes apenas com amostras grandes. Mas para todos estes procedimentos precisamos maximizar a log-verossimilhança concentrada em \(a\). A forma mais comum de fazer isso é usando o algoritmo de Newton-Raphson que utiliza a informação observada, ou uma variante deste chamada de algoritmo Escore de Fisher que substitui a informação observada pela esperada. Vamos abrir um parenteses e explicar rapidamente o algoritmo de Newton-Raphson.

O método de Newton-Raphson é usado para se obter a solução numérica de uma equação na forma \(f(x) = 0\), onde \(f(x)\) é contínua e diferenciável e sua equação possui uma solução próxima a um ponto dado. O processo de solução começa com a escolha do ponto \(x_1\) como a primeira tentativa de solução. A segunda tentativa, \(x_2\), é obtida a partir do cruzamento com o eixo \(x\) da reta tangente a \(f(x)\) no ponto \((x_1, f(x_1))\). A tentativa seguinte, \(x_3\) é a intersecção com o eixo \(x\) da reta tangente a \(f(x)\) no ponto \((x_2,f(x_2))\), e assim por diante. A equação de iteração é dada por:

\[\begin{equation} x_{i+1} = x_i - \frac{f(x_i)}{f'(x_i)} \end{equation}\]

ela é chamada de equação de iteração porque a solução é obtida com a aplicação repetida em cada valor sucessivo de \(i\) até que um critério de convergência seja atingido. Diversos critérios de convergência podem ser usados. Os mais comuns são:

  • Erro relativo \[ \left | \frac{x_{i+1} - x_i}{x_i} \right | \leq \epsilon \]
  • Tolerância em \(f(x)\) \[ | f(x_i)| \leq \delta \]

Uma função chamada NewtonRaphson() é definida em 3.5.

Código 3.5 Algoritmo genérico de Newton-Raphson. 
NewtonRaphson <- function(initial, escore, hessiano, tol=0.0001, 
                   max.iter, n.dim, print=FALSE, ...){
  solucao <- initial
  for(i in 2:max.iter){
    solucao <- initial - solve(hessiano(initial, ...), 
                escore(initial, ...))
    tolera <- abs(solucao - initial)
    if(all(tolera < tol) == TRUE)break
    initial <- solucao
    if(print) print(initial)
  }
  return(initial)
}

Note que para usar este algoritmo é necessário obter a primeira (escore) e a segunda (hessiano) derivada. Neste exemplo é possível obter expressões analíticas para ambas. Em modelos mais complexos expressões analíticas podem ser substituídas por gradientes e hessianos obtidos por algoritmos numéricos. Além disto, em certos casos o custo computacional em calcular o hessiano analítico pode ser muito maior que o numérico, o que acontece em alguns modelos multivariados que em geral envolvem muitas inversões de matrizes densas, fazendo com que este algoritmo se torne muito lento.

Cabe ressaltar que o método de Newton-Raphson é um algoritmo para encontrar raízes de uma equação que no caso da função escore leva as estimativas de máxima verossimilhança. Porém, existem diversos e poderosos algoritmos de maximização numérica que não exigem derivadas analíticas embora possam ser beneficiados com o uso de resultados destas principalmente a função escore. No R alguns destes maximizadores numéricos estão implementados na função optim().

Continuando com o exemplo da Gama, vamos obter a função escore e o hessiano da função de log-verossimilhança concentrada e usar o algoritmo de Newton-Raphson para obter a estimativa de \(a\).

A partir de (3.3) temos que:

\[\begin{align*} U_s(a) &= -n \log(\overline{y}/a) - n \Psi(a) + \sum_{i=1}^n \log y_i \\ U_s'(a) &= \frac{n}{a} - n \Psi'(a) \end{align*}\]

em que \(\Psi'(a)\) é a função trigama que é a derivada segunda do logaritmo da função gama.

Escrevendo estas funções em R temos o código 3.6.

Código 3.6 Função escore e hessiana ambas em relação ao parâmetro \(a\) da distribuição Gama. 
escore <- function(a,y){
  n <- length(y)
  u <- -n*log(mean(y)/a) - n*digamma(a) + sum(log(y))
  return(u)}

hessiano <- function(a,y){
  n <- length(y)
  u.l <- (n/a)-trigamma(a)*n
  return(u.l)}

Gerando 100 valores da distribuição Gama com parametros \(a = 10\) e \(s = 5\), obtemos os valores iniciais aproximados ou exatos correspondendo aos estimadores dos momentos:

set.seed(123)
y100 <- rgamma(100,shape=10,scale=5)
My <- mean(y100) ; Vy <- var(y100)
(initAprox <- c(My^2/Vy , Vy/My))
## [1] 13.30  3.68
n <- length(y100) ; Vy <- Vy * (n-1)/n
(init <- c(My^2/Vy , Vy/My))
## [1] 13.43  3.64

O passo final para obter a estimativa de máxima verossimilhança de \(a\) é usar o algoritmo de Newton-Raphson.

(a.hat <- NewtonRaphson(initial = init[1], escore = escore , 
       hessiano=hessiano, max.iter=100, n.dim=1, y=y100))
## [1] 13.5

Definindo o argumento print=TRUE é possível visualizar todas as tentativas do algoritmo até a convergência. Neste exemplo foi necessário seis iterações para atingir o critério de convergência. Uma limitação deste algoritmo é que o chute inicial não pode estar muito longe da solução, o que pode ser difícil de obter em modelos complexos, nestes casos estimativas grosseiras por mínimos quadrados podem ser de grande valia como valores iniciais.

Uma vez estimado o \(a\) podemos substituir na expressão de \(\hat{s}\) para obtê-lo,

(s.hat <- mean(y100)/a.hat)
## [1] 3.61

Para construção dos intervalos assintóticos basta substituir as estimativas nas matrizes de informação observada e/ou esperada. Note que, no caso da distribuição Gama a distribuição assintótica do vetor \((\hat{a},\hat{s})^\top\) é a seguinte,

\[ \begin{bmatrix} \hat{a} \\ \hat{s} \end{bmatrix} \sim NM_2 \left ( \begin{bmatrix} a \\ s \end{bmatrix}, \begin{bmatrix} n \Psi'(\hat{a}) & n /\hat{s} \\ n / \hat{s} & n\hat{a} / \hat{s}^2 \end{bmatrix}^{-1} \right ) \]

poderíamos usar também a matriz de informação observada que é assintoticamente equivalente. O código 3.7 implementa a matriz de informação esperada e observada e constrói os intervalos de confiança assintóticos para \(a\) e \(s\).

Código 3.7 Funções para a matriz de informação esperada e informação observada da distribuição Gama. 
Ie <- function(a,s,y){
  n <- length(y)
  saida <- matrix(c(n*trigamma(a),n/s,
          n/s, (n*a)/s^2),2,2)
  return(saida)}

Io <- function(a,s,y){
  n <- length(y)
  saida <- matrix(c(n*trigamma(a), n/s, n/s,
         -(n*a)/s^2 + (2/s^3)*sum(y)),2,2)
  return(saida)}

Avaliando as matrizes no ponto de máximo,

Ie(a = a.hat, s = s.hat, y=y100)
##       [,1]  [,2]
## [1,]  7.67  27.7
## [2,] 27.67 103.6
Io(a = a.hat, s = s.hat, y=y100)
##       [,1]  [,2]
## [1,]  7.67  27.7
## [2,] 27.67 103.6

Como é possível observar a matriz de informação esperada e observada apesar de apresentarem formas diferentes levam a resultados idênticos para o tamanho de amostra \(n=100\) considerado aqui. Sendo assim, vamos usar apenas a informação esperada que é mais simples de avaliar. Para obter os intervalos assintóticos basta inverter a matriz de informação e pegar os termos em sua diagonal que corresponde a variância de \(\hat{a}\) e \(\hat{s}\).

erro.padrao <- sqrt(diag(solve(Ie(a = a.hat, s= s.hat, y=y100))))
(ic.a <- a.hat + c(-1,1)*qnorm(0.975)*erro.padrao[1])
## [1]  9.83 17.24
(ic.s <- s.hat + c(-1,1)*qnorm(0.975)*erro.padrao[2])
## [1] 2.61 4.62

Outra forma é a construção de intervalos baseados no perfil de verossimilhança. As funções em 3.8 implementam o perfil de verossimilhança para os parâmetros \(a\) e \(s\), respectivamente.

Código 3.8 Funções para a log-verossimilhança perfilhada em relação aos parâmetros \(a\) e \(s\) da distribuição Gama. 
perf.a <- function(s, a, dados){
   ll <- sum(dgamma(dados, shape=a, scale=s, log=TRUE))
   return(ll)}
perf.s <- function(a, s, dados){
   ll <- sum(dgamma(dados, shape=a, scale=s, log=TRUE))
   return(ll)}

Para as maximizações necessárias vamos utilizar a função optimize() própria para maximização em uma dimensão como é o caso aqui. Precisamos também criar uma grade para a avaliação da função. Também será avaliada a verossimilhança condicional para comparação de forma similar ao mostrado no Exemplo 3.1. A Figura 3.5 apresenta os resultados.

grid.a <- seq(9,18,l=100)
grid.s <- seq(2,5,l=100)
## Perfil para a
vero.perf.a <- c()
for(i in 1:length(grid.a)){
vero.perf.a[i] <- optimize(perf.a,c(0,200), 
          a=grid.a[i],dados=y100,maximum=TRUE)$objective}

## Perfil para s
vero.perf.s <- c()
for(i in 1:length(grid.s)){
vero.perf.s[i] <- optimize(perf.s,c(0,1000), 
                  s=grid.s[i],dados=y100,maximum=TRUE)$objective}

## Condicional para a
vero.cond.a <- sapply(grid.a,perf.a,s=s.hat,dados=y100)

## Condicional para sigma
vero.cond.s <- sapply(grid.s, perf.s, a= a.hat , dados=y100)
Deviance perfilhada, condicional e limites do intervalo de confiança assintótico para $a$ e $s$ - Distribuição Gama.

Figura 3.5: Deviance perfilhada, condicional e limites do intervalo de confiança assintótico para \(a\) e \(s\) - Distribuição Gama.

Como mostra a Figura 3.5 os intervalos obtidos condicionando a log-verossimilhança na estimativa de máxima verossimilhança são claramente mais curtos que o intervalo baseado em perfil de verossimilhança e o intervalo assintótico. Comparando o perfil com o assintótico verificamos que a perfilhada traz intervalos ligeiramente assimétricos e mais largos que a aproximação quadrática, a aproximação é ligeiramente deslocada para esquerda e para direita para os parâmetros \(a\) e \(s\) respectivamente.

3.2.1 Parametrizações para Gama

Vamos explorar este exemplo para ilustrar o efeito de diferentes parametrizações no formato da verossimilhança da densidade Gama. Aproveitamos ainda esta sessão para ilustrar o uso de algumas sintaxes e formas de programação em R.

Parametrização 1: Esta é a parametrização utilizada anteriormente e também a usada nas funções *gamma do R. O parâmetro de forma (shape) é \(\alpha=a\) e o de escala (scale) \(\beta=s\). Lembrando as expressões obtidas anteriormente temos:

\[\begin{align*} Y &\sim {\rm G}(\alpha, \beta) \\ f(y|\alpha, \beta) &= \frac{1}{\Gamma(\alpha)\,\beta^\alpha}\;y^{\alpha-1}\;\exp\{-y/\beta\}\;\;\;; y \geq 0 \;,\; \alpha \geq 0 \;,\; \beta > 0 \\ E[Y] &= \alpha \beta \;\;\; Var[Y] = \alpha \beta^2 \\ L((\alpha,\beta)|y) &= \left(\frac{1}{\Gamma(\alpha) \, \beta^\alpha}\right)^n\; \prod_{i=1}^{n} y_i^{\alpha-1}\;\exp\{- \sum_{i=1}^{n} y_i/\beta\}\\ l((\alpha,\beta)|y) &= n\left(-\log(\Gamma(\alpha)) - \alpha \log(\beta) + (\alpha-1) \overline{\log(y)} - \bar{y}/\beta\right) \end{align*}\]

A função escore é escrita como:

\[\begin{align*} \left\{ \begin{array}{ll} \frac{d l}{d\beta} &= n\left(-\frac{\alpha}{\beta} + \frac{\bar{y}}{\beta^2}\right) \\ \frac{d l}{d\alpha} &= n \left(-\frac{\Gamma'(\alpha)}{\Gamma(\alpha)} -\log(\beta) + \overline{\log y}\right) \end{array} \right. \end{align*}\]

Igualando as funções a zero, da primeira equação temos \(\hat{\alpha} \hat{\beta} = \bar{y}\). Substituindo \(\beta\) por \(\hat{\beta}\) a segunda expressão é escrita como:

\[ n \left(-\frac{\Gamma'(\alpha)}{\Gamma(\alpha)} -\log\left(\frac{\bar{y}}{\hat{\alpha}}\right) + \overline{\log y}\right) = 0 \]

O EMV é portanto solução conjunta de

\[\begin{align*} \left\{\begin{array}{ll} \overline{\log y} - \log \beta &= \psi(\bar{y}/\beta)\\ \hat{\alpha} \hat{\beta} &= \bar{y} \end{array} \right. \end{align*}\]

em que

\(\psi(t) = \frac{d}{dt} \log(\Gamma(t)) = \frac{\Gamma'(t)}{\Gamma(t)}\) (função digamma() no R) e \(\overline{\log y} = \sum_{i=1}^n \log(y_i)/n\).

Parametrização 2: Esta parametrização utilizada por Rizzo (2008), dentre outros autores, é a parametrização original usada na linguagem S e sua primeira implementação no programa Splus (Splus e R são duas implementações em software, não completamente distintas, da linguagem Slang). Neste caso o parâmetro de escala é trocado pela seu inverso, a taxa (rate) e denotamos \(\lambda=1/\beta\). No R pode-se definir a escala ou taxa.

args(rgamma)
## function (n, shape, rate = 1, scale = 1/rate) 
## NULL

As expressões ficam então:

\[\begin{align*} Y &\sim {\rm G}(\alpha, \lambda) \\ f(y|\alpha, \lambda) &= \frac{\lambda^\alpha}{\Gamma(\alpha)}\;y^{\alpha-1}\;\exp\{-\lambda y\}\;\;\;; y \geq 0 \;,\; \alpha \geq 0 \;,\; \lambda > 0 \\ E[Y] &= \alpha/\lambda \;\;\; Var[Y] = \alpha / \lambda^2 \\ L((\alpha,\lambda)|y) &= \left(\frac{\lambda^\alpha}{\Gamma(\alpha)}\right)^n\; \prod_{i=1}^{n} y_i^{\alpha-1}\;\exp\{- \lambda \sum_{i=1}^{n} y_i\}\\ l((\alpha,\lambda)|y) &= n\left(\alpha \log(\lambda)-\log(\Gamma(\alpha)) + (\alpha-1) \overline{\log(y)} - \lambda\bar{y}\right) \end{align*}\]

Função escore:

\[\begin{align*} \left\{ \begin{array}{ll} \frac{d l}{d\lambda} &= n\left(\frac{\alpha}{\lambda} - \bar{y}\right) \\ \frac{d l}{d\alpha} &= n \left(\log(\lambda) - \frac{\Gamma'(\alpha)}{\Gamma(\alpha)} + \overline{\log y}\right) \end{array} \right. \end{align*}\]

Igualando as funções a zero, da primeira equação temos \(\hat{\lambda} = \hat{\alpha}/\bar{y}\). Substituindo \(\lambda\) por \(\hat{\lambda}\) a segunda expressão é escrita como:

\[n \left(\log \left(\frac{\hat{\alpha}}{\bar{y}} \right)+ \overline{\log y} - \frac{\Gamma'(\alpha)}{\Gamma(\alpha)}\right) = 0 \]

O EMV é solução conjunta de

\[\begin{align*} \left\{\begin{array}{ll} \log \lambda + \overline{\log y} &= \psi(\lambda \bar{y})\\ \bar{y} &= \alpha/\lambda \end{array} \right. \end{align*}\]

Aitkin (2010) menciona ainda duas parametrizações sendo a primeira considerada a mais usual, e sendo a mesma que é implementada no . Uma segunda é parametrizada por \(\alpha\) e \(\mu = \alpha \beta\) com o segundo parâmetro correspondente à média da variável.

Esta segunda parametrização tem propriedades interessantes para inferência. A primeira é a ortogonalidade na matriz de informação entre \(\alpha\) e \(\mu\). Além disto em geral \(\mu\) é o usualmente o parâmetro de interesse para inferências e \(\alpha\) é um parâmetro nuisance. A parametrização é adequada para modelagem estatística na qual usualmente se propõe um modelo de regressão para média \(\mu\), como por exemplo em modelos lineares generalizados (MLG).

\[\begin{align*} Y &\sim {\rm G}(\alpha, \mu) \\ f(y|\alpha, \mu) &= \frac{\alpha^\alpha}{\Gamma(\alpha)\,\mu^\alpha}\;y^{\alpha-1}\;\exp\{- \alpha y/\mu\}\;\;\;; y \geq 0 \;,\; \alpha \geq 0 \;,\; \mu \geq 0 \\ E[Y] &= \mu \;\;\; Var[Y] = \mu^2/\alpha \\ L((\alpha,\mu)|y) &= \left(\frac{\alpha^\alpha}{\Gamma(\alpha) \mu^\alpha}\right)^n \prod_{i=1}^{n} y_i^{\alpha-1}\;\exp\{- \alpha \sum_{i=1}^{n} y_i/\mu\}\\ l((\alpha,\mu)|y) &= n\left(\alpha (\log(\alpha) - \log(\mu)) - \log(\Gamma(\alpha)) + (\alpha-1) \overline{\log(y)} - \alpha\bar{y}/\mu \right) \end{align*}\]

Função escore

\[\begin{align*} \left\{ \begin{array}{ll} \frac{d l}{d\mu} &= n\left(-\frac{\alpha}{\mu} + \frac{\alpha\bar{y}}{\mu^2}\right) \\ \frac{d l}{d\alpha} &= n \left(\log(\alpha) + 1 - \log(\mu) - \frac{\Gamma'(\alpha)}{\Gamma(\alpha)} + \overline{\log y} - \frac{\bar{y}}{\mu}\right) \end{array} \right. \end{align*}\]

Igualando as funções a zero, da primeira equação temos \(\hat{\mu} = \bar{y}\). Substituindo \(\mu\) por \(\hat{\mu}\) a segunda expressão é escrita como:

\[n \left(\log \hat{\alpha} - \log(\bar{y}) - \frac{\Gamma'(\hat{\alpha})}{\Gamma(\hat{\alpha})} + \overline{\log y}\right) = 0 \]

O EMV é solução conjunta de:

\[\begin{align*} \left\{\begin{array}{ll} \log \hat{\alpha} - \psi(\hat{\alpha}) &= \log \bar{y} - \overline{\log y} \\ \hat{\mu} &= \bar{y} \end{array} \right. \end{align*}\]

Nesta parametrização, a partir das expressões de \(\frac{d^2 l}{d\mu^2}\) e \(\frac{d^2 l}{d\alpha^2}\) obtemos que os parametros são ortogonais na informação já que \(I_E(\mu,\alpha)\) e \(I_E(\hat{\mu},\hat{\alpha})\) são matrizes diagonais.

Para obter os gráficos de verossimilhança vamos definir uma função em R que será escrita com opção para as três parametrizações mencionadas. Em todas estas parametrizações os parâmetros são não negativos e uma transformação logarítmica fornece parâmetros com suporte na reta real, mas note que isto exclui o valor nulo do espaço paramétrico. Desta forma nossa função permite ainda reparametrizações adicionais trocando os parâmetros por seus logaritmos.

Código 3.9 Funções de verossimilhança de distribuição Gama, para diferentes parametrizações. 
neglLik <- function(par, amostra, modelo=2, logpar=FALSE){
  if(logpar) par <- exp(par)
  ll <- switch(modelo, 
    "1" = {alpha <- par[1]; beta <- par[2];
           with(amostra, n*(-alpha*log(beta)-log(gamma(alpha)) +  
                (alpha-1) * media.logs - media/beta))},
    "2" = {alpha <- par[1]; lambda <- par[2] ;
           with(amostra, n*(alpha*log(lambda)-log(gamma(alpha)) +  
                (alpha-1) * media.logs - lambda * media))},
    "3" = {alpha <- par[1]; mu <- par[2] ;
           with(amostra, n*(alpha*(log(alpha) - log(mu)) - 
                log(gamma(alpha)) +  (alpha-1) * media.logs - 
                (alpha/mu) * media))})
  return(-ll)
}

A função em 3.9 é escrita em termos de estatísticas (suficientes) da amostra para evitar repetições de cálculos e exige que estas quantidades sejam passadas na forma de uma lista nomeada pelo argumento amostra. A função retorna o negativo da verossimilhança. No exemplo a seguir começamos então simulando um conjunto de dados com \(\alpha=4.5\) e \(\beta=2\), e criamos o objeto com as estatísticas suficientes.

set.seed(201107)
dadosG <- rgamma(20, shape = 4.5, rate=2)
am <- list(media=mean(dadosG), media.logs = mean(log(dadosG)), 
           n=length(dadosG))

Quando possível, é mais conveniente fazer o gráfico das superfícies de verossimilhança na escala da deviance o que requer o valor máximo da verossimilhança. Assim, obtemos as estimativas de máxima verossimilhança para as 3 parametrizações, usando os códigos abaixo:

mod1 <- optim(c(1,1), neglLik, amostra=am, modelo=1)$par
mod2 <- optim(c(1,1), neglLik, amostra=am, modelo=2)$par
mod3 <- optim(c(1,1), neglLik, amostra=am, modelo=3)$par
cbind(mod1, mod2, mod3)
##       mod1 mod2 mod3
## [1,] 4.693 4.69 4.69
## [2,] 0.415 2.41 1.95

Neste ponto vamos simplesmente usar os objetos mod1, mod2 e mod3 que contém as estimativas. Mais adiante vamos discutir em mais detalhes a obtenção das estimativas.

Os comandos a seguir mostram como obter o gráfico da superfície de verossimilhança (deviance) para a parametrização~1. Utilizamos a função deviance genérica definida em 3.3 para ser usada com densidades com dois parâmetros. Definimos uma sequencia de valores para cada parâmetro e o valor da deviance é calculado em cada ponto da malha que combina os valores usando a função outer(). A partir da malha os contornos parametrização 1 na escala original dos parâmetros são desenhados na forma de isolinhas. Comandos análogos são usados para as demais parametrizações nas escalas originais e logarítmicas.

Na Figura 3.6 mostramos as superfícies para cada parametrização nas escalas originais e logarítmicas dos parâmetros. Simetria e ortogonalidade da superfície facilitam e melhoram o desempenho de algoritmos numéricos, sejam de optimização ou de algorítmos de amostragem como por exemplo os de MCMC (cadeias de Markov por Monte Carlo). A superfície de verossimilhança para a parametrização~3 é a que apresenta melhores características. Isto sugere que algorítimos de cálculos de verossimilhança em procedimentos numéricos utilizando a Gama devem ser escritos nesta parametrização transformando ao final os resultados para outras parametrizações de interesse, se for o caso.

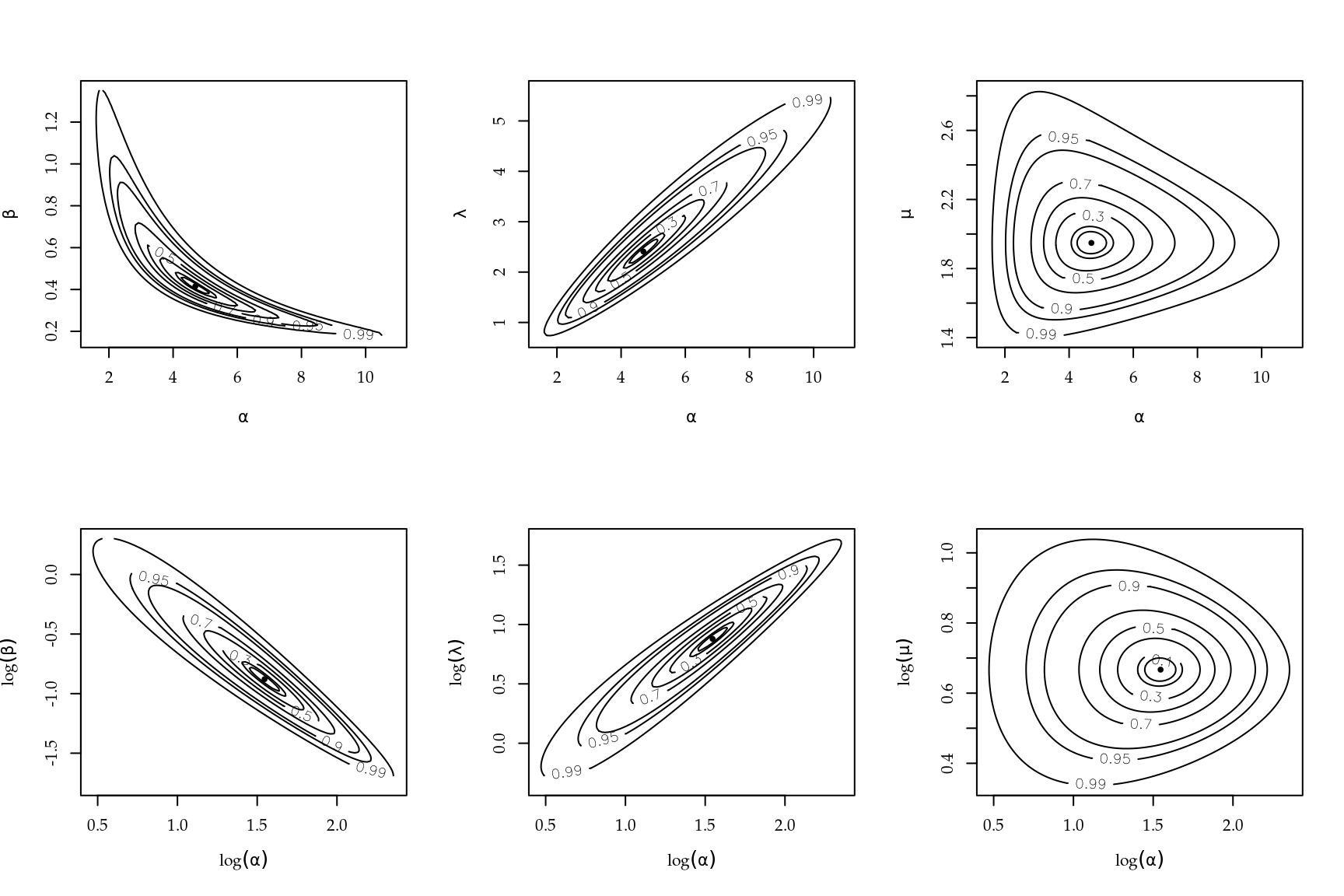
Superfícies de deviance sob diferentes parametrizações - Distribuição Gama.

Figura 3.6: Superfícies de deviance sob diferentes parametrizações - Distribuição Gama.

Neste exemplo passamos detalhadamente por cada passo do processo de inferência. Apresentamos o algoritmo de Newton-Raphson e comparamos três abordagens para a construção de intervalos de confiança. Há necessidade de uso intensivo de ferramentas do cálculo diferencial para obter a função escore e a matriz de informação. Destacou-se que nem sempre é fácil ou mesmo possível obter analiticamente as quantidades necessários para inferência.

3.3 Exemplo - Distribuição Binomial Negativa

Considere \(Y_1, Y_2, \ldots, Y_n\) variáveis aleatórias independentes provenientes de uma distribuição Binomial Negativa de parâmetros \(\phi \in \Re^+\) e \(0 < p \leq 1\) e \(y = 0,1, \ldots\). Usamos dados de uma amostra \(y_1, y_2, \ldots, y_n\) para estimar os parâmetros \(\phi\) e \(p\) e possivelmente construir intervalos de confiança e testes de hipóteses. Neste caso temos dois parâmetros, o que leva a uma superfície de verossimilhança. A função de distribuição da Binomial Negativa é dada por: \[ p(y) = \frac{\Gamma(y + \phi)}{\Gamma(\phi) y!} p^\phi (1 - p)^y, \quad \text{para} \quad 0 < p \leq 1 \quad \phi > 0 \quad \text{e} \quad y = 0, 1, 2 , \ldots . \]

Sendo \(n\) amostras independentes a função de verossimilhança tem a seguinte forma, \[\begin{align*} L(\phi,p) &= \prod_{i=1}^n \frac{\Gamma(y_i + \phi)}{\Gamma(\phi) y_i!} p^\phi (1 - p)^{y_{i}} \\ L(\phi,p) &= p^{n\phi} (1-p)^{\sum_{i=1}^n y_i} \prod_{i=1}^n \frac{\Gamma(y_i + \phi)}{\Gamma(\phi) y_i!}. \end{align*}\] Logo a função de log-verossimilhança pode ser escrita como, \[ l(\phi,p) = n \phi \log p + \sum_{i=1}^n y_i \log (1-p) + \sum_{i=1}^n \log \Gamma(y_i + \phi) - n \log \Gamma(\phi) - \sum_{i=1}^n \log y_i !. \] Derivando em relação aos parâmetros \(\phi\) e \(p\) obtém-se as equações escore: \[\begin{align*} U(\phi) &= n \log p + \sum_{i=1}^n \Psi(y_i + \phi) - n \Psi(\phi) \\ U(p) &= \frac{n \phi}{p} - \sum_{i=1}^n y_i / (1-p) \;. \end{align*}\] A matriz de informação é obtida calculando-se as derivadas: \[\begin{align*} \frac{\partial^2 l(\phi,p)}{\partial \phi^2} = \frac{\partial U(\phi)}{\partial \phi} & = \frac{\partial}{\partial \phi} \left[n \log p + \sum_{i=1}^n \Psi(y_i + \phi) - n \Psi(\phi)\right] \\ &= \sum_{i=1}^n \Psi'(y_i + \phi) - n \Psi'(\phi) \\ \frac{\partial^2 l(\phi, p)}{\partial p^2} = \frac{\partial U(p)}{\partial p} &= \frac{\partial}{\partial p} \left[\frac{n \phi}{p} - \sum_{i=1}^n y_i /(1-p) \right]\\ &= - \frac{n \phi}{p^2} - \sum_{i=1}^n y_i /(1-p)^2 \\ \frac{\partial l(\phi, p)}{\partial \phi \partial p} = \frac{\partial U(\phi)}{\partial p} &= \frac{\partial}{\partial p}\left[ n \log p + \sum_{i=1}^n \Psi(y_i + \phi) - n \Psi(\phi)\right] \\ &= \frac{n}{p}. \end{align*}\]

Com os resultados pode-se estimar \(\phi\) e \(p\) através do algoritmo de Newton-Raphson. Note que pela equação \(U(p)\) podemos obter a estimativa de \(p\) em função do parâmetro desconhecido \(\phi\) de forma análoga ao que acontece no modelo Gama. Entretanto, não vamos utiizar a verossimilhança concentrada para poder exemplificar o uso do algoritmo de Newton-Raphson em duas dimensões.

A implementação do modelo começa sempre com a construção da função de log-verossimilhança, o que fazemos em código que inicialmente reflete a forma que “escrevemos no papel.” Adiante veremos como usar as funções residentes do \(R\) para implementar um código mais eficiente. Uma amostra simulada de tamanho \(n=100\) e valores dos parâmetros \(\phi = 100\) e \(p = 0.8\) fornece os dados utilizados.

set.seed(123)
y <- rnbinom(100, size=100, p = 0.8)
Código 3.10 Função de log-verossimilhança para a distribuição binomial negativa. 
ll.neg.binomial <- function(par, y){
  phi <- par[1]
  p <- par[2]
  n <- length(y)
  ll <- n*phi*log(p) + sum(y)*log(1-p) + sum(log(gamma(y+phi))) - 
        n*log(gamma(phi)) - sum(log(factorial(y)))
  return(ll)}

Pensando em otimizar a função de log-verossimilhança através do algoritmo de Newton-Raphson, o próximo passo é implementar a função escore e, na sequência, a matriz de segundas derivadas ou Hessiana.

Código 3.11 Funções escore e hessiana para a distribuição binomial negativa. 
escore <- function(par, y){
  phi <- par[1]
  p <- par[2]
  n <- length(y)
  U.phi <- n*log(p) + sum(digamma(y+phi)) - n*digamma(phi)
  U.p <- (n*phi)/p - sum(y)/(1-p)
  return(c(U.phi,U.p))}
Hessiana <- function(par, y){
  phi = par[1]
  p = par[2]
  n <- length(y)
  II <- matrix(c(sum(trigamma(y+phi)) - n*trigamma(phi), 
               n/p,n/p, -(n*phi)/p^2 - sum(y)/(1-p)^2),2,2)
  return(II)}
NewtonRaphson(initial=c(50,0.5), escore=escore,hessiano=Hessiana,
              max.iter=100, tol = 1e-10, n.dim=2, y=y)
## [1] 114.198   0.821

Para construção do intervalo de confiança assintótico e/ou baseado em perfil de verossimilhança podemos proceder exatamente igual ao exemplo da distribuição Gama. Deixamos como exercício para o leitor obter estes intervalos e compará-los.