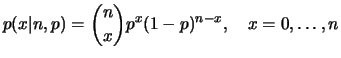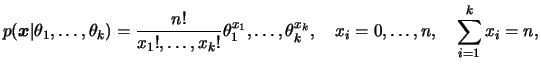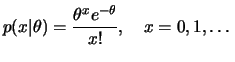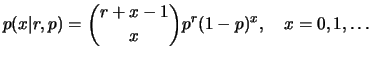


Next: Referências Bibliográficas
Up: Introdução a Inferência Bayesiana
Previous: 5. Exercícios
Sumário
Subsections
Neste apêndice são listadas as distribuições de probabilidade
utilizadas no texto para facilidade de referência. São apresentadas
suas funções de (densidade) de probabilidade além da média e
variância. Uma revisão exaustiva de distribuições de probabilidades
pode ser encontrada em Johnson et al. (1992, 1994, 1995).
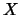 tem distribuição normal com parâmetros
tem distribuição normal com parâmetros 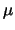 e
e 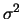 ,
denotando-se
,
denotando-se
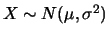 , se sua função de
densidade é dada por
para
, se sua função de
densidade é dada por
para
 e
e 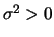 . Quando
. Quando 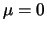 e
e 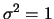 a
distribuição é chamada normal padrão. A distribuição log-normal é
definida como a distribuição de
a
distribuição é chamada normal padrão. A distribuição log-normal é
definida como a distribuição de 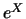 .
.
No caso vetorial,
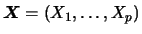 tem distribuição normal multivariada com vetor
de médias
tem distribuição normal multivariada com vetor
de médias 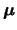 e matriz de variância-covariância
e matriz de variância-covariância 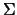 ,
denotando-se
,
denotando-se
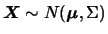 se sua função de
densidade é dada por
se sua função de
densidade é dada por
para
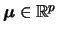 e
e 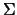 positiva-definida.
positiva-definida.
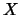 tem distribuição Gama com parâmetros
tem distribuição Gama com parâmetros 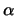 e
e 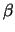 ,
denotando-se
,
denotando-se
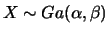 , se sua função de
densidade é dada por
para
, se sua função de
densidade é dada por
para
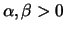 .
.
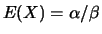
e
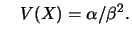
Casos particulares da distribuição Gama são a
distribuição de Erlang,
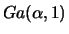 , a distribuição exponencial,
, a distribuição exponencial,
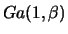 , e a distribuição qui-quadrado com
, e a distribuição qui-quadrado com 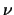 graus de
liberdade,
graus de
liberdade,
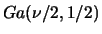 .
.
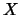 tem distribuição Gama Inversa com parâmetros
tem distribuição Gama Inversa com parâmetros 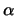 e
e 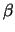 ,
denotando-se
,
denotando-se
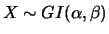 , se sua função de
densidade é dada por
para
, se sua função de
densidade é dada por
para
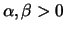 .
.
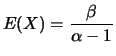
e
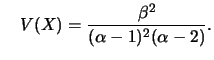
Não é difícil verificar que esta é a distribuição de 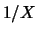 quando
quando
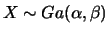 .
.
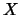 tem distribuição Beta com parâmetros
tem distribuição Beta com parâmetros 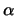 e
e 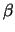 ,
denotando-se
,
denotando-se
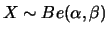 , se sua função de
densidade é dada por
para
, se sua função de
densidade é dada por
para
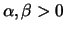 .
.
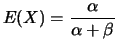
e
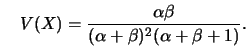
O vetor aleatório
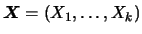 tem distribuição de
Dirichlet com parâmetros
tem distribuição de
Dirichlet com parâmetros
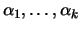 , denotada por
, denotada por
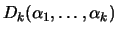 se sua função de
densidade conjunta é dada por
para
se sua função de
densidade conjunta é dada por
para
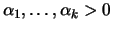 e
e
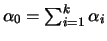 .
.
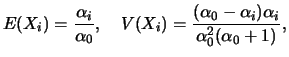
e
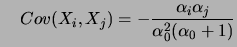
Note que a distribuição Beta é obtida como caso particular para 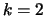 .
.
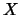 tem distribuição
tem distribuição 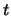 de Student (ou simplesmente
de Student (ou simplesmente 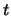 ) com média
) com média
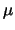 , parâmetro de escala
, parâmetro de escala 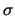 e
e 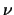 graus de liberdade,
denotando-se
graus de liberdade,
denotando-se
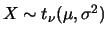 , se sua função de
densidade é dada por
para
, se sua função de
densidade é dada por
para 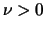 ,
,
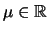 e
e 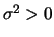 .
Um caso particular da distribuição
.
Um caso particular da distribuição 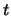 é a distribuição
de Cauchy, denotada por
é a distribuição
de Cauchy, denotada por 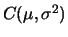 , que corresponde a
, que corresponde a 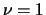 .
.
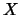 tem distribuição
tem distribuição 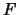 com
com 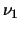 e
e 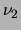 graus de liberdade,
denotando-se
graus de liberdade,
denotando-se
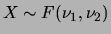 , se sua função de
densidade é dada por
, se sua função de
densidade é dada por
 , e para
, e para
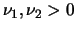 .
.
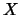 tem distribuição binomial com parâmetros
tem distribuição binomial com parâmetros 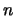 e
e 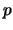 ,
denotando-se
,
denotando-se
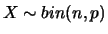 , se sua função de
probabilidade é dada por
para
, se sua função de
probabilidade é dada por
para 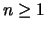 e
e 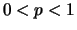 .
.
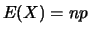
e
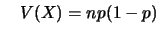
e um caso particular é a distribuição de Bernoulli com 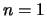 .
.
O vetor aleatório
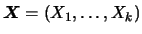 tem distribuição
multinomial com parâmetros
tem distribuição
multinomial com parâmetros 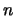 e probabilidades
e probabilidades
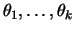 , denotada por
, denotada por
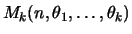 se sua função de
probabilidade conjunta é dada por
para
se sua função de
probabilidade conjunta é dada por
para
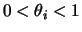 e
e
 . Note que a
distribuição binomial é um caso especial da multinomial quando
. Note que a
distribuição binomial é um caso especial da multinomial quando
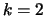 . Além disso, a distribuição marginal de cada
. Além disso, a distribuição marginal de cada 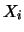 é binomial
com parâmetros
é binomial
com parâmetros 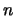 e
e 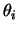 e
e
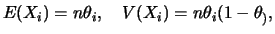
e
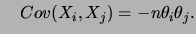
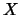 tem distribuição de Poisson com parâmetro
tem distribuição de Poisson com parâmetro  ,
denotando-se
,
denotando-se
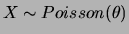 , se sua função de
probabilidade é dada por
para
, se sua função de
probabilidade é dada por
para 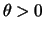 .
.
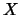 tem distribuição de binomial negativa com parâmetros
tem distribuição de binomial negativa com parâmetros 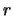 e
e 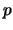 ,
denotando-se
,
denotando-se
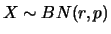 , se sua função de
probabilidade é dada por
para
, se sua função de
probabilidade é dada por
para 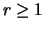 e
e 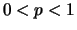 .
.
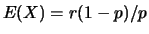
e
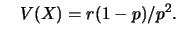



Next: Referências Bibliográficas
Up: Introdução a Inferência Bayesiana
Previous: 5. Exercícios
Sumário
Ricardo Ehlers & Paulo Justiniano
![]() tem distribuição normal multivariada com vetor
de médias
tem distribuição normal multivariada com vetor
de médias ![]() e matriz de variância-covariância
e matriz de variância-covariância ![]() ,
denotando-se
,
denotando-se
![]() se sua função de
densidade é dada por
se sua função de
densidade é dada por
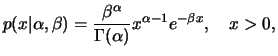
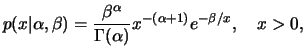
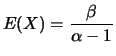 e
e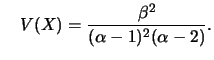
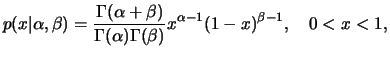
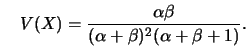
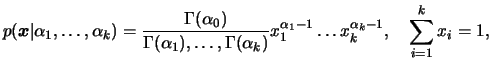
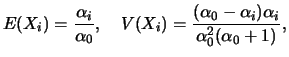 e
e![$\displaystyle p(x\vert\nu,\mu,\s)=
\frac{\Gamma((\nu+1)/2)\nu^{\nu/2}}{\Gamma(\...
...igma}
\left[\nu+\frac{(x-\mu)^2}{\s}\right]^{-(\nu+1)/2},\quad x\in\mathbb{R},
$](img739.png)
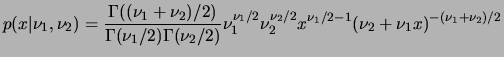
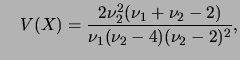 para
para