1. Introdução

A informação que se tem sobre uma quantidade de interesse $\theta$ é fundamental na Estatística. O verdadeiro valor de $\theta$ é desconhecido e a idéia é tentar reduzir este desconhecimento. Além disso, a intensidade da incerteza a respeito de $\theta$ pode assumir diferentes graus. Do ponto de vista Bayesiano, estes diferentes graus de incerteza são representados através de modelos probabilísticos para $\theta$. Neste contexto, é natural que diferentes pesquisadores possam ter diferentes graus de incerteza sobre $\theta$ (especificando modelos distintos). Sendo assim, não existe nenhuma distinção entre quantidades observáveis e os parâmetros de um modelo estatístico, todos são considerados quantidades aleatórias.

1.1 Teorema de Bayes

Considere uma quantidade de interesse desconhecida $\theta$ (tipicamente não observável). A informação de que dispomos sobre $\theta$, resumida probabilisticamente através de $p(\theta)$, pode ser aumentada observando-se uma quantidade aleatória $X$ relacionada com $\theta$. A distribuição amostral $p(x\vert\theta)$ define esta relação. A idéia de que após observar $X=x$ a quantidade de informação sobre $\theta$ aumenta é bastante intuitiva e o teorema de Bayes é a regra de atualização utilizada para quantificar este aumento de informação,

$$p(\theta\vert x)=\frac{p(\theta,x)}{p(x)}=\frac{p(x\vert\theta)p(... ...x2html_comment_mark>2 \frac{p(x\vert\theta)p(\theta)}{\int p(\theta,x)d\theta}.$$ (1.1)

Note que $1/p(x)$, que não depende de $\theta$, funciona como uma constante normalizadora de $p(\theta\vert x)$.

Para um valor fixo de $x$, a função $l(\theta;x)=p(x\vert\theta)$ fornece a plausibilidade ou verossimilhança de cada um dos possíveis valores de $\theta$ enquanto $p(\theta)$ é chamada distribuição a priori de $\theta$. Estas duas fontes de informação, priori e verossimilhança, são combinadas levando à distribuição a posteriori de $\theta$, $p(\theta\vert x)$. Assim, a forma usual do teorema de Bayes é

$$p(\theta\vert x) \propto l(\theta;x)p(\theta).$$ (1.2)

Em palavras temos que

   distribuição a posteriori$$\propto$$verossimilhança$$\times$$distribuição a priori$$.$$

Note que, ao omitir o termo $p(x)$, a igualdade em (1.1) foi substituída por uma proporcionalidade. Esta forma simplificada do teorema de Bayes será útil em problemas que envolvam estimação de parâmetros já que o denominador é apenas uma constante normalizadora. Em outras situações, como seleção de modelos, este termo tem um papel crucial.

É intuitivo também que a probabilidade a posteriori de um particular conjunto de valores de $\theta$ será pequena se $p(\theta)$ ou $l(\theta;x)$ for pequena para este conjunto. Em particular, se atribuirmos probabilidade a priori igual a zero para um conjunto de valores de $\theta$ então a probabilidade a posteriori será zero qualquer que seja a amostra observada.

A constante normalizadora da posteriori pode ser facilmente recuperada pois $p(\theta\vert x)=kp(x\vert\theta)p(\theta)$ onde

$$k^{-1}= \int p(x\vert\theta)p(\theta)d\theta=E_\theta[p(X\vert\theta)]= p(x)$$

chamada distribuição preditiva. Esta é a distribuição esperada para a observação $x$ dado $\theta$. Assim,

• Antes de observar $X$ podemos checar a adequação da priori fazendo predições via $p(x)$.

• Se $X$ observado recebia pouca probabilidade preditiva então o modelo deve ser questionado.

Se, após observar $X=x$, estamos interessados na previsão de uma quantidade $Y$, também relacionada com $\theta$, e descrita probabilisticamente por $p(y\vert\theta)$ então

$$p(y\vert x)=\int p(y,\theta\vert x)d\theta = \int p(y\vert\theta,x)p(\theta\vert x)d\theta$$

$$= \int p(y\vert\theta)p(\theta\vert x)d\theta$$

onde a última igualdade se deve a independência entre $X$ e $Y$ condicionado em $\theta$. Esta hipótese de independência condicional está presente em muitos problemas estatísticos. Note que as previsões são sempre verificáveis uma vez que $Y$ é uma quantidade observável. Finalmente, segue da última equação que

$$p(y\vert x) = E_{\theta\vert x}[p(Y\vert\theta)].$$

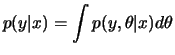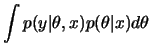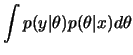Fica claro também que os conceitos de priori e posteriori são relativos àquela observação que está sendo considerada no momento. Assim, $p(\theta\vert x)$ é a posteriori de $\theta$ em relação a $X$ (que já foi observado) mas é a priori de $\theta$ em relação a $Y$ (que não foi observado ainda). Após observar $Y=y$ uma nova posteriori (relativa a $X=x$ e $Y=y$) é obtida aplicando-se novamente o teorema de Bayes. Mas será que esta posteriori final depende da ordem em que as observações $x$ e $y$ foram processadas? Observando-se as quantidades $x_1,x_2,\cdots,x_n$, independentes dado $\theta$ e relacionadas a $\theta$ através de $p_i(x_i\vert\theta)$ segue que

$$p(\theta\vert x_1) \propto l_1(\theta;x_1)p(\theta)$$

$$p(\theta\vert x_2,x_1) \propto l_2(\theta;x_2)p(\theta\vert x_1)$$

$$\propto l_2(\theta;x_2)l_1(\theta;x_1)p(\theta)$$

$$\vdots \vdots$$

$$p(\theta\vert x_n,x_{n-1},\cdots,x_1) \propto \left[\,\prod_{i=1}^n l_i(\theta;x_i)\right]p(\theta)$$

$$\propto l_n(\theta;x_n)\,p(\theta\vert x_{n-1},\cdots,x_1).$$

Ou seja, a ordem em que as observações são processadas pelo teorema de Bayes é irrelevante. Na verdade, elas podem até ser processadas em subgrupos.

(Gamerman e Migon, 1993) Um médico, ao examinar uma pessoa, `` desconfia'' que ela possa ter uma certa doença. Baseado na sua experiência, no seu conhecimento sobre esta doença e nas informações dadas pelo paciente ele assume que a probabilidade do paciente ter a doença é 0,7. Aqui a quantidade de interesse desconhecida é o indicador de doença

$$\theta = \left\{\begin{array}{l} 1,\quad \mbox{se o paciente tem ... ...a} \\ 0,\quad \mbox{se o paciente n\~ao tem a doen\c ca} \end{array}\right.$$

Para aumentar sua quantidade de informação sobre a doença o médico aplica um teste $X$ relacionado com $\theta$ através da distribuição

$$P(X=1~\vert~\theta=0)=0,40$$   e$$\qquad P(X=1~\vert~\theta=1)=0,95$$

e o resultado do teste foi positivo ($X=1$).

É bem intuitivo que a probabilidade de doença deve ter aumentado após este resultado e a questão aqui é quantificar este aumento. Usando o teorema de Bayes segue que

$$P(\theta=1~\vert~X=1)\propto l(\theta=1;X=1)p(\theta=1)=(0,95)(0,7)=0,665$$

$$P(\theta=0~\vert~X=1)\propto l(\theta=0;X=1)p(\theta=0)=(0,40)(0,3)=0,120.$$

A constante normalizadora é tal que $P(\theta=0~\vert~X=1)+P(\theta=1~\vert~X=1)=1$, i.e., $k(0,665)+k(0,120)=1$ e $k=1/0,785$. Portanto, a distribuição a posteriori de $\theta$ é

$$P(\theta=1~\vert~X=1)=0,665/0,785=0,847$$

$$P(\theta=0~\vert~X=1)=0,120/0,785=0,153.$$

O aumento na probabilidade de doença não foi muito grande porque a verossimilhança $l(\theta=0;X=1)$ também era grande (o modelo atribuia uma plausibilidade grande para $\theta=0$ mesmo quando $X=1$).

Agora o médico aplica outro teste $Y$ cujo resultado está relacionado a $\theta$ através da seguinte distribuição

$$P(Y=1~\vert~\theta=0)=0,04$$   e$$\qquad P(Y=1~\vert~\theta=1)=0,99.$$

Mas antes de observar o resultado deste teste é interessante obter sua distribuição preditiva. Como $\theta$ é uma quantidade discreta segue que

$$p(y\vert x)=\sum_\theta p(y\vert\theta)p(\theta\vert x)$$

e note que $p(\theta\vert x)$ é a priori em relação a $Y$. Assim,

$$P(Y=1~\vert~X=1) = P(Y=1~\vert~\theta=0)P(\theta=0~\vert~X=1)$$

$$+ P(Y=1~\vert~\theta=1)P(\theta=1~\vert~X=1)$$

$$= (0,04)(0,153) + (0,99)(0,847) = 0,845$$

$$P(Y=0~\vert~X=1) = 1-P(Y=1~\vert~X=1) = 0,155.$$

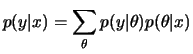
O resultado deste teste foi negativo ($Y=0$). Neste caso, é também intuitivo que a probabilidade de doença deve ter diminuido e esta redução será quantificada por uma nova aplicação do teorema de Bayes,

$$P(\theta=1~\vert~X=1,Y=0) \propto l(\theta=1;Y=0)P(\theta=1~\vert~X=1)$$

$$\propto (0,01)(0,847)=0,0085$$

$$P(\theta=0~\vert~X=1,Y=0) \propto l(\theta=0;Y=0)P(\theta=0~\vert~X=1)$$

$$\propto (0,96)(0,153)=0,1469.$$

A constante normalizadora é 1/(0,0085+0,1469)=1/0,1554 e assim a distribuição a posteriori de $\theta$ é

$$P(\theta=1~\vert~X=1,Y=0)=0,0085/0,1554=0,055$$

$$P(\theta=0~\vert~X=1,Y=0)=0,1469/0,1554=0,945.$$

Verifique como a probabilidade de doença se alterou ao longo do experimento

$$P(\theta=1)=\left\{\begin{array}{ll} 0,7, & \mbox{antes dos teste... ...{ap\'os o teste $X$} \\ 0,055, & \mbox{ap\'os $X$ e $Y$.} \end{array}\right.$$

Note também que o valor observado de $Y$ recebia pouca probabilidade preditiva. Isto pode levar o médico a repensar o modelo, i.e.,

(i) Será que $P(\theta =1)=0,7$ é uma priori adequada?

(ii) Será que as distribuições amostrais de $X$ e $Y$ estão corretas ? O teste $X$ é tão inexpressivo e $Y$ é realmente tão poderoso?

Um outro resultado importante ocorre quando se tem uma única observação da distribuição normal com média desconhecida. Se a média tiver priori normal então os parâmetros da posteriori são obtidos de uma forma bastante intuitiva.

Note que, definindo precisão como o inverso da variância, segue do teorema que a precisão a posteriori é a soma das precisões a priori e da verossimilhança e não depende de $x$. Interpretando precisão como uma medida de informação e definindo $w=\tau_0^{-2}/(\tau_0^{-2}+\sigma^{-2}) \in (0,1)$ então $w$ mede a informação relativa contida na priori com respeito à informação total. Podemos escrever então que

$$\mu_1=w\mu_0+(1-w)x$$

ou seja, $\mu_1$ é uma combinação linear convexa de $\mu_0$ e $x$ e portanto $\mu_0\le\mu_1\le x$.

(Box & Tiao, 1992) Os físicos $A$ e $B$ desejam determinar uma constante física $\theta$. O físico $A$ tem mais experiência nesta área e especifica sua priori como $\theta\sim N(900,20^2)$. O físico $B$ tem pouca experiência e especifica uma priori muito mais incerta em relação à posição de $\theta$, $%% \theta\sim N(800,80^2)$. Assim, não é difícil verificar que

para o físico $A$:$$\quad P(860<\theta<940)\approx 0,95$$

para o físico $B$:$$\quad P(640<\theta<960)\approx 0,95.$$

Faz-se então uma medição $X$ de $\theta$ em laboratório com um aparelho calibrado com distribuição amostral $X\vert\theta\sim N(\theta,40^2)$ e observou-se $X=850$. Aplicando o teorema 1.1 segue que

$$(\theta \vert X=850)\sim N(890,17,9^2)$$   para o físico $A$

$$(\theta \vert X=850)\sim N(840,35,7^2)$$   para o físico $B$$$.$$

Note também que os aumentos nas precisões a posteriori em relação às precisões a priori foram,

• para o físico $A$: precisão($\theta$) passou de $\tau_0^{-2}=0,0025$ para $\tau _1^{-2}=0,00312$ (aumento de 25%).

• para o físico $B$: precisão($\theta$) passou de $\tau_0^{-2}=0,000156$ para $\tau _1^{-2}=0,000781$ (aumento de 400%).

A situação está representada graficamente na Figura 1.1 a seguir. Note como a distribuição a posteriori representa um compromisso entre a distribuição a priori e a verossimilhança. Além disso, como as incertezas iniciais são bem diferentes o mesmo experimento fornece muito pouca informação adicional para o físico $A$ enquanto que a incerteza do físico $B$ foi bastante reduzida.

Figura: Densidades a priori e a posteriori e função de verossimilhança para o exemplo 1..2.

1.2 Princípio da Verossimilhança

O exemplo a seguir (DeGroot, 1970, páginas 165 e 166) ilustra esta propriedade. Imagine que cada item de uma população de itens manufaturados pode ser classificado como defeituoso ou não defeituoso. A proporção $\theta$ de itens defeituosos na população é desconhecida e uma amostra de itens será selecionada de acordo com um dos seguintes métodos:

(i) $n$ itens serão selecionados ao acaso.

(ii) Itens serão selecionados ao acaso até que $y$ defeituosos sejam obtidos.

(iii) Itens serão selecionados ao acaso até que o inspetor seja chamado para resolver um outro problema.

(iv) Itens serão selecionados ao acaso até que o inspetor decida que já acumulou informação suficiente sobre $\theta$.

Qualquer que tenha sido o esquema amostral, se foram inspecionados $n$ itens $x_1,\cdots,x_n$ dos quais $y$ eram defeituosos então

$$l(\theta;x)\propto \theta^y(1-\theta)^{n-y}.$$

O Princípio da Verossimilhança postula que para fazer inferência sobre uma quantidade de interesse $\theta$ só importa aquilo que foi realmente observado e não aquilo que `` poderia'' ter ocorrido mas efetivamente não ocorreu.

1.3 Exercícios

1. No exemplo 1..2, obtenha também a distribuição preditiva de $X$ e compare o valor observado com a média desta preditiva para os 2 físicos. Faça uma previsão para uma $2^{\underline{a}}$ medição $Y$ feita com o mesmo aparelho.

2. Uma máquina produz $5\%$ de itens defeituosos. Cada item produzido passa por um teste de qualidade que o classifica como `` bom '', `` defeituoso '' ou `` suspeito ''. Este teste classifica $20\%$ dos itens defeituosos como bons e $30\%$ como suspeitos. Ele também classifica $15\%$ dos itens bons como defeituosos e $25\%$ como suspeitos.

   (a) Que proporção dos itens serão classificados como suspeitos ? (b) Qual a probabilidade de um item classificado como suspeito ser defeituoso ? (c) Outro teste, que classifica $95\%$ dos itens defeituosos e $1\%$ dos itens bons como defeituosos, é aplicado somente aos itens suspeitos. (d) Que proporção de itens terão a suspeita de defeito confirmada ? (e) Qual a probabilidade de um item reprovado neste $2^{\underline{o}}$ teste ser defeituoso ?