- 2.6.1 Testes para Várias Médias
- 2.6.2 Variâncias Desconhecidas
- 2.6.3 Comparação de Variâncias
- Exercícios
Em geral, intervalos de confiança são a forma mais informativa de apresentar os achados principais de um estudo. Contudo, algumas vezes existe um particular interesse em verificar determinadas afirmações ou conjecturas. Por exemplo, podemos estar interessados em determinar se uma moeda é honesta, se certas quantidades são independentes, ou se populações distintas são similares do ponto de vista probabilístico. Cada uma destas afirmações constitui uma hipótese que pode ser associada a um modelo, i.e. pode ser parametrizada.
O material deste capítulo é fortemente baseado em deg89, Gamerman e Migon (1993) e Migon e Gamerman (1999). A teoria clássica de testes de hipóteses é apresentada a um nível mais formal em lehman86.
Chamamos de hipótese estatística qualquer afirmação que se faça
sobre um parâmetro populacional desconhecido. A idéia básica é que a
partir de uma amostra da população iremos estabelecer uma regra
de decisão segundo a qual rejeitaremos ou aceitaremos a hipótese
proposta. Esta regra de decisão é chamada de teste. Normalmente
existe uma hipótese que é mais importante para o pesquisador que será
denotada por ![]() e chamada hipótese nula. Qualquer outra
hipótese diferente de
e chamada hipótese nula. Qualquer outra
hipótese diferente de ![]() será chamada de hipótese alternativa
e denotada por
será chamada de hipótese alternativa
e denotada por ![]() . Veremos mais adiante que intervalos de confiança
e testes de hipóteses estão intimamente relacionados.
. Veremos mais adiante que intervalos de confiança
e testes de hipóteses estão intimamente relacionados.
Um professor aplica um teste do tipo certo-errado com 10 questões. Queremos testar a hipótese de que o aluno está advinhando.
Denotando por ![]() a probabilidade do aluno acertar cada questão a
hipótese estatística de interesse pode ser formulada como
a probabilidade do aluno acertar cada questão a
hipótese estatística de interesse pode ser formulada como
![]() Neste caso, a hipótese alternativa mais adequada é
Neste caso, a hipótese alternativa mais adequada é
![]() indicando que o aluno tem algum conhecimento sobre o assunto. Temos
então 10 repetições do experimento com
indicando que o aluno tem algum conhecimento sobre o assunto. Temos
então 10 repetições do experimento com ![]() constante, portanto
constante, portanto
![]() =''número de acertos'' tem distribuição binomial com parâmetros
=''número de acertos'' tem distribuição binomial com parâmetros
![]() e
e ![]() desconhecido. Suponha que adotamos a seguinte regra de
decisão: o aluno não está advinhando se acertar 8 ou mais
questões. Isto equivale a rejeitar
desconhecido. Suponha que adotamos a seguinte regra de
decisão: o aluno não está advinhando se acertar 8 ou mais
questões. Isto equivale a rejeitar ![]() se
se ![]() (região de
rejeição ou região crítica) e aceitar
(região de
rejeição ou região crítica) e aceitar ![]() se
se ![]() ( região de aceitação).
( região de aceitação).
No entanto, é possível que um aluno acerte 8 ou mais questões e esteja
advinhando, isto é podemos rejeitar ![]() quando ela é
verdadeira. A probabilidade de que isto ocorra é
quando ela é
verdadeira. A probabilidade de que isto ocorra é
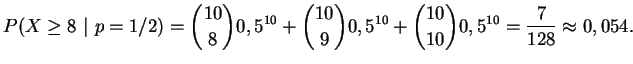
Um fornecedor garante que 90% de sua produção não apresenta defeito. Para testar esta afirmação selecionamos ao acaso 10 itens de um lote e contamos o número de defeituosos. Decidimos não comprar o lote se o número observado de não defeituosos for muito pequeno (mas quão pequeno?).
Definindo ![]() =''número de não defeituosos na amostra de 10 itens''
temos então uma distribuição binomial com parâmetros
=''número de não defeituosos na amostra de 10 itens''
temos então uma distribuição binomial com parâmetros ![]() e
e ![]() desconhecido, e queremos testar
desconhecido, e queremos testar
![]() . Aqui
. Aqui ![]() é a proporção
de itens não defeituosos no lote e portanto a hipótese alternativa
deve ser
é a proporção
de itens não defeituosos no lote e portanto a hipótese alternativa
deve ser
![]() . Suponha que decidimos manter
. Suponha que decidimos manter
![]() e a partir deste valor vamos estabelecer a nossa regra de
decisão. Para isto vamos calcular
e a partir deste valor vamos estabelecer a nossa regra de
decisão. Para isto vamos calcular ![]() para diferentes regiões
críticas, assim
para diferentes regiões
críticas, assim
Nestes dois exemplos os testes são chamados de unilaterais porque somente valores de um lado do espaço amostral foram utilizados para construir a região crítica. Podemos ter também testes bilaterais aonde os dois extremos do espaço amostral são usados como região crítica.
No caso geral então temos uma amostra aleatória
![]() tomada de uma distribuição que envolve um parâmetro
tomada de uma distribuição que envolve um parâmetro ![]() desconhecido, definido em um espaço paramétrico
desconhecido, definido em um espaço paramétrico ![]() . Assim, as
hipóteses podem ser definidas como
. Assim, as
hipóteses podem ser definidas como
![]() e
e
![]() onde
onde ![]() e
e ![]() são subconjuntos
disjuntos de
são subconjuntos
disjuntos de ![]() .
Um teste é
especificado particiondo-se o espaço amostral
em dois subconjuntos. Um sobconjunto contem os valores de
.
Um teste é
especificado particiondo-se o espaço amostral
em dois subconjuntos. Um sobconjunto contem os valores de ![]() para
os quais
para
os quais ![]() será rejeitada e é chamado região crítica do teste, e o
outro contem os valores de
será rejeitada e é chamado região crítica do teste, e o
outro contem os valores de ![]() para os quais
para os quais ![]() será aceita e é
chamado região de aceitação do teste. Em resumo, um teste fica
determinado quando especificamos sua região crítica.
será aceita e é
chamado região de aceitação do teste. Em resumo, um teste fica
determinado quando especificamos sua região crítica.
Além disso, uma hipótese pode ser classificada da seguinte maneira. Se
o subconjunto ![]() ,
, ![]() ou
ou ![]() contém um único valor então
contém um único valor então ![]() é
uma hipótese simples. Caso contrário, se
é
uma hipótese simples. Caso contrário, se ![]() contém mais de um
valor então
contém mais de um
valor então ![]() é uma hipótese composta. Nos exemplos 2..1 e
2..2
é uma hipótese composta. Nos exemplos 2..1 e
2..2 ![]() é uma hipótese simples enquanto
é uma hipótese simples enquanto ![]() é composta.
é composta.
Ao tomar uma decisão a favor ou contra uma hipótese existem dois tipos
de erros que podemos cometer. Podemos rejeitar a hipótese nula
quando de fato ela é verdadeira (erro tipo I) ou podemos falhar em
rejeitar ![]() quando de fato ela é falsa (erro tipo
II). Frequentemente denotamos as probabilidades
destes dois tipos de erro como
quando de fato ela é falsa (erro tipo
II). Frequentemente denotamos as probabilidades
destes dois tipos de erro como ![]() e
e ![]() respectivamente.
respectivamente.
Existe um
balanço entre esses dois tipos de erros, no sentido de que ao
tentar-se minimizar ![]() , aumenta-se
, aumenta-se ![]() . Isto é, não é
possível minimizar estas duas probabilidades simultaneamente e na
prática é costume fixar um valor (pequeno) para
. Isto é, não é
possível minimizar estas duas probabilidades simultaneamente e na
prática é costume fixar um valor (pequeno) para ![]() . Na Tabela
2.1 estão descritos as decisões que podemos tomar e os
tipos de erro associados.
. Na Tabela
2.1 estão descritos as decisões que podemos tomar e os
tipos de erro associados.
As características probabilísticas de um teste podem ser descritas
através de uma função que associa a cada valor de ![]() a
probabilidade
a
probabilidade
![]() de rejeitar
de rejeitar ![]() . A função
. A função
![]() é chamada função de poder (ou potência) do teste. Assim, denotando por
é chamada função de poder (ou potência) do teste. Assim, denotando por
![]() a região crítica a função de poder é definida como
a região crítica a função de poder é definida como
A função de poder é a ferramenta utilizada
para verificar a adequação de um teste ou para comparar dois ou mais
testes. É claro que uma função de poder ideal seria tal que
![]() para
para ![]() satisfazendo
satisfazendo ![]() e
e
![]() para
para ![]() satisfazendo
satisfazendo ![]() . Em um problema prático no entanto
raramente existirá um teste com estas características. Na Figura
2.1 abaixo está representada a função poder para o
exemplo 2..2, i.e.
. Em um problema prático no entanto
raramente existirá um teste com estas características. Na Figura
2.1 abaixo está representada a função poder para o
exemplo 2..2, i.e.
![]() , para
, para ![]() onde
onde
![]() . Note que neste exemplo se
. Note que neste exemplo se ![]() for
maior do que
digamos 0,8 então o teste quase certamente aceitará
for
maior do que
digamos 0,8 então o teste quase certamente aceitará ![]() , indicando
que o teste é adequado. Por outro lado, para valores de
, indicando
que o teste é adequado. Por outro lado, para valores de ![]() entre 0,7
e 0,8 o teste ainda rejeita
entre 0,7
e 0,8 o teste ainda rejeita ![]() com probabilidade baixa.
com probabilidade baixa.
O tamanho ou nível de significância ![]() de um teste é
definido como
de um teste é
definido como
Seja
![]() uma amostra aleatória
da distribuição
uma amostra aleatória
da distribuição
![]() com
com ![]() e suponha que queremos testar
e suponha que queremos testar
![]() . Suponha que a regra de decisão consiste em
rejeitar
. Suponha que a regra de decisão consiste em
rejeitar ![]() se somente se
se somente se
![]() . Neste
caso a função poder é dada por
. Neste
caso a função poder é dada por
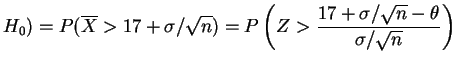
![$\displaystyle \sup_{\theta\le 17}
\left[P\left(Z>\frac{17+\sigma/\sqrt{n}-\theta}{\sigma/\sqrt{n}}\right)
\right]=P(Z>1)\approx 0,159
$](img218.png)
É mais útil começar o estuda da teoria de testes de hipóteses
considerando apenas hipóteses simples. Isto equivale a dizer que uma
amostra aleatória
![]() foi tomada de um dentre duas
possíveis distribuições e queremos decidir de qual delas vem a
amostra. Neste
caso o espaço paramétrico
foi tomada de um dentre duas
possíveis distribuições e queremos decidir de qual delas vem a
amostra. Neste
caso o espaço paramétrico ![]() contém apenas dois pontos, digamos
contém apenas dois pontos, digamos
![]() e
e ![]() e queremos testar
e queremos testar
As probabilidades dos dois tipo de erro são dadas por
[Teste Ótimo] Seja
![]() uma amostra aleatória de
uma distribuição com
função de (densidade) de probabilidade
uma amostra aleatória de
uma distribuição com
função de (densidade) de probabilidade
![]() e defina
e defina
![]() . Se um teste
. Se um teste ![]() rejeita
rejeita ![]() quando
quando
![]() , aceita
, aceita ![]() quando
quando
![]() e nada decide se
e nada decide se
![]() , então qualquer outro teste
, então qualquer outro teste ![]() é tal que
é tal que
A razão ![]() é chamada razão de verossimilhanças (RV). O
teorema estabelece então que um teste ótimo, no sentido de minimizar
é chamada razão de verossimilhanças (RV). O
teorema estabelece então que um teste ótimo, no sentido de minimizar
![]() , rejeita
, rejeita ![]() quando a razão de
verossimilhanças é pequena e aceita
quando a razão de
verossimilhanças é pequena e aceita ![]() quando esta razão é grande.
quando esta razão é grande.
Outro resultado vem do fato de que a hipótese ![]() e o erro tipo I são
em geral privilegiados em problemas práticos. Assim, é usual
considerar testes tais que
e o erro tipo I são
em geral privilegiados em problemas práticos. Assim, é usual
considerar testes tais que
![]() não seja maior do que um
nível especificado, digamos
não seja maior do que um
nível especificado, digamos ![]() , e tentar minimizar
, e tentar minimizar
![]() .
.
[Neyman-Pearson] Seja
![]() uma amostra aleatória de
uma distribuição com
função de (densidade) de probabilidade
uma amostra aleatória de
uma distribuição com
função de (densidade) de probabilidade
![]() e defina
e defina
![]() . Se um teste
. Se um teste ![]() rejeita
rejeita ![]() quando
quando
![]() , aceita
, aceita ![]() quando
quando
![]() e nada decide se
e nada decide se
![]() , então para qualquer outro teste
, então para qualquer outro teste ![]() tal que
tal que
![]() ,
,
![]() . E também,
. E também,
![]() implica em
implica em
![]() .
.
Seja
![]() uma amostra aleatória da distribuição
uma amostra aleatória da distribuição
![]() e queremos testar
e queremos testar
![]() . Neste caso a razão de
verossimilhanças é dada por
. Neste caso a razão de
verossimilhanças é dada por
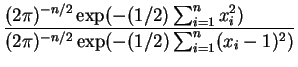 |
|||
![$\displaystyle \exp\left\{-\frac{1}{2}\left[\sum_{i=1}^n x_i^2 - \sum_{i=1}^n
(x_i-1)^2\right]\right\}$](img253.png) |
|||
![$\displaystyle \exp\left[-n\left(\overline{x}-\frac{1}{2}\right)\right].$](img254.png) |
Seja
![]() uma amostra aleatória da distribuição
exponencial com parâmetro
uma amostra aleatória da distribuição
exponencial com parâmetro ![]() e queremos testar
e queremos testar
![]() . A razão de
verossimilhanças é dada por
. A razão de
verossimilhanças é dada por
![$\displaystyle \frac{p_0}{p_1}=
\left(\frac{\theta_0}{\theta_1}\right)^n\exp\left[-(\theta_0-\theta_1)\sum_{i=1}^n
x_i\right]
$](img263.png)
![$\displaystyle \sum_{i=1}^n x_i >
\frac{1}{\theta_0-\theta_1}
\log\left[k\left(\frac{\theta_1}{\theta_0}\right)^n\right]=c
$](img264.png)
Vimos que a escolha do nível de significância do teste é completamente
arbitrária. Além disso, quando a distribuição da estatística
de teste é discreta, como no exemplo da binomial, o nível escolhido
pode nem mesmo ser atingido. Por outro lado, a decisão de aceitar ou
rejeitar ![]() claramente depende desta escolha. Na maioria das
aplicações práticas o valor escolhido é 0,05 ou 0,01 mas não há nada que
justifique formalmente o uso destes valores em particular.
claramente depende desta escolha. Na maioria das
aplicações práticas o valor escolhido é 0,05 ou 0,01 mas não há nada que
justifique formalmente o uso destes valores em particular.
Um enfoque alternativo consiste em calcular o menor nível de
significância para o qual ![]() é rejeitada, para o valor observado da
estatística de teste. Esta quantidade é chamada nível critico,
probabilidade de significância ou
p-valor. A idéia é que, após calcular o
é rejeitada, para o valor observado da
estatística de teste. Esta quantidade é chamada nível critico,
probabilidade de significância ou
p-valor. A idéia é que, após calcular o ![]() -valor o pesquisador
pode escolher o seu próprio nível de significância como sendo a
probabilidade máxima tolerável para um erro tipo I. Em geral, se
-valor o pesquisador
pode escolher o seu próprio nível de significância como sendo a
probabilidade máxima tolerável para um erro tipo I. Em geral, se ![]() é
uma estatística de teste e
é
uma estatística de teste e ![]() é rejeitada por exemplo para
é rejeitada por exemplo para ![]() então o
então o ![]() -valor é a probabilidade
-valor é a probabilidade
![]() onde
onde ![]() é o valor
observado de
é o valor
observado de ![]() .
.
No exemplo 2..1 suponha
que o número observado de questões certas foi ![]() . Então o
. Então o ![]() -valor será
-valor será
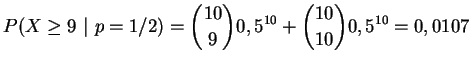
No exemplo 2..2 suponha que o número
observado de não defeituosos foi ![]() . Neste caso o
. Neste caso o ![]() -valor é dado por
-valor é dado por
Portanto, o ![]() -valor é a probabilidade de observar resultados
tão extremos quanto os obtidos se a hipótese nula for verdadeira. A
idéia é que se o
-valor é a probabilidade de observar resultados
tão extremos quanto os obtidos se a hipótese nula for verdadeira. A
idéia é que se o ![]() -valor for grande ele fornece evidência de que
-valor for grande ele fornece evidência de que ![]() é verdadeira, enquanto que um
é verdadeira, enquanto que um
![]() -valor pequeno indica que existe
evidência nos dados contra
-valor pequeno indica que existe
evidência nos dados contra ![]() . As seguintes interpretações de
. As seguintes interpretações de
![]() -valores (
-valores (![]() ) podem ser úteis,
) podem ser úteis,

Na Seção 2.2 foram definidos testes ótimos para testar
hipóteses simples. Nesta seção os resultados serão generalizados para
hipóteses compostas. Considere então um teste em que ![]() pode ser
uma hipótese simples ou composta e
pode ser
uma hipótese simples ou composta e ![]() é sempre uma hipótese composta.
é sempre uma hipótese composta.
Um teste ![]() de
de
![]() é dito ser uniformemente mais poderoso (UMP)
de tamanho
é dito ser uniformemente mais poderoso (UMP)
de tamanho ![]() se e somente se
se e somente se
A família exponencial inclui muitas das distribuições de probabilidade mais comumente utilizadas em Estatística, tanto contínuas quanto discretas. Uma característica essencial desta família é que existe uma estatística suficiente com dimensão fixa.
A família de distribuições com função de (densidade) de
probabilidade
![]() pertence à família exponencial a um
parâmetro se podemos escrever
pertence à família exponencial a um
parâmetro se podemos escrever
Se
![]() é uma amostra aleatória de um membro da
família exponencial e
é uma amostra aleatória de um membro da
família exponencial e ![]() for estritamente crescente em
for estritamente crescente em ![]() então o teste UMP de nível
então o teste UMP de nível ![]() para testar
para testar
![]() rejeita
rejeita ![]() se
se
![]() . Se as hipóteses forem invertidas ou
. Se as hipóteses forem invertidas ou ![]() for
estritamente decrescente em
for
estritamente decrescente em ![]() então o teste UMP rejeita
então o teste UMP rejeita ![]() se
se ![]() . Se ambas as condições ocorrerem o teste fica inalterado.
. Se ambas as condições ocorrerem o teste fica inalterado.
Um fato importante é que, em qualquer condição estes testes têm função
poder crescente em ![]() . Assim a constante
. Assim a constante ![]() acima é obtida de modo que
acima é obtida de modo que
![]() rejeitar
rejeitar ![]() , com igualdade no
caso contínuo.
, com igualdade no
caso contínuo.
Seja
![]() uma amostra aleatória da distribuição
de Bernoulli com parâmetro
uma amostra aleatória da distribuição
de Bernoulli com parâmetro ![]() e queremos testar
e queremos testar
![]() . Então, definindo
. Então, definindo
![]()
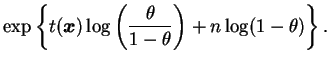 |
Seja
![]() uma amostra aleatória da distribuição
exponencial com parâmetro
uma amostra aleatória da distribuição
exponencial com parâmetro ![]() e queremos testar
e queremos testar
![]() . Definindo
. Definindo
![]() a densidade conjunta é
a densidade conjunta é
A propriedade que garante a existência de testes UMP na família exponencial pode ser extendida a famílias de distribuições com razão de verossimilhança monótona.
A família de distribuições com função de (densidade) de
probabilidade
![]() é dita ter razão de verossimilhança
monótona se existe uma estatística
é dita ter razão de verossimilhança
monótona se existe uma estatística ![]() tal que
tal que
![]() , com
, com
![]() , a
razão
, a
razão
![]() é uma função monótona em
é uma função monótona em
![]() .
.
Intuitivamente, quanto maior for a razão de verossimilhança mais
plausível é o valor ![]() em relação a
em relação a ![]() . Assim, se
queremos testar
. Assim, se
queremos testar
![]() e se
a RV for uma função crescente de
e se
a RV for uma função crescente de ![]() então é razoável rejeitar
então é razoável rejeitar
![]() para valores grandes de
para valores grandes de ![]() . Pode-se mostrar que neste
caso o teste UMP rejeita
. Pode-se mostrar que neste
caso o teste UMP rejeita ![]() se
se ![]() . Analogamente, se as
hipóteses forem invertidas ou se a RV for uma função decrescente de
. Analogamente, se as
hipóteses forem invertidas ou se a RV for uma função decrescente de
![]() então o teste UMP rejeita
então o teste UMP rejeita ![]() se
se ![]() . Se ambas as
condições ocorrerem o teste fica inalterado.
. Se ambas as
condições ocorrerem o teste fica inalterado.
Em qualquer destas condições o fato importante é que a função poder é
sempre crescente em ![]() . Portanto, a constante
. Portanto, a constante ![]() acima é obtida
de modo que
acima é obtida
de modo que
![]() rejeitar
rejeitar ![]() , com igualdade no
caso contínuo.
, com igualdade no
caso contínuo.
Seja
![]() uma amostra aleatória da distribuição
de Bernoulli com parâmetro
uma amostra aleatória da distribuição
de Bernoulli com parâmetro ![]() e queremos testar
e queremos testar
![]() . Então, definindo
. Então, definindo
![]() temos que
temos que
![$\displaystyle \frac{\theta_2^{t(\bfx)}(1-\theta_2)^{n-t(\bfx)}}
{\theta_1^{t(\b...
...a_2)}\right]^t
\left(\frac{1-\theta_2}{1-\theta_1}\right)^n = \alpha^t\beta^n.
$](img308.png)
Suponha agora que queremos testar hipóteses do tipo
Alternativamente poderiamos construir testes tais que as chances de rejeitar
![]() sejam maiores quando ela é falsa do que quando ela é
verdadeira. Isto nos leva à definição de testes não viesados a seguir.
sejam maiores quando ela é falsa do que quando ela é
verdadeira. Isto nos leva à definição de testes não viesados a seguir.
Um teste ![]() é dito ser não viesado para as
hipóteses
é dito ser não viesado para as
hipóteses
![]()
![]()
![]() se
se
![]()
![]() e
e
![]() então
então
![]() . Caso contrário o teste é dito viesado.
. Caso contrário o teste é dito viesado.
Ou seja, em testes não viesados a probabilidade de rejeitar ![]() quando ela é falsa é no mínimo tão grande quanto para
quando ela é falsa é no mínimo tão grande quanto para ![]() verdadeira.
verdadeira.
Podemos agora tentar construir testes para hipóteses bilaterais que
sejam UMP dentro da classe de testes não viesados. Se a distribuição
pertence à família exponencial, pode-se mostrar que se
![]() for uma função estritamente crescente em
for uma função estritamente crescente em ![]() então
o teste UMP não viesado de nível
então
o teste UMP não viesado de nível ![]() para
para
![]() aceita
aceita ![]() quando
quando
![]() . As constantes
. As constantes ![]() e
e ![]() são obtidas de modo que
são obtidas de modo que
![]() .
.
Note que existe uma infinidade de valores de ![]() e
e ![]() satisfazendo a esta condição. Em muitas situações é conveniente tomar
valores tais que
satisfazendo a esta condição. Em muitas situações é conveniente tomar
valores tais que
Outra característica dos testes bilaterias é que o ![]() -valor será a
soma de duas probabilidades. Assim, após observar a amostra temos um
valor
-valor será a
soma de duas probabilidades. Assim, após observar a amostra temos um
valor ![]() da estatística
da estatística ![]() e calculamos
e calculamos
Em muitas situações não é possível obter nem mesmo um teste não
viesado. Um procedimento geral para testar
![]()
![]()
![]() é baseado na estatística da razão de
máxima verossimilhança (RMV) dada por
é baseado na estatística da razão de
máxima verossimilhança (RMV) dada por
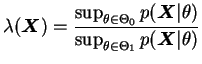
Além do cálculo de valores máximos da função de verossimilhança existe
outra dificuldade associada a estes testes que é a determinação da
distribuição amostral de
![]() . Este problema será discutido
quando falarmos de testes assintóticos na Seção 2.6.
. Este problema será discutido
quando falarmos de testes assintóticos na Seção 2.6.
Os resultados desenvolvidos nas seções anteriores serão
aplicados ao modelo normal para testes sobre média e variância em
problemas de uma ou mais amostras e em modelos de regressão
linear. Nesta seção considere uma amostra aleatória
![]() tomada da distribuição
tomada da distribuição
![]() .
.
Suponha que queremos testar
![]() e inicialmente vamos
assumir que
e inicialmente vamos
assumir que ![]() é conhecida. Neste caso,
é conhecida. Neste caso,
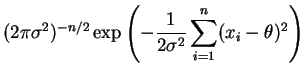 |
|||
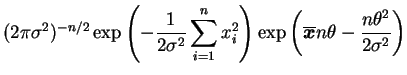 |
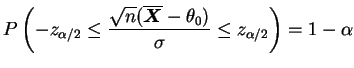
No caso em que a variância populacional é também desconhecida o espaço
dos parâmetro é
![]() e vamos
obter o teste da RMV. Note que, como
e vamos
obter o teste da RMV. Note que, como ![]() é uma hipótese simples
então
é uma hipótese simples
então
![]() e não é difícil verificar que
o valor de
e não é difícil verificar que
o valor de ![]() que maximiza a verossimilhança para
que maximiza a verossimilhança para ![]() fixo é
fixo é
![]() . Portanto,
. Portanto,
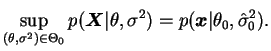
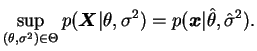
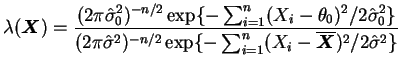
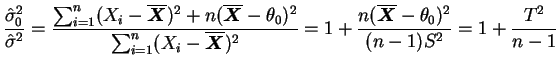
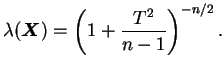
O teste desenvolvido acima é conhecido como teste ![]() e talvez um dos
mais utilizados em Estatística. Pode-se mostrar que o teste
e talvez um dos
mais utilizados em Estatística. Pode-se mostrar que o teste ![]() é não
viesado já que o valor mínimo da função poder ocorre em
é não
viesado já que o valor mínimo da função poder ocorre em
![]() . Além disso, as propriedades do teste não são
afetadas pelo valor de
. Além disso, as propriedades do teste não são
afetadas pelo valor de ![]() (parâmetro de distúrbio) já que
(parâmetro de distúrbio) já que ![]() foi
substituido pelo seu estimador
foi
substituido pelo seu estimador ![]() e
e ![]() é uma quantidade pivotal. O
teste também é invariante a transformações lineares das observações.
é uma quantidade pivotal. O
teste também é invariante a transformações lineares das observações.
Testes bilaterais do tipo
![]()
![]()
![]() para
a variância podem ser construídos fazendo-se
analogia com intervalos de confiança. Vimos na Seção 1.2.1 do
Capítulo 1 que o intervalo de confiança de
para
a variância podem ser construídos fazendo-se
analogia com intervalos de confiança. Vimos na Seção 1.2.1 do
Capítulo 1 que o intervalo de confiança de
![]() para
para ![]() é dado por
é dado por
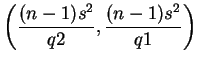
Para começar vamos assumir que temos duas amostras aleatórias
![]() e
e
![]() das distribuições
das distribuições
![]() e
e
![]() respectivamente e que as amostras são
independentes. Neste caso o vetor de parâmetros é
respectivamente e que as amostras são
independentes. Neste caso o vetor de parâmetros é
![]() e em geral estaremos interessados em
testar as hipóteses
e em geral estaremos interessados em
testar as hipóteses
Se pudermos assumir que as variâncias populacionais são
iguais, i.e.
![]() , o problema de construção do teste se torna
relativamente simples usando a estatística da razão de máxima
verossimilhança. Neste caso, como as amostras são
independentes, podemos escrever a função de verossimilhança como
, o problema de construção do teste se torna
relativamente simples usando a estatística da razão de máxima
verossimilhança. Neste caso, como as amostras são
independentes, podemos escrever a função de verossimilhança como
![$\displaystyle (2\pi\s)^{-(n_1+n_2)/2}
\exp\left\{
-\frac{1}{2\s}\left[
(n_1-1)S...
...overline{x}_1)^2+
(n_2-1)S_2^2+n_2(\theta_2-\overline{x}_2)^2
\right]\right\}.
$](img399.png)
Quando
![]() as estimativas de máxima verossimilhança de
as estimativas de máxima verossimilhança de
![]() ,
, ![]() e
e ![]() são respectivamente
são respectivamente
![]() ,
,
![]() e
e
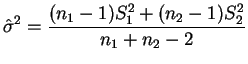
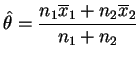 e
e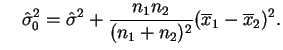
Substituindo estas expressões na razão de verossimilhanças pode-se
mostrar que o teste da RMV rejeita ![]() se
se
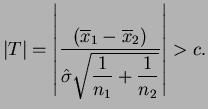
O procedimento visto na seção anterior para variâncias iguais pode ser
extendido facilmente para o caso de variâncias desconhecidas e
desiguais, desde que a razão de variâncias ![]() seja
conhecida. Suponha por exemplo que
seja
conhecida. Suponha por exemplo que
![]() onde
onde ![]() é uma
constante positiva conhecida. Definindo-se
é uma
constante positiva conhecida. Definindo-se
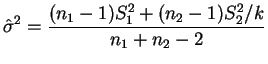
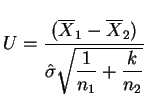
Finalmente, se mesmo a razão de variâncias for desconhecida então o problema de testar as hipóteses 2.1 torna-se bastante complexo. Este problema é conhecido na literatura como o problema de Behrens-Fisher. Vários procedimentos de teste já foram propostos e a maioria foi objeto de controvérsia em relação a sua utilidade e correção.
Em problemas com duas ou mais amostras de distribuições normais é
natural que se tenha
interesse em comparar as variâncias populacionais. Neste caso, a
distribuição ![]() é utilizada para testar as hipóteses associadas. No
caso de duas amostras suponha que queremos testar
é utilizada para testar as hipóteses associadas. No
caso de duas amostras suponha que queremos testar
Pode-se mostrar que não existe teste UMP para estas hipóteses e é
prática comum utilizar-se o chamado teste ![]() . Este teste é não
viesado e na verdade é UMP dentro da classe de testes não
viesados. Usando a estatística da razão de máxima verossimilhança
pode-se mostrar que o teste
. Este teste é não
viesado e na verdade é UMP dentro da classe de testes não
viesados. Usando a estatística da razão de máxima verossimilhança
pode-se mostrar que o teste ![]() rejeita
rejeita ![]() se
se
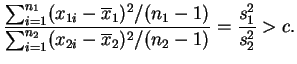
Vimos na Seção 1.2.4 que
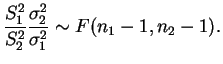
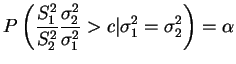
No caso de testes bilaterais, i.e.


Vimos que a construção de um teste envolve a obtenção de constantes através da distribuição de probabilidades de uma estatística. Em muitas situações, particularmente para a razão de máxima verossimilhança, estas distribuições não podem ser determinadas de forma exata e precisamos recorrer a resultados aproximados. Nesta seção serão desenvolvidos testes baseados em distribuições assintóticas das estatísticas de teste envolvidas. Iremos nos concentrar em testes baseados na distribuição assintótica da razão de máxima verossimilhança, do estimador de máxima verossimilhança e da função escore.
Suponha que uma amostra aleatória
![]() é tomada de uma
distribuição com parâmetro
é tomada de uma
distribuição com parâmetro
![]() desconhecido e queremos testar
desconhecido e queremos testar
![]() . Expandindo em
série de Taylor a função
. Expandindo em
série de Taylor a função
![]() em torno
do estimador de máxima verossimilhança
em torno
do estimador de máxima verossimilhança
![]() obtemos
obtemos
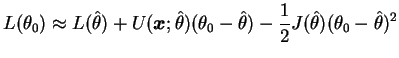
Mas função escore avaliada em
![]() é igual a zero por
definição. Além disso, a razão de máxima verossimilhança neste caso é
é igual a zero por
definição. Além disso, a razão de máxima verossimilhança neste caso é

![$\displaystyle -2\log\lambda(\bfX)=
-2\log\left(\frac{p(\bfX\vert\theta_0)}{p(\b...
...L(\theta_0)-L(\hat{\theta})]\approx
J(\hat{\theta})(\theta_0-\hat{\theta})^2.
$](img459.png)
Este resultado pode ser generalizado para o caso de um vetor de
parâmetros
![]() de dimensão
de dimensão ![]() . Neste
caso, a estatística
. Neste
caso, a estatística
![]() tem distribuição assintótica
tem distribuição assintótica
![]() .
.
Um caso de particular interesse em Estatística é quando os dados são tais que cada observação pode ser classificada de acordo com um número finito de possíveis categorias. Por isso, observações deste tipo são chamadas dados categóricos e estaremos interessados em fazer inferência sobre as probabilidades de cada categoria.
Suponha que uma população consiste de itens que podem ser
classificados em ![]() diferentes categorias. Seja
diferentes categorias. Seja ![]() a
probabilidade de que um item selecionado ao acaso pertença à categoria
a
probabilidade de que um item selecionado ao acaso pertença à categoria
![]() ,
,
![]() . Assumimos também que
. Assumimos também que
![]() ,
,
![]() e
e
![]() . Sejam agora os valores específicos
. Sejam agora os valores específicos
![]() tais que
tais que
![]() ,
,
![]() e
e
![]() e queremos testar as hipóteses
e queremos testar as hipóteses
Suponha agora que uma amostra aleatória de tamanho ![]() é tomada desta
população e as hipóteses (2.2) serão testadas com base nesta
amostra. Para isto vamos denotar
é tomada desta
população e as hipóteses (2.2) serão testadas com base nesta
amostra. Para isto vamos denotar ![]() o número amostral de
observações na categoria
o número amostral de
observações na categoria ![]() , i.e.
, i.e.
![]() são inteiros não
negativos tais que
são inteiros não
negativos tais que
![]() . Quando
. Quando ![]() é verdadeira, o
número esperado de observações do tipo
é verdadeira, o
número esperado de observações do tipo ![]() é
é ![]() e a diferença
entre o número observado e o número esperado tende a ser menor quando
e a diferença
entre o número observado e o número esperado tende a ser menor quando
![]() é verdadeira do que quando ela é falsa. Parece razoável então
basear o teste nas magnitudes relativas destas diferenças. Neste caso,
usando-se a função escore pode-se mostrar que o teste assintótico
rejeita
é verdadeira do que quando ela é falsa. Parece razoável então
basear o teste nas magnitudes relativas destas diferenças. Neste caso,
usando-se a função escore pode-se mostrar que o teste assintótico
rejeita ![]() se
se
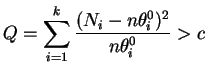
Uma observação de ordem prática é que as frequências esperadas
![]() não devem ser muito pequenas para que a distribuição
não devem ser muito pequenas para que a distribuição
![]() seja uma boa aproximação da distribuição de
seja uma boa aproximação da distribuição de
![]() . Especificamente, pode-se mostrar que a aproximação será muito boa
se
. Especificamente, pode-se mostrar que a aproximação será muito boa
se
![]() e apenas razoável
e apenas razoável
![]() .
.
Várias aplicações para dados categóricos e métodos não paramétricos que utilizam testes qui-quadrado podem ser vistas por exemplo em deg89.