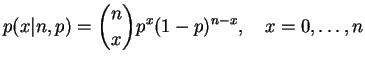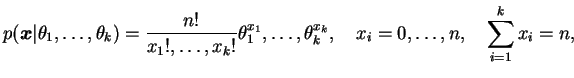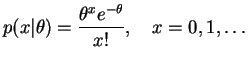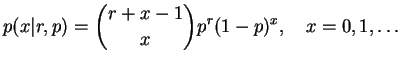


Next: Referências Bibliográficas
Up: CE-210 Inferência Estatística II
Previous: 2. Testes de Hipóteses
Sumário
Subsections
Neste apêndice são listadas as distribuições de probabilidade
utilizadas no texto para facilidade de referência. São apresentadas
suas funções de (densidade) de probabilidade além da média e
variância. Uma revisão exaustiva de distribuições de probabilidades
pode ser encontrada em Johnson et al. (1992, 1994, 1995).
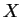 tem distribuição normal com parâmetros
tem distribuição normal com parâmetros 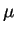 e
e 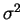 ,
denotando-se
,
denotando-se
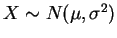 , se sua função de
densidade é dada por
para
, se sua função de
densidade é dada por
para
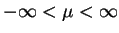 e
e 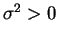 . Quando
. Quando 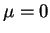 e
e 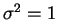 a
distribuição é chamada normal padrão. A distribuição log-normal é
definida como a distribuição de
a
distribuição é chamada normal padrão. A distribuição log-normal é
definida como a distribuição de 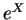 .
.
No caso vetorial,
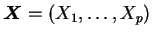 tem distribuição normal multivariada com vetor
de médias
tem distribuição normal multivariada com vetor
de médias 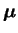 e matriz de variância-covariância
e matriz de variância-covariância 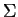 ,
denotando-se
,
denotando-se
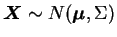 se sua função de
densidade é dada por
se sua função de
densidade é dada por
para
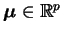 e
e 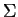 positiva-definida.
positiva-definida.
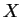 tem distribuição Gama com parâmetros
tem distribuição Gama com parâmetros 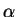 e
e 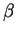 ,
denotando-se
,
denotando-se
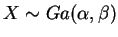 , se sua função de
densidade é dada por
para
, se sua função de
densidade é dada por
para
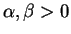 .
.
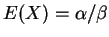
e
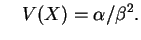
Casos particulares da distribuição Gama são a
distribuição de Erlang,
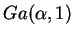 , a distribuição exponencial,
, a distribuição exponencial,
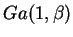 , e a distribuição qui-quadrado com
, e a distribuição qui-quadrado com 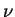 graus de
liberdade,
graus de
liberdade,
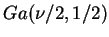 .
.
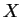 tem distribuição Gama Inversa com parâmetros
tem distribuição Gama Inversa com parâmetros 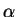 e
e 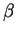 ,
denotando-se
,
denotando-se
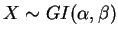 , se sua função de
densidade é dada por
para
, se sua função de
densidade é dada por
para
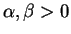 .
.
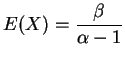
e
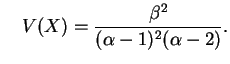
Não é difícil verificar que esta é a distribuição de 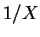 quando
quando
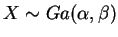 .
.
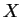 tem distribuição Beta com parâmetros
tem distribuição Beta com parâmetros 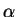 e
e 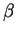 ,
denotando-se
,
denotando-se
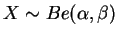 , se sua função de
densidade é dada por
para
, se sua função de
densidade é dada por
para
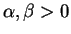 .
.
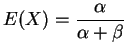
e
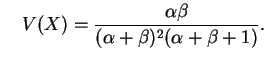
O vetor aleatório
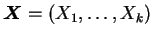 tem distribuição de
Dirichlet com parâmetros
tem distribuição de
Dirichlet com parâmetros
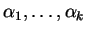 , denotada por
, denotada por
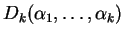 se sua função de
densidade conjunta é dada por
para
se sua função de
densidade conjunta é dada por
para
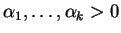 e
e
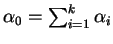 .
.
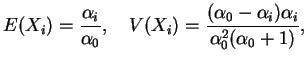
e
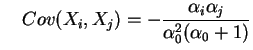
Note que a distribuição Beta é obtida como caso particular para 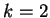 .
.
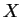 tem distribuição
tem distribuição 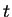 de Student (ou simplesmente
de Student (ou simplesmente 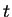 ) com média
) com média
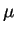 , parâmetro de escala
, parâmetro de escala 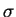 e
e 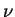 graus de liberdade,
denotando-se
graus de liberdade,
denotando-se
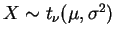 , se sua função de
densidade é dada por
para
, se sua função de
densidade é dada por
para 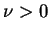 ,
,
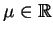 e
e 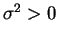 .
Um caso particular da distribuição
.
Um caso particular da distribuição 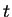 é a distribuição
de Cauchy, denotada por
é a distribuição
de Cauchy, denotada por 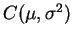 , que corresponde a
, que corresponde a 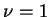 .
.
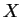 tem distribuição
tem distribuição 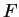 com
com 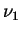 e
e 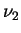 graus de liberdade,
denotando-se
graus de liberdade,
denotando-se
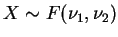 , se sua função de
densidade é dada por
, se sua função de
densidade é dada por
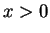 , e para
, e para
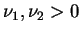 .
.
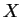 tem distribuição binomial com parâmetros
tem distribuição binomial com parâmetros 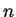 e
e 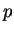 ,
denotando-se
,
denotando-se
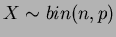 , se sua função de
probabilidade é dada por
para
, se sua função de
probabilidade é dada por
para 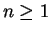 e
e 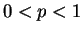 .
.
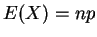
e
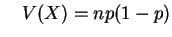
e um caso particular é a distribuição de Bernoulli com 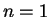 .
.
O vetor aleatório
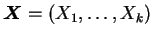 tem distribuição
multinomial com parâmetros
tem distribuição
multinomial com parâmetros 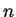 e probabilidades
e probabilidades
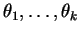 , denotada por
, denotada por
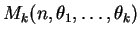 se sua função de
probabilidade conjunta é dada por
para
se sua função de
probabilidade conjunta é dada por
para
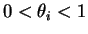 e
e
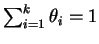 . Note que a
distribuição binomial é um caso especial da multinomial quando
. Note que a
distribuição binomial é um caso especial da multinomial quando
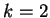 . Além disso, a distribuição marginal de cada
. Além disso, a distribuição marginal de cada 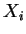 é binomial
com parâmetros
é binomial
com parâmetros 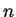 e
e 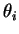 e
e
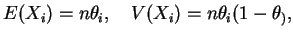
e
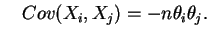
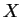 tem distribuição de Poisson com parâmetro
tem distribuição de Poisson com parâmetro 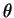 ,
denotando-se
,
denotando-se
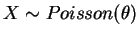 , se sua função de
probabilidade é dada por
para
, se sua função de
probabilidade é dada por
para 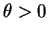 .
.
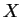 tem distribuição de binomial negativa com parâmetros
tem distribuição de binomial negativa com parâmetros 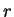 e
e 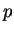 ,
denotando-se
,
denotando-se
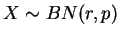 , se sua função de
probabilidade é dada por
para
, se sua função de
probabilidade é dada por
para 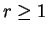 e
e 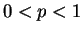 .
.
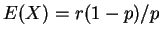
e
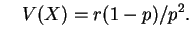



Next: Referências Bibliográficas
Up: CE-210 Inferência Estatística II
Previous: 2. Testes de Hipóteses
Sumário
Ricardo Ehlers & Paulo Justiniano
![]() tem distribuição normal multivariada com vetor
de médias
tem distribuição normal multivariada com vetor
de médias ![]() e matriz de variância-covariância
e matriz de variância-covariância ![]() ,
denotando-se
,
denotando-se
![]() se sua função de
densidade é dada por
se sua função de
densidade é dada por
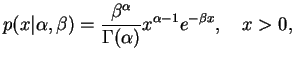
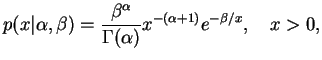
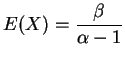 e
e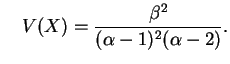
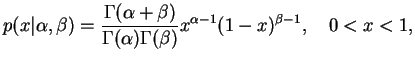
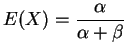 e
e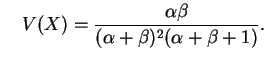
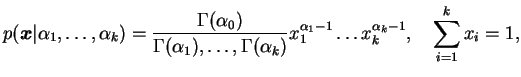
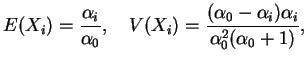 e
e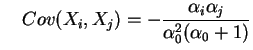
![$\displaystyle p(x\vert\nu,\mu,\s)=
\frac{\Gamma((\nu+1)/2)\nu^{\nu/2}}{\Gamma(\...
...igma}
\left[\nu+\frac{(x-\mu)^2}{\s}\right]^{-(\nu+1)/2},\quad x\in\mathbb{R},
$](img531.png)
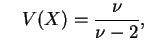 para
para 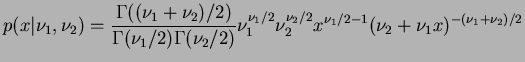
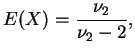 para
para 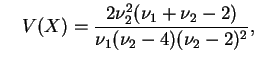 para
para