A principal restrição da estimação pontual é que quando estimamos um parâmetro através de um único valor numérico toda a informação presente nos dados é resumida através deste número. É importante encontrar também um intervalo de valores plausíveis para o parâmetro.
A idéia é construir um intervalo em torno da estimativa pontual de modo que ele tenha uma probabilidade conhecida de conter o verdadeiro valor do parâmetro. Tipicamente as distribuições amostrais de estimadores dos parâmetros desconhecidos serão utilizadas. Antes de descrever o procedimento geral veremos um exemplo simples de construção do intervalo de confiança.
Seja
![]() uma amostra aleatória
da distribuição
uma amostra aleatória
da distribuição
![]() , com
, com ![]() conhecido. Para fazer inferências sobre
conhecido. Para fazer inferências sobre
![]() nos baseamos na média amostral
nos baseamos na média amostral
![]() e sabemos
que
e sabemos
que
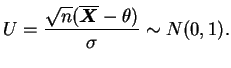
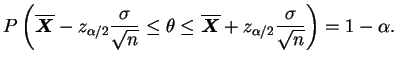
Esta última igualdade pode dar margem a interpretações errôneas, o que
aliás acontece com bastante frequência. O parâmetro ![]() é
desconhecido mas fixo e portanto não é passível de descrição
probabilística, ou seja não se trata de um intervalo de probabilidade
para
é
desconhecido mas fixo e portanto não é passível de descrição
probabilística, ou seja não se trata de um intervalo de probabilidade
para ![]() . Na verdade os limites do intervalo é que são variáveis
aleatórias e após a amostra ser observada dizemos que
. Na verdade os limites do intervalo é que são variáveis
aleatórias e após a amostra ser observada dizemos que
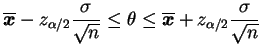
Vale notar também que, para um dado valor de ![]() , é possível
construir muitos intervalos de confiança diferentes para
, é possível
construir muitos intervalos de confiança diferentes para ![]() . Na
verdade, quaisquer constantes
. Na
verdade, quaisquer constantes ![]() e
e ![]() tais que
tais que
![]() podem ser usadas para construir um
intervalo com limites
podem ser usadas para construir um
intervalo com limites
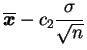 e
e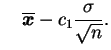
O procedimento geral para construção de intervalos de confiança consiste nos seguintes passos,
A exigência de que a probabilidade no item 2 acima possa ser maior do que o nível de confiança é essencialmente técnica pois queremos que o intervalo seja o menor possível, o que em geral implica em usar uma igualdade. A desigualdade será útil principalmente no caso de distribuições discretas onde nem sempre é possível satisfazer a igualdade.
Note que a variável aleatória ![]() , comumente denominada quantidade
pivotal ou pivot, é fundamental para o funcionamento do
método. Idealmente ela deve depender da amostra através de
estatísticas suficientes minimais e ter distribuição conhecida.
, comumente denominada quantidade
pivotal ou pivot, é fundamental para o funcionamento do
método. Idealmente ela deve depender da amostra através de
estatísticas suficientes minimais e ter distribuição conhecida.
É importante notar também que este intervalo não pode ser
interpretado como
um intervalo de probabilidade para ![]() já que a aleatoriedade
presente é devida a amostra
já que a aleatoriedade
presente é devida a amostra ![]() . Ou seja, o procedimento leva a
construção de um intervalo probabilístico para
. Ou seja, o procedimento leva a
construção de um intervalo probabilístico para ![]() e não para
e não para ![]() .
.
Tecnicamente, dizemos que
![]() de todos os intervalos de confiança que
construirmos conterão o verdadeiro valor do parâmetro (dado que todas
as suposições envolvidas estejam corretas). Por exemplo se
de todos os intervalos de confiança que
construirmos conterão o verdadeiro valor do parâmetro (dado que todas
as suposições envolvidas estejam corretas). Por exemplo se
![]() então, em média, somente 5 a cada 100 intervalos não
conterão
então, em média, somente 5 a cada 100 intervalos não
conterão ![]() . A probabilidade
. A probabilidade ![]() é denominada nível de
confiança e sua
escolha depende da precisão com que queremos
estimar o parâmetro, sendo que 0,90, 0,95 e 0,99 são os valores mais
comuns na prática.
é denominada nível de
confiança e sua
escolha depende da precisão com que queremos
estimar o parâmetro, sendo que 0,90, 0,95 e 0,99 são os valores mais
comuns na prática.
Nesta seção serão discutidos os casos em que os dados provém de uma distribuição normal. Inicialmente veremos o caso em que temos uma única amostra de uma distribuição normal e queremos estimar sua média e sua variância. Na Seção 1.2.2 estudaremos o caso de duas amostras tomadas de distribuições normais independentes.
No exemplo 1..1, se ![]() for desconhecido não
podemos usar a mesma
quantidade pivotal já que ela depende de
for desconhecido não
podemos usar a mesma
quantidade pivotal já que ela depende de ![]() . Ou seja, precisamos
obter uma outra
quantidade pivotal que depende apenas de
. Ou seja, precisamos
obter uma outra
quantidade pivotal que depende apenas de ![]() e de
e de ![]() e com uma
distribuição que seja conhecida e não dependa de nenhum parâmetro
desconhecido. No modelo normal isto será possível usando os resultados
a seguir.
e com uma
distribuição que seja conhecida e não dependa de nenhum parâmetro
desconhecido. No modelo normal isto será possível usando os resultados
a seguir.
Seja
![]() uma amostra aleatória da distribuição
uma amostra aleatória da distribuição
![]() e sejam
e sejam
![]() e
e ![]() a média e a variância
amostrais. Então, condicionado em
a média e a variância
amostrais. Então, condicionado em ![]() e
e ![]() ,
,
![]() e
e
![]() são independentes com distribuições amostrais
são independentes com distribuições amostrais
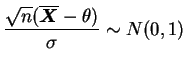 e
e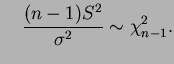
Se
![]() e
e
![]() e se
e se ![]() e
e ![]() são
independentes então
são
independentes então
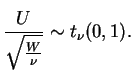
Seja
![]() uma amostra aleatória da distribuição
uma amostra aleatória da distribuição
![]() e sejam
e sejam
![]() e
e ![]() a média e a variância
amostrais. Então, condicionado em
a média e a variância
amostrais. Então, condicionado em ![]() e
e ![]() ,
,
![]() tem distribuição amostral
tem distribuição amostral
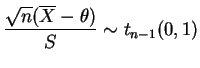
Estes resultados nos permitem definir quantidades pivotais para
construção de intervalos de confiança para ![]() e
e ![]() . No caso da
média
. No caso da
média ![]() , o valor desconhecido de
, o valor desconhecido de ![]() é substituido pelo
seu estimador
é substituido pelo
seu estimador ![]() levando a uma quantidade pivotal com distribuição
levando a uma quantidade pivotal com distribuição
![]() com
com ![]() graus de liberdade. Assim, podemos obter o percentil
graus de liberdade. Assim, podemos obter o percentil
![]() tal que
tal que
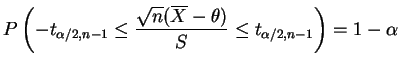
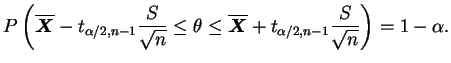
Finalmente, após observar a amostra substituimos as estimativas e dizemos que
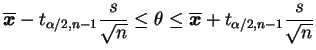
Para obter estimativas da variância populacional ![]() usamos uma
quantidade pivotal com distribuição qui-quadrado com
usamos uma
quantidade pivotal com distribuição qui-quadrado com ![]() graus de
liberdade. Devemos então obter os percentis
graus de
liberdade. Devemos então obter os percentis
![]() e
e
![]() desta distribuição tais que
desta distribuição tais que
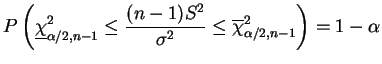
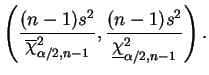
Nesta seção vamos assumir que
![]() e
e
![]() são
amostras aleatórias das distribuições
são
amostras aleatórias das distribuições
![]() e
e
![]() respectivamente e que as amostras são independentes.
respectivamente e que as amostras são independentes.
Podemos comparar as médias populacionais estimando a diferença
![]() . A estimação é baseada na diferença entre
médias amostrais, i.e.
. A estimação é baseada na diferença entre
médias amostrais, i.e.
![]() que é o
estimador de máxima verossimilhança de
que é o
estimador de máxima verossimilhança de ![]() . Se as variâncias
populacionais forem conhecidas então a distribuição amostral é dada
por
. Se as variâncias
populacionais forem conhecidas então a distribuição amostral é dada
por
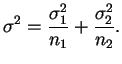
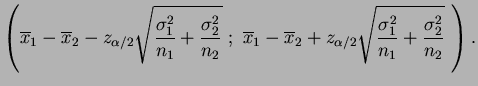
No caso de variâncias populacionais desconhecidas porém iguais,
i.e.
![]() podemos combinar os duas variâncias amostrais para formar uma
estimativa combinada da variância. Atribuímos mais peso às
amostras maiores e esta variância combinada é dada por
podemos combinar os duas variâncias amostrais para formar uma
estimativa combinada da variância. Atribuímos mais peso às
amostras maiores e esta variância combinada é dada por
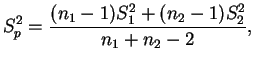
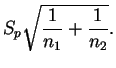
Do exposto acima, um intervalo de confiança para a diferença entre
médias
![]() assumindo desvios padrão iguais pode ser
construído usando-se a quantidade pivotal
assumindo desvios padrão iguais pode ser
construído usando-se a quantidade pivotal
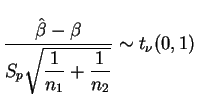
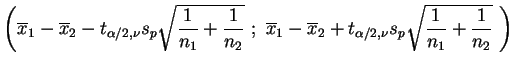
Analogamente ao caso de uma amostra, o intervalo de confiança para
![]() é construído usando-se a quantidade pivotal
é construído usando-se a quantidade pivotal
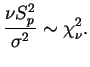
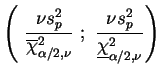
Até agora assumimos que as variâncias populacionais desconhecidas eram
iguais (ou pelo menos aproximadamente iguais). A violação desta
suposição leva a problemas teóricos e práticos uma vez que não é
trivial encontrar uma quantidade pivotal para ![]() com distribuição
conhecida. Na verdade, se existem grandes diferenças de variabilidade
entre as duas populações pode ser mais apropriado analisar
conjuntamente as consequências das diferenças entre as médias e as
variâncias. Assim, caso o pesquisador tenha interesse no parâmetro
com distribuição
conhecida. Na verdade, se existem grandes diferenças de variabilidade
entre as duas populações pode ser mais apropriado analisar
conjuntamente as consequências das diferenças entre as médias e as
variâncias. Assim, caso o pesquisador tenha interesse no parâmetro
![]() deve levar em conta os problemas de ordem teóricas
introduzidos por uma diferença substancial entre
deve levar em conta os problemas de ordem teóricas
introduzidos por uma diferença substancial entre ![]() e
e ![]() .
.
A literatura estatística apresenta vários métodos para resolver este problema mas nenhum deles é completamente satisfatório. Um procedimento possível consiste em utilizar a estatística
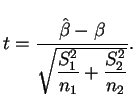
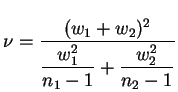
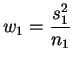 e
e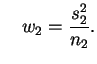
Outra situação de interesse é a comparação das duas variâncias populacionais. Neste caso, faz mais sentido utilizar a razão de variâncias ao invés da diferença já que elas medem a escala de uma distribuição e são sempre positivas. Para obter a distribuição amostral apropriada usaremos o teorema a seguir.
Sejam as variáveis aleatórias ![]() e
e ![]() independentes com
distribuições qui-quadrado com
independentes com
distribuições qui-quadrado com ![]() e
e ![]() graus de liberdade
respectivamente. Então a variável aleatória dada por
graus de liberdade
respectivamente. Então a variável aleatória dada por
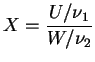
Usaremos a notação
![]() e dos teoremas 1.1 e
1.2 não é difícil mostrar que
e dos teoremas 1.1 e
1.2 não é difícil mostrar que
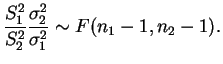
Embora sua função de distribuição não possa ser obtida analiticamente os valores estão tabelados em muitos livros de estatística e também podem ser obtidos na maioria dos pacotes computacionais. Os percentis podem então ser utilizados na construção de intervalos de confiança para a razão de variâncias.
Uma propriedade bastante útil para calcular probabilidade com a
distribuição ![]() vem do fato de que se
vem do fato de que se
![]() então
então
![]() por simples inversão na razão de
distribuições qui-quadrado independentes. Assim, denotando os quantis
por simples inversão na razão de
distribuições qui-quadrado independentes. Assim, denotando os quantis
![]() e
e ![]() da distribuição
da distribuição
![]() por
por
![]() e
e
![]() respectivamente segue que
respectivamente segue que
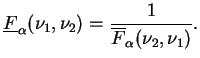
Seja
![]() uma amostra aleatória de uma distribuição de
Bernoulli com parâmetro
uma amostra aleatória de uma distribuição de
Bernoulli com parâmetro ![]() . Assim,
. Assim,
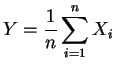
Pelo teorema central do limite, para ![]() grande e
grande e ![]() não muito
próximo de 0 ou 1, a distribuição de
não muito
próximo de 0 ou 1, a distribuição de ![]() será
aproximadamente normal com média
será
aproximadamente normal com média ![]() e um desvio
padrão dado por
e um desvio
padrão dado por
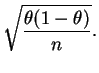
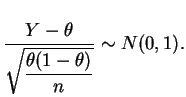
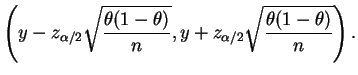
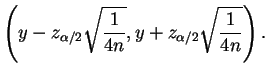
No entanto, se o verdadeiro valor de ![]() estiver afastado do seu
valor máximo e estiver próximo de 0 ou de 1 então este intervalo tem
amplitude desnecessariamente grande porque substituimos
estiver afastado do seu
valor máximo e estiver próximo de 0 ou de 1 então este intervalo tem
amplitude desnecessariamente grande porque substituimos
![]() pelo seu valor máximo. Um enfoque mais otimista
consiste em substituir
pelo seu valor máximo. Um enfoque mais otimista
consiste em substituir ![]() pela sua estimativa de máxima
verossimilhança, i.e. a proporção amostral de sucessos
pela sua estimativa de máxima
verossimilhança, i.e. a proporção amostral de sucessos ![]() e utilizar
o intervalo
e utilizar
o intervalo
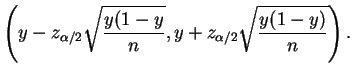
Note que, para ![]() e
e ![]() fixos a amplitude do intervalo conservativo será a
mesma para todas as possíveis amostras de tamanho
fixos a amplitude do intervalo conservativo será a
mesma para todas as possíveis amostras de tamanho ![]() . Por outro lado,
usando-se esta última expressão o intervalo terá amplitude
. Por outro lado,
usando-se esta última expressão o intervalo terá amplitude
![]() que varia de amostra para amostra.
que varia de amostra para amostra.
Utilizando os conceitos do método da quantidade pivotal e a propriedade
de normalidade assintótica dos estimadores de máxima verossimilhança
podemos construir intervalos de confiança para ![]() . Antes porém
precisamos da definição da medida de informação de Fisher.
. Antes porém
precisamos da definição da medida de informação de Fisher.
Considere uma única observação ![]() com função de
(densidade) de probabilidade
com função de
(densidade) de probabilidade
![]() . A medida de informação
esperada de Fisher de
. A medida de informação
esperada de Fisher de ![]() através de
através de ![]() é definida como
é definida como
![$\displaystyle I(\theta)=E \left[-\frac{\partial^2\log
p(x\vert\theta)}{\partial\theta^2}\right].
$](img118.png)
![$\displaystyle \bfI(\btheta)= E \left[-\frac{\partial^2\log
p(x\vert\btheta)}{\partial\btheta\partial\btheta'} \right].
$](img121.png)
Note que o conceito de informação aqui está sendo associado a uma
espécie de
curvatura média da função de verossimilhança no sentido de que quanto
maior a curvatura mais precisa é a informação contida na
verossimilhança, ou equivalentemente maior o valor de
![]() . Em geral espera-se que a curvatura seja negativa e por
isso seu valor é tomado com sinal trocado. Note também que a esperança
matemática é tomada em relação à distribuição amostral
. Em geral espera-se que a curvatura seja negativa e por
isso seu valor é tomado com sinal trocado. Note também que a esperança
matemática é tomada em relação à distribuição amostral
![]() .
.
Podemos considerar então ![]() uma medida de informação
global enquanto que uma medida de informação local é obtida quando não
se toma o valor
esperado na definição acima. A medida de informação observada de
Fisher
uma medida de informação
global enquanto que uma medida de informação local é obtida quando não
se toma o valor
esperado na definição acima. A medida de informação observada de
Fisher ![]() fica então definida como
fica então definida como
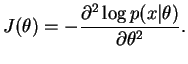
Seja
![]() uma coleção de variáveis aleatórias
independentes com distribuições
uma coleção de variáveis aleatórias
independentes com distribuições
![]() ,
,
![]() e
sejam
e
sejam ![]() e
e
![]() as medidas de informação de
as medidas de informação de
![]() obtidas através de
obtidas através de ![]() e de
e de ![]() ,
respectivamente. Então,
,
respectivamente. Então,
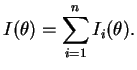
O lema nos diz então que a informação total contida em observações
independentes é igual a soma das informações individuais. Um caso
particular importante é quando as observações são também identicamente
distribuidas já que neste caso
![]() é constante e assim a
informação total é simplesmente
é constante e assim a
informação total é simplesmente
![]() .
.
Outra estatística importante no estudo da função de verossimilhança e
que será útil na construção de intervalos de confiança assintóticos é
a função escore.
A função escore de ![]() denotada por
denotada por
![]() é dada
por
é dada
por
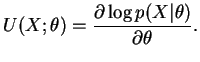
Além disso, pode-se mostrar que o valor esperado da função
escore é zero e sua variância é dada por ![]() .
.
Vimos em estimação pontual que, para grandes amostras, o estimador de máxima
verossimilhança
![]() para um parâmetro
para um parâmetro ![]() tem
distribuição aproximadamente normal com média
tem
distribuição aproximadamente normal com média ![]() sob condições
de regularidade gerais. Assim, mesmo que
sob condições
de regularidade gerais. Assim, mesmo que
![]() seja viesado
para
seja viesado
para ![]() fixo ele será assintoticamente não viesado. A variância
assintótica é dada por
fixo ele será assintoticamente não viesado. A variância
assintótica é dada por
![]() . Ou seja, para
. Ou seja, para ![]() grande
grande
![]() tem distribuição aproximadamente
tem distribuição aproximadamente
![]() e podemos construir intervalos de
confiança aproximados para
e podemos construir intervalos de
confiança aproximados para ![]() . Neste caso,
. Neste caso,
![]() pode ser tratado como uma
quantidade pivotal aproximada e se for possível isolar
pode ser tratado como uma
quantidade pivotal aproximada e se for possível isolar ![]() na
desigualdade
na
desigualdade
Seja
![]() uma amostra aleatória da distribuição
exponencial com parâmetro
uma amostra aleatória da distribuição
exponencial com parâmetro ![]() . A função de densidade conjunta é
dada por
. A função de densidade conjunta é
dada por
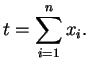
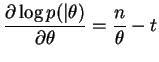 e
e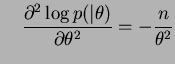
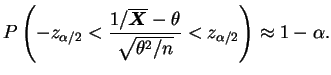
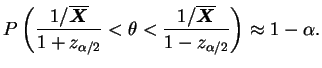
Um fato importante é que, em geral, na distribuição assintótica normal
do estimador de máxima verossimilhança a sua variância
![]() pode ser
substituida pelo seu estimador
pode ser
substituida pelo seu estimador
![]() sem afetar muito
a acurácia da aproximação. Este fato, que não será provado aqui,
simplifica bastante a conversão das desigualdades para obtenção
de intervalos de confiança aproximados. Assim,
sem afetar muito
a acurácia da aproximação. Este fato, que não será provado aqui,
simplifica bastante a conversão das desigualdades para obtenção
de intervalos de confiança aproximados. Assim,
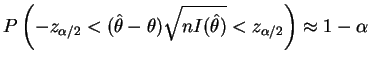
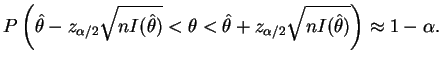
Em algumas situações não se tem uma forma explícita para o estimador
de máxima verossimilhança e neste caso a função escore será
particularmente útil. Lembrando que a função escore de ![]() tem média
zero e variância igual a
tem média
zero e variância igual a ![]() então temos pelo
teorema central do limite que
então temos pelo
teorema central do limite que
![]() converge em
distribuição para uma
converge em
distribuição para uma
![]() . Podemos usar este resultado
para fazer inferência aproximada sobre
. Podemos usar este resultado
para fazer inferência aproximada sobre ![]() e assim o intervalo de
confiança aproximado de
e assim o intervalo de
confiança aproximado de
![]() é obtido fazendo-se
é obtido fazendo-se
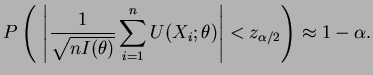
Finalmente, vale ressaltar que todos os resultados desta seção podem
ser extendidos para o caso de
um vetor paramétrico
![]() . Neste caso,
a distribuição assintótica do estimador de máxima verossimilhança
será normal multivariada com vetor de médias
. Neste caso,
a distribuição assintótica do estimador de máxima verossimilhança
será normal multivariada com vetor de médias ![]() e matriz de
variância-covariância igual a
e matriz de
variância-covariância igual a
![]() onde
onde
![]() é a matriz de informação de Fisher.
é a matriz de informação de Fisher.