Next: 9 Miscelânia de funcionalidades Up: Curso sobre o programa Previous: 7 Conceitos básicos sobre
Agora que já nos familiarizamos com o uso das distribuições de probabilidade vamos ver alguns detalhes adicionais sobre seu funcionamento.
A probabilidade de um evento em uma distribuição contínua é uma área sob a curva da distribuição. Vamos reforçar esta idéia revisitando um exemplo visto na aula anterior.
Seja ![]() uma v.a. com distribuição
uma v.a. com distribuição ![]() .
Para calcular a probabilidade
.
Para calcular a probabilidade
![]() usamos o comando:
usamos o comando:
> pnorm(95, 100, 10) [1] 0.3085375
Vamos agora ``esquecer'' o comando pnorm
e ver uma outra forma de resolver usando integração numérica.
Lembrando que a normal tem a função de densidade dada por
fn <- function(x){
fx <- (1/sqrt(2*pi*100)) * exp((-1/200) * (x - 100)^2)
return(fx)
}
Para obter o gráfico desta distribuição mostrado na Figura ![[*]](crossref.png) usamos o fato que
a maior parte da função está no intervalo entre a média +/- três desvios padrões, portanto entre 70 e 130.
Podemos então fazer:
usamos o fato que
a maior parte da função está no intervalo entre a média +/- três desvios padrões, portanto entre 70 e 130.
Podemos então fazer:
x <- seq(70, 130, l=200) fx <- fn(x) plot(x, fx, type='l')Agora vamos marcar no gráfico a área que corresponde a probabilidade pedida. Para isto vamos criar um polígono com coordenadas
ax e ay definindo o perímetro
desta área
ax <- c(70, 70, x[x<95], 95,95) ay <- c(0, fn(70), fx[x<95], fn(95),0) polygon(ax,ay, dens=10)Para calcular a área pedida sem usar a função
pnorm
podemos usar a função de integração numérica. Note que esta função, diferentemente da pnorm reporta ainda o erro de aproximação numérica.
integrate(fn, -Inf, 95) 0.3085375 with absolute error < 2.1e-06Portanto para os demais ítens do problema
> integrate(fn, 90, 110) 0.6826895 with absolute error < 7.6e-15 > integrate(fn, 95, +Inf) 0.6914625 with absolute error < 8.1e-05e os resultados acima evidentemente coincidem com os obtidos na aula anterior usando
pnorm.
Note ainda que na prática não precisamos definir e usar a função ![]() pois ela fornece o mesmo resultado que a função
pois ela fornece o mesmo resultado que a função dnorm.
A função de densidade de probabilidade da distribuição exponencial com parâmetro ![]() e denotada
e denotada ![]() é dada por:
é dada por:
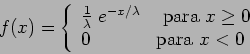
Seja uma variável ![]() com distribuição exponencial de parâmetro
com distribuição exponencial de parâmetro ![]() .
Calcular a probabilidade
.
Calcular a probabilidade ![]() .
.
A solução analítica pode ser encontrada resolvendo
Para ilustrar o uso do R vamos também obter a resposta usando integração numérica. Para isto vamos criar uma função com a expressão da exponencial e depois integrar no intervalo pedido
> fexp <- function(x, lambda=500){
fx <- ifelse(x<0, 0, (1/lambda)*exp(-x/lambda))
return(fx)
}
> integrate(fexp, 400, Inf)
0.449329 with absolute error < 5e-06
e este resultado deve ser igual ao encontrado com a solução analítica.
Note ainda que poderíamos obter o mesmo resultado simplesmente usando a função pexp
com o comando pexp(400, rate=1/500, lower=F),
onde o argumento corresponde a ![]() na equação da exponencial.
na equação da exponencial.
A Figura ![[*]](crossref.png) mostra o gráfico desta distribuição com indicação da área correspondente à probabilidade pedida. Note que a função é positiva no intervalo
mostra o gráfico desta distribuição com indicação da área correspondente à probabilidade pedida. Note que a função é positiva no intervalo ![]() mas para fazer o gráfico consideramos apenas o intervalo
mas para fazer o gráfico consideramos apenas o intervalo ![]() .
.
x <- seq(0,2000, l=200) fx <- dexp(x, rate=1/500) plot(x, fx, type='l') ax <- c(400, 400, x[x>400], 2000,2000) ay <- c(0, dexp(c(400,x[x>400], 2000), 1/500),0) polygon(ax,ay, dens=10)
Sabemos que para a distribuição exponencial a esperança
![]() e a variância
e a variância
![]() pois podem ser obtidos analiticamente.
pois podem ser obtidos analiticamente.
Novamente para ilustrar o uso do R vamos ``esquecer'' que conhecemos estes resultados e vamos obtê-los numericamente. Para isto vamos definir funções para a esperança e variância e fazer a integração numérica.
e.exp <- function(x, lambda = 500){
ex <- x * (1/lambda) * exp(-x/lambda)
return(ex)
}
> integrate(e.exp, 0, Inf)
500 with absolute error < 0.00088
> ex <- integrate(e.exp, 0, Inf)$value
> ex
[1] 500
v.exp <- function(x, lambda = 500, exp.x){
vx <- ((x-exp.x)^2) * (1/lambda) * exp(-x/lambda)
return(vx)
}
> integrate(v.exp, 0, Inf, exp.x=ex)
250000 with absolute error < 6.9
A geração da amostra depende de um gerador de números aleatórios que é controlado por uma semente (seed em inglês). Cada vez que o comando rnorm é chamado diferentes elementos da amostra são produzidos, porque a semente do gerador é automaticamente modificada pela função. Em geral o usuário não precisa se preocupar com este mecanismo. Mas caso necessário a função set.seed pode ser usada para controlar o comportamento do gerador de números aleatórios. Esta função define o valor inicial da semente que é mudado a cada geração subsequente de números aleatórios. Portanto para gerar duas amostras idênticas basta usar o comando set.seed conforme ilustrado abaixo.
> set.seed(214) # define o valor da semente > rnorm(5) # amostra de 5 elementos [1] -0.46774980 0.04088223 1.00335193 2.02522505 0.30640096 > rnorm(5) # outra amostra de 5 elementos [1] 0.4257775 0.7488927 0.4464515 -2.2051418 1.9818137 > set.seed(214) # retorna o valor da semente ao valor inicial > rnorm(5) # gera novamente a primeira amostra de 5 elementos [1] -0.46774980 0.04088223 1.00335193 2.02522505 0.30640096No comando acima mostramos que depois da primeira amostra ser retirada a semente é mudada e por isto os elementos da segunda amostra são diferentes dos da primeira. Depois retornamos a semente ao seu estado original a a próxima amostra tem portanto os mesmos elementos da primeira.
Para saber mais sobre geração de números aleatórios no R veja
help(.Random.seed) e help(set.seed)
> qnorm(c(0.05, 0.95)) [1] -1.644854 1.644854 > rnorm(4, mean=c(0, 10, 100, 1000)) [1] 0.1599628 9.0957340 100.5595095 999.9129392 > rnorm(4, mean=c(10, 20, 30, 40), sd=c(2, 5)) [1] 10.58318 21.92976 29.62843 42.71741Note que no último exemplo a lei da reciclagem foi utilizada no vetor de desvios padrão, i.e. os desvios padrão utilizados foram
Nos livros texto de estatística voce vai ver que as distribuições binomial e Poisson podem ser aproximadas pela normal. Isto significa que podemos usar a distribuição normal para calcular probabilidades aproximadas em casos em que seria ``trabalhoso'' calcular as probabilidades exatas pala binomial ou Poisson. Isto é especialmente importante no caso de usarmos calculadoras e/ou tabelas para calcular probabilidades. Quando usamos um computador esta aproximação é menos importante, visto que é fácil calcular as probabilidades exatas com o auxílio do computador. De toda forma vamos ilustrar aqui este resultado.
Vejamos como fica a aproximação no caso da distribuição binomial.
Seja
![]() . Na prática, em geral a aproximação é considerada aceitável
quando
. Na prática, em geral a aproximação é considerada aceitável
quando ![]() e
e ![]() e sendo tanto melhor quanto maior for o valor de
e sendo tanto melhor quanto maior for o valor de ![]() .
A aproximação neste caso é de que
.
A aproximação neste caso é de que
![]() .
.
Seja
![]() e portanto com a aproximação
e portanto com a aproximação
![]() .
A Figura
.
A Figura ![[*]](crossref.png) mostra o gráfico da distribuição binomial e da aproximação pela normal.
mostra o gráfico da distribuição binomial e da aproximação pela normal.
xb <- 0:10 px <- dbinom(xb, 10, 0.5) plot(xb, px, type='h') xn <- seq(0, 10, len=100) fx <- dnorm(xn, 5, sqrt(2.5)) lines(xn, fx)
Vamos também calcular as seguintes probabilidades exatas e aproximadas, lembrando que ao usar a aproximação pela normal devemos usar a correção de continuidade e/ou somando e subtraindo 0.5 ao valor pedido.
> pbinom(5, 10, 0.5) [1] 0.6230469 > pnorm(5.5, 5, sqrt(2.5)) [1] 0.6240852
> pbinom(6, 10, 0.5) [1] 0.828125 > pnorm(6.5, 5, sqrt(2.5)) [1] 0.8286091
> 1-pbinom(2, 10, 0.5) [1] 0.9453125 > 1-pnorm(2.5, 5, sqrt(2.5)) [1] 0.9430769
> 1-pbinom(1, 10, 0.5) [1] 0.9892578 > 1-pnorm(1.5, 5, sqrt(2.5)) [1] 0.9865717
> dbinom(7, 10, 0.5) [1] 0.1171875 > pnorm(7.5, 5, sqrt(2.5)) - pnorm(6.5, 5, sqrt(2.5)) [1] 0.1144677
> pbinom(8, 10, 0.5) - pbinom(3, 10, 0.5) [1] 0.8173828 > pnorm(8.5, 5, sqrt(2.5)) - pnorm(3.5, 5, sqrt(2.5)) [1] 0.8151808
> pbinom(5, 10, 0.5) - pbinom(0, 10, 0.5) [1] 0.6220703 > pnorm(5.5, 5, sqrt(2.5)) - pnorm(0.5, 5, sqrt(2.5)) [1] 0.6218719