Next: 8 Complementos sobre distribuições Up: Curso sobre o programa Previous: 6 Distribuições de Probabilidade
Os problemas nesta sessão foram retirados do livro:
Bussab, W.O. & Morettin, P.A. Estatística Básica. ![]() edição. Atual Editora. 1987.
edição. Atual Editora. 1987.
EXEMPLO 1 (adaptado de Bussab & Morettin, página 132, exercício 1)
Dada a função
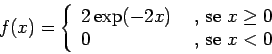
Para ser f.d.p. a função não deve ter valores negativos e deve
integrar 1 em seu domínio.
Vamos começar definindo esta função como uma função no R para qual daremos o nome de ![]() .
A seguir fazemos o gráfico da função.
Como a função tem valores positivos para
.
A seguir fazemos o gráfico da função.
Como a função tem valores positivos para ![]() no intervalo de zero a infinito
temos, na prática, para fazer o gráfico,
que definir um limite em
no intervalo de zero a infinito
temos, na prática, para fazer o gráfico,
que definir um limite em ![]() até onde vai o gráfico da função.
Vamos achar este limite tentando vários valores,
conforme mostram os comandos abaixo.
O gráfico escolhido foi o produzido pelo comando
até onde vai o gráfico da função.
Vamos achar este limite tentando vários valores,
conforme mostram os comandos abaixo.
O gráfico escolhido foi o produzido pelo comando plot(f1,0,5)
e mostrado na Figura ![[*]](crossref.png) .
.
f1 <- function(x){
fx <- ifelse(x < 0, 0, 2*exp(-2*x))
return(fx)
}
plot(f1)
plot(f1,0,10)
plot(f1,0,5)
Para verificar que a a integral da função é igual a 1 podemos usar a função integrate que efetua integração numérica.
A função recebe como argumentos o objeto com a função a ser integrada e os limites de integração.
Neste exemplo o objeto é f1 definido acima e o domínio da função é > integrate(f1, 0, Inf) 1 with absolute error < 5e-07
Para fazer cálculos pedidos nos itens (b) e (c) lembramos que a probabilidade é dada pela área sob a curva da função no intervalo pedido. Desta forma as soluções seriam dadas pelas expressões
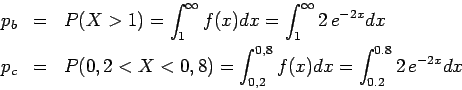
![[*]](crossref.png) .
Os comandos do R a seguir mostram como fazer o gráfico de função.
O comando
.
Os comandos do R a seguir mostram como fazer o gráfico de função.
O comando plot desenha o gráfico da função. Para destacar as áreas que correspondem às probabilidades pedidas vamos usar a função polygon. Esta função adiciona a um gráfico um polígono que é definido pelas coordenadas de seus vértices.
Para sombrear a área usa-se o argumento density.
Finalmente, para escrever um texto no gráfico usamos a função text
com as coordenadas de posição do texto.
> plot(f1,0,5) > polygon(x=c(1,seq(1,5,l=20)), y=c(0,f1(seq(1,5,l=20))), density=10) > polygon(x=c(0.2,seq(0.2,0.8,l=20),0.8), y=c(0,f1(seq(0.2,0.8,l=20)), 0), col="gray") > text(c(1.2, 0.5), c(0.1, 0.2), c(expression(p[b],p[c])))
e como obter as probabilidades pedidas.
> integrate(f1, 1, Inf) 0.1353353 with absolute error < 2.1e-05 > integrate(f1, 0.2, 0.8) 0.4684235 with absolute error < 5.2e-15
EXEMPLO 2 (Bussab & Morettin, página 139, exercício 10)
A demanda diária de arroz em um supermercado, em centenas de quilos, é uma v.a. ![]() com f.d.p.
com f.d.p.
![[*]](crossref.png) .
.
Neste caso definimos um vetor do mesmo tamanho do argumento x para armazenar os valores de ![]() e a seguir preenchemos os valores deste vetor para cada faixa de valor de
e a seguir preenchemos os valores deste vetor para cada faixa de valor de ![]() .
A seguir verificamos que a integral da função é 1 e fazemos o seu gráfico
mostrado na Figura
.
A seguir verificamos que a integral da função é 1 e fazemos o seu gráfico
mostrado na Figura ![[*]](crossref.png) .
.
> f2 <- function(x){
+ fx <- numeric(length(x))
+ fx[x < 0] <- 0
+ fx[x >= 0 & x < 1] <- 2*x[x >= 0 & x < 1]/3
+ fx[x >= 1 & x <= 3] <- (-x[x >= 1 & x <= 3]/3) + 1
+ fx[x > 3] <- 0
+ return(fx)
+ }
> integrate(f2, 0, 3) ## verificando que a integral vale 1
1 with absolute error < 1.1e-15
> plot(f2, -1, 4) ## fazendo o gráfico da função
Agora vamos responder às questões levantadas.
Na questão (a) pede-se a probabilidade de que sejam vendidos mais que 150 kg (1,5 centenas de quilos), portanto a probabilidade > integrate(f2, 1.5, Inf) 0.3749999 with absolute error < 3.5e-05A venda esperada em trinta dias é 30 vezes o valor esperado de venda em um dia. Para calcular a esperança
integrate retorna uma lista onde um dos elementos
($value) é o valor da integral.
## calculando a esperança da variável
> ef2 <- function(x){ x * f2(x) }
> integrate(ef2, 0, 3)
1.333333 with absolute error < 7.3e-05
> 30 * integrate(ef2, 0, 3)$value ## venda esperada em 30 dias
[1] 40
Na questão (c) estamos em busca do quantil 95% da distribuição de probabilidades, ou seja o valor de optimize do R, que recebe como argumentos a função a ser otimizada e o intervalo no qual deve procurar a solução. A resposta mostra o valor do quantil > f <- function(x) abs(0.95 - integrate(f2, 0, x)$value) > optimise(f, c(0,3)) $minimum [1] 2.452278 $objective [1] 7.573257e-08
A Figura ![[*]](crossref.png) ilustra as soluções dos itens (a) e (c)
e os comandos abaixo foram utilizados para obtenção destes gráficos.
ilustra as soluções dos itens (a) e (c)
e os comandos abaixo foram utilizados para obtenção destes gráficos.
par(mfrow=c(1,2), mar=c(3,3,0,0), mgp=c(2,1,0))
plot(f2, -1, 4)
polygon(x=c(1.5, 1.5, 3), y=c(0,f2(1.5),0), dens=10)
k <- optimise(f, c(0,3))$min
plot(f2, -1, 4)
polygon(x=c(0, 1, k, k), y=c(0,f2(1), f2(k), 0), dens=10)
text(c(1.5, k), c(0.2, 0), c("0.95", "k"), cex=2.5)
Finalmente lembramos que os exemplos discutidos aqui são simples e não requerem soluções numéricas, devendo ser resolvidos analiticamente. Utilizamos estes exemplos somente para ilustrar a obtenção de soluções numéricas com o uso do R, que na prática deve ser utilizado em problemas mais complexos onde soluções analíticas não são triviais ou mesmo impossíveis.