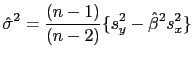Estimando os parâmetros do modelo

Uma tarefa importante associada com o modelo de regressão linear é a estimação dos valores de $\alpha$ e $\beta$, os quais juntos determinam a equação da reta ajustada.

Um método padrão de estimação em estatística chamado máxima verossimilhança leva às mesmas estimativas de mínimos quadrados descrito na seção anterior, ou seja

$$\hat{\beta} = s_{xy}/{s_x^2}$$   e$$\quad \quad \hat{\alpha} = \overline{y} - \hat{\beta} \overline{x}$$

Em aplicações, não existe garantia de que o modelo de regressão linear será razoável para nossos dados.

Devemos sempre sobrepor a reta ajustada $y = \hat{\alpha} + \hat{\beta} x$ sobre um scatterplot dos dados para checar se o modelo é razoável.

Devemos procurar por evidências de uma relação não-linear, ou desvios muito extremos da reta ajustada.

Se acharmos que o modelo está razoável, podemos também estimar $\sigma^2$, a variância dos erros $\varepsilon_i$, usando a fórmula

$$\hat{\sigma}^2 = \frac{(n-1)}{(n-2)}\{s^2_y - \hat{\beta}^2s^2_x\}$$

onde $s_y^2$ e $s_x^2$ denotam a variância amostral de $y$ e de $x$, respectivamente.