Exemplo

Para os nossos dados, já sabemos que $\hat{\alpha}=-51.17$ e que $\hat{\beta}=0.68$. Um gráfico dos dados com a reta ajustada é:

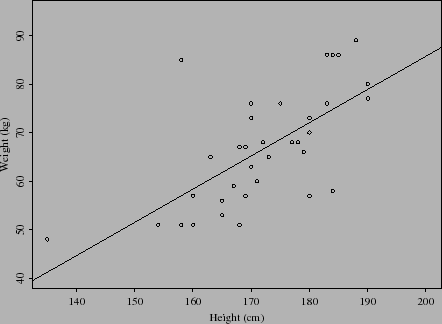
O ajuste da reta não parece tão bom. Existem dois pontos bem distantes da reta ajustada, e o da esquerda em particular parece ter uma grande influência na reta ajustada.

Na prática é aconselhavel investigar a acurácia destes valores e/ou verificar quanto muda a reta ajsutada quando estes pontos são removidos. Contudo, por enquanto prosseguiremos assumindo que está tudo ok!

Para sermos capazes de calcular erros padrão e intervalos de confiança, é importante manter tantas casa decimais quanto possível: $\hat{\beta}=0.6846253$.

As outras quantidades são:

$$n=37, \quad s_x = 11.38700, \quad s_y= 11.70791, \quad s_{xy} = 88.77102.$$

Podemos agora obter $\hat{\sigma}^2$:

$$\hat{\sigma}^2=\frac{36}{35}\{(11.70791^2)-(0.6846253^2) (11.38700^2)\}=78.48$$

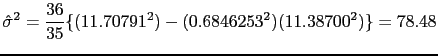
Então uma estimativa do desvio padrão dos desvios aleatórios $\varepsilon_i$ em torno da reta é

$$\hat{\sigma}=\sqrt{78.48}=8.86$$