Seguinte: Estimando os parâmetros do Acima: Regressão Anterior: Idéia básica
Este é o modelo mais simples para descrever a relação entre uma
variável explanatória ![]() e uma variável resposta
e uma variável resposta ![]() . O modelo faz a
seguintes suposições, em ordem decrescente de importância:
. O modelo faz a
seguintes suposições, em ordem decrescente de importância:
Em termos algébricos, seja ![]() para
para
![]() os
valores observados da variável explanatória
os
valores observados da variável explanatória ![]() e da variável resposta
e da variável resposta
![]() para os
para os ![]() sujeitos.
sujeitos.
O modelo de regressão linear é
Note que ![]() e
e ![]() são parâmetros da população, e eles
são frequentemente conhecidos como coeficientes. Em particular,
são parâmetros da população, e eles
são frequentemente conhecidos como coeficientes. Em particular,
![]() é denominado coeficiente, ou efeito, de
é denominado coeficiente, ou efeito, de ![]() .
.
Os dados abaixo parecem satisfazer todas as três suposições:
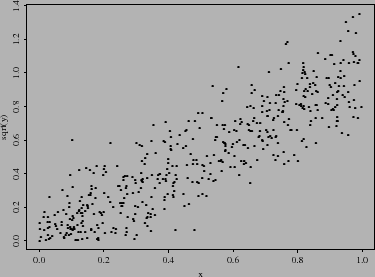
Um exemplo construído de dados que não satisfazem nenhuma das suposições é mostrado abaixo:
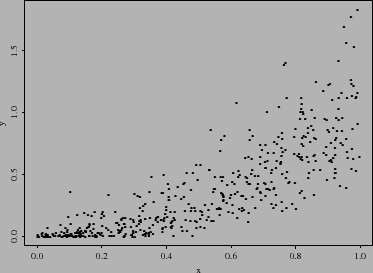
Silvia Shimakura 2011-04-04