Seguinte: Modelo de regressão linear Acima: Regressão Anterior: Regressão
Em certas situações podemos estar interessados em descrever a relação entre duas variáveis, e também predizer o valor de uma a partir de outra. Por exemplo, se sabemos a altura de um certo estudante, mas não o seu peso, qual seria um bom chute para o peso deste estudante? O coeficiente de correlação apenas indica a grau de associação como um único número.
Denote as alturas por
![]() , e os pesos por
, e os pesos por
![]() .
(Por enquanto vamos ignorar se eles são do sexo masculino ou
feminino).
.
(Por enquanto vamos ignorar se eles são do sexo masculino ou
feminino).
Se estamos interessados em predizer peso a partir de altura então não temos uma relação simétrica entre as duas variáveis. Chamamos peso a variável resposta ou dependente, e altura a variável explanatória, preditora ou independente.
A variável resposta é sempre disposta no eixo vertical ![]() , e a variável
explanatória é sempre disposta no eixo
, e a variável
explanatória é sempre disposta no eixo ![]() .
.
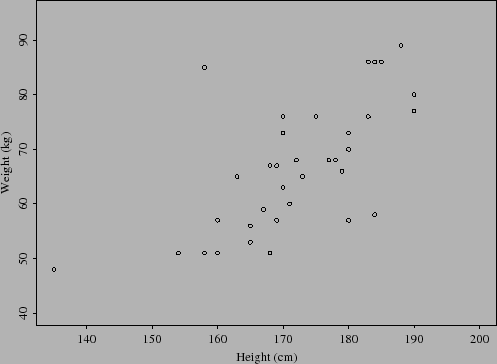
Se a relação entre as duas variáveis é aproximadamente linear, então os dados podem ser resumidos através do ajuste de uma reta passando pelos dados.
A equação dessa reta é dada por
Intuitivamente, queremos uma reta que forneça pequenas diferenças entre os verdadeiros pesos e aqueles dados pela reta para as alturas correspondentes.
O método padrão para obter a melhor reta ajustada é chamado
mínimos quadrados o qual literalmente miniza a soma dos
quadrados das distâncias de ![]() à reta ajustada.
à reta ajustada.
Em princípio isto requer traçar retas possíveis, calculando a soma dos quadrados das distâncias:
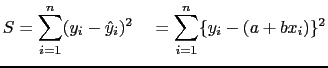
É possível mostrar que a melhor reta é aquela tal que
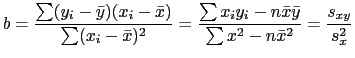
Nossos ![]() e
e ![]() são estimativas de
são estimativas de ![]() e
e ![]() . (É comum, denotar-se estas estimativas
por
. (É comum, denotar-se estas estimativas
por
![]() e
e
![]() ao invés de
ao invés de ![]() e
e ![]() .)
.)
O próximo passo é construir intervalos de confiança para ![]() e
e ![]() (intercepto e inclinação populacional), mas para fazer isto
precisamos pensar mais cuidadosamente sobre nossas suposições acerca
da população.
(intercepto e inclinação populacional), mas para fazer isto
precisamos pensar mais cuidadosamente sobre nossas suposições acerca
da população.
Silvia Shimakura 2011-04-04