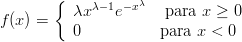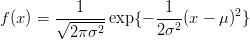
Agora que já nos familiarizamos com o uso das distribuições de probabilidade vamos ver alguns detalhes adicionais sobre seu funcionamento.
A probabilidade de um evento em uma distribuição contínua é uma área sob a curva da distribuição. Vamos reforçar esta idéia revisitando um exemplo visto na aula anterior.
Seja X uma v.a. com distribuição N(100, 100). Para calcular a probabilidade P[X < 95] usamos o comando:
Vamos agora “esquecer” o comando pnorm() e ver uma outra forma de resolver usando integração numérica. Lembrando que a normal tem a função de densidade dada por
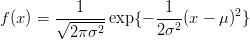
Para obter o gráfico desta distribuição mostrado na Figura 24 usamos o fato que a maior parte da função está no intervalo entre a média +/- três desvios padrões, portanto entre 70 e 130. Podemos então fazer como nos comandos que se seguem. Para marcar no gráfico a área que corresponde a probabilidade pedida criamos um polígono com coordenadas ax e ay definindo o perímetro desta área.
Para calcular a área pedida sem usar a função pnorm() podemos usar a função de integração numérica. Note que esta função, diferentemente da pnorm() reporta ainda o erro de aproximação numérica.
Portanto para os demais ítens do problema P[90 < X < 110] e P[X > 95] fazemos:
e os resultados acima evidentemente coincidem com os obtidos anterioriormente usando pnorm().
Note ainda que na prática não precisamos definir e usar a função fn pois ela fornece o mesmo resultado que a função dnorm().
A função de densidade de probabilidade da distribuição exponencial com parâmetro λ e denotada Exp(λ) é dada por:
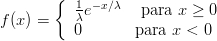
Seja uma variável X com distribuição exponencial de parâmetro λ = 500. Calcular a probabilidade P[X ≥ 400].
A solução analítica pode ser encontrada resolvendo
![∫ ∞ ∫ ∞ 1
P [X ≥ 400 ] = f(x)dx = --e-x∕λdx
400 400 λ](Rembrapa61x.png)
Para ilustrar o uso do R vamos também obter a resposta usando integração numérica. Para isto vamos criar uma função com a expressão da exponencial e depois integrar no intervalo pedido e este resultado deve ser igual ao encontrado com a solução analítica.
Note ainda que poderíamos obter o mesmo resultado simplesmente usando a função pexp() com o comando pexp(400, rate=1/500, lower=F), onde o argumento corresponde a 1∕λ na equação da exponencial.
A Figura 25 mostra o gráfico desta distribuição com indicação da área correspondente à probabilidade pedida. Note que a função é positiva no intervalo (0, +∞) mas para fazer o gráfico consideramos apenas o intervalo (0, 2000).
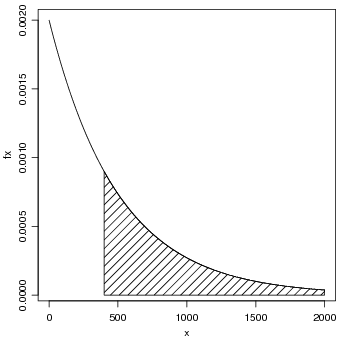
Sabemos que para a distribuição exponencial a esperança E[X] = ∫ 0∞xf(x)dx = λ e a variância V ar[X] = ∫ 0∞(x - E[X])2f(x)dx = λ2 pois podem ser obtidos analiticamente.
Novamente para ilustrar o uso do R vamos “esquecer” que conhecemos estes resultados e vamos obtê-los numericamente. Para isto vamos definir funções para a esperança e variância e fazer a integração numérica.
A geração da amostra depende de um gerador de números aleatórios que é controlado por uma semente (seed em inglês). Cada vez que o comando rnorm() é chamado diferentes elementos da amostra são produzidos, porque a semente do gerador é automaticamente modificada pela função. Em geral o usuário não precisa se preocupar com este mecanismo. Mas caso necessário set.seed() pode ser usada para controlar o comportamento do gerador de números aleatórios. Esta função define o valor inicial da semente que é mudado a cada geração subsequente de números aleatórios. Portanto para gerar duas amostras idênticas basta usar set.seed() conforme ilustrado abaixo.
Nos comandos acima mostramos que depois da primeira amostra ser retirada a semente é mudada e por isto os elementos da segunda amostra são diferentes dos da primeira. Depois retornamos a semente ao seu estado original a a próxima amostra tem portanto os mesmos elementos da primeira.
Para saber mais sobre geração de números aleatórios no R veja |help(.Random.seed)| e |help(set.seed)|
As funções de probabilidades aceitam também vetores em seus argumentos conforme ilustrado nos exemplo abaixo.
Note que no último exemplo a lei da reciclagem foi utilizada no vetor de desvios padrão, i.e. os desvios padrão utilizados foram (2, 5, 2, 5).
Nos livros texto de estatística podemos ver que as distribuições binomial e Poisson podem ser aproximadas pela normal. Isto significa que podemos usar a distribuição normal para calcular probabilidades aproximadas em casos em que seria “trabalhoso” calcular as probabilidades exatas pela binomial ou Poisson. Isto é especialmente importante no caso de usarmos calculadoras e/ou tabelas para calcular probabilidades. Quando usamos um computador esta aproximação é menos importante, visto que é fácil calcular as probabilidades exatas com o auxílio do computador. De toda forma vamos ilustrar aqui este resultado.
Vejamos como fica a aproximação no caso da distribuição binomial. Seja X ~ B(n,p). Na prática, em geral a aproximação é considerada aceitável quando np ≥ 5 e n(1 - p) ≥ 5 e sendo tanto melhor quanto maior for o valor de n. A aproximação neste caso é de que X ~ B(n,p) ≈ N(np,np(1 - p)).
Seja X ~ B(10, 1∕2) e portanto com a aproximação X ≈ N(5, 2.5). A Figura 26 mostra o gráfico da distribuição binomial e da aproximação pela normal.
Vamos também calcular as seguintes probabilidades exatas e aproximadas, lembrando que ao usar a aproximação pela normal devemos usar a correção de continuidade e/ou somando e subtraindo 0.5 ao valor pedido.