Capítulo 1 Modelos não lineares

Modelos de regressão são amplamente usados em diversas aplicações para descrever a relação entre uma variável resposta \(Y\) e uma variável explicativa \(x\). O modelo estatístico é linear se a quantidade de interesse, geralmente a média de \(Y\), é função linear dos parâmetros, caso contrário é não linear. Por exemplo, em estudos de adubação a produção média (ton) pode ser modelada como função quadrática da dose de um nutriente (kg) \[\begin{equation} \tag{1.1} f(x) = a + bx + cx^2. \end{equation}\] O modelo em (1.1) é linear nos parâmetros \(a\), \(b\) e \(c\). No entanto, a produção média também pode ser modelada pela lei de Mitscherlich \[\begin{equation} \tag{1.2} f(x) = a (1 - \exp\{-b(x - c)\}), \end{equation}\]

em que \(a\) (ton) representa a produção máxima teórica possível quando se aumenta indefinidamente a dose do nutriente, \(b\) (kg\(^{-1}\)) é interpretado como coeficiente de eficácia do nutriente, e \(c\) (kg) seria o conteúdo do nutriente no solo (PIMENTEL GOMES, 2009). Todos os parâmetros aparecem de forma não linear em (1.2). Uma vez que pelo menos um dos parâmetros aparece de forma não linear, o modelo é não linear.

A principal vantagem do modelo não linear sobre o linear é que 1) sua escolha está associada ao conhecimento prévio sobre a relação a ser modelada e 2) geralmente apresenta interpretação prática para os parâmetros.

1.1 Motivações

Modelos não lineares (MNL) usualmente são sustentados por alguma informação sobre a relação entre \(Y\) e \(x\). Tal informação está vinculada à diferentes graus de conhecimento como:

1. uma análise de um diagrama de dispersão de \(y\) contra \(x\) que sugere alguma relação funcional;
2. restrições de forma da função (ser monótona, ser sigmóide) conforme necessidade do fenômeno em questão, e.g. o conteúdo acumulado de nutrientes liberado no solo não pode diminuir com o tempo;
3. a solução de uma equação diferencial sustentada por algum príncipio/teoria que serve de premissa para o desenvolvimento do modelo;
4. ou a necessidade de considerar uma equação que tenha interpretação para os parâmetros.

Seja qual for o grau de conhecimento, a escolha de um modelo não linear raramente é empírica.

Um número crescente de pesquisadores compartilham a opinião de que as relações entre variáveis biológicas são melhores descritas por funções não lineares. Processos como crescimento, decaimento, nascimento, mortalidade, abundância, competição e produção raramente são relacionadas linearmente às variáveis explicativas (SCHABENBERGER; PIERCE, 2002 capítulo 5). Nesse sentido, pode se dizer que os MNL melhor descrevem processos mecanísticos e são úteis por acomodarem as restrições referentes à tais processos. Por exemplo, em estudos de produção-adubação sabe-se que os incrementos regulares de adubo (\(x\)) não geram incrementos regulares, mas incrementos decrescentes na produção (\(Y\)). Além disso espera-se que a produção irá estabilizar após certo nível de adubação, pois passa ser limitada por outro fator, mesmo que a adubação seja aumentada indefinidamente. Essa é a lei do mínimo. Mesmo não avaliando a produção sob doses extremas de adubo, pode-se determinar qual seria o seu valor limite ao considerar um MNL apropriado.

De maneira resumida, os MNL têm as seguintes vantagens sobre os modelos lineares (ML):

1. Sua escolha têm sustentação baseada em teoria ou princípios mecanísticos (físicos, químicos ou biológicos) ou qualquer outra informação prévia.
2. Certos parâmetros são quantidade de interesse para o pesquisador e possuem interpretação prática.
3. Podem ser feitas predições fora do domínio observado de \(x\) quando o modelo é apropriado.
4. São parsimoniosos pois tipicamente possuem poucos parâmetros, quase sempre com 4 ou menos parâmetros.
5. Partem do conhecimento do pesquisador sobre o fenômeno alvo.

Em contrapartida, as desvantagens são:

1. Requerem procedimentos iterativos de estimação baseados no fornecimento de valores iniciais para os parâmetros.
2. Métodos de inferência são aproximados o que é uma preocupação em pequenas amostras.
3. Exigem conhecimento do pesquisador sobre o fenômeno alvo.

1.2 Propriedades

Matematicamente, um MNL nada mais é que uma função não linear nos parâmetros. Estatisticamente, um modelo de regressão não linear descreve o comportamento de alguma quantidade relacionada à distribuição de probabilidades de uma variável aleatória \(Y\) por meio de uma função não linear nos parâmetros. Na grande maioria das vezes, a quantidade de interesse é a média de \(Y\). Dessa forma, em nossa notação, a partir de agora aprimorada para haver consistência ao longo texto, \[\begin{equation} \tag{1.3} \text{E}(Y|x) = \eta(x, \boldsymbol{\theta}) \end{equation}\]

representa um modelo que descreve, como quantidade de interesse, a média de uma variável aleatória \(Y\) em termos da variável explicativa \(x\) e do vetor de \(p\) parâmetros \(\boldsymbol{\theta} = (\theta_1, \ldots, \theta_p)^\top\) por meio da função não linear \(\eta\).

Antes de seguir, será feita adequação da notação de (1.1) e (1.2) de acordo com (1.3). Dessa forma \[\begin{equation} \tag{1.4} \begin{aligned} \eta(x, \theta_0, \theta_1, \theta_2) &= \theta_0+\theta_1 x+\theta_2 x^2 \label{eq-qua} \\ \eta(x, \theta_a, \theta_e, \theta_c) &= \theta_a(1-\exp\{-\theta_e(x-\theta_c)\}) \end{aligned} \end{equation}\]

são MNL em que os parâmetros representados por \(\theta\) diferenciam-se pelo índice em subscrito. Em nossa notação, índices numéricos são usados para parâmetros sem, com vaga ou não útil (n.u.), interpretação e letras arábes minúsculas para os interpretáveis. Por exemplo, em (1.4) os índices \(a\), \(e\) e \(c\) correspondem à \(a\)ssíntota, \(e\)ficiência e \(c\)onteúdo para remeter à interpretação.

Normalmente existem restrições ao espaço paramétrico \(\boldsymbol\Theta\) de \(\boldsymbol\theta\) e/ou ao domínio e contra-domínio de \(\eta\) para que a função exista ou tenha interpretação. Por exemplo, em (1.4), os parâmetros \(\theta_a\), \(\theta_e\) e \(\theta_c\) devem ser não negativos bem como \(x\) e \(\eta\) por representarem dose e produção média. Além do mais, os parâmetros possuem unidades de medida (u.m.) que dependem de como aparecem em \(\eta\). O conhecimento da unidade de medida ou dimensionalidade é fundamental para compreensão de seu significado e para uma precisa descrição do modelo.

Por definição, o modelo é não linear se pelo menos uma das derivadas de \(\eta\) com relação a um dos parâmetros em \(\boldsymbol{\theta}\) envolver parâmetros. Ao avaliar-se as derivadas de (1.1), \[\begin{equation} \tag{1.5} \frac{\partial \eta}{\partial \theta_0} = 1, \quad \frac{\partial \eta}{\partial \theta_1} = x, \quad \frac{\partial \eta}{\partial \theta_2} = x^2, \end{equation}\] verifica-se não envolver parâmetros mas apenas as quantidades conhecidas 1, \(x\) e \(x^2\). Por isso (1.1) é um modelo linear nos parâmetros. Por outro lado, ao avaliar-se as derivadas de (1.4) \[\begin{aligned} \frac{\partial \eta}{\partial \theta_a} &= 1-\exp\{-\theta_e(x-\theta_c)\} \\ \frac{\partial \eta}{\partial \theta_e} &= -\theta_a (\theta_c-x) \exp\{-\theta_b(x-\theta_c)\} \\ \frac{\partial \eta}{\partial \theta_c} &= -\theta_a \theta_b\exp\{-\theta_b(x-\theta_c)\}, \end{aligned}\]

observa-se que pelo dois parâmetros foram envolvidos nas derivadas e por isso (1.4) é modelo não linear.

1.2.1 Modelos parcialmente lineares

Alguns autores definem classificações intermediárias. Um modelo é linearizável se por meio de uma transformação se torna um modelo linear. É o caso de \[\begin{equation} \eta(x, \boldsymbol{\theta}) = \exp\{\theta_0+\theta_1 x\} \end{equation}\] que ao aplicar a transformação \(\log\) se transforma em um modelo linear \[\begin{equation} \log(\eta(x, \boldsymbol{\theta})) = \theta_0+\theta_1 x. \end{equation}\]

Modelos em que isso não acontece, como (1.4), são chamados de intrinsicamente não lineares.

Uma classificação útil dos MNL é quanto ao número de parâmetros que ocorrem de forma linear. Nas derivadas de (1.4), aquela com relação a \(\theta_a\) não envolveu \(\theta_a\). Porém, o mesmo não aconteceu para os demais parâmetros. Por esse fato, diz-se que (1.4) é parcialmente linear em \(\theta_a\) pois, se os demais parâmetros fossem conhecidos, teria-se um modelo linear, neste caso do tipo \[\begin{equation} \tag{1.6} \eta(x, \boldsymbol{\theta}) = \theta_a z(x) \end{equation}\]

em que \(z\) é nada mais que uma tranformação (não linear) feita com \(x\). Nesse caso \(z = 1-\exp\{\theta_e(x-\theta_c)\}\), pois considerou-se que \(\theta_e\) e \(\theta_c\) são conhecidos.

Para ser mais preciso, um MNL é linear em um parâmetro quando a segunda derivada com relação a ele for zero. Segundo tal definição tem-se que

\[\begin{aligned} \frac{\partial^2 \eta}{\partial \theta_a^2} &= 0 \\ \frac{\partial^2 \eta}{\partial \theta_e^2} &= -\theta_a(\theta_c-x)^2\exp\{-\theta_e (x-\theta_c)\} \nonumber\\ \frac{\partial^2 \eta}{\partial \theta_c^2} &= -\theta_a \theta_e^2\exp\{-\theta_e (x-\theta_c)\} \nonumber . \end{aligned}\]

Então o modelo (1.4) é parcialmente linear em um parâmetro, \(\theta_a\). Verifica-se que (1.6) é o modelo linear simples pela origem em \(z\).

Por essas definições, pode-se pensar que os ML são um caso particular dos MNL pois são aqueles nos quais as derivadas de primeira ordem não envolvem parâmetros e as derivadas de segunda ordem são zero. Então, os modelos de regressão linear múltipla bem como os modelos polinomiais ou que envolvem transformações das variáveis explicativas, são todos lineares. Tanto que esses modelos podem ser escritos de forma matricial

\[\begin{equation} \tag{1.7} \eta(x, \boldsymbol{\theta}) = \theta_0 + \theta_1 x_1 + \theta_2 x_2+ \ldots + \theta_p x_p = \textbf{X}\boldsymbol{\theta}. \end{equation}\]

1.2.2 Caracterização das funções

Os MNL, embora o nome seja por ter parâmetros de forma não linear, também descrevem relações não lineares entre a variável resposta e a variável preditora. Essas relações apresentam muitas formas e por isso é fundamental a capacidade de descrevê-las para, ou reconhecê-las a partir de, um MNL. A descrição do formato da função é algo obtido via estudo da função que pode considerar a aplicação de 1) limites, 2) derivadas, 3) e integrais, 4) o cálculo de inversas e 5) a avaliação da função em pontos do domínio.

São características de uma função coisas como 1) ter pontos notáveis (ponto crítico, ponto inflexão, ponto de descontinuidade), 2) seu comportamento (tipo de concavidade, tipo de monoticidade) ou a presença de padrões específicos (sigmoide, parabólico). Para referência futura, serão definidas algumas dessas características començando pelos pontos notáveis relacionados ao eixo das coordenadas.

ASS

assíntota superior. Quando \(\lim_{x\to \pm\infty} \eta(x) = c < \infty\), ou seja, tem-se um limite superior \(c\) para \(\eta(x)\) para valores de \(x\) extremos. Produção como função de adubação e curvas de crescimento têm esse padrão. Por exemplo, (1.4) tem ASS com valor limite \(\theta_a\).

ASI

assíntota inferior. Quando \(\lim_{x\to \pm\infty} \eta(x) = c > -\infty\), ou seja, tem-se um limite inferior \(c\) para \(\eta(x)\) para valores de \(x\) extremos. Curvas de retenção de água do solo e modelos liberação de nutrientes têm essa característica. O modelo \(\exp\{-\theta_0 x\}\) tem ASI com valor limite 0.

PO

ponto de origem ou intercepto. Valor de \(\eta(0)\). É um ponto característico de muitos modelos e por isso é representado por um parâmetro. No modelo \(\theta_o + \frac{\theta_a x}{\theta_v + x}\) tem-se que \(\theta_o\) é o PO e, para estudos de produção-adubação, é a produção esperada sem adubo. A ASS é \(\theta_a\).

PON

ponto de origem nulo. Quando \(\eta(0) = 0\). O modelo \(\theta_0(1 - \exp\{-\theta_1 x\}\) tem PON ao passo que (1.4) tem PO dependente dos parâmetros.

Como esses pontos se referem ao eixo das coordenadas, todos carregam a unidade de medida de \(\eta(x)\) que é \(\text{Y}\). Pontos característicos no eixo das abcissas carregam a unidade de \(x\) que é \(\text{X}\). São descritos a seguir os pontos que se destacam no eixo das abcissas.

PC

ponto crítico. Quando para algum \(x\) tem-se \(\eta'(x) = 0\). Se \(\eta''(x) > 0\) o ponto é de mínimo e se \(\eta''(x) < 0\) é de máximo. O PC é um ponto característico de interesse em estudos de otimização como os de produção-adubação e curvas de produção-densidade. O modelo (1.1) tem PC em \(x = \frac{-\theta_1}{2\theta_2}\).

PI

ponto de inflexão. Quando para algum \(x\) tem-se \(\eta''(x) = 0\). É um ponto característico das curvas sigmoides consideradas em estudos de crescimento/progresso. Representa o valor em \(x\) que corresponde à maior taxa, ou seja, a fase de crescimento/progresso mais acelerado, a idade de mais alta conversão alimentar. O modelo \(1/(1+\exp\{-\theta_s(x-\theta_i)\})\) tem PI representado por \(\theta_i\).

PS

ponto de simetria. Quando para algum \(x\) tem-se \(|\eta(x+\delta)-\eta(x)| = |\eta(x-\delta)-\eta(x)|\) para todo \(\delta>0\). Em outras palavras, PS corresponde a um valor \(x\) que traça um eixo vertical de simetria. Isso acontece, por exemplo, no modelo quadrático (1.1) que tem PS em \(x = \frac{-\theta_1}{2\theta_2}\) e no modelo logístico, que apresenta simetria na primeira derivada.

PD

ponto de descontinuidade. Quando para algum \(x\), \(\delta>0\) e alguma derivada de \(\eta\) em relação a \(x\) de ordem \(k = 0, 1, \ldots,\) tem-se \(\lim_{\delta \to 0}\eta^{(k)}(x + \delta) \neq \lim_{\delta\to 0}\eta^{(k)}(x - \delta)\). É um ponto característico de modelos segmentados, como o linear-plato, quadrático-plato, bi-linear. No modelo linear-plato, o PD representa o valor em \(x\) para a troca de regimes, ou seja, para valores menores que \(\delta\), a resposta tem taxa diferente de zero e para valores acima, a função é constante. Por isso tal modelo é considerado em estudos de produção-adubação e número ótimo de parcelas.

PF

ponto de fração. Suponha que \(\eta(x)\) seja uma função monótona de contra-domínio limitado, ou seja, \(a \leq \eta(x) \leq b\), para \(a<b\), então o valor \(x\) para o qual \(\eta(x) = a+q(b-a)\) é um ponto de fração \(q\), \(0<q<1\). Funções sigmoides são limitadas pois têm assíntotas e um ponto de fração meio, por exemplo, é valor \(x\) correspondente ao ponto médio entre os limites da função. Em estudos de liberação de nutrientes no solo, o PF é importante para saber o tempo necessário para liberação de \(q=90\)% do total e em estudos de mortalidade-resposta é considerado para estabelecer a dose letal para \(q = 50\)% da população (\(DL_{50\%}\)). No modelo \(\frac{\theta_a x}{\theta_v+x}\), o PF meio (\(q=0,5\)) é representado por \(\theta_v\), uma vez que o contra-domínio é [0,\(\theta_a\)).

PZ

ponto de zero ou raíz da função. São os valores de \(x\) para os quais \(\eta(x) = 0\). Em alguns modelos, tais pontos característicos são representados por parâmetros como é o caso do modelo beta generalizado, \(\theta_0(x-\theta_1)^{\theta_2}(\theta_3-x)^{\theta_4}\), considerado em estudos de crescimento-temperatura de fungos para o qual \(\theta_1\) e \(\theta_3\) são os PZ da função.

POH

ponto de offset horizontal. Análogo ao PO só que para o eixo \(x\), é também um PZ. Em certos contextos, como liberação de nutrientes descrito por \(\theta_a(1-\exp\{-\theta_c(x-\theta_h)\})\) sendo o POH o parâmetro \(\theta_h\), é interpretado como período de aquecimento, uma vez que a liberação ocorre para \(x>\theta_h\), para \(x<\theta_h\) não ocorre liberação pois os microorganismos envolvidos no processo estavam se “aquecendo”, ou melhor, estavam crescendo às custas dos nutrientes não liberados mas por eles consumidos nesse período.

Além dos pontos característicos, aspectos da forma de uma função são úteis para classificá-la ou selecioná-la. Dentre eles, alguns são destacados a seguir.

MC

monótona crescente. Quando \(\eta(x_1) < \eta(x_2)\) para todo \(x_1 < x_2\) o que implica em \(\eta'(x) > 0\), ou seja, a função é crescente. O modelo (1.4) é MC.

MND

monótona não decrescente. Quando \(\eta(x_1) \leq \eta(x_2)\) para todo \(x_1 < x_2\) o que implica em \(\eta'(x) \geq 0\), ou seja, a função é crescente ou constante.

MD

monótona decrescente. Quando \(\eta(x_1) > \eta(x_2)\) para todo \(x_1 < x_2\) o que implica em \(\eta'(x) < 0\), ou seja, a função é decrescente.

MNC

monótona decrescente. Quando \(\eta(x_1) \geq \eta(x_2)\) para todo \(x_1 < x_2\) o que implica em \(\eta'(x) \leq 0\), ou seja, a função é decrescente ou constante.

CCV

côncava. Quando \((\eta(x) + \eta(x + \delta))/2 < \eta(x + \delta/2)\) para todo \(x\) e \(\delta > 0\). Em outras palavras, todo segmento de reta unindo dois pontos sobre a curva, (\(x_1\), \(\eta(x_1)\)) e (\(x_1\), \(\eta(x_1)\)), está abaixo da curva no intervalo definido pelas projeções destes pontos na abcissa (\(x_1\) e \(x_2\)). Tem-se que (1.4) é CCV.

CVX

convexa. Quando \((\eta(x) + \eta(x + \delta))/2 > \eta(x + \delta/2)\) para todo \(x\) e \(\delta > 0\). Em outras palavras, todo segmento de reta unindo dois pontos sobre a curva, (\(x_1\), \(\eta(x_1)\)) e (\(x_1\), \(\eta(x_1)\)), está acima da curva no intervalo definido pelas projeções destes pontos na abcissa (\(x_1\) e \(x_2\)). Tem-se que \(\exp\{-\theta_0 x\}\) é CVX.

SEG

segmentado. Todo modelo segmentado tem PD com execessão apenas em \(\eta(x)\). São assim os modelos linear-platô, quadrático-platô, bi-linear, tri-linear, etc.

AAC

área abaixo da curva. Quando \(|\int_{\forall x} \eta(x)\, \text{d}x| < \infty\), em outras palavras, a integral de \(\eta(x)\) em todo domínio de \(x\) tem valor finito. É um caso, por exemplo, dos modelos baseados nas funções de densidade de probabilidade, como o modelo gama para curvas de lactação e o modelo beta para crescimento-temperatura em microbiologia e fitopatologia. Frequentemente se tem AAC tem também PC e ASS e ASI são 0. O modelo gama de lactação \(\theta_0 x^{\theta_1} \exp\{-\theta_2 x\}\) é AAC e o PC é de máximo em \(x=\theta_1/\theta_2\).

Certas combinações entre pontos e aspectos característicos resultam em padrões específicos de comportamento de função. Por vezes é mais rápido reconhecer as propriedades de uma função pela sua aparência com algum padrão específico. Alguns dos mais comuns são apresentados a seguir.

SIG

sigmóide. A curva tem formato de S ou S invertido. Toda sigmóide é MC ou MD, tem PI, tem ASS e ASI e eventualmente pode ter PS, além de permitir definir PF\(_q\).

SIN

sinodal. Tem formato de sino. Com isso, toda sinodal tem PC, eventualmente pode ter PS, ASS, ASI e AAC.

PAR

parabólica. Tem formato de parabola ou de U, U invertido. Sendo assim, toda parabólica tem PC, é CON ou CVX e eventualmente pode ter PS.

SEN

senóide. Tem formato de onda, é oscilatória ou periódica. São funções consideradas para modelar processos cíclicos como níveis hormonais em função dos períodos reprodutivos, por exemplo.

EXP

exponencial ou assintótica. Tem formato de J, valendo quatro orientações resultantes ao coexistir as características monótona crescente/decrescente com concava/convexa. Em termos de aplicação, tem-se que as MC-CON são consideradas para descrever a produção-adubação, as MC-CVX o crescimento populacional explosivo, as MD-CON a produção-desfolha e MC-CVX o decaimento na liberação diária de um nutriente pelo solo.

Todas essas propriedades são facilmente verificadas por meio de gráficos da função. Para melhor compreender o significado de cada item descrito, a coleção funções na Figura 1.1 destaca os pontos característicos e aspectos de forma de curvas variadas. As funções em A e B são monótonas, crescente e decrescente, têm ambas assíntotas e pontos característicos como PO, PI e PF mas somente A é simétrica com relação ao PI. Nas funções C e D destaca-se que são assintóticas, de acúmulo e decaimento, são concava e convexa, têm POH e PZ e são segmentadas. Em E e F têm-se funções com PC, no entanto E tem AAC, não tem PS, tem PON.

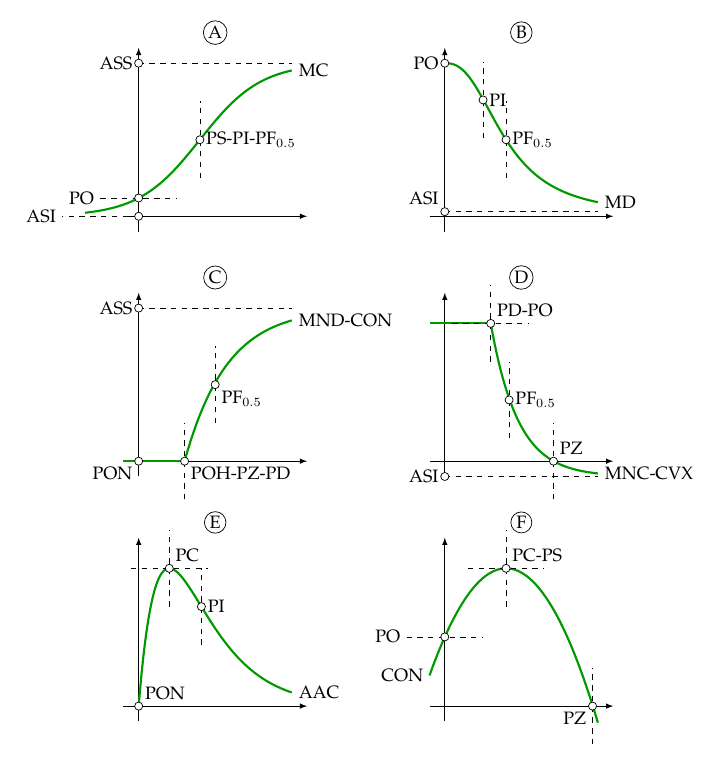
Figura 1.1: Funções não lineares com destaque para os pontos característicos e formas.

Referências Bibliográficas

PIMENTEL GOMES, F. Curso de estatística experimental. 15th ed. Piracicaba: FEALQ, 2009.

SCHABENBERGER, O.; PIERCE, F. J. Contemporary Statistical Models for the Plant and Soil Sciences. Boca Raton: CRC Press, 2002.