Seguinte: Interpretação do coeficiente de Acima: Correlação Anterior: Relações entre variáveis
Seja
![]() o conjunto das medidas de uma das variáveis
(alturas dos pais), e seja
o conjunto das medidas de uma das variáveis
(alturas dos pais), e seja
![]() as medidas da outra
variável (alturas dos filhos). Seja
as medidas da outra
variável (alturas dos filhos). Seja ![]() ,
,
![]() ,
, ![]() e
e ![]() as médias e desvios padrão amostrais dos dois
conjuntos de dados.
as médias e desvios padrão amostrais dos dois
conjuntos de dados.
Primeiro calcule para cada indivíduo:
Se valores altos de ![]() acompanham valores baixos de
acompanham valores baixos de ![]() e vice-versa
então a maioria dos valores
e vice-versa
então a maioria dos valores ![]() serão negativos.
serão negativos.
Se não existir associação entre ![]() e
e ![]() então se tomarmos a média aritmética dos
valores
então se tomarmos a média aritmética dos
valores ![]() , valores positivos e negativos tenderão a se cancelar.
, valores positivos e negativos tenderão a se cancelar.
Para obter uma medida do grau de associação da relação linear entre duas variáveis, usamos o coeficiente de correlação de Pearson, definido como:
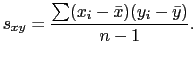
Para os dados do exemplo acima, temos ![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() a
partir dos quais podemos calcular que
a
partir dos quais podemos calcular que ![]() .
.
Assim como para médias e desvios padrão, existe uma letra Grega
especial que utlizamos para o coeficiante de correlação
populacional: ![]() . Podemos considerar
. Podemos considerar ![]() como sendo uma
estimativa de
como sendo uma
estimativa de ![]() , exatamente como
, exatamente como ![]() é uma estimativa da
média populacional
é uma estimativa da
média populacional ![]() .
.
Abaixo estão exemplos de dados com seus coeficientes de correlação correspondentes.
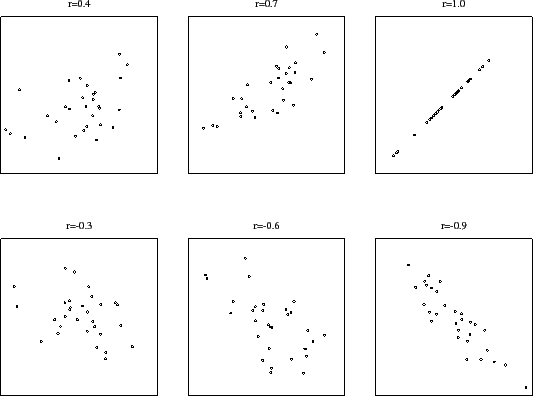
Silvia Shimakura 2011-04-04