Seguinte: Exemplo: Níveis plasmáticos de Acima: Conceitos fundamentais Anterior: Estimadores
Diferentes amostras podem ser retiradas de uma mesma população, e amostras diferentes podem resultar em estimativas diferentes. Isto é, um estimador é uma variável aleatória, podendo assumir valores diferentes para cada amostra.
Então, ao invés de estimar o parâmetro de interesse por um único valor, é muito mais informativo estimá-lo por um intervalo de valores que considere a variação presente na amostra e que contenha o seu verdadeiro valor com determinada confiança.
Este intervalo é chamado de intervalo de confiança.
Para construir um intervalo de confiança precisamos conhecer a distribuição de probabilidade do estimador. Lembre que um estimador é uma variável aleatória e que uma variável aleatória é completamente caracterizada por sua distribuição de probabilidade.
Por exemplo, o intervalo de confiança para ![]() , é obtido usando o seguinte
resultado da Teoria Estatística:
, é obtido usando o seguinte
resultado da Teoria Estatística:
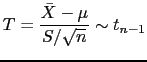
Então, mesmo não se conhecendo ![]() , podemos calcular probabilidades
envolvendo a estatística
, podemos calcular probabilidades
envolvendo a estatística ![]() .
.
Isso nos permite construir o intervalo de confiança para ![]() da seguinte forma:
da seguinte forma:
Através da tabela da distribuição ![]() obtemos um valor
obtemos um valor ![]() tal que
tal que
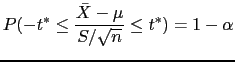
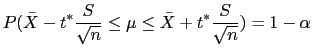
![$\displaystyle \left[\bar{X}-t^* \frac{S}{\sqrt{n}} ; \bar{X}+t^* \frac{S}{\sqrt{n}}\right]$](img299.png)
Portanto, o intervalo de confiança para ![]() é centrado na estimativa do
efeito, e varia de uma quantidade
é centrado na estimativa do
efeito, e varia de uma quantidade ![]() desvios-padrão para baixo até o mesmo
número de desvios-padrão para cima.
desvios-padrão para baixo até o mesmo
número de desvios-padrão para cima.
shimakur 2016-02-18