A distribuição Normal

A distribuição Normal é a mais familiar das distribuições de probabilidade e também uma das mais importantes em estatística.

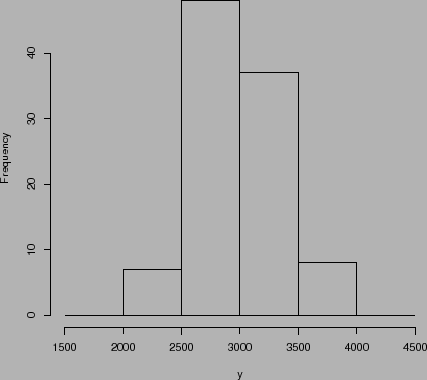
Exemplo: O peso de recém-nascidos é uma variável aleatória contínua. A Figura 32 e Figura 33 abaixo mostram a distribuição de frequências relativas de 100 e 5000 pesos de recém-nascidos com intervalos de classe de 500g e 125g, respectivamente.

Figura 32: Histograma de frequências relativas a 100 pesos de reçém-nascidos com intervalo de classe de 500g

Figura 33: Histograma de frequências relativas a 5000 pesos de reçém-nascidos com intervalo de classe de 125g

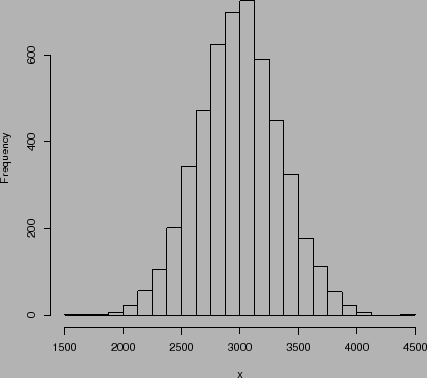O segundo histograma é um refinamento do primeiro, obtido aumentando-se o tamanho da amostra e reduzindo-se a amplitude dos intervalos de classe. Ele sugere a curva na Figura 34, que é conhecida como curva normal ou Gaussiana.

Figura 34: Função de densidade de probabilidade para a variável aleatória contínua X=peso do recém-nascido (g)

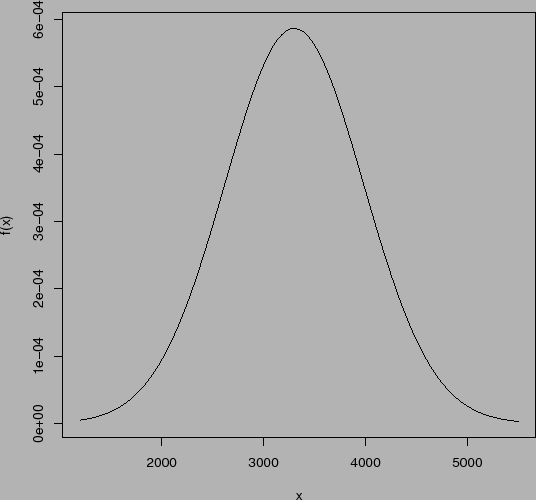A variável aleatória considerada neste exemplo e muitas outras variáveis da área biológica podem ser descritas pelo modelo normal ou Gaussiano.

A equação da curva Normal é especificada usando 2 parâmetros: a média $\mu$, e o desvio padrão $\sigma$.

Figura 35: distribuições normais com mesma média $\mu$ e vários valores de $\sigma$

Denotamos N( $\mu, \sigma$) à curva Normal com média $\mu$ e desvio padrão $\sigma$.

A média refere-se ao centro da distribuição e o desvio padrão ao espalhamento (ou achatamento) da curva.

A distribuição normal é simétrica em torno da média o que implica que a média, a mediana e a moda são todas coincidentes.

Para referência, a equação da curva é

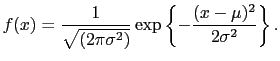$$f(x) = \frac{1}{\sqrt{(2\pi\sigma^2)}}\exp\left\{-\frac{(x-\mu)^2} {2\sigma^2}\right\}.$$ (7)

Felizmente, você não tem que memorizar esta equação. O importante é que você entenda como a curva é afetada pelos valores numéricos de $\mu$ e $\sigma$. Isto é mostrado no diagrama da Figura 35.

A área sob a curva normal (na verdade abaixo de qualquer função de densidade de probabilidade) é 1. Então, para quaisquer dois valores específicos podemos determinar a proporção de área sob a curva entre esses dois valores.

Para a distribuição Normal, a proporção de valores caindo dentro de um, dois, ou três desvios padrão da média são:

Range	Proportion
$\mu \pm 1\sigma$	68.3%
$\mu \pm 2\sigma$	95.5%
$\mu \pm 3\sigma$	99.7%

Exemplo: Suponhamos que no exemplo do peso do recém-nascidos $\mu=2800g$ e $\sigma=500g$. Então:

$P(2300 \leq X \leq 3300)=0,683$
$P(1800 \leq X \leq 3800)=0,955$
$P(1300 \leq X \leq 4300)=0,997$

Usando este modelo podemos dizer que cerca de 68% dos recém-nascidos pesam entre 2300g e 3300g. O peso de aproximadamente 95% dos recém-nascidos está entre 1800g e 3800g. Praticamente todos os bebês desta população nascem com peso no intervalo (1300,4300).

Na prática desejamos calcular probabilidades para diferentes valores de $\mu$ e $\sigma$.

Para isso, a variável $X$ cuja distribuição é $N(\mu,\sigma)$ é transformada numa forma padronizada $Z$ com distribuição $N(0,1)$ (distribuição normal padrão) pois tal distribuição é tabelada.

A quantidade $Z$ é dada por

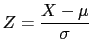$$Z=\frac{X-\mu}{\sigma}$$ (8)

Exemplo: Suponha que a pressão arterial sistólica em pessoas jovens saudáveis tenha distribuição $N(120,10)$.

1. Qual é a probabilidade de se encontrar uma pessoa com pressão sistólica acima de $140 mmHg$?
   

   $$\begin{array}{lll} P(X \geq 140)&=&P(\frac{X-120}{10}\geq \fr... ...)=\\ &=&1-P(Z<2)=\\ &=&1-0,9772=\\ &=&0,0228 \end{array}$$

   
   Ou seja, 2,28% das pessoas jovens e sadias têm pressão sistólica acima de 140 $mmHg$.

2. Quais são os limites de um intervalo simétrico em relação à média que engloba 95% dos valores das pressões sistólicas de pessoas jovens e sadias?

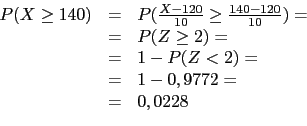   Neste caso queremos encontrar $a$ e $b$ tais que: $P(a \leq X \leq b)=0,95$.

   Primeiro padronizamos essa probabilidade, isto é,

   $$P(a \leq X \leq b)=P\left( \frac{a-120}{10} \leq \frac{X-120}{10} \leq \frac{b-120}{10}\right)=0,95$$

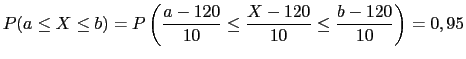
   Ou seja, $P(a^\prime \leq Z \leq b^\prime)=0,95$. Escolhendo uma solução simétrica temos $-a^\prime=b^\prime$.

   Como $P(Z \leq b^\prime)=0.975$, da tabela da gaussiana padrão obtemos $a^\prime=-1,96$ e $b^\prime=1,96$.

   Consequentemente, $\frac{a-120}{10}=-1,96$ e $\frac{b-120}{10}=1,96$, ou seja, $a=100,4$ e $b=139,6$.

   Para essa população de jovens saudáveis, o intervalo $[100,4; 139,6]$ engloba 95% dos valores pressóricos, isto é, aproximadamente entre 100 $mmHg$ e 140 $mmHg$.