Definição frequentista

Na maioria das situações práticas, os eventos simples do espaço amostral não são equiprováveis e não podemos calcular probabilidades usando a definição clássica. Neste caso, vamos calcular probilidades como a frequência relativa de um evento. Segue um exemplo que ilustra o método.

Exemplo 1: Uma amostra de 6800 pessoas de uma determinada população foi classificada quanto à cor dos olhos e à cor dos cabelos. Os resultados foram:

Tabela 11: Classificação de uma amostra de 6800 pessoas quanto à cor dos olhos e à cor dos cabelos

	Cor dos cabelos
Cor dos olhos	Loiro	Castanho	Preto	Ruivo	Total
Azul	1768	807	189	47	2811
Verde	946	1387	746	53	3132
Castanho	115	438	288	16	857
Total	2829	2632	1223	116	6800

Considere o experimento aleatório que consiste em classificar um indivíduo quanto à cor dos olhos. O espaço amostral é $E=\{A,V,C\}$, em que:

A={a pessoa tem olhos azuis}
V={a pessoa tem olhos verdes}
C={a pessoa tem olhos castanhos}

Os eventos acima não são equiprováveis. Então vamos calcular a probabilidade de ocorrer um evento como a frequência relativa deste evento:

$$P(A) = \frac{\mbox{número de pessoas de olhos azuis}}{\mbox{número de pessoas na amostra}}=\frac{2811}{6800}=0,4134$$ (2)

O valor obtido é na verdade uma estimativa da probabilidade. A qualidade desta estimativa depende do número de replicações do experimento, ou seja, do tamanho da amostra.

À medida que o tamanho da amostra cresce, a estimativa aproxima-se mais do valor verdadeiro da probabilidade. Vamos, no entanto, assumir que o número de replicações é suficientemente grande para que a diferença entre a estimativa e o valor verdadeiro da probabilidade seja desprezível.

As probabilidades dos eventos V e C são:

$P(V)=\frac{3132}{6800}=0,4606$ e $P(C)=\frac{857}{6800}=0,1260$

Observe que $P(A)+P(V)+P(C)=1$. Este resultado é geral, uma vez que a união destes eventos corresponde ao espaço amostral.

Seja $\bar{A}$ o evento {a pessoa não tem olhos azuis}. O evento $\bar{A}$ é chamado de evento complementar de $A$ e $P(\bar{A})=\frac{3132+857}{6800}=0,5866=1-P(A)$.

Estes resultados são propriedades de probabilidades. Seja $A$ um evento qualquer no espaço amostral $E$. Então valem as propriedades:

1. $0\leq P(A) \leq 1$
2. $P(E)=1$
3. $P(\bar{A})=1-P(A)$

Voltando ao exemplo, vamos calcular algumas probabilidades. Seja $L$ o evento {a pessoa tem cabelos loiros}.

Qual a probabilidade de uma pessoa ter olhos azuis e cabelos loiros?

O evento {a pessoa tem olhos azuis e cabelos loiros} é chamado de evento interseção. Ele contém todos os elementos do espaço amostral pertencentes concomitantemente ao evento $A$ e ao evento $L$ e será denotado por $A \cap L$, e a probabilidade deste evento é:

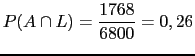$$P(A \cap L) = \frac{1768}{6800}=0,26$$ (3)

Qual a probabilidade de uma pessoa ter olhos azuis ou cabelos louros?

O evento {a pessoa tem olhos azuis ou cabelos louros} é chamado de evento união e será denotado por $A \cup L$. Ele contém todos os elementos do espaço amostral que estão em $A$, ou somente em $L$, ou em ambos, e a probabilidade deste evento é:

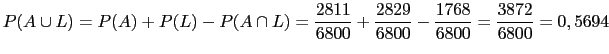$$P(A \cup L) = P(A)+P(L)-P(A\cap L)= \frac{2811}{6800}+\frac{2829}{6800}-\frac{1768}{6800}=\frac{3872}{6800}=0,5694$$ (4)

Para quaisquer dois eventos A e B do espaço amostral, podemos calcular a probabilidade do evento união da seuignte forma: $P(A\cup B)=P(A)+P(B)-P(A\cap B)$

Se os eventos são mutuamente exclusivos, isto é, eles não podem ocorrer simultaneamente, $P(A\cap B)=0$ e consequentemente

$$P(A\cup B)=P(A)+P(B)$$

Num exemplo de lançamento de um dado como os eventos $P=\{$sair número par$\}$ e $I=\{$sair número ímpar$\}$ são mutuamente exclusivos, $P(P\cup I)=P(P)+P(I)=3/6+3/6=1$.

Entretanto, os eventos $O=\{$sair número 1 ou 3$\}$ e $Q=\{$sair número maior que 2$\}$ não são mutuamente exclusivos, pois $O\cap Q=\{3\}$.

Neste caso, $P(O\cup Q)=P(O)+P(Q)-P(O\cap Q)=2/6+4/6-1/6=5/6$.