Seguinte: Exemplos Acima: Testes de Hipóteses Anterior: Decisões e poder
Vimos no Capítulo 5 e nas seções anteriores deste capítulo como
construir intervalos e testes de hipóteses para os principais
parâmetros populacionais. Em todos os, supusemos dado o nível de
confiança desses intervalos e testes. Evidentemente, o nível de
confiança deve ser fixado de acordo com a probabilidade de acerto que
se deseja ter na estimação por intervalo e testes. Sendo conveniente,
o nível de confiança pode ser aumentado até tão próximo de 100%
quanto se queira, mas isso resultará em intervalos de amplitude cada
vez maiores (e testes com poderes cada vez menores), o que significa
perda de precisão na estimação.
É claro que seria desejável termos intervalos com alto nível de
confiança e pequena probabilidade de erro e grande precisão. Isso
porém requer uma amostra suficientemente grande, pois, para ![]() fixo,
confiança e precisão variam em sentidos opostos.
fixo,
confiança e precisão variam em sentidos opostos.
Veremos a seguir como determinar o tamanho das amostras necessárias
nos casos de estimação da média ou de uma proporção populacional.
Vimos na Seção 5.4 que o intervalo de confiança de 95% para a média
![]() da população quando
da população quando ![]() é conhecido tem semi-amplitude
é conhecido tem semi-amplitude ![]() dada pela expressão
dada pela expressão
Não conhecendo o desvio-padrão da população, deveríamos subtituí-lo
por sua estimativa ![]() e usar
e usar ![]() de Student na expressão
acima. Ocorre porém que não tendo ainda sido retirada a amostra, não
dispomos em geral do valor de
de Student na expressão
acima. Ocorre porém que não tendo ainda sido retirada a amostra, não
dispomos em geral do valor de ![]() . Se não conhecemos nem ao menos um
limite superior para
. Se não conhecemos nem ao menos um
limite superior para ![]() , a única solução será colher uma
amostra-piloto de
, a única solução será colher uma
amostra-piloto de ![]() elementos para, com base nela obtermos uma
estimativa de
elementos para, com base nela obtermos uma
estimativa de ![]() , empregando a seguir a expressão
, empregando a seguir a expressão
Procedemos de forma análoga se desejamos estimar uma proporção
populacional com determinada confiança e dada precisão. No caso de
população suposta infinita, da expressão
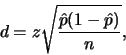
![\includegraphics[width=2.8in]{pics/parab.ps}](img185.png)
Se substituirmos, ![]() por seu valor máximo, 1/4, seguramente o
tamanho de amostra obtido será suficiente para a estimação de qualquer
que seja
por seu valor máximo, 1/4, seguramente o
tamanho de amostra obtido será suficiente para a estimação de qualquer
que seja ![]() . Isso equivale a considerar
. Isso equivale a considerar