Seguinte: A distribuição Poisson Acima: Distribuições teóricas de frequências Anterior: A distribuição Normal
Suponha que ![]() experimentos independentes, ou ensaios, são
executados, onde
experimentos independentes, ou ensaios, são
executados, onde ![]() é um número fixo, e que cada experimento resulta
num ``sucesso'' com probabilidade
é um número fixo, e que cada experimento resulta
num ``sucesso'' com probabilidade ![]() e numa ``falha'' com
probabilidade
e numa ``falha'' com
probabilidade ![]() . O número total de sucessos,
. O número total de sucessos, ![]() , é uma variável
aleatória com parâmetros
, é uma variável
aleatória com parâmetros ![]() e
e ![]() .
.
Por exemplo, uma moeda é lançada 10 vezes e o número total de caras é contado (aqui ``cara'' é um sucesso).
A probabilidade que ![]() , denotada por
, denotada por ![]() , pode ser encontrada como:
, pode ser encontrada como:
| (4) |
A média de um variável aleatória Binomial é ![]() e a variância é
e a variância é ![]() .
.
Considere o seguinte exemplo. Suponha que num pedigree humano
envolvendo albinismo (o qual é recessivo), nós encontremos um
casamento no qual sabe-se que ambos os parceiros são heterozigotos
para o gene albino. De acordo com a teoria Mendeliana, a probabilidade
de que um filho desse casal seja albino é um quarto. (Então a
probabilidade de não ser albino é ![]() .)
.)
Agora considere o mesmo casal com 2 crianças. A chance de que ambas
sejam albinas é
![]() .
A desma forma, a chance de ambas serem normais é
.
A desma forma, a chance de ambas serem normais é
![]() . Portanto, a probabilidade
de que somente uma seja um albina deve ser
. Portanto, a probabilidade
de que somente uma seja um albina deve ser
![]() .
Alternativamente, poderiamos ter usado a formula
acima com
.
Alternativamente, poderiamos ter usado a formula
acima com ![]() ,
, ![]() , and
, and ![]() .
.
Se agora considerarmos a família com ![]() crianças, as probabilidades
de existam
crianças, as probabilidades
de existam
![]() crianças albinas, onde a probabilidade de albinismo
é
crianças albinas, onde a probabilidade de albinismo
é ![]() , são dadas por
, são dadas por
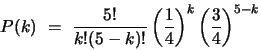 |
(5) |
![\includegraphics[width=3.1in]{pics/binbar.ps}](img87.png)
Silvia E Shimakura 2006-08-30