Seguinte: A distribuição Binomial Acima: Distribuições teóricas de frequências Anterior: Distribuições teóricas de frequências
A distribuição Normal é a mais familiar das distribuições de probabilidade e também uma das mais importantes em estatística. Esta distribuição tem uma forma de sino.
![\includegraphics[width=5in]{pics/normal.ps}](img55.png)
A equação da curva Normal é especificada usando 2 parâmetros: a média populacional ![]() , e o desvio padrão populacional
, e o desvio padrão populacional
![]() , ou equivalentemente a variância populacional
, ou equivalentemente a variância populacional
![]() . Denotamos N(
. Denotamos N(![]() ) à curva Normal com média
) à curva Normal com média
![]() e variância
e variância ![]() . A média refere-se ao centro da
distribuição e o desvio padrão ao espalhamento de curva. A
distribuição normal é simétrica em torno da média o que implica que e
média, a mediana e a moda são todas coincidentes.
Para referência, a equação da curva é
. A média refere-se ao centro da
distribuição e o desvio padrão ao espalhamento de curva. A
distribuição normal é simétrica em torno da média o que implica que e
média, a mediana e a moda são todas coincidentes.
Para referência, a equação da curva é
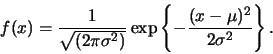 |
(1) |
Felizmente, você não tem que memorizar esta equação. O importante é
que você entenda como a curva é afetada pelos valores numéricos de
![]() e
e ![]() . isto é mostrado no diagrama abaixo.
. isto é mostrado no diagrama abaixo.
![\includegraphics[width=4in]{pics/normstu.ps}](img59.png)
A área sob a curva normal (na verdade abaixo de qualquer função de densidade de probabilidade) é 1. Então, para quaisquer dois valores específicos podemos determinar a proporção de área sob a curva entre esses dois valores. Para a distribuição Normal, a proporção de valores caindo dentro de um, dois, ou três desvios padrão da média são:
| Range | Proportion |
|
|
68.3% |
|
|
95.5% |
|
|
99.7% |
Este resultado é usado da seguinte maneira. Suponha que os comprimentos de um particular tipo de peixe podem ser descritos por uma distribuição normal, com média 140mm e desvio padrão 15mm. Podemos calcular a proporção dos peixes que têm comprimentos entre 110 e 170mm, por exemplo, como a proporção da área sob a curva entre 110 e 170mm.
Então em nosso exemplo, cerca de 95% dos peixes tem comprimentos entre 110mm e 170mm.
Na prática desejamos calcular probabilidades para diferentes valores
de ![]() e
e ![]() . Para isso, a variável
. Para isso, a variável ![]() cuja distribuição é
cuja distribuição é
![]() é transformada numa forma padronizada
é transformada numa forma padronizada ![]() com
distribuição
com
distribuição ![]() (distribuição normal padrão) pois
tal distribuição é tabelada. A quantidade
(distribuição normal padrão) pois
tal distribuição é tabelada. A quantidade ![]() é dada por
é dada por
| (2) |
Exemplo: A concentração de um poluente em água liberada por uma fábrica tem distribuição N(8,1.5). Qual a chance, de que num dado dia, a concentração do poluente exceda o limite regulatório de 10 ppm?
A solução do problema resume-se em determinar a proporção da
distribuição que está acima de 10 ppm, ie ![]() .
Usando a estatística z temos:
.
Usando a estatística z temos:
| (3) |
Exercício: A concentração de cadmio em cinzas de um certo lixo radioativo tem distribuição N(1,0.72). Quais são as chances de que uma amostra aleatória das cinzas tenha uma concentração de cadmio entre 0.5 e 1.75 ppm?
Silvia E Shimakura 2006-08-30