Amostras pareadas

Num estudo pareado, temos duas amostras mas cada observação da primeira amostra é pareada com uma observação da segunda amostra.

Tal delineamento ocorre, por exemplo, num estudo de medidas feitas antes e depois no mesmo indivíduo ou num estudo de gêmeos (em que cada conjunto de gêmeos forma um dado pareado).

Como esperado, as duas observações do mesmo indivíduo (ou de um conjunto de gêmeos) são mais prováveis de serem similares, e portanto não são considerados estatísticamente independentes.

Com dados pareados, podemos usar a seguinte notação:

$$\begin{eqnarray*} x_{1i} &=& \mbox{medida 1 do par $i$},\\ x_{2i} &=& \mbox{medida 2 do par $i$} \end{eqnarray*}$$

a então escrevemos as diferenças nas medidas de cada par como

$$d_{i} = x_{2i} - x_{1i}.$$

Agora temos uma amostra de diferenças $d_i$, e podemos usar os métodos para uma única amostra que já estamos familiares.

Podemos calcular um intervalo de confiança para a diferença média e testar se a diferença média é igual a zero ou não.

Nos referimos a tal teste como um t-test pareado ao contrário do test-t para duas amostras independentes que veremos a seguir.

Note que neste caso estamos interessados na diferença média enquanto que quando temos duas amostras independentes, estaremos interessados na diferença das médias.

Ainda que numericamente estas quantidades sejam as mesmas, conceitualmente elas são diferentes.

Exemplo: A mudança nos valores de imc de indivíduos do início ao final de seis meses tratamento foram:

$$\begin{array}{rrrrrr} -1.5 & -0.6 & -0.3 & 0.2 & -2.0 & -1.2 \end{array}$$

A média e o desvio padrão são $-0.9$ e $0.81$, respectivamente. Então o erro padrão é $0.81/\sqrt{6} = 0.33$.

Podemos agora realizar um test-$t$ pareado para testar a hipótese nula de que a perda média de imc é 0. Para isso calculamos

$$t = \frac{\bar{d}-0}{\mbox{SE}(\bar{d})} = \frac{-0.9}{0.33} = -2.73.$$

Note que este valor é negativo (porque a mudança média observada foi a redução no imc -- um valor positivo seria um aumento no imc).

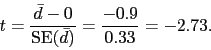
Observamos o valor absoluto da estatística de teste (2.73) na tabela, usando a linha com $n-1=5$ graus de liberdade.

A quinta linha da tabela mostra que $0.01<p<0.05$ (porque o valor 2.73 está entre os valores tabelados 2.571 e 4.032). Então, rejeitamos a hipótese nula ao nível de 5%.

Podemos concluir que existem evidências ao nível de 5% de que há uma redução média de imc durante o período de seis meses em indivíduos sujeitos ao tratamento.

Podemos adicionar à nossa conclusão o intervalo de confiança de 95% para a redução média no imc:

$$-0.9 \pm 2.57 \times 0.33 = -0.9 \pm 0.85 = (-1.75,-0.05)$$

Estamos 95% confiantes que a redução média de imc está entre 0.05 e 1.75.

Suposições feitas: a distribuição das mudanças de imc não é muito diferente de uma Normal.