Agora suponha que tenhamos um valor hipotético 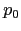 para uma
proporção. Podemos realisar um teste de H
para uma
proporção. Podemos realisar um teste de H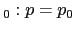 praticamente da mesma forma que o test-t acima. A
dualidade com intervalos de confiança segue exatamente da mesma
forma.
praticamente da mesma forma que o test-t acima. A
dualidade com intervalos de confiança segue exatamente da mesma
forma.
Suponha que tenhamos uma amostra aleatória de tamanho 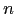 de uma
população de interesse onde a verdadeira proporção de membros numa
categoria em particular é
de uma
população de interesse onde a verdadeira proporção de membros numa
categoria em particular é 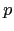 . A hipótese nula é H
. A hipótese nula é H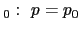 .
Se o número observado na categoria de interesse é
.
Se o número observado na categoria de interesse é 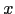 , então um teste
da hipótese é como segue:
, então um teste
da hipótese é como segue:
- Estabeleça a hipótese nula, H
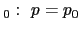 , e a
hipótese alternativa H
, e a
hipótese alternativa H
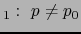 .
.
- Calcule a proporção amostral
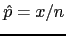 .
.
- Calcule o erro padrão, SE
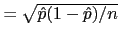 .
.
- Calcule
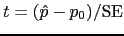 , o número de erros
padrão que
, o número de erros
padrão que 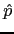 dista do valor de hipótese
dista do valor de hipótese 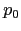 .
.
- Encontre o
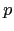 -valor usando o valor absoluto da estatística de
teste da tabela da distribuição normal (ou equivalentemente da
-valor usando o valor absoluto da estatística de
teste da tabela da distribuição normal (ou equivalentemente da
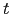 com
com 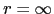 graus de liberdade).
graus de liberdade).
Uma regra geral é que este teste é válido quando
quando temos ambos 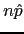 e
e 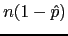 maiores do que
digamos 10.
maiores do que
digamos 10.
Exemplo:
Suponha que alguém tenha sugerido de experiências passadas que 60%
das larvas de mosquito num certo lago deveriam ser da espécie Aedes detritus. Foram encontrados
60 desse tipo de uma amostra de 80. Os dados suportam esta hipóteste?
Exercício
- Um amigo sugere que você lance uma moeda para ajudar você a
tomar uma decisão muito importante, o resultado também o
afetará. Seu amigo sugere que você escolha cara para tomar a decisão
A, e coroa para tomar a decisão B a qual é a preferida por ele. O
único problema é que seu amigo insiste que você use uma moeda ``da
sorte'' dele. Você fica um pouco suspeito e decide fazer um
experimento enquanto seu amigo não está olhando. Você lança a moeda
40 vezes e cara aparece somente 13 vezes. Realize um teste estatístico para ajudá-lo na decisão se você deve ou não acreditar que a moeda é balanceada. Qual a sua conclusão?
- Suponha que estejamos interessados em estimar a proporção de
todos os motoristas que excedem o limite máximo de velocidade num
trecho da rodovia entre Curitiba-São Paulo. Quão grande deve ser a
amostra para que estejamos pelo menos 99% confiantes de que o erro
de nossa estimativa, a proporção amostral, seja no máximo 0.04?
- Refaça o exercício anterior, sabendo que temos boas razões para
acreditar que a proporção que estamos tentando estimar é no mínimo
0.65.
shimakur
2016-02-29
![]() para uma
proporção. Podemos realisar um teste de H
para uma
proporção. Podemos realisar um teste de H![]() praticamente da mesma forma que o test-t acima. A
dualidade com intervalos de confiança segue exatamente da mesma
forma.
praticamente da mesma forma que o test-t acima. A
dualidade com intervalos de confiança segue exatamente da mesma
forma.
![]() de uma
população de interesse onde a verdadeira proporção de membros numa
categoria em particular é
de uma
população de interesse onde a verdadeira proporção de membros numa
categoria em particular é ![]() . A hipótese nula é H
. A hipótese nula é H![]() .
Se o número observado na categoria de interesse é
.
Se o número observado na categoria de interesse é ![]() , então um teste
da hipótese é como segue:
, então um teste
da hipótese é como segue: