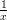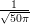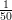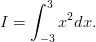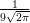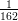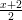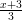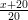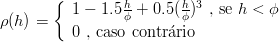6 Miscelânia de funcionalidades do R
6.1 O R como calculadora
Podemos fazer algumas operações matemáticas simples utilizando o R. Vejamos alguns exemplos
calculando as seguintes somas:
-
(a)
- 102 + 112 + … + 202
Para obter a resposta devemos
- criar uma sequência de números de 10 a 20
- elevar ao quadrado cada valor deste vetor
- somar os elementos do vetor
E estes passos correspondem aos seguintes comandos
[1] 10 11 12 13 14 15 16 17 18 19 20
[1] 100 121 144 169 196 225 256 289 324 361 400
Note que só precisamos do último comando para obter a resposta, mas é sempre útil entender os
comandos passo a passo!
-
(b)
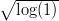 +
+ 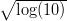 +
+ 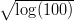 + … +
+ … + 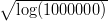 ,
,
onde log é o logarítmo neperiano. Agora vamos resolver com apenas um comando:
> sum(sqrt(log(10^(0:6))))
6.2 Gráficos de funções
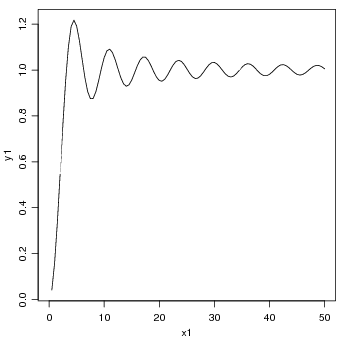
Para ilustrar como podemos fazer gráficos de funções vamos considerar cada uma das funções a seguir
cujos gráficos são mostrados nas Figuras 6.2 e 6.2.
-
(a)
- f(x) = 1 -
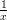 sin(x) para 0 ≤ x ≤ 50
sin(x) para 0 ≤ x ≤ 50
-
(b)
- f(x) =
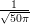 exp[-
exp[-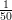 (x - 100)2] para 85 ≤ x ≤ 115
(x - 100)2] para 85 ≤ x ≤ 115
A idéia básica é criar um vetor com valores das abscissas (valores de x) e calcular o valor da
função (valores de f(x)) para cada elemento da função e depois fazer o gráfico unindo os pares de
pontos. Vejamos os comandos para o primeiro exemplo.
> x1 <- seq(0, 50, l = 101)
> y1 <- 1 - (1/x1) * sin(x1)
> plot(x1, y1, type = "l")
Note que este procedimento é o mesmo que aprendemos para fazer esboços de gráficos a mão em uma
folha de papel!
Há ainda uma outra maneira de fazer isto no R utilizando plot.function() conforme pode ser
visto no comando abaixo que nada mais faz que combinar os três comandos acima em apenas um.
> plot(function(x) 1 - (1/x) * sin(x), 0, 50)
Vejamos agora como obter o gráfico para a segunda função.
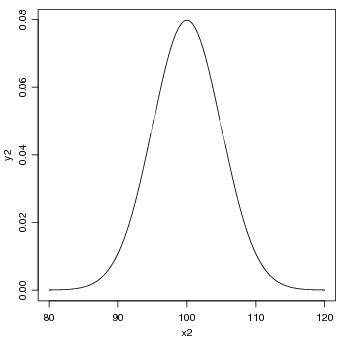
> x2 <- seq(80, 120, l = 101)
> y2 <- (1/sqrt(50 * pi)) * exp(-0.02 * (x2 - 100)^2)
> plot(x2, y2, type = "l")
Note ainda que esta função é a densidade da distribuição normal e o gráfico também poderia ser
obtido com:
> y2 <- dnorm(x2, 100, 5)
> plot(x2, y2, type = "l")
ou ainda:
> plot(function(x) dnorm(x, 100, 5), 85, 115)
6.3 Integração numérica
A função integrate() é usada para integração numérica em uma dimensão. Como exemplo vamos
considerar resolver a seguinte integral:
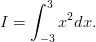 | (2) |
Para resolver a integral devemos criar uma função no R com a expressão da função que vamos integrar
e esta deve ser passada para integrate() conforme este exemplo:
> fx <- function(x) x^2
> integrate(fx, -3, 3)
18 with absolute error < 2e-13
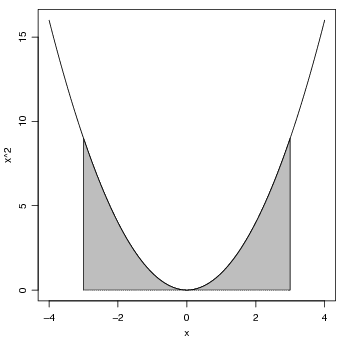
A integral acima corresponde à área mostrada no gráfico da Figura 6.3. Esta figura é obtida com os
seguinte comandos:
> x <- seq(-4, 4, l = 100)
> x2 <- x^2
> plot(x, x^2, ty = "l")
> x <- seq(-3, 3, l = 100)
> x2 <- x^2
> polygon(rbind(cbind(rev(x), 0), cbind(x, x2)), col = "gray")
Vejamos mais um exemplo. Sabemos que para distribuições contínuas de probabilidades a integral
está associada a probabilidade em um intervalo. Seja f(x) uma f.d.p. de uma variável contínua, então
P(a < X < b) = ∫
abf(x)dx. Por exemplo, seja X v.a. com distribuição N(100, 81) e portanto
f(x) = 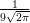 exp{-
exp{-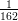 (x - 100)2}. A probabilidade P(85 < X < 105) pode ser calculada das
três formas diferentes que irão retornar os memos resultados conforma mostrado a seguir.
(x - 100)2}. A probabilidade P(85 < X < 105) pode ser calculada das
três formas diferentes que irão retornar os memos resultados conforma mostrado a seguir.
> fx <- function(x) {
+ (1/(9 * sqrt(2 * pi))) * exp(-(1/162) * (x - 100)^2)
+ }
> integrate(fx, 85, 105)
0.6629523 with absolute error < 7.4e-15
> integrate(function(x) dnorm(x, 100, 9), 85, 105)
0.6629523 with absolute error < 7.4e-15
> pnorm(105, 100, 9) - pnorm(85, 100, 9)
6.4 Matemática simbólica no R
Embora o R seja um programa predominantemente para operações numéricas, é possivel
obter alguns resultados simbólicos, em particular para expressões de derivadas que podem
ser informadas para algorítimos de otimização numérica. A forma básica de utilização
consiste em: (i) defina a expressão desejada dentro de quote(), (ii) use D() para obter a
expressão da derivada desejada informando a expressão e o termo em relação ao qual
deseja-se derivar a expressão, (iii) use eval() caso queira obter o valor numérico de uma
determinada expressão. A documentação help(D) fornece mais detalhes. Vejamos um exemplo.
> f <- quote(sin(x^2 + log(y + z)))
> f
> df.dx <- D(f, "x")
> df.dx
cos(x^2 + log(y + z)) * (2 * x)
> df.dy <- D(f, "y")
> df.dy
cos(x^2 + log(y + z)) * (1/(y + z))
> eval(f, list(x = 1, y = 2, z = 3))
> eval(df.dx, list(x = 1, y = 2, z = 3))
Existem programas computacionais especializados em matemática simbólica dentre os quais
destacam-se os projetos axiom, maxima e yacas.
Todos estes programas estão disponíveis para várias plataformas/sistemas operacionais. Também
estão incluídos nas distribuições de sistemas LINUX podendo ser instalados a partir de versões
pré-compiladas. Alguns ainda oferecem interfaces gráficas.
Para o YACAS e PYTON-SYMPY há os pacotes do R Ryacas e rSymPy que permitem acessar
suas funcionalidades diretamente de dentro de uma sessão.
6.5 Exercícios
-
1.
- Calcule o valor das expressões abaixo
-
(a)
- Seja x = (12, 11, 14, 15, 10, 11, 14, 11).
Calcule E = -nλ+(∑
1nx
i) log(λ)-∑
1n log(x
i!), onde n é o número de elementos
do vetor x e λ = 10.
Dica: o fatorial de um número pode ser obtido utilizando a função prod. Por exemplo
o valor de 5! é obtido com o comando prod(1:5).
Há ainda uma outra forma usando a função Gama e lembrando que para a inteiro,
Γ(a + 1) = a!. Portanto podemos obter o valor de 5! com o comando gamma(6).
-
(b)
- E = (π)2 + (2π)2 + (3π)2 + … + (10π)2
-
(c)
- E = log(x + 1) + log(
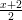 ) + log(
) + log(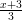 ) + … + log(
) + … + log(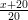 ), para x = 10
), para x = 10
-
2.
- Obtenha o gráfico das seguintes funções:
-
(a)
- f(x) = x12(1 - x)8 para 0 < x < 1
-
(b)
- Para ϕ = 4,
-
3.
- Considerando as funções acima calcule as integrais a seguir e indique a área correspondente nos
gráficos das funções.
-
(a)
- I1 = ∫
0.20.6f(x)dx
-
(b)
- I2 = ∫
1.53.5ρ(h)dh
-
4.
- Mostre os comandos para obter as seguintes sequências de números
-
(a)
- 1 11 21 31 41 51 61 71 81 91
-
(b)
- 1 1 2 2 2 2 2 3 3 3
-
(c)
- 1.5 2.0 2.5 3.0 3.5 1.5 2.0 2.5 3.0 3.5 1.5 2.0 2.5 3.0 3.5
-
5.
- Escreva a sequência de comandos para obter um gráfico x versus y, onde x é um vetor com 100
valores igualmente espaçados no intervalo [-1, 1] e y = sin(x) * exp(-x).
-
6.
- Escreva uma sequência de comandos no R para calcular a soma dos 80 primeiros termos das
séries:
-
(a)
- 1 + 1∕32 + 1∕52 + 1∕72 + 1∕92 + …
-
(b)
- 1 - 1∕22 + 1∕32 - 1∕42 + 1∕52 - 1∕62 + …
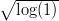 +
+ 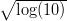 +
+ 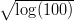 + … +
+ … + 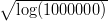 ,
,