28 Usando simulação para ilustrar resultados

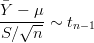
Podemos utilizar recursos computacionais e em particular simulações para inferir distribuições amostrais de quantidades de interesse. Na teoria de estatística existem vários resultados que podem ser ilustrados via simulação, o que ajuda na compreensão e visualização dos conceitos e resultados. Veremos alguns exemplos a seguir.

Este uso de simulações é apenas um ponto de partida pois estas são especialmente úteis para explorar situações onde resultados teóricos não são conhecidos ou não podem ser obtidos.

28.1 Relações entre a distribuição normal e a χ²

Resultado 1: Se Z ~ N(0, 1) então Z² ~ χ ₍₁₎².

Vejamos como ilustrar este resultado. Inicialmente vamos definir o valor da semente de números aleatórios para que os resultados possam ser reproduzidos. Vamos começar gerando uma amostra de 1000 números da distribuição normal padrão. A seguir vamos fazer um histograma dos dados obtidos e sobrepor a curva da distribuição teórica. Fazemos isto com os comando abaixo e o resultado está no gráfico da esquerda da Figura 73.

Note que, para fazer a comparação do histograma e da curva teórica é necessário que o histograma seja de frequências relativas e para isto usamos o argumento prob = T.

Agora vamos estudar o comportamento do quadrado da variável. O gráfico da direita da Figura 73 mostra o histograma dos quadrados do valores da amostra e a curva da distribuição de χ₍₁₎².

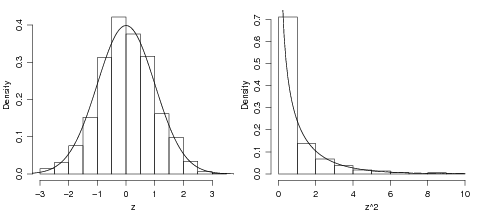
Nos gráficos anteriores comparamos o histograma da distribuição empírica obtida por simulação com a curva teórica da distribuição. Uma outra forma e mais eficaz forma de comparar distribuições empíricas e teóricas é comparar os quantis das distribuições e para isto utilizamos o qq-plot. O qq-plot é um gráfico dos dados ordenados contra os quantis esperados de uma certa distribuição. Quanto mais próximo os pontos estiverem da bissetriz do primeiro quadrante mais próximos os dados observados estão da distribuição considerada. Portanto para fazer o qqplot seguimos os passos:

1.

obter os dados,

2.

obter os quantis da distribuição teórica,

3.

fazer um gráfico dos dados ordenados contra os quantis da distribuição.

Vamos ilustrar isto nos comandos abaixo. Primeiro vamos considerar como dados os quadrados da amostra da normal obtida acima. Depois obtemos os quantis teóricos da distribução χ² usando a função qchisq em um conjunto de probabilidades geradas pela função ppoints. Por fim usamos a função qqplot para obter o gráfico mostrado na Figura 74, adicionando neste gráfico a bissetriz do primeiro quadrante para facilitar a avaliação do ajuste.

Note que o comando qchisq(ppoints(length(z)), df=1) acima está concatenando 3 comandos e calcula os quantis da χ² a partir de uma sequência de valores de probabilidade gerada por ppoints. O número de elementos desta sequência deve igual ao número de dados e por isto usamos length(z).

Resultado 2: Se Z₁,Z₂,…Z_n ~ N(0, 1) então ∑ ₁ⁿZ _i² ~ χ _(n)².

Para ilustrar este resultado vamos gerar 10.000 amostras de 3 elementos cada da distribuiçâo normal padrão, elevar os valores ao quadrado e, para cada amostra, somar os quadrados dos três números. Na Figura 75 mostramos no gráfico à esquerda, o histograma dos valores obtidos com a curva da distribuição esperada e no da direita o qq-plot para a distribuição χ₍₃₎².

28.2 Distribuição amostral da média de amostras da distribuição normal

Resultado 3: Se Y ₁,Y ₂,…Y _n ~ N(μ,σ²) então y ~ N(μ,σ²∕n).

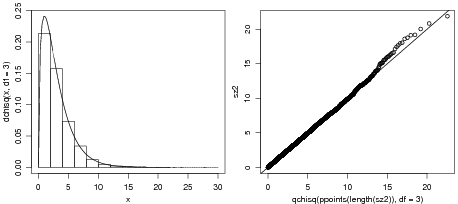
Neste exemplo vamos obter 1000 amostras de tamanho 20 de uma distribuição normal de média 100 e variância 30. Vamos organizar as amostras em uma matriz onde cada coluna corresponde a uma amostra. A seguir vamos calcular a média de cada amostra.

Pelo Resultado 3 acima esperamos que a média das médias amostrais seja 100 e a variância seja 1.5 (= 30/20), e que a distribuição das médias amostrais seja normal, valores bem próximos dos obtidos acima, sendo que as diferenças são devidas ao erro de simulação pro trabalharmos com amostras de tamanho finito. Para completar vamos obter o gráfico com o histograma das médias das amostras e a distribuição teórica conforme Figura 76 e o respectivo qq-plot.

Note que para obter o qq-plot neste exemplo utilizamos as funções qqnorm qqline já disponíveis no R para fazer qq-plot para distribuição normal.

28.3 Exercícios

1.

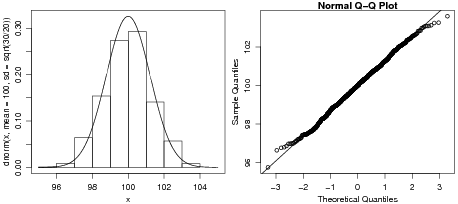
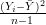Ilustrar usando simulação o resultado que afirma que para o estimador S² = ∑ da variância de uma distribuição normal, a variável V = (n - 1)S²∕σ² tem distribuição χ_n-1².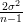
DICA: Voce pode começar pensando nos passos necessários para ilustrar este resultado:

• escolha os parâmetros de uma distribuição normal,
• escolha o tamanho de amostra n e o número de simulações N,
• gere N amostras de tamanho n,
• para cada amostra calcule S² e V = (n - 1)S²∕σ²,
• faça um histograma com os valores V e compare com a curva de uma distribuição χ_n-1².

2.

No exercício anterior compare os valores teóricos E[S²] = σ² e V ar[S²] = com os valores obtidos na simulação.

3.

Considere uma distribuição normal de média μ = 0 e variância unitária e amostras de tamanho n = 20 desta distribuição. Considere agora dois estimadores: T₁ = (x), a média da amostra e T₂ = md(x), a mediana na amostra. Avalie e compare através de simulações a eficiência dos dois estimadores. É possível identificar o mais eficiente? Qual a eficiência relativa? Repita o procedimento com diferentes tamanhos de amostra e verifique o efeito do tamanho da amostra na eficiência relativa.

4.

Seja Y ₁,…,Y _n a.a. de uma distribuição N(μ,σ²). Ilustrar o resultado que justifica o teste-t para média de uma amostra, onde S é o desvio padrão da amostra e n o tamanho da amostra.
DICA: começe verificando passo a passo, como no exercício anterior, o que é necessário para ilustrar este resultado.

5.

Ilustrar o resultado que diz que o quociente de duas variáveis independentes com distribuição χ² tem distribuição F.