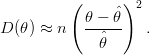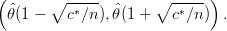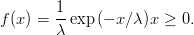18 Intervalos de confiança baseados na deviance
Neste sessão discutiremos a obtenção de intervalos de confiança baseado na função
deviance.
18.1 Média da distribuição normal com variância conhecida
Seja X1,…,Xn a.a. de uma distribuição normal de média θ e variância 1. Vimos que:
-
1.
- A função de log-verossimilhança é dada por l(θ) = cte +
 ∑
i=1n(x
i - θ)2;
∑
i=1n(x
i - θ)2;
-
2.
- o estimador de máxima verossimilhança é
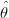 =
= 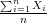 = X;
= X;
-
3.
- a função deviance é D(θ) = n(x - θ)2;
-
4.
- e neste caso a deviance tem distribuição exata χ(1)2;
-
5.
- e os limites do intervalo são dados por x
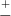
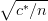 , onde c* é o quantil (1 - α∕2) da
distribuição χ(1)2.
, onde c* é o quantil (1 - α∕2) da
distribuição χ(1)2.
Vamos considerar que temos uma amostra onde n = 20 e x = 32. Neste caso a função deviance é
como mostrada na Figura 40 que é obtida com os comandos abaixo onde primeiro definimos uma
função para calcular a deviance que depois é mostrada em um gráfico para valores entre 30 e 34. Para
obtermos um intervalo a 95% de confiança escolhemos o quantil correspondente na distribuição χ(1)2 e
mostrado pela linha tracejada no gráfico. Os pontos onde esta linha cortam a função são, neste
exemplo, determinados analiticamente pela expressão dada acima e indicados pelos setas verticais no
gráfico.
> dev.norm.v1 <- function(theta, n, xbar) {
+ n * (xbar - theta)^2
+ }
> thetaN.vals <- seq(31, 33, l = 101)
> dev.vals <- dev.norm.v1(thetaN.vals, n = 20, xbar = 32)
> plot(thetaN.vals, dev.vals, ty = "l", xlab = expression(theta),
+ ylab = expression(D(theta)))
> L.95 <- qchisq(0.95, df = 1)
> abline(h = L.95, lty = 3)
> IC <- 32 + c(-1, 1) * sqrt(L.95/20)
> IC
> arrows(IC, rep(L.95, 2), IC, rep(0, 2), length = 0.1)
Vamos agora examinar o efeito do tamanho da amostra na função. A Figura 41 mostra as funções
para três tamanhos de amostra, n = 10, 20 e 50 que são obtidas com os comandos abaixo. A linha
horizontal mostra o efeito nas amplitudes dos IC’s.
> L.95 <- qchisq(0.95, df = 1)
> dev10.vals <- dev.norm.v1(thetaN.vals, n = 10, xbar = 32)
> plot(thetaN.vals, dev10.vals, ty = "l", xlab = expression(theta),
+ ylab = expression(D(theta)))
> IC10 <- 32 + c(-1, 1) * sqrt(L.95/10)
> arrows(IC10, rep(L.95, 2), IC10, rep(0, 2), length = 0.1)
> dev20.vals <- dev.norm.v1(thetaN.vals, n = 20, xbar = 32)
> lines(thetaN.vals, dev20.vals, lty = 2)
> IC20 <- 32 + c(-1, 1) * sqrt(L.95/20)
> arrows(IC20, rep(L.95, 2), IC20, rep(0, 2), length = 0.1, lty = 2)
> dev50.vals <- dev.norm.v1(thetaN.vals, n = 50, xbar = 32)
> lines(thetaN.vals, dev50.vals, lwd = 2)
> IC50 <- 32 + c(-1, 1) * sqrt(L.95/50)
> arrows(IC50, rep(L.95, 2), IC50, rep(0, 2), length = 0.1, lwd = 2)
> abline(h = qchisq(0.95, df = 1), lty = 3)
> legend(31, 2, c("n=10", "n=20", "n=50"), lty = c(1, 2, 1), lwd = c(1,
+ 1, 2), cex = 0.7)
18.2 IC para o parâmetro da distribuição exponencial
Seja x1,…,xn a.a. de uma distribuição exponencial de parâmetro θ com função de densidade
f(x) = θ exp{-θx}. Vimos que:
-
1.
- A função de log-verossimilhança é dada por l(θ) = n log(θ) - θnx;
-
2.
- o estimador de máxima verossimilhança é
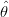 =
= 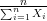 =
= 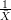 ;
;
-
3.
- a função deviance é D(θ) = 2n
![[ ]
log (ˆθ∕θ) + ¯x(θ - ˆθ)](Rembrapa115x.png) ;
;
-
4.
- e neste caso a deviance tem distribuição assintótica χ(1)2;
-
5.
- e os limites do intervalo não podem ser obtidos analiticamente, devendo ser obtidos
por:
- métodos numéricos ou gráficos, ou,
- pela aproximação quadrática da verossimilhança por série de Taylor que neste caso
fornece uma expressão da deviance aproximada dada por D(θ) ≈ n
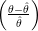 2.
2.
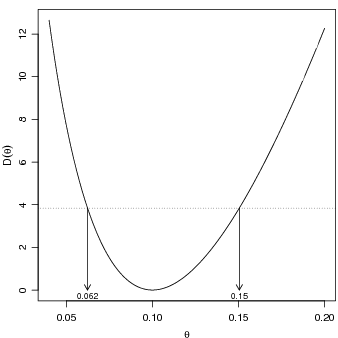
A seguir vamos ilustrar a obtenção destes intervalos no R. Vamos considerar que temos uma
amostra onde n = 20 e x = 10 para a qual a função deviance é mostrada na Figura 42 e obtida de
forma análoga ao exemplo anterior. O estimador de máxima verossimilhança pode ser obtido
analiticamente neste exemplo 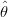 = 1∕x = 1∕10 = 0.1.
= 1∕x = 1∕10 = 0.1.
> dev.exp <- function(theta, n, xbar) {
+ 2 * n * (log((1/xbar)/theta) + xbar * (theta - (1/xbar)))
+ }
> thetaE.vals <- seq(0.04, 0.2, l = 101)
> dev.vals <- dev.exp(thetaE.vals, n = 20, xbar = 10)
> plot(thetaE.vals, dev.vals, ty = "l", xlab = expression(theta),
+ ylab = expression(D(theta)))
Neste exemplo, diferentemente do anterior, não determinamos a distribuição exata da deviance e
usamos a distribuição assintótica χ(1)2 na qual se baseia a linha de corte tracejada mostrada no
gráfico para definir o IC do parâmetro ao nível de 95% de confiança.
Para encontrar os limites do IC precisamos dos valores no eixo dos parâmetros nos
pontos onde a linha de corte toca a função deviance o que corresponde a resolver a equação
D(θ) = 2n![[ ]
log(ˆθ∕θ) + ¯x(θ - ˆθ)](Rembrapa119x.png) = c* onde c* é quantil da distribuição da χ2 com 1 grau de
liberdade correspondente ao nível de confiança desejado. Por exemplo, para 95% o valor de
χ1,0.952 é 3.84. Como, diferentemente do exemplo anterior, esta equação não tem solução
analítica vamos examinar a seguir duas possíveis soluções para encontrar os limites do
intervalo.
= c* onde c* é quantil da distribuição da χ2 com 1 grau de
liberdade correspondente ao nível de confiança desejado. Por exemplo, para 95% o valor de
χ1,0.952 é 3.84. Como, diferentemente do exemplo anterior, esta equação não tem solução
analítica vamos examinar a seguir duas possíveis soluções para encontrar os limites do
intervalo.
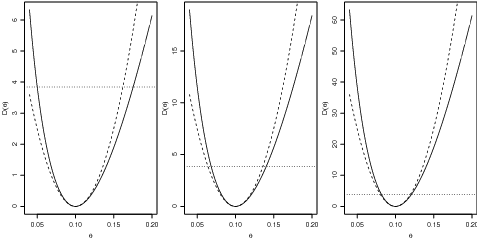
18.2.1 Solução numérica/gráfica simplificada
Iremos aqui considerar uma solução simples baseada no gráfico da função deviance para encontrar os
limites do IC que consiste no seguinte: Para fazermos o gráfico da deviance criamos uma
sequência de valores do parâmetro θ. A cada um destes valores corresponde um valor de
D(θ). Vamos então localizar os valores de θ para os quais D(θ) é o mais próximo possível
do ponto de corte. Isto é feito com o código abaixo e o resultado exibido na Figura 43.
> plot(thetaE.vals, dev.vals, ty = "l", xlab = expression(theta),
+ ylab = expression(D(theta)))
> L.95 <- qchisq(0.95, df = 1)
> abline(h = L.95, lty = 3)
> dif <- abs(dev.vals - L.95)
> theta.est <- 1/10
> lim.fc <- function(x) dev.exp(x, n = 20, xbar = 10) - L.95
> ICdev <- c(uniroot(lim.fc, c(0, theta.est))$root, uniroot(lim.fc,
+ c(theta.est, 1))$root)
> arrows(ICdev, rep(L.95, 2), ICdev, rep(0, 2), len = 0.1)
> text(ICdev, 0, round(ICdev, dig = 3), pos = 1, cex = 0.8, offset = 0.3)
Note que neste código procuramos primeiro o limite inferior entre os valores menores que a
estimativa do parâmetro (1/10) e depois o limite superior entre os valores maiores que esta estimativa.
Para isto usamos a função uniroot() que fornece raízes unidimensionais de uma função que
definimos como a diferença entre a função deviançe e o valor de corte definido pela distribuição χ2
para o nível de significância desejado.
18.2.2 Aproximação quadrática da verossimilhança
Nesta abordagem aproximamos a função deviance por uma função quadrática obtida pela expansão
por série de Taylor ao redor do estimador de máxima verossimilhança:
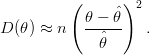 A
Figura 44 obtida com os comandos mostra o gráfico desta função deviance aproximada. A
Figura também mostra os IC’s obtido com esta função. Para a aproximação quadrática
os limites dos intervalos são facilmente determinados analiticamente e neste caso dados
por:
A
Figura 44 obtida com os comandos mostra o gráfico desta função deviance aproximada. A
Figura também mostra os IC’s obtido com esta função. Para a aproximação quadrática
os limites dos intervalos são facilmente determinados analiticamente e neste caso dados
por:
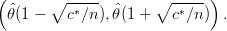
> devap.exp <- function(theta, n, xbar) {
+ n * (xbar * (theta - (1/xbar)))^2
+ }
> devap.vals <- devap.exp(thetaE.vals, n = 20, xbar = 10)
> plot(thetaE.vals, devap.vals, ty = "l", xlab = expression(theta),
+ ylab = expression(D(theta)))
> L.95 <- qchisq(0.95, df = 1)
> abline(h = L.95, lty = 3)
> ICdevap <- (1/10) * (1 + c(-1, 1) * sqrt(L.95/20))
> ICdevap
[1] 0.05617387 0.14382613
> arrows(ICdevap, rep(L.95, 2), ICdevap, rep(0, 2), len = 0.1)
> text(ICdevap, 0, round(ICdev, dig = 3), pos = 1, cex = 0.8, offset = 0.3)
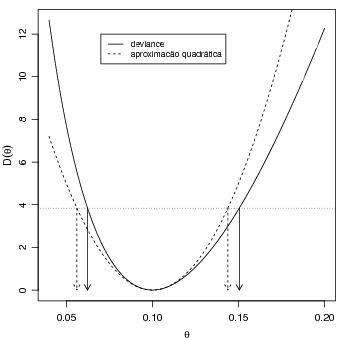
18.3 Comparando as duas estratégias
Examinando os limites dos intervalos encontrados anteriormente podemos ver que são diferentes.
Vamos agora colocar os resultados pelos dois métodos em um mesmo gráfico (Figura 45) para
comparar os resultados.
> plot(thetaE.vals, dev.vals, ty = "l", xlab = expression(theta),
+ ylab = expression(D(theta)))
> lines(thetaE.vals, devap.vals, lty = 2)
> abline(h = L.95, lty = 3)
> arrows(ICdev, rep(L.95, 2), ICdev, rep(0, 2), len = 0.1)
> arrows(ICdevap, rep(L.95, 2), ICdevap, rep(0, 2), lty = 2, len = 0.1)
> legend(0.07, 12, c("deviance", "aproximacão quadrática"), lty = c(1,
+ 2), cex = 0.8)
Vamos agora examinar o efeito do tamanho da amostra na função deviance e sua aproximação
quadrática. A Figura 46 mostra as funções para três tamanhos de amostra, n = 10, 30 e 100 que são
obtidas com os comandos abaixo onde vemos que a aproximação fica cada vez melhor com o aumento
do tamanho da amostra.
> thetaE.vals <- seq(0.04, 0.2, l = 101)
> dev10.vals <- dev.exp(thetaE.vals, n = 10, xbar = 10)
> plot(thetaE.vals, dev10.vals, ty = "l", xlab = expression(theta),
+ ylab = expression(D(theta)))
> devap10.vals <- devap.exp(thetaE.vals, n = 10, xbar = 10)
> lines(thetaE.vals, devap10.vals, lty = 2)
> abline(h = qchisq(0.95, df = 1), lty = 3)
> dev30.vals <- dev.exp(thetaE.vals, n = 30, xbar = 10)
> plot(thetaE.vals, dev30.vals, ty = "l", xlab = expression(theta),
+ ylab = expression(D(theta)))
> devap30.vals <- devap.exp(thetaE.vals, n = 30, xbar = 10)
> lines(thetaE.vals, devap30.vals, lty = 2)
> abline(h = qchisq(0.95, df = 1), lty = 3)
> dev100.vals <- dev.exp(thetaE.vals, n = 100, xbar = 10)
> plot(thetaE.vals, dev100.vals, ty = "l", xlab = expression(theta),
+ ylab = expression(D(theta)))
> devap100.vals <- devap.exp(thetaE.vals, n = 100, xbar = 10)
> lines(thetaE.vals, devap100.vals, lty = 2)
> abline(h = qchisq(0.95, df = 1), lty = 3)
18.4 Exercícios
-
1.
- Seja 14.1, 30.0, 19.6, 28.2, 12.5, 15.2, 17.1, 11.0, 25.9, 13.2, 22.8, 22.1 a.a. de uma distribuição
normal de média 20 e variância σ2.
-
(a)
- Obtenha a função deviance para σ2 e faça o seu gráfico.
-
(b)
- Obtenha a função deviance para σ e faça o seu gráfico.
-
(c)
- Obtenha os IC’s a 90% de confiança.
-
2.
- Repita as análises mostradas no exemplo acima da distribuição exponencial mas agora
utilizando a seguinte parametrização para a função de densidade:
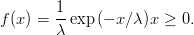 Discuta as diferenças entre os resultados obtidos nas duas parametrizações.
Discuta as diferenças entre os resultados obtidos nas duas parametrizações.
 ∑
i=1n(x
i - θ)2;
∑
i=1n(x
i - θ)2;
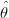 =
= 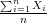 = ;
= ;
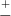
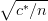 , onde c* é o quantil (1 - α∕2) da
distribuição χ(1)2.
, onde c* é o quantil (1 - α∕2) da
distribuição χ(1)2. ∑
i=1n(x
i - θ)2;
∑
i=1n(x
i - θ)2;
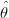 =
= 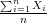 = ;
= ;
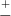
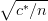 , onde c* é o quantil (1 - α∕2) da
distribuição χ(1)2.
, onde c* é o quantil (1 - α∕2) da
distribuição χ(1)2.
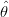 =
= 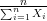 =
= 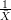 ;
;
![[ ]
log (ˆθ∕θ) + ¯x(θ - ˆθ)](Rembrapa115x.png) ;
;
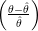 2.
2.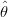 = 1∕ = 1∕10 = 0.1.
= 1∕ = 1∕10 = 0.1.
![[ ]
log(ˆθ∕θ) + ¯x(θ - ˆθ)](Rembrapa119x.png) = c* onde c* é quantil da distribuição da χ2 com 1 grau de
liberdade correspondente ao nível de confiança desejado. Por exemplo, para 95% o valor de
χ1,0.952 é 3.84. Como, diferentemente do exemplo anterior, esta equação não tem solução
analítica vamos examinar a seguir duas possíveis soluções para encontrar os limites do
intervalo.
= c* onde c* é quantil da distribuição da χ2 com 1 grau de
liberdade correspondente ao nível de confiança desejado. Por exemplo, para 95% o valor de
χ1,0.952 é 3.84. Como, diferentemente do exemplo anterior, esta equação não tem solução
analítica vamos examinar a seguir duas possíveis soluções para encontrar os limites do
intervalo.