8 Intervalos de confiança e testes de hipótese

Nesta sessão vamos verificar como utilizar o R para obter intervalos de confiança e testar hipóteses sobre parâmetros de interesse.

8.1 Média de uma distribuição normal com variância desconhecida

Considere resolver o seguinte problema:

Exemplo
O tempo de reação de um novo medicamento pode ser considerado como tendo distribuição Normal e deseja-se fazer inferência sobre a média que é desconhecida obtendo um intervalo de confiança. Vinte pacientes foram sorteados e tiveram seu tempo de reação anotado. Os dados foram os seguintes (em minutos):

2.9	3.4	3.5	4.1	4.6	4.7	4.5	3.8	5.3	4.9
4.8	5.7	5.8	5.0	3.4	5.9	6.3	4.6	5.5	6.2

Neste primeiro exemplo, para fins didáticos vamos mostrar duas possíveis soluções:

1. fazendo as contas passo a passo, utilizando o R como uma calculadora
2. usando uma função já existente no R

Entramos com os dados com o comando

> tempo <- c(2.9, 3.4, 3.5, 4.1, 4.6, 4.7, 4.5, 3.8, 5.3, 4.9,
             4.8, 5.7, 5.8, 5.0, 3.4, 5.9, 6.3, 4.6, 5.5, 6.2)

Sabemos que o intervalo de confiança para média de uma distribuição normal com média desconhecida é dado por:

$$\left(\bar{x} - t_{\alpha/2} \sqrt{\frac{S^2}{n}}\;\;\;,\;\;\; \bar{x} + t_{1 - \alpha/2} \sqrt{\frac{S^2}{n}} \right)$$

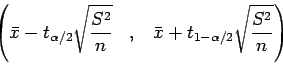
Vamos agora obter a resposta de duas formas diferentes.

8.1.1 Fazendo as contas passo a passo

Nos comandos a seguir calculamos o tamanho da amostra, a média e a variância amostral.

> n <- length(tempo)
> n
[1] 20 
> t.m <- mean(tempo)
> t.m
[1] 4.745
> t.v <- var(tempo)
> t.v
[1] 0.992079

A seguir montamos o intervalo utilizando os quantis da dritribuição $t$.

> t.ic <- t.m + qt(c(0.025, 0.975), df = n-1) * sqrt(t.v/length(tempo))
> t.ic
[1] 4.278843 5.211157

8.1.2 Usando a função t.test

Mostramos a solução acima para ilustrar a flexibilidade e o uso do programa. Entretanto não precisamos fazer isto na maioria das vezes porque o R já vem com várias funções para procedimentos estatísticos já escritas.

Para este exemplo específico

a função t.test pode ser utilizada como vemos no resultado do comando a sequir que coincide com os obtidos anteriormente.

> t.test(tempo)

        One Sample t-test

data:  tempo
t = 21.3048, df = 19, p-value = 1.006e-14
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 4.278843 5.211157
sample estimates:
mean of x
    4.745

O resultado da função mostra a estimativa obtida da média ($4.745$), o intervalo de confiança a 95e testa a igualdade de média a zero $(p-value = 1.006e-14)$, em um teste bilateral.

Os valores definidos no IC e teste de Hipótese acima são ``defaults'' que podem ser modificados. Por exemplo, para obter um IC a 99

> t.test(tempo, alt = "greater", mu = 3, conf.level = 0.99)

        One Sample t-test

data:  tempo
t = 7.835, df = 19, p-value = 1.140e-07
alternative hypothesis: true mean is greater than 3
99 percent confidence interval:
 4.179408      Inf
sample estimates:
mean of x
    4.745

8.2 Teste $\chi ^2$ de independência

Quando estudamos a relação entre duas variáveis qualitativas em geral fazemos uma tabela com o resultado do cruzamento desta variáveis. Em geral existe interesse em verificar se as variáveis estão associadas e para isto calcula-se uma medida de associação tal como o $\chi ^2$, coeficiente de contingência $C$, ou similar. O passo seguinte é testar se existe evidência que a associação é significativa. Uma possível forma de fazer isto é utilizando o teste $\chi ^2$.

Para ilustrar o teste vamos utilizar o conjunto de dados HairEyeColor que já vem disponível com o R. Para carregar e visualizar os dados use os comando abaixo.

> data(HairEyeColor)
> HairEyeColor
> as.data.frame(HairEyeColor)

Para saber mais sobre estes dados veja help(HairEyeColor) Note que estes dados já vem ``resumidos'' na forma de uma tabela de frequências tri-dimensional, com cada uma das dimensões .correspondendo a um dos atributos - cor dos cabelos, olhos e sexo.

Para ilustrar aqui o teste $\chi ^2$ vamos verificar se existe associação entre 2 atributos: cor dos olhos e cabelos entre os indivíduos do sexo feminino. Vamnos adotar $\alpha=5\%$ como nível de significância. Nos comandos abaixo primeiro isolamos apenas a tabela com os indivíduos do sexo masculino e depois aplicamos o teste sobre esta tabela.

> HairEyeColor[,,1]
       Eye
Hair    Brown Blue Hazel Green
  Black    32   11    10     3
  Brown    38   50    25    15
  Red      10   10     7     7
  Blond     3   30     5     8
> chisq.test(HairEyeColor[,,1])

        Pearson's Chi-squared test

data:  HairEyeColor[, , 1]
X-squared = 42.1633, df = 9, p-value = 3.068e-06

Warning message:
Chi-squared approximation may be incorrect in: chisq.test(HairEyeColor[, , 1])

O $p-value$ sugere que a associação é significativa. Entretanto este resultado deve ser visto com cautela pois a mensagem de alerta (Warning message) emitida pelo programa chama atenção ao fato de que há várias caselas com baixa frequência na tabela e portanto as condições para a validade do teste não são perfeitamente satisfeitas.

Uma possibilidade neste caso é então usar o $p-value$ calculado por simulação, ao invés do resultado assintótico usado no teste tradicional.

> chisq.test(HairEyeColor[,,1], sim=T)

        Pearson's Chi-squared test with simulated p-value (based on 2000
        replicates)

data:  HairEyeColor[, , 1]
X-squared = 42.1633, df = NA, p-value = 0.0004998

Note que agora a mensagem de alerta não é mais emitida e que a significância foi confirmada (P-valor < 0.05). Note que se voce rodar este exemplo poderá obter um $p-value$ um pouco diferente porque as simulações não necessariamente serão as mesmas.

Lembre-se de inspecionar help(chisq.test) para mais detalhes sobre a implementação deste teste no R.

8.3 Teste para o coeficiente de correlação linear de Pearson

Quando temos duas variáveis quantitativas podemos utilizar o coeficiente de correlação linear para medir a associação entre as variáveis, se a relação entre elas for linear. Para ilustrar o teste para o coeficiente linear de Pearson vamos estudar a relação entre o peso e rendimento de carros. Para isto vamos usar as variáveis wt (peso) e mpg (milhas por galão) do conjunto de dados mtcars.

> data(mtcars)
> attach(mtcars)
> cor(wt, mpg)
[1] -0.8676594
> cor.test(wt, mpg)

        Pearson's product-moment correlation

data:  wt and mpg
t = -9.559, df = 30, p-value = 1.294e-10
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.9338264 -0.7440872
sample estimates:
       cor
-0.8676594

> detach(mtcars)

Portanto o p-valor acima mmostra que a correlação encontrada de -0.87 difere significativamente de zero. Note que uma análise mais cuidadosa deveria incluir o exame do gráfico entre estas duas variáveis para ver se o coeficiente de correlação linear é adequado para medir a associação.

8.4 Comparação de duas médias

Quando temos uma variável qualitativa com dois níveis e outra quantitativa a análise em geral recai em comparar as médias da quantitativa para cada grupo da qualitativa. Para isto podemos utilizar o $teste T$. Há diferentes tipos de teste T: para amostras independentes ou pareadas, variâncias iguais ou desiguais.

Considere o seguinte exemplo:
Os dados a seguir correpondem a teores de um elemento indicador da qualidade de um certo produto vegetal. Foram coletadas 2 amostras referentes a 2 métodos de produção e deseja-se comparar as médias dos métodos fazendo-se um teste t bilateral, ao nível de 5% de significância e considerando-se as variâncias iguais.

Método 1	0.9	2.5	9.2	3.2	3.7	1.3	1.2	2.4	3.6	8.3
Método 2	5.3	6.3	5.5	3.6	4.1	2.7	2.0	1.5	5.1	3.5

> m1 <- c(0.9, 2.5, 9.2, 3.2, 3.7, 1.3, 1.2, 2.4, 3.6, 8.3)
> m2 <- c(5.3, 6.3, 5.5, 3.6, 4.1, 2.7, 2.0, 1.5, 5.1, 3.5)

 t.test(m1,m2, var.eq=T)

        Two Sample t-test

data:  m1 and m2
t = -0.3172, df = 18, p-value = 0.7547
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -2.515419  1.855419
sample estimates:
mean of x mean of y
     3.63      3.96

Os resultados mostram que não á evidências para rejeitar a hipótese de igualdade entre as médias.

8.5 Exercícios

1. Revisite os dados milsa visto na aula de estatística descritiva e selecione pares de variáveis adequadas para efetuar:
   1. um teste $\chi ^2$
   2. um teste para o coeficiente de correlação
   3. um teste t

2. Inspecione o conjunto de dados humanos.txt, selecione variáveis a aplique os testes vistos nesta Seção.

3. Queremos verificar se machos e fêmeas de uma mesma espécie possuem o mesmo comprimento (em $mm$) Para isso, foram medidos 6 exemplares de cada sexo e obtivemos os seguintes comprimentos:

   Machos	145	127	136	142	141	137
   Fêmeas	143	128	132	138	142	132

   Obtenha intervalos de confiança para a razão das variâncias e para a diferença das médias dos dois grupos.

   Dica: Use as funções var.test e t.test

4. Carregue o conjunto de dados iris usando o comando data(iris).
   Veja a descrição dos dados em help(iris).
   Use a função cor.test para testar a correlação entre o comprimento de sépalas e pétalas.