5 Funções de verossimilhança

A função de verossimilhança é central na inferência estatística. Nesta sessão vamos ver como traçar funções de verossimilhança utilizando o programa R.

5.1 Exemplo 1: Distribuição normal com variância conhecida

Seja o vetor $(12, 15, 9, 10, 17, 12, 11, 18, 15, 13)$ uma amostra aleatória de uma distribuição normal de média $\mu$ e variância conhecida e igual a $4$. O objetivo é fazer um gráfico da função de log-verossimilhança.

Solução:
Vejamos primeiro os passos da solução analítica:

1. Temos que $x_1, \ldots, x_n$ é uma a.a. de $X \sim N(\mu, 4)$,
2. a densidade para cada observação é dada por $f(x_i) = \frac{1}{2\sqrt{2\pi}} \exp\{\frac{1}{8}(x_i - \mu)^2\}$,
3. a verossimilhança é dada por $L(\mu) = \prod_1^{10} f(x_i)$,
4. e a log-verossimilhança é dada por

   $$\begin{eqnarray}\html{eqn0} \nonumber l(\mu) &=& \sum_1^{10} \log(f(x_i)) \\ ... ...\frac{1}{8} (\sum_1^{10}x_i^2 - 2\mu \sum_1^{10}x_i + 10\mu^2), \end{eqnarray}$$

   
   
5. que é uma função de $\mu$ e portanto devemos fazer um gráfico de $l(\mu)$ versus $\mu$ tomando vários valores de $\mu$ e calculando os valores de $l(\mu)$.

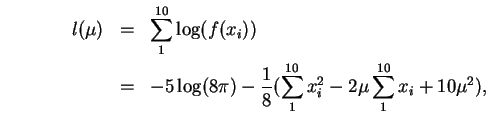
Vamos ver agora uma primeira possível forma de fazer a função de verossimilhança no R.

1. Primeiro entramos com os dados que armazenamos no vetor x

   > x <- c(12, 15, 9, 10, 17, 12, 11, 18, 15, 13)
   

2. e calculamos as quantidades $\sum_1^{10}x_i^2$ e $\sum_1^{10}x_i$

   > sx2 <- sum(x^2)
   > sx <- sum(x)
   

3. agora tomamos uma sequência de valores para $\mu$. Sabemos que o estimador de máxima verossimilhança neste caso é $\hat{\mu} = 13.2$ (este valor pode ser obtido com o comando mean(x)) e portanto vamos definir tomar valores ao redor deste ponto.

   > mu.vals <- seq(11, 15, l=100)
   

4. e a seguir calculamos os valores de $l(\mu)$ de acordo com a equação acima

   > lmu <- -5 * log(8*pi) - (sx2 - 2*mu.vals*sx + 10*(mu.vals^2))/8
   

5. e finalmente fazemos o gráfico visto na Figura 5

   > plot(mu.vals, lmu, type='l', xlab=expression(mu), ylab=expression(l(mu)))
   

Figura : Função de verossimilhança para o parâmetro $\mu$ da distribuição normal com variância $\sigma ^2=4$ com os dados do Exemplo 1.

Entretanto podemos obter a função de verossimilhança no R de outras forma mais geral e menos trabalhosas. Sabemos que a função dnorm calcula a densidade $f(x)$ da distribuição normal e podemos usar este fato para evitar a digitação da expressão acima.

• Primeiro vamos criar uma função que calcula o valor da log-verossimilhança para um certo valor do parâmetro e para um certo conjunto de dados,

  > logvero <- function(mu, dados){
       sum(dnorm(dados, mean = mu, sd = 2, log = TRUE))
    }
  

• a seguir criamos uma sequência adequada de valores de $\mu$ e calculamos $l(\mu)$ para cada um dos valores

  > mu.vals <- seq(11, 15, l=100)
  > mu.vals
  > lmu <- sapply(mu.vals, logvero, dados = x)
  > lmu
  

  Note na sintaxe acima que a função sapply aplica a função logvero anteriormente definida em cada elemento do vetor mu.vals.
• Finalmente fazemos o gráfico.

  > plot(mu.vals, lmu, type='l', xlab=expression(mu), ylab=expression(l(mu)))
  

Para encerrar este exemplo vamos apresentar uma solução ainda mais genérica que consiste em criar uma função que vamos chamar de vero.norm.v4 para cálculo da verossimilhança de distribuições normais com $\sigma^2$=4. Esta função engloba os comandos acima e pode ser utilizada para obter o gráfico da log-verossimilhança para o parâmetro $\mu$ para qualquer amostra obtida desta distribuição.

> vero.normal.v4 <- function(mu, dados){
    logvero <- function(mu, dados)
      sum(dnorm(dados, mean = mu, sd = 2, log = TRUE))
    sapply(mu, logvero, dados = dados)
  }
> curve(vero.normal.v4(x, dados = x), 11, 15, 
      xlab=expression(mu), ylab=expression(l(mu)))

5.2 Exercícios

1. Seja a amostra abaixo obtida de uma distribuição Poisson de parâmetro $\lambda$.
   5 4 6 2 2 4 5 3 3 0 1 7 6 5 3 6 5 3 7 2
   Obtenha o gráfico da função de log-verossimilhança.

2. Seja a amostra abaixo obtida de uma distribuição Binomial de parâmetro $p$ e com $n=10$.
   7 5 8 6 9 6 9 7 7 7 8 8 9 9 9
   Obtenha o gráfico da função de log-verossimilhança.

3. Seja a amostra abaixo obtida de uma distribuição $\chi^2$ de parâmetro $\nu$.
   8.9 10.1 12.1 6.4 12.4 16.9 10.5 9.9 10.8 11.4
   Obtenha o gráfico da função de log-verossimilhança.