Como funciona a ANOVA

Agora a ANOVA basicamente divide a variabilidade em variabilidade Entre Grupos e variabilidade Dentro de Grupos, e compara as duas.

Quanto maior for a primeira comparada à segunda, maior é a evidência de que existe variabilidade entre grupos, ou seja, médias diferentes.

Define-se a soma de quadrados total, SQT, como :

$$\mbox{\bf SQT} = \sum (x_i-\overline{x})^2,$$

calculada a partir de todos os dados, em que $\overline{x}$ é a média amostral global.

Note que a estimativa usual de variância de uma amostra é:

$$s^2 = \mbox{\bf SQT}/(n-1)$$

Podemos dividi-la como:

$$\mbox{\bf SQT} = \mbox{\bf SQD} + \mbox{\bf SQE},$$

em que

$$\mbox{\bf SQD} = \sum_{gp1} (x_i-\overline{x}_1)^2 +\sum_{gp2... ...gp3} (x_i-\overline{x}_3)^2 +\sum_{gp4} (x_i-\overline{x}_4)^2$$

e $\overline{x}_k$ é a média amostral do grupo $k$; e

$$\mbox{\bf SQE} = n_1 (\overline{x}_1 -\overline{x})^2 + n_2... ...x}_3 - \overline{x})^2 + n_4 (\overline{x}_4 - \overline{x})^2$$

em que $n_k$ é o tamanho amostral do grupo $k$.

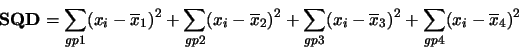
Aqui SQD é utilizado para denotar soma de quadrados dentro de grupo e SQE para a soma de quadrado entre grupos.

Agora tendo separado a variabilidade, é possivel mostrar que podemos obter estimativas independentes da variância populacional comum $\sigma^2$ a partir destas duas quantidades. Elas são chamadas de valores quadrados médios, e obtemos as seguintes estimativas:

$$s_1^2 = \mbox{\bf SQE}/(m-1),$$

$$s_2^2 = \mbox{\bf SQD}/(N-m),$$

em que $m$ é o número de grupos, e $N$ é o tamanho amostral total, aqui 20. Como estas estimativas de variância são construídas a partir de dois tipos diferentes de variabilidade, quanto mais elas diferirem, mais evidência existe de diferença nas médias.

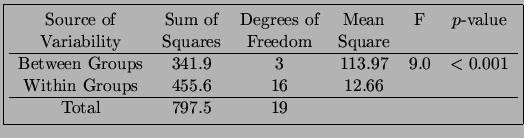
A estatística de teste é

$$F= s_1^2/s_2^2,$$

e comparamos este valor com uma distribuição F com $m-1$ e $N-m$ graus de liberdade para obter um $p$-valor. Sempre que uma ANOVA é feita é usual expressar os resultados numa tabela como segue:

Estes resultados são dos dados de estorninhos, e concluímos que existem evidências estatisticamente significativas ao nível de 5% de uma diferença nas médias de quatro situações de pousada diferentes.