6 3 5 4 4 4 6 3 1 6
Obter:
- (a)
- o estimador de máxima verossimilhança de theta
- (b)
- a informação de Fisher e a observada
- (c)
- um intervalo de confiança de 95% para
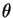 baseado na
normalidade assintótica de
baseado na
normalidade assintótica de 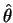
- (d)
- um intervalo de confiança de 95% par
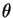 baseado na
distribuição limite da função deviance
baseado na
distribuição limite da função deviance
- (e)
- repita os itens (a)-(d) trocando
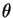 por
por 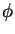 , onde
, onde
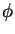 é a probabilidade de que não hajam trens atrasados num
particular dia
é a probabilidade de que não hajam trens atrasados num
particular dia
9.5 10.8 9.3 10.7 10.9 10.5 10.7 9.0 11.0 8.4
10.9 9.8 11.4 10.6 9.2 9.7 8.3 10.8 9.8 9.0
baseando-se:
10.9 9.8 11.4 10.6 9.2 9.7 8.3 10.8 9.8 9.0
- (a)
- na distribuição assintótica de
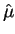
- (b)
- na distribuição limite da função deviance
- (a)
- encontre
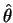
- (b)
- mostre que
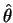 é um estimador não viciado para
é um estimador não viciado para
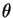 (lembre-se que os valores de
(lembre-se que os valores de 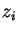 são constantes)
são constantes)
- (c)
- obtenha um intervalo de aproximadamente 95% de confiança
para
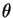 baseado na distribuição assintótica de
baseado na distribuição assintótica de 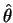
![\includegraphics[width=4in]{exe3.lista2.ps}](img11.png)