Seguinte: Exemplo: Níveis séricos de Acima: Resposta contínua: amostras independentes Anterior: Resposta contínua: amostras independentes
O teste t para duas amostras é adequado para situações em que as respostas aos dois tratamentos são variáveis quantitativas com distribuição gaussiana com parâmetros
![]() e
e
![]() .
.
Suposição do teste: as variáves estudadas têm distribuições gaussianas com o mesmo desvio-padrão.
Note que ![]() ,
, ![]() e
e ![]() são parâmetros populacionais e, portanto constantes desconhecidas.
são parâmetros populacionais e, portanto constantes desconhecidas.
Para testar a hipótese acima,
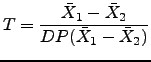
A decisão baseada nesta estatística de teste é intuitiva, pois
Em outras palavras, com a estatística ![]() estamos medindo a diferença entre as médias em termos de desvios-padrão (lembra da interpretação do escore padronizado? É semelhante...).
estamos medindo a diferença entre as médias em termos de desvios-padrão (lembra da interpretação do escore padronizado? É semelhante...).
Devemos rejeitar ![]() se
se ![]() for "grande" em valor absoluto.
for "grande" em valor absoluto.
Para tomarmos esta decisão, usamos a distribuição t de Student (Student, 1908):
Para efetuarmos os cálculos necessários ao teste, precisamos conhecer a expressão para o desvio-padrão de
![]() .
.
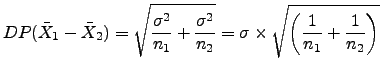
Precisamos encontrar uma estimativa de ![]() para obter uma estimativa do desvio-padrão de
para obter uma estimativa do desvio-padrão de
![]() .
.
Como a suposição é que as variâncias dos dois grupos são iguais, podemos estimar ![]() como uma média ponderada, com pesos proporcionais aos tamanhos dos grupos,
como uma média ponderada, com pesos proporcionais aos tamanhos dos grupos,
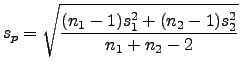
O teste t para comparação de duas amostras consiste em se rejeitar ![]() em favor de
em favor de ![]() ao nível de
ao nível de ![]() de significância, se
de significância, se
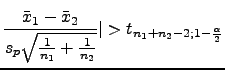
em que
![]() é o percentil de ordem
é o percentil de ordem
![]() da distribuição t com
da distribuição t com ![]() graus de liberdade.
graus de liberdade.
Alternativamente, pode-se obter o valor-p da estatística de teste resultante dos dados e tomar a decisão com base neste p-valor.
silvia 2012-09-20