Seguinte: Exemplo: Eficácia do AZT Acima: Resposta dicotômica: amostras independentes Anterior: Resposta dicotômica: amostras independentes
A Tabela 33 apresenta dados genéricos de uma situação envolvendo a comparação de dois grupos e que a resposta de interesse é dicotômica: a ocorrência ou não de um evento.
| ||||||||||||||||||||
Se não há diferença entre as proporções de ocorrência do evento nos dois grupos, então
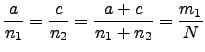
A partir dessas igualdades podemos escrever
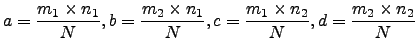
Temos, portanto, dois conjunto de valores: os observados ![]() e os
esperados
e os
esperados ![]() calculados sob a hipótese de igualdade das proporções
de sucesso entre os grupos.
calculados sob a hipótese de igualdade das proporções
de sucesso entre os grupos.
Se as proporções de sobrevivência são iguais nos dois grupos, a discrepância entre os dois conjuntos de números acima não deve ser grande.
Pearson propôs medir a discrepância entre os valores observados e esperados das
quatro entradas de uma tabela
![]() através da expressão
através da expressão
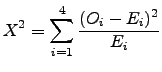
É possível mostrar que o valor do ![]() pode ser calculado de maneira fácil e
algebricamente equivalente através de
pode ser calculado de maneira fácil e
algebricamente equivalente através de
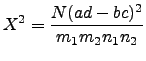
silvia 2012-09-20