Regressão múltipla

Algumas vezes pode ser útil incluir mais do que uma variável independente na equação.

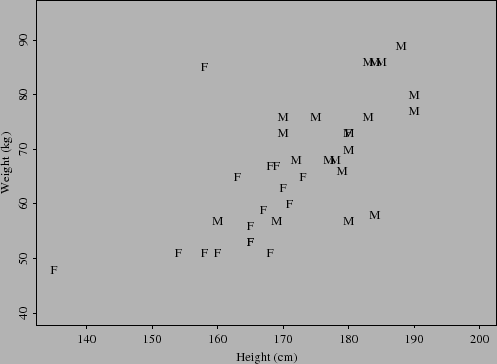
Por exemplo, para predizer o peso de uma pessoa, também seria interessante poder levar em consideração outras informações relevantes disponíveis, tal como o sexo.

Seja sexo$=1$ se a pessoa for do sexo masculino, e 0 se for do sexo feminino.

Ao invés do modelo:

   peso$$= \alpha + \beta \times$$   altura$$,$$

pode ser melhor usar:

   peso$$= \alpha + \beta \times$$   altura$$+ \gamma \times$$   sexo$$.$$

Outras variáveis, tal como idade se disponível, poderia ser incluída no modelo de uma forma similar.

Infelizmente, para mais do que uma variável explanatória, em geral é mais difícil de apresentar os dados em gráficos o que faz com que seja mais difícil avaliar a qualidade de ajuste do modelo.

Para os nossos dados, o modelo é:

   peso$$= -32.79 + 0.56 \times$$   altura$$+ 4.11 \times$$   sexo$$.$$

A reta de regressão nos diz que, ara pessoas da mesma altura, homens tendem a pesar cerca de 4,11 kg a mais do que mulheres.

Além disso, ara pessoas do mesmo sexo, o efeito de altura no peso é cerca de 0,56 kg/cm.

Então para duas pessoas do mesmo sexo, se uma é 10 cm mais alta do que a outra, espera-se que a maior pese cerca de 5,6 kg mais do que a outra.