CE-223: Estatística Computacional

3a Prova, 22 de Julho de 2007

  1. (3,0 pontos) Seja X uma v.a. com distribuição Binomial com n = 15 e p = 0,4, Mostrar os comandos do R para calcular as probabilidades a seguir.
    1. P[X ≥ 14]
    2. P[8 < X ≤ 10]
    3. P[X < 2 ou X ≥ 11]
    4. P[X > 3 e X < 6]
    5. P[X ≤ 13 ∣ X ≥ 11]
    6. P[∣X - 5∣≥ 2]

    Resposta:


    1.   > pbinom(13, size = 15, prob = 0.4, lower = F)

        [1] 2.523293e-05

    2.   > diff(pbinom(c(8, 10), size = 15, prob = 0.4))

        [1] 0.08569975

    3.   > pbinom(1, size = 15, prob = 0.4) + pbinom(10, size = 15, prob = 0.4, lower = F)

        [1] 0.01451970

    4.   > diff(pbinom(c(3, 5), size = 15, prob = 0.4))

        [1] 0.3127136

    5.   > diff(pbinom(c(10, 13), size = 15, prob = 0.4))/pbinom(10, 15, 0.4, lower = F)

        [1] 0.9973006
    6. P[∣X - 5∣≥ 2] = P[X ≤ 3] + P[X ≥ 7]

        > pbinom(3, size = 15, prob = 0.4) + pbinom(6, size = 15, prob = 0.4, lower = F)

        [1] 0.4806887
  2. (2,0 pontos) Seja X uma v.a. com distribuição Normal com μ = 100 e σ2 = 64, Mostrar os comandos do R para calcular as probabilidades a seguir.
    1. P[X > 110]
    2. P[85 < X ≤ 105]
    3. P[X ≤ 95 ou X > 108]
    4. P[∣X - 100∣ < 10]

    Resposta:


    1.   > pnorm(110, mean = 100, sd = 8, lower = FALSE)

        [1] 0.1056498

    2.   > diff(pnorm(c(85, 105), mean = 100, sd = 8))

        [1] 0.7036181

    3.   > pnorm(95, mean = 100, sd = 8) + pnorm(108, mean = 100, sd = 8, lower = FALSE)

        [1] 0.4246408

    4.   > diff(pnorm(c(90, 110), mean = 100, sd = 8))

        [1] 0.7887005
  3. (2,5 pontos) A tabela a seguir mostra a distribuição de frequências das respostas alérgicas (leve, moderada ou forte) de pacientes do sexo feminino e masculino que receberam dosagens altas ou baixas de um certo medicamento.

    reação
    Feminino
    Masculino
    alérgica Dosagem BaixaDosagem AltaDosagem BaixaDosagem Alta
    Leve 21 15 22 34
    Moderada 49 12 14 29
    Forte 28 35 17 11

    As dados foram digitados no R com o seguinte comando:


      > dat <- c(21, 15, 49, 12, 28, 35, 22, 34, 14, 29, 17, 11)
      > ar <- array(dat, dim = c(2, 3, 2))

    Responda as seguintes perguntas e nos ítens onde são mostrados comandos do R explique com palavras o que está sendo calculado e forneça a resposta.

    1. quais as variáveis e quais os níveis das variáveis envolvidas no problema?
    2. qual variável está associada a cada uma das dimensões do array?
    3. apply(ar,2,sum)
    4. apply(ar,3,sum)/sum(ar)
    5. apply(ar, c(3,2), sum)/apply(ar,3,sum)

    Resposta:


      > dimnames(ar) <- list(c("Baixa", "Alta"), c("Leve", "Moderada", "Forte"), c("Feminino",
      +     "Masculino"))
      > apply(ar, 2, sum)

          Leve Moderada    Forte
            92      104       91

      > apply(ar, 3, sum)/sum(ar)

       Feminino Masculino
      0.5574913 0.4425087

      > apply(ar, c(3, 2), sum)/apply(ar, 3, sum)

                     Leve  Moderada     Forte
      Feminino  0.2250000 0.3812500 0.3937500
      Masculino 0.4409449 0.3385827 0.2204724

    1. Variável reaçâo: níveis: leve, moderada, forte
      Variável dosagem: níveis: baixa, alta
      Variável sexo: níveis: feminino, masculino
    2. dimensão 1: variável dosagem, dimensão 2: variável reação, dimensão 3: variável sexo.
    3. totais de indivíduos com cada tipo de reação alérgica
    4. proporções de pessoas de cada sexo dentre todos os pacientes
    5. proporções de cada reação alérgica dentro de cada um dos sexos
  4. (2,5 pontos) Deseja-se fazer um exercício para verificar o algorítmo de geração de números aleatórios do R. Para isto vamos utilizar o teste do dado que consiste em simular uma série de lançamentos de um dado e verificar se os possíveis resultados ocorrem com aproximadamente a mesma frequência. Em outra palavras, precisamos simular lançamentos onde os resultados possíveis 1,2,3,4,5 e 6 ocorrem com a mesma frequência. 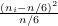Numa segunda etapa, ainda no mesmo contexto, queremos calcular a estatística T = ∑ i=16 2 (ni-nn∕∕66)-- que sabe-se ter distribuição assintótica Chi-Quadrado com 5 graus de liberdade. Mostre como obter o valor para testar ao nível de α = 0.05 a hipótese de que todos os números ocorrem com a mesma frequência. Finalmente, numa terceira fase, deseja-se ilustrar computacionalmente o fato da estatística ter esta distribuição assintótica. Mostre como isto poderia ser feito, incluindo comandos para visualização gráfica dos resultados. Nas três fases deste problema explique com palavras os passos de cada procedimento e mostre o código R necessário para implementar estes passos.
    1. vamos adotar (arbitrariamente) N = 10000 lançamentos e verificar se as frequências observadas são semelhantes

        > dado <- sample(1:6, 10000, rep = T)
        > prop.table(table(dado))

        dado
             1      2      3      4      5      6
        0.1642 0.1704 0.1691 0.1630 0.1696 0.1637

        > 1/6

        [1] 0.1666667
    2. Calcula-se a estatística e o valor crítico de acordo com a distribuição χ2. Alternativamente poderia-se usar a função chisq.text().

        > tab <- table(dado)
        > T <- sum(((tab - (10000/6))^2)/(10000/6))
        > T

        [1] 3.4076

        > pchisq(T, df = 5, lower = F)

        [1] 0.6374127

        > chisq.test(tab, p = rep(1/6, 6))

         Chi-squared test for given probabilities
        
        data:  tab
        X-squared = 3.4076, df = 5, p-value = 0.6374
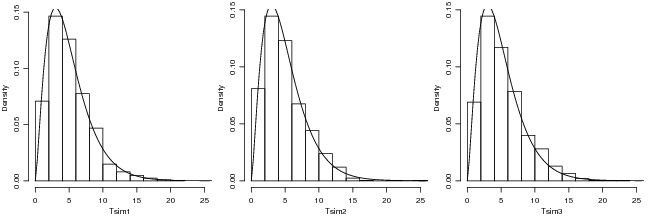
    3. Agora vamos fazer 1000 amostras para o lancamento da moeda 100, 1000 e 10000 vezes e comparar a distribuição da estatística obtida poir simulação com a distribuição χ2.

        > Tfc <- function(tab, size) sum(((tab - (size/6))^2)/(size/6))
        > sim1 <- sapply(1:1000, function(...) {
        +     table(sample(1:6, 100, rep = T))
        + })
        > Tsim1 <- apply(sim1, 2, Tfc, size = 100)
        > sim2 <- sapply(1:1000, function(...) {
        +     table(sample(1:6, 1000, rep = T))
        + })
        > Tsim2 <- apply(sim2, 2, Tfc, size = 1000)
        > sim3 <- sapply(1:1000, function(...) {
        +     table(sample(1:6, 10000, rep = T))
        + })
        > Tsim3 <- apply(sim3, 2, Tfc, size = 10000)

        > fc <- function(x) dchisq(x, df = 5)
        > hist(Tsim1, main = "", prob = T, xlim = c(0, 25))
        > curve(fc, 0, 30, add = T)
        > hist(Tsim2, main = "", prob = T, xlim = c(0, 25))
        > curve(fc, 0, 30, add = T)
        > hist(Tsim3, main = "", prob = T, xlim = c(0, 25))
        > curve(fc, 0, 30, add = T)

      pict