

Nesta seção nos concentramos em alguns testes de hipóteses não paramétricos quando somente uma amostra de observações está disponível. O problema do ajuste é testar a hipótese de que a amostra de observações \(X_1,X_2,\cdots,X_n\) é de alguma distribuição especificada contra a alternativa que é de alguma outra distribuição. Assim, a hipótese nula \(H_0: X\sim F_0\) simples é testada contra a alternativa composta \(H_1: X\sim F\), onde \(F(x)\neq F_0(x)\) para algum \(x\).
Um problema importante na estatística diz respeito à obtenção de informações sobre a forma da população da qual uma amostra é retirada. A forma dessa distribuição pode ser o foco da investigação. Alternativamente, algumas inferências sobre um aspecto particular da população podem ser de interesse. Neste último caso, na estatística clássica, as informações sobre a forma geralmente devem ser postuladas ou incorporadas na hipótese nula para realizar um tipo de inferência paramétrico exato.
Por exemplo, suponha que tenhamos um pequeno número de observações de uma população desconhecida com variância desconhecida e a hipótese de interesse diz respeito ao valor da média populacional. O teste paramétrico tradicional, baseado na distribuição t-Student, é derivado da assertividade de uma população normal. A teoria da distribuição exata e as probabilidades de ambos os tipos de erros dependem dessa população. Portanto, pode ser desejável verificar a razoabilidade da suposição de normalidade antes de formar quaisquer conclusões baseadas na distribuição t-Student. Se a suposição de normalidade parece não ser justificada, algum tipo de inferência não paramétrica para a localização pode ser mais apropriada com um pequeno tamanho de amostra.
Aqui vamos considerar dois tipos de testes de bondade de ajuste. O primeiro tipo é projetado para hipóteses nulas relativas a uma distribuição discreta e compara as frequências observadas com as freqüências esperadas sob a hipótese nula. Este é o teste qui-quadrado proposto por Karl Pearson no início da história da estatística. O segundo tipo de teste de bondade de ajuste é projetado para hipóteses nulas relativas a uma distribuição contínua e compara as freqüências relativas acumuladas observadas com aquelas esperadas sob as hipóteses nulas. Este grupo inclui os testes de Kolmogorov-Smirnov e Lilliefors. Este último éprojetado para testar a suposição de uma distribuição normal ou exponencial com parâmetros não especificados e, portanto, á um teste preliminar importante para justificar o uso de métodos estatísticos paramétricos ou clássicos que exigem essa suposição. Finalmente, apresentamos alguns gráficos para avaliar a forma de uma distribuição.
Uma única amostra aleatória de tamanho \(n\) é extraída de uma população com função de distribuição desconhecida \(F\). Desejamos testar a hipótese nula \begin{equation} H_0: F(x) = F_0(x), \qquad \mbox{para todo } x, \end{equation} onde \(F_0(x)\) é complemanete especificada, contra a alternativa geral \begin{equation} H_0: F(x) \neq F_0(x), \qquad \mbox{para algum } x\cdot \end{equation}
Para aplicar o teste qui-quadrado nesta situação, os dados amostrais primeiro serão agrupados de acordo com algum esquema para formar uma distribuição de frequência. No caso de dados de contagem ou qualitativos, onde a distribuição hipotética seria discreta, as categorias seriam as classificações literais ou numéricas relevantes. Por exemplo, ao jogar os dados as categorias seriam o número de pontos; ao jogar uma moeda, as categorias seriam o número de caras; em pesquisas de preferências de marca, as categorias seriam as marcas consideradas. Quando as observações da amostra são quantitativas, as categorias seriam classes numéricas escolhidas pelo experimentador. Neste caso, a distribuição de frequência não é única e algumas informações são necessariamente perdidas. Embora a distribuição hipotética seja provavelmente contínua com os dados de medição, os dados devem ser categorizados para análise pelo teste qui-quadrado.
Quando a distribuição da população é completamente especificada pela hipótese nula, pode-se calcular as probabilidades de que uma observação aleatória seja classificada em cada uma das categorias escolhidas ou fixas. Essas probabilidades multiplicadas por \(n\) fornecem as frequências para cada categoria que seriam esperadas se a hipótese nula fosse verdadeira. Excetuando-se a variação amostral, deve haver uma concordância próxima entre essas frequências esperadas e observadas se os dados da amostra forem compatíveis com a distribuição \(F_0\) especificada. As frequências observadas e esperadas correspondentes podem ser comparadas visualmente usando um histograma, um polígono de frequência ou um gráfico de barras. O teste qui-quadrado de bondade de ajuste fornece uma base probabilística para efetuar a comparação e decidir se a falta de concordância é muito grande para ter acurado por acaso.
Suponha que as \(n\) observações foram agrupadas em \(k\) categorias mutuamente exclusivas e denote as frequências observadas e esperadas para a \(i\)-ésima classe como \(f_i\) e \(e_i\), respectivamente, \(i=1,2,\cdots,k\). A decisão sobre o ajuste deve se r baseada nos desvios \(f_i-e_i\). A soma desses \(k\) desvios é zero, exceto para arredondamentos. O critério de teste sugerido por Karl Pearson em 1900 é a soma dos quadrados desses desvios, normalizados pela frequência esperada, ou seja \begin{equation} Q=\sum_{i=1}^k \dfrac{(f_i-e_i)^2}{e_i}\cdot \end{equation}
Um grande valor de \(Q\) refletiria uma incompatibilidade entre as frequências relativas observadas e esperadas, portanto, a hipótese nula usada para calcular o \(e\) deve ser rejeitada para \(Q\) grande. A distribuição exata da variável aleatória \(Q\) é bastante complicada, mas para amostras grandes sua distribuição é aproximadamente qui-quadrado com \(k-1\) graus de liberdade. A base teórica para isso pode ser discutida brevemente como segue.
As únicas variáveis aleatórias de interesse são as frequéncias de classe \(F_1,F_2,\cdots,F_k\), que constituem um conjunto de variáveis aleatórias da distribuição mutinomial de dimensão \(k\) com \(k\) resultados possíveis, sendo o resultado desta \(i\)-ésima categoria no sistema de classificação. Com \(\theta_1,\theta_2,\cdots,\theta_k\) indicando as probabilidades dos respectivos resultados e \(f_1,f_2,\cdots,f_k\) denotando os resultados observados, a função de verossimilhança da amostra é então \begin{equation} L(\theta_1,\theta_2,\cdots,\theta_k) \, = \, \prod_{i=1}^k \theta_i^{f_i}, \qquad f_i=0,1,2,\cdots,n, \end{equation} satisfazendo que \(\displaystyle \sum_{i=1}^k f_i=n\), \(\displaystyle \sum_{i=1}^k \theta_i=1\).
A hipótese nula foi assumida para especificar a distribuição da população completamente, a partir do qual o \(\theta_i\) pode ser calculado. Esta hipótese, então, está preocupada apenas com os valores desses parâmetros e pode ser escrita como \begin{equation} H_0: \theta_i^0 \, = \, \dfrac{e}{n}, \qquad i=1,2,\cdots,n\cdot \end{equation}
É fácil mostrar que as estimativas de máxima verossimilhança dos parâmetros são \(\widehat{\theta}_i=f_i/n\). A estatística da razão de verossimilhança para esta hipótese é então \begin{equation} \mathcal{L}=\dfrac{L(\theta_1^0,\cdots,\theta_k^0)}{L(\widehat{\theta}_1,\cdots,\widehat{\theta}_k)} \, = \, \displaystyle \prod_{i=1}^k \left(\dfrac{\theta_i^0}{\widehat{\theta}_i}\right)^{f_i}\cdot \end{equation} Como dissemos, a distribuição da variável aleatória \(-2n\mathcal{L}\) pode ser aproximada pela distribuição qui-quadrado. Os graus de liberdade são \(k-1\), uma vez que a restrição \(\sum_{i=1}^k \theta_i = 1\) deixa apenas \(k-1\) parâmetros no espaço paramétrico para serem estimados independentemente. Nós temos aqui \begin{equation} -2\ln\mathcal{L} \, = \, -2\sum_{i=1}^k f_i\left( \ln(\theta_i^0)-\ln(f_i/n)\right)\cdot \end{equation}
Vamos agora mostrar que a expressão acima é assintoticamente equivalente à expressão para \(Q\). A expansão em série de Taylor de \(\ln(\theta_i)\) a respeito de \(f_i/n=\widehat{\theta}_i\) é \begin{equation} \ln(\theta_i) \, = \, \ln(\widehat{\theta}_i)+(\theta_i-\widehat{\theta}_i)\frac{1}{\widehat{\theta}_i} -\frac{(\theta_i-\widehat{\theta}_i)^2}{2!}\frac{1}{\widehat{\theta}_i^2}+\epsilon_i, \end{equation} de maneira que \begin{equation} \ln(\theta_i^0) -\ln(f_i/n) \, = \, \Big( \theta_i^0-\frac{f_i}{n}\Big)\frac{n}{f_i}- \Big( \theta_i^0-\frac{f_i}{n}\Big)^2\frac{n^2}{2f_i^2}+\epsilon \, = \, \dfrac{(n\theta_i^0-f_i)}{f_i}- \dfrac{(n\theta_i^0-f_i)^2}{2f_i^2}+\epsilon_i, \end{equation} onde \(\displaystyle \epsilon_i=\sum_{j=3}^\infty (-1)^{j+1}\Big( \theta_i^0-\frac{f_i}{n}\Big)^j\frac{n^j}{j!f_i^j}\).
Substituindo apropriadamesnte temos que \begin{equation} -2\ln\mathcal{L} \, = \, -2\sum_{i=1}^k \big( \theta_i^0-f_i\big)+\sum_{i=1}^k \frac{\big( \theta_i^0-f_i\big)^2}{f_i} + \sum_{i=1}^k \epsilon_i \, = \, \sum_{i=1}^k \frac{\big( f_i-e_i\big)^2}{f_i} +\epsilon\cdot \end{equation} Pela Lei dos Grandes Números \(F_i/n\) é conhecido ser um estimador consistente de \(\theta_i\) ou \begin{equation} \lim_{n\to\infty} \frac{1}{n}P\big(|F_i-n\theta_i|>\epsilon\big) \, = \, 0, \qquad \mbox{para todo } \epsilon>0\cdot \end{equation}
Assim, vemos que a distribuição de probabilidade de \(Q\) converge para a de \(-2\ln\mathcal{L}\), que é qui-quadrado com \(k-1\) grau de liberdade. Esta aproximação pode ser usada com confiança, desde que cada frequência esperada seja pelo menos igual a 5. Para qualquer \(e_i\) menor que 5, o procedimento usual é combinar grupos adjacentes na distribuição de frequência até que essa restrição seja satisfeita. O número de graus de liberdade, em seguida, deve ser reduzido para corresponder ao número real de categorias usadas na análise. Esta regra de 5 não deve ser considerada inflexível, no entanto. É conservador, e a aproximação qui-quadrado é razoavelmente precisa para frequências celulares esperadas tão pequenas quanto 1.5.
Qualquer caso em que os \(\theta_i\) são completamente especificados pela hipótese nula é, portanto, facilmente manipulado. A situação mais típica, no entanto, é quando a hipótese nula é composta, isto é, declaramos a forma da distribuição, mas não todos os parâmetros. Por exemplo, quando testamos se uma amostra é retirada de alguma população normal, \(\mu\) e \(\sigma\) não seriam dados. No entanto, para calcular as frequências esperadas em \(H_0\), \(\mu\) e \(\sigma\) devem ser conhecidas. Se as frequências esperadas são estimadas a partir dos dados como \(n\widehat{\theta}_1^0\), a variável aleatória para o teste de ajuste assume a forma \begin{equation} Q=\sum_{i=1}^k \dfrac{\big( F_i-n\widehat{\theta}_i^0\big)^2}{n\widehat{\theta}_i^0}\cdot \end{equation}
A distribuição assintótica de \(Q\) pode então depender do método empregado para a estimação. Quando os estimadores são encontradas pelo método de máxima verossimilhança para os dados agrupados, o numerador na estatística do teste de razão de verossimilhança é \(L(\widehat{\theta}_1^0,\widehat{\theta}_2^0,\cdots,\widehat{\theta}_k^0)\), onde os \(\widehat{\theta}_i^0\) são os estimadores de máxima verossimilhança de \(\theta_i^0\) em \(H_0\). A derivação da distribuição de \(\mathcal{L}\) e, portanto, \(Q\) mantém-se exatamente como antes, exceto para os graus de liberdade. Os graus de liberdade para \(Q\) são então \(k-1-s\), onde \(s\) é o número de parâmetros independentes em \(F_0\) foram estimados a partir dos dados agrupados para estimar todos os \(\theta_i^0\).
No teste de bondade de ajuste normal, por exemplo, as estimativas dos parâmetros \(\mu\) e \(\sigma\) seriam calculadas a partir dos dados agrupados e usadas com quantiles da distribuição normal para encontrar \(n\widehat{\theta}_i^0\) e os graus de liberdade para \(k\) categorias iria para \(k-3\). Quando os dados originais são desagrupados e os estimadores de máxima verossimilhança são baseados na função de verossimilhança de todas as observações, a teoria é diferente. Chernoff and Lehmann (1954) mostraram que a distribuição limite de \(Q\) não é qui-quadrado neste caso e que \(P(Q> \chi^2_\alpha)> \alpha\). O teste é então anticonservador. A investigação deles mostrou que o erro é consideravelmente mais sério para a distribuição normal do que para a Poisson. Um ajuste possível é discutido em seu artigo. Na prática, no entanto, a estatística acima é frequentemente tratada como uma variável qui-quadrado de qualquer maneira.
| Números de defeitos | Número de amostras | |
|---|---|---|
| 0 | 10 | |
| 1 | 24 | |
| 2 | 10 | |
| 3 | 4 | |
| 4 | 1 | |
| 5 | 1 | |
| 6 ou mais | 0 | |
Como os dados são agrupados e ambas as distribuiçães nulas hipotéticas são discretas, o teste de bondade qui-quadrado é apropriado. Como nenhum parâmetro é especificado, eles devem ser estimados a partir dos dados para realizar o teste.
Neste teste procedemos da seguinte maneira: estimamos a função de distribuição empírica da amostra e calculamos uma estatística cujo valor mede o afastamento da função de distribuição empírica da amostra daquela da distribuição nula.
Observemos na figura abaixo que o objetivo desta estatística é encontrar a diferença máxima entre a distribuição suposta dos dados \(F\) e a distribuição empírica \(\widehat{F}_n\). Nesta figura apresentamos dois exemplos: à esquerda simulamos 50 dados normais e mostramos a função de distribuição normal padrão acumulada, curva em vermelho, assim como a correspondente distribuição empírica; à direita simulamos uma distribuição diferente.
 |
 |
|---|
Na figura acima à direita mostramos à função de distribuição empírica correspondente à amostra obtida da distribuição Gama(3,1) enquantro a curva vermelha corresponde à distriuição teórica respectiva.
Sem perda de generalidade, portanto, assumimos que \(F\) seja a função de distribuição de uma variável aleatória \(U(0,1)\).
Seja \(D_{n,\alpha}\) o ponto \(\alpha\)-percentual superior da distribuição de \(D_n\), isto é, \(P\big(D_n>D_{n,\alpha}\big)\leq \alpha\). A distribuição exata de \(D_n\) para valores selecionados de \(n\) e \(\alpha\) foi tabulada por Miller (1956), Owen (1962) e Birnbaum (1952). A distribuição \(D_n\) em amostras grandes foi derivada por Kolmogorov e a apresentamos a seguir.
Este teorema pode ser usado para encontrar \(d_n\) tal que \(\lim_{n\to\infty} P\big(\sqrt{n}D_n\leq d_n\big)=1-\alpha\). Tabelas de \(d_n\) para vários valores de \(\alpha\) foram disponibilizados por Owen (1962). As estatísticas \(D_n^+\) e \(D_n^-\) têm a mesma distribuição devido à simetria e sua distribuição comum é dada no seguinte teorema.
Tabelas para os valores criticos \(D_{n,\alpha}^+\), onde \(P\big( D_n^+>D_{n,\alpha}^+ \big)\leq \alpha\), foram disponibilizados para valores selecionados de \(n\) e \(\alpha\) em Birnbaum & Tingey (1951). No caso de amostras grandes Smirnov (1944) demonstrou que \begin{equation} \lim_{n\to\infty} P\big(\sqrt{n}D_n^+\leq z\big)=1-e^{-2z^2}, \quad z\geq 0\cdot \end{equation} De fato, em vista da expressão acima, a estatística \(V_n=4n{D_n^+}^2\) tem distribuição limite \(\chi^2(2)\), para \(4n{D_n^+}^2\leq 4z^2\) se e somente se \(\sqrt{n}D_n^+\leq z\), \(z\geq 0\), e o resultado segue desde que \begin{equation} \lim_{n\to\infty} P\big(V_n\leq 4z^2\big)=1-e^{-2z^2}, \quad z\geq 0, \end{equation} de modo que \begin{equation} \lim_{n\to\infty} P\big(V_n\leq x\big)=1-e^{-x/2}, \quad x\geq 0\cdot \end{equation} a qual é a função de distribuição de uma variável aleatória \(\chi^2(2)\). Todos estes resultados estão programados na função R ks.test, esta função fornece-nos tanto o valor do estatística \(D_n\) quanto o p-valor, seja este encontrado de maneira exata ou através da distribuição limite.
Vejamos uma situação diferente na qual rejeitamos primeiro a hipótese nula de a amostra seja N(0,1), mas verificando detalhadamente a amostra podemos encontrar uma distribuição adequada.
 |
 |
|---|
Vale a pena comparar o teste qui-quadrado de bondade de ajuste e o teste de Kolmogorov-Smirnov. O segundo trata diretamente das observações individuais enquanto o primeiro discretiza os dados e, às vezes, perde informações por meio do agrupamento. Além disso, o teste de Kolmogorov-Smirnov é aplicável mesmo no caso de amostras muito pequenas, mas o teste do qui-quadrado é essencialmente para amostras grandes.
O teste qui-quadrado, por outro lado, pode ser facilmente modificado para permitir a estimação de parâmetros a partir dos dados, mas o teste de Kolmogorov-Smirnov não tem essa flexibilidade. O teste qui-quadrado pode ser aplicado quando os dados são discretos ou contínuos, mas o teste de Kolmogorov-Smirnov pressupõe a continuidade da função de distribuição. Isso significa que o último teste fornece uma análise mais refinada dos dados. Se a distribuição é realmente descontínua, o teste de Kolmogorov-Smirnov é conservador na medida em que tende a aceitar \(H_0\).
Voltamos nossa atenção para alguns outros usos da estatística Kolmogorov-Smirnov. Seja \(X_1,X_2,\cdots,X_n\) uma amostra aleatória da função de distribuição \(F\) e seja \(\widehat{F}_n\) a função de distribuição empírica. A estimativa \(\widehat{F}_n\) de \(F\), para \(n\) grande, deve ser pró,xima a \(F\). De fato, \begin{equation} P\Big( |\widehat{F}_n(x)-F(x)|\leq \frac{\epsilon\sqrt{F(x)[1-F(x)]}}{\sqrt{n}}\Big)\geq 1-\dfrac{1}{\epsilon^2} \end{equation} e, desde que \(F(x)[1-F(x)]\leq \frac{1}{4}\), temos que \begin{equation} P\Big( |\widehat{F}_n(x)-F(x)|\leq \frac{\epsilon}{2\sqrt{n}}\Big)\geq 1-\dfrac{1}{\epsilon^2}\cdot \end{equation} Assim \(\widehat{F}_n\) pode ser escolhido próximo a \(F\) com alta probabilidade escolhendo \(\epsilon\) e um \(n\) suficientemente grande. A estatística de Kolmogorov-Smirnov nos permite determinar o menor \(n\) tal que o erro na estimativa nunca exceder um valor fixo \(\delta\) com uma grande probabilidade \(1- \alpha\). Desde que \begin{equation} P\Big(D_n\leq \delta\Big)\geq 1-\alpha, \end{equation} \(\delta=D_{n,\alpha}\) e, dado \(\delta\) e \(\alpha\), podemos ler \(n\) das tabelas das probabilidades acima. Para \(n\) grande, podemos usar a distribuição assintótica de \(D_n\) e resolver \(d_{\alpha}=\delta\sqrt{n}\) para \(n\).
Nós também podemos formar limites de confiança para \(F\). Dado \(\alpha\) e \(n\), primeiro encontramos \(D_{n,\alpha}\) de forma que \begin{equation} P(D_n>D_{n,\alpha})\leq \alpha, \end{equation} o qual é o mesmo que \begin{equation} P\Big( \sup_x |\widehat{F}_n(x)-F(x)|\leq D_{n,\alpha}\Big)\geq 1-\alpha\cdot \end{equation} Portanto \begin{equation} P\Big( |\widehat{F}_n(x)-F(x)|\leq D_{n,\alpha} \quad para \; todo \; x\Big)\geq 1-\alpha\cdot \end{equation} Definamos \begin{equation} L_n(x)=\max\Big( \widehat{F}_n(x)-D_{n,\alpha},0 \Big) \quad e \quad U_n(x)=\min\Big( \widehat{F}_n(x)+D_{n,\alpha},1 \Big)\cdot \end{equation} Então, a região entre \(L_n(x)\) e \(U_n(x)\) pode ser usada como uma banda de confiança para \(F(x)\) com o coeficiente de confiança associado \(1-\alpha\).
Em relação à distribuição de \(D_n\), utilizaremos um novo algoritmo para calcular probabilidades \(D_n < D_{n,\alpha}\) proposto por Carvalho (2015). Este algoritmo é uma versão melhorada do método originalmente proposto por Wang, Tsang e Marsaglia (2003) baseado no resultado de Durbin (1973). O novo algoritmo mantém a mesma precisão numérica do Wang et al. (2003), mas é mais eficiente. O método proposto é implementado no pacote R kolmim.
 |
|---|
O teste de normalidade de Lilliefors é uma adaptação do teste Kolmogorov-Smirnov para o caso em que a média e a variância da distribuição normal são desconhecidos. Seja \(X_1,X_2,\cdots,X_n\) uma amostra aleatória de tamanho \(n\). Estimamos a média e a variância dos dados usando os estimadores não viciados \begin{equation} \widehat{\mu}=\overline{X} \qquad \mbox{e} \qquad \widehat{\sigma}^2=s^2=\frac{1}{n-1}\sum_{i=1}^n (X_i-\overline{X})^2\cdot \end{equation}
Aqui nós consideramos o problema do teste de bondade do ajuste para a distribuição normal sem média e variância especificadas. Este problema é muito importante na prática, porque a suposição de uma distribuição normal com \(\mu\) e \(\sigma\) é necessária para tantos testes estatísticos clássicos e procedimentos de estimação. Nesse caso, observe que a hipótese nula é composta porque afirma que a distribuição subjacente é alguma distribuição normal. Em geral, o teste Kolmogorv-Smirnov pode ser aplicado no caso de hipóteses compostas de ajuste de qualidade após estimar os parâmetros desconhecidos, \(F_0\) será então substituído por \(\widehat{F}_0\).
infelizmente, a distribuição nula da estatística de teste Kolmogorov-Smirnov com parâmetros estimados é muito mais complicada. Isso, obviamente, afeta os cálculos do p-valor. Para a distribuição normal, Lilliefors (1967) mostrou que a utilização dos pontos críticos usuais desenvolvidos para o teste Kolmogorov-Smirnov fornece resultados extremamente conservadores. Ele então usou simulações Monte Carlo para desenvolver uma tabela para a estatística Kolmogorov-Smirnov que fornece valores críticos precisos. Como antes, a estatística Kolmogorov-Smirnov é definida como \begin{equation} D_n=\sup_{x} |\widehat{F}_n(x)-\widehat{F}_0(x)|, \end{equation} onde \(\widehat{F}_n\) é a função de distribuição empírica e \(\widehat{F}_0\) é calculado como a distribuição normal padrão \(\Phi(z)\) onde \(z=(x-\widehat{x})/s\) para cada observação \(x\), \(\widehat{x}\) a média amostral das \(n\) observações e \(s^2\) o estimador não viciado de \(\sigma^2\), calculado com \(n-1\) no denominador. A hipótese nula de normalidade é rejeitada se \(D_n> c\), onde \(c\) é o valor de corte. Os valores de corte desta estatística de teste para valores selecionados de \(n\) e diferentes níveis de significância podem ser encontrados em Dallal e Wilkinson (1986) sendo apenas confiáveis quando o p-valor é menor que 0.100. Uma aproximação analítica, devida a estes mesmos autores, da probabilidade de cauda superior \(p\), da distribuição de \(D_n\) para menos de 0.100 e tamanho de amostra \(n\) entre 5 e 100 é dada por \begin{equation} \exp\Big( -7.01256 D_n^2(n+2.789019)+2.99587 D_n\sqrt{n+2.78019}-0.122119+\frac{0.974598}{\sqrt{n}}+\frac{1.67997}{n}\Big)\cdot \end{equation} Para amostras de tamanho \(n>100\), a mesma expressão é utilizada com \(D_n\) substituído por \(D_n\times \big(\frac{n}{100}\big)^{0.49}\). Se o p-valor de Dallal-Wilkinson for superior a 0.100, então o p-valor é calculado a partir da distribuição da estatística modificada \(D_n\big(\sqrt{n}-0.01+0.85/\sqrt{n}\big)\), ver Stephens (1974). A fórmula real do p-valor sendo obtida por um processo de simulação e aproximação disponível na função lillie.test no pacote nortest.
A estatística do teste de Cramér-von Mises pertence ao grupo de estatísticas de bondade do ajuste baseadas em uma comparação da função de distribuição empírica de uma dada amostra com a distribuição teórica a ser testada. Ela é projetada para testar que a variável aleatária \(X\) tem uma distribuição contínua \(F(\cdot;\theta)\); sendo \(\theta\) um vetor de um ou mais parâmetros que entram na função de distribuição. Assim, para a distribuição normal, o vetor \(\theta=(\mu,\sigma^2)\).
Muitas estatísticas deste tipo foram propostas, a mais famosa e uma das mais antigas sendo a \(D_n\) de Kolmogorov-Smirnov. Esta estatística é baseada na maior discrepância vertival entre as duas funções. Uma medida alternativa é a família \begin{equation} W^* = \int_{-\infty}^\infty \big[\widehat{F}_n(x)-F(\cdot;\theta)\big]^2\psi(x)f(x)\mbox{d}x, \end{equation} sendo, \(f\) a função de densidade sob a hipóteses nula e, no caso da estatástica Cramér-von Mises, \(\psi(x)=1\). A expressão computacional da estatástica de teste é \begin{equation} W_n^*=\frac{1}{n}\sum_{i=1}^n \Big( F_0\big(X_{(i})\big)-\frac{2i-1}{2n}\Big)^2+\frac{1}{12n^2}, \end{equation} onde \(X_{(1)},X_{(2)},\cdots,X_{(n)}\) são as estatásticas de ordem. Considerando certa a hipótese nula \(H_0\), a distribuição limite desta estatástica é bem conhecida e sabe-se que em amostras finitas \(W_n^*\) aborda este limite muito rapidamente.
A expressão de \(W_n^*\) sugere uma maneira de avaliar os valores críticos do teste de Cramér-von Mises por simulações Monte Carlo. Simplesmente geram-se variáveis aleatórias independentes \(\epsilon_1,\cdots,\epsilon_n\) da distribuição \(Uniforme(0,1)\) e calcula-se \(W_n^*\) cada amostra Monte Carlo. Em um grande número de amostras Monte Carlo, o percentil de \(100(1-\alpha)\) dos valores calculados para \(W_n^*\), aproxima-se então dos valores críticos do teste correspondentes no nível de significância \(\alpha\) para qualquer \(\alpha\in (0,1)\) de acordo com a Lei dos Grandes Números.
A estatística do teste de Anderson-Darling pertence ao grupo de estatísticas de bondade do ajuste baseadas em uma comparação da função de distribuição empírica de uma dada amostra com a distribuição teórica a ser testada. Ela é projetada para testar que a variável aleatária \(X\) tem uma distribuição contínua \(F(\cdot;\theta)\); sendo \(\theta\) um vetor de um ou mais parâmetros que entram na função de distribuição. Assim, para a distribuição normal, o vetor \(\theta=(\mu,\sigma^2)\).
Muitas estatísticas deste tipo foram propostas, a mais famosa e uma das mais antigas sendo a \(D_n\) de Kolmogorov-Smirnov. Esta estatística é baseada na maior discrepância vertival entre as duas funções. Uma medida alternativa é a família \begin{equation} W^* = \int_{-\infty}^\infty \big[\widehat{F}_n(x)-F(\cdot;\theta)\big]^2\psi(x)f(x)\mbox{d}x, \end{equation} sendo no caso desta situação \begin{equation} \psi(x)=\frac{1}{F(\cdot;\theta)[1-F(\cdot;\theta)]}\cdot \end{equation} Essa função de peso neutraliza o fato de que a discrepância entre \(\widehat{F}_n\) e \(F\) está necessariamente se tornando menor nas caudas, uma vez que ambas abordam 0 e 1 nos extremos. A função de peso dada pesa a discrepância por um fator inversamente proporcional à sua variância, e tem o efeito de dar grande importância às observações na cauda do que a maioria das outras estatísticas. Esta estatística é recomendada com boas propriedades de poder sobre uma ampla gama de distribuições alternativas quando \(F\) não é a verdadeira distribuição.
Para fins práticos, a definição da estatística Anderson-Darling acima precisa ser transformada em uma fórmula computacional. Dada a amostra \(X_1,X_2,\cdots,X_n\), calculamos \(Z_i=F(X_{(i)};\theta)\), \(i=1,2,\cdots,n\) do qual temos que a estatística de Aderson-Darling assume a forma \begin{equation} A^2 = -\frac{\displaystyle\sum_{i=1}^n (2i-1)\Big(\ln(Z_i)-\ln(1-z_{n+1-i})\Big)}{n}-n\cdot \end{equation}
A fórmula para \(Z_i\) acima assume que a distribuição testada \(F\) é completamente especificada, isto é, os parâmetros em \(\theta\) devem ser conhecidos. A estatística \(A^2\) foi introduzida por Anderson and Darling (1954) e para esta situação eles deram a distribuição assintótica e tabelas de porcentagem de pontos. Para fins de teste, a cauda superior de \(A^2\) será usada; grandes discrepâncias entre a distribuição empírica e a distribuição testada indicarão um ajuste inadequado.
Mais tarde, Lewis (1961) demonstrou que a distribuição de \(A^2\) para uma amostra finita aproxima-se da distribuição assintótica de forma extremamente rápida de modo que, para fins práticos, apenas a distribuição assintótica é necessária para tamanho de amostra maior que 5.
A distribuição de \(A^2\) para o caso de parâmetros conhecidos é a mesma para todas as distribuições testadas. Isso ocorre porque a transformação integral da probabilidade é feita na primeira etapa, quando calculamos \(Z_i=F(X_{(i)};\theta)\) e os valores de \(Z_i\) são valores ordenados de uma distribuição uniforme com os limites 0 e 1. \(A^2\) é, portanto, uma função de variáveis aleatórias uniformes ordenadas. A teoria da distribuição assintótica para este caso especial pode ser encontrada a partir da teoria assintótica da função de distribuição empírica ou, mais especificamente, da função \begin{equation} \sqrt{n}\Big(\widehat{F}_n(z)-z\Big)\cdot \end{equation}
Quando \(\theta\) contém componentes desconhecidos os \(Z_i\), dados pela transformação acima, quando um estimador \(\widehat{\theta}\) substitui \(\theta\), não serão variáveis aleatórias ordenadas com distribuição uniformes e a teoria de distribuição de \(A^2\), torna-se substancialmente mais difícil. Em geral, a distribuição de \(A^2\) depende de \(n\) e também dos valores dos parâmetros desconhecidos.
Felizmente, uma simplificação importante ocorre se os componentes desconhecidos de \(\theta\) forem apenas parâmetros de localização e escala. Então a distribuição desta estatística, com uma estimativa apropriada para \(\theta\), dependerá da distribuição testada, mas não do valor específico dos parâmetros desconhecidos. Assim, para o teste da distribuição normal, por exemplo, com \(\mu\) e \(\sigma^2\) desconhecidos, apenas um conjunto de tabelas seria necessário, de porcentagens para cada \(n\). Esta simplificação faz com que seja possível calcular a teoria assintótica para \(A^2\), e isto foi feito para o caso normal e outros na função AndersonDarlingTest, pacote de funções DescTools.
O Teorema Central do Limite afirma que, sujeito a que o segundo momento é finito, a média amostral \(\overline{X}\) de observações independentes identicamente distribuídas é assintoticamente normal no sentido de que \begin{equation} \frac{\sqrt{n}}{\sigma}\big( \overline{X}-\mu\big) \overset{D}{\longrightarrow} Z, \qquad n\to\infty, \end{equation} onde \(Z\sim N(0,1)\), \(\mu=\mbox{E}(X_1)\) e \(\sigma^2=\mbox{Var}(X_1)\). Ao longo dos anos, esse surpreendente resultado informou ou até mesmo confundiu seus usuários. Por exemplo, ele diz que não importa qual seja a distribuição populacional da amostra, a distribuição limite no lado direito é sempre a mesma: a distribuição normal padrão. Imagine quão diferente a distribuição da população pode ser em termos de sua forma: simétrica, distorcida, bimodal, contínua, discreta e assim por diante. No entanto, elas não fazem diferença enquanto ao teorema do limite central.
No entanto, o teorema central do limite é correto do ponto de vista teórico e isso foi confirmado por inúmeros estudos empíricos. Aqui, do ponto de vista teórico, isso significa que \(n\to\infty\) ou pelo menos é muito grande. No entanto, em uma situação de amostra finita, pode ser uma história diferente. Por exemplo, suponha que \(n=30\). Pode ser mostrado que neste caso a forma da distribuição da população faz diferença. Isso levanta uma questão sobre a taxa de convergência do teorema central do limite. Em particular, duas medidas da forma da distribuição da população são a assimetria e a curtose, definidas como \begin{equation} \kappa_3 \, =\, \frac{\mbox{E}(X_1-\mu)^3}{\sigma^3} \end{equation} e \begin{equation} \kappa_4 \, =\, \frac{\mbox{E}(X_1-\mu)^4}{\sigma^4}-3, \end{equation} respectivamente. Seria de se esperar que essas características tivessem algum impacto na taxa de convergência do teorema central do limite. Por exemplo, o célebre teorema de Berry-Essen, descoberto por Berry (1941) e Essen (1942), afirma que se o terceiro momento de \(X_1\) é limitado, então \begin{equation} \sup_x |F_n(x)-\Phi(x)|\leq \frac{c\mbox{E}(|X_1|^3)}{\sqrt{n}}, \end{equation} onde \(F_n\) é a função de distribuição de \(\xi_n=(\sqrt{n}/\sigma)(\overline{X}-\mu)\), \(\Phi\) a função de distribuição normal padrão e \(c\) uma constante que não de depende da distribuição de \(X_1\). A expansão de Edgeworth, batizada em homenagem ao matemático irlandês Francis Ysidro Edgeworth (1845-1926), é uma forma de aprimorar a desigualdade acima a ordens superiores.
Como a expansão de Taylor, a expansão de Edgeworth pode ser expressa em \(k + 1\) termos mais um resíduo. A diferença é que, na expansão de Taylor, os termos estão em ordens decrescentes de \(|x-a|\) e na exopansão de Edgeworth, os termos estão em ordem decrescente de \(n^{-1/2}\). Por uma questão de simplicidade, focamos principalmente no caso \(k=2\), que pode ser expresso como \begin{equation} F_n(x) \, = \, \Phi(x) \, + \, \frac{\kappa_3p_1(x)}{6\sqrt{n}}\phi(x) \, + \, \frac{\kappa_4p_2(x)-\kappa_3^2p_3(x)}{24n}\phi(x) \, + \, O(n^{-3/2}), \end{equation} onde \(\phi(x)\) é a função de densidade normal padrão, ou seja, \(\phi(x)=(1/\sqrt{2\pi})e^{-x^2/2}\), \begin{equation} p_1(x) \, = \, 1-x^2, \qquad p_2(x) \, = \, x(3-x^2) \qquad \mbox{e} \qquad p_3(x) \, = \, \frac{x}{3}(15-10x^2+ x^4)\cdot \end{equation} Vemos que o primeiro e o segundo termos da expansão de Edgeworth envolvem a assimetria \(\kappa_3\) e a curtose \(\kappa_4\), confirmando nossa especulação anterior de que essas quantidades podem influenciar a taxa de convergência do teorema central do limite. Também podemos perceber que se \(\kappa_3=0\) e \(\kappa_4=0\), então a aproximação à distribuição normal padrão seria quase perfeita.
Na análise univariada de dados, uma das hipóteses mais utilizadas é a suposição de normalidade. Além disso, a normalidade comumente assumida nos ajuda a estimar e fazer comparações e julgamentos inferenciais. No entanto, a violação dessa suposição pode produzir inferências enganosas e o resultado do uso de inferências não confiáveis é produzir interpretações enganosas. Testes de normalidade devem ser tão importantes quanto a suposição de normalidade. O método mais amplamente utilizado, pelo menos na econometria, que foi sugerido e usado para testar se a distribuição subjacente a uma amostra é normal é a estatística de Bowman and Shenton (1975): \begin{equation} JB = n\left( \frac{\kappa_3^2}{6}+\frac{\kappa_4^2}{24} \right), \end{equation} que posteriormente foi derivado por Jarque and Bera (1987). Por esse motivo, a estatástica de teste \(JB\) também chamado de teste de Jarque-Bera.
A estatística \(JB\) tem uma distribuição assintótica chi-quadrada com dois graus de liberdade. Esta estatística é simples e seu poder se mostrou comparável a outros testes poderosos. Está programada na JarqueBeraTest no pacote DescTools.
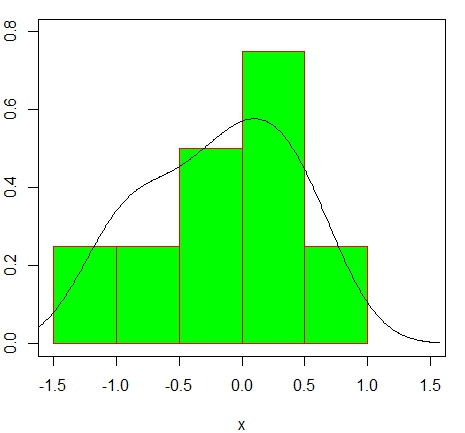
Com o advento da tecnologia de computação facilmente disponível, abordagens visuais para análise de dados estatísticos tornaram-se populares. O assunto é algumas vezes chamado de análise exploratória de dados. No contexto dos testes de qualidade de ajuste, as ferramentas exploratórias de análise de dados empregadas incluem grááficos de pontos, histogramas, gráficos de probabilidade e grááficos de quantiles. A ideia é usar alguns gráficos para obter uma visão rápida da distribuição subjacente e, em seguida, se desejar, realizar uma análise de acompanhamento com um teste confirmatório formal, como qualquer um dos testes abordados anteriormente aqui. Todos estes gráficos de são ferramentas explicativas valiosas discutidas em quase todos os livros de estatística. Observe que existem versões de duas amostras de cada um desses gráficos, mas não abordamos esse tópico agora.
A seguir, distinguimos entre as versões teórica e empírica de um gráfico. A versão teórica é apresentada para entender a ideia, mas a versão empírica é aquela implementada na prática. Dois tipos de gráficos são populares na prática. O primeiro é o chamado gráfico de probabilidade, que é na verdade um gráfico de probabilidade versus probabilidade ou p-p plot. Este gráfico também é chamado de plotagem percentual, por razões óbvias. Em termos gerais, o gráfico p-p plot teórico é o gráfico de uma função de distribuição \(F(x)\) versus uma função de distribuição \(G(x)\) para todos os valores de \(x\). Como as funções de distribuição são probabilidades, o gráfico p-p plot é convenientemente confinado ao quadrado unitário. Se as duas funções de distribuições forem idênticas o gráfico teórico p-p plot será a diagonal principal, a linha de 45 graus através da origem. Este gráfico é amplamente utilizado para avaliar a assimetria de uma distribuição.
 |
 |
|---|
Para concluir percebemos que o gráfico p-p plot compara uma amostra com um modelo teórico e representa a proporção teórica menor ou igual a cada valor observado em relação à proporção real.
O segundo tipo de gráfico é o chamado quantile plot, que é na verdade um gráfico quantil versus quantil ou um gráfico q-q plot. O gráfico q-q teórico é o gráfico dos quantis de uma função de distribuição \(F\) versus os correspondentes quantis da função de distribuição \(G\), isto é, mostramos os pontos \(\Big(F^{-1}(p),G^{-1}(p)\Big)\) para \(0< p< 1\). Se as duas funções de distribuição forem idênticos, o gráfico q-q teórico será a diagonal principal, a linha de 45 graus através da origem. Se \(F(x)=G\big(\frac{x-\mu}{\sigma} \big)\), é facilmente visto que \(F^{-1}(p)=\mu+\sigma G^{-1}(p)\), de modo que o \(p\)-ésimo quantil de \(F\) e \(G\) tem uma relação linear. Assim, se duas distribuições diferirem apenas em localização e/ou escala, o gráfico teórico q-q será uma reta com inclinação \(\sigma\) e intercepto \(\mu\).
Em um problema de ajuste, normalmente há uma funço de distribuição de destino especificada, digamos \(F_0\). Então o q-q plot teórico é a plotagem de \(\Big(F_0^{-1}(p),F_X^{-1}(p)\Big) \), \(0 < p < 1\). Como o \(F_X\) é desconhecida, podemos estima-la utilizando a função de distribuição empírica baseada em uma amostra aleatória de tamanho \(n\), digamos, \(\widehat{F}_n\). Observando que esta função tem pulos apenas nos valores ordenados \( X_{(i)}\), o gráfico empírico q-q plot é simplesmente o gráfico de \(F_0^{-1}(i/n)\) no eixo horizontal versus \(\widehat{F}_n^{-1}(i/n)=X_{(i)}\) no eixo vertical, para \(i= 1,2,\cdots, n\). Como observado anteriormente, \(F_0\) é geralmente considerada como sendo uma forma padronizada da funçã de distribuiç:ão hipotética, de forma que para estabelecer o gráfico, locação e/ou escala, os parâmetros subjacentes não precisam ser especificados. Esta é uma vantagem do gráfico q-q plot.
As quantidades \(a_i=i/n\) são chamadas de posições de plotagem. Em \(i=n\), não há problema, pois dado que \(a_n=F_0^{-1}(1)=\infty\); as posições modificadas de plotagem foram consideradas, com vários objetivos. Uma escolha simples é \(a_i=i-0.5/n\); outras escolhas incluem \(a_i=i/n+1\) e \(a_i=(i-0.0375)/(n+0.25)\), sendo esta última altamente recomendada. O gráfico empírico q-q plot é então \(\Big(F_0^{-1}\big((i-0.0375)/(n+0.25)\big),X_{(i)} \Big)\). Para uma dada função de distribuição padronizada \(F_0\), a hipótese nula deste teste de bondade de ajuste \(F_X=F_0\) não é rejeitada se este gráfico for aproximadamente uma linha reta na origem. Afastamentos desta linha sugerem os tipos de diferenças que podem existir entre \(F_X\) e \(F_0\).
Seja \(X_1,X_2,\cdots,X_n\) uma amostra aleatóo de tamanho \(n\) de alguma distribuição desconhecida \(F\). Seja \(p\) um número real positivo satisfazendo \(0< p < 1 \) e \(\kappa_p(F)\) denotando o quantil de ordem \(p\) da distribuição \(F\), ou seja, \(\kappa_p(F)\) é tal que \(P\Big(X\leq \kappa_p(F)\Big)=p\) isto devido a que no seguinte estudo vamos considerar \(F\) absolutamente contínua.
O problema de posição consiste em verificar se \(H_0: \kappa_p(F)=\kappa_0\), sendo \(\kappa_0\) um valor dado, contra alguma das alternativas \(\kappa_p(F)>\kappa_0\), \(\kappa_p(F)<\kappa_0\) ou \(\kappa_p(F)\neq \kappa_0\). O problema de posição e simetria consiste em verificar se \(H_0: \kappa_{0.5}(F)=\kappa_0\) e \(F\) é simétrica contra \(H_0: \kappa_{0.5}(F)\neq \kappa_0\) ou \(F\) não é simétrica.
Seja \(X_1,X_2,\cdots,X_n\) uma amostra aleatória com função de densidade comum \(f\). O problema aqui é verificarmos \begin{equation} H_0: \kappa_p(f)=\kappa_0 \qquad H_1: \kappa_p(f)>\kappa_0, \end{equation} onde \(\kappa_p(f)\) é o quantil de ordem \(p\) para \(f\), \(0< p < 1\). Vejamos como construir a estatística de teste.
Seja \(i(X_1,X_2,\cdots,X_n)\) o número de elementos positivos em \(X_1-\kappa_0,X_2-\kappa_0,\cdots,X_n-\kappa_0\). Observemos que \(P(X_i=\kappa_0)=0\), desde que \(X_i\) seja uma variável aleatória do tipo contínuo. Pode ser demonstrado que o teste uniformemente mais poderoso para verificar \(H_0\) versus \(H_1\) é dado por \begin{equation} \varphi(x_1,x_2,\cdots,x_n)=\left\{ \begin{array}{rl} 1, & i(x_1,x_2,\cdots,x_n) > c, \\ \gamma , & i(x_1,x_2,\cdots,x_n) = c, \\ 0, & i(x_1,x_2,\cdots,x_n) < c, \end{array}\right. \end{equation} onde \(c\) e \(\gamma\) são escolhidos de forma que \begin{equation} \sum_{k=c}^n {n \choose i} q^i p^{n-i} + \gamma {n \choose c} q^c p^{n-c} = \alpha, \end{equation} com \(q=1-p\). Isto é devido a que, sob \(H_0\) verdadeira, \(\kappa_p(f)=\kappa_0\), de maneira que \( P(X\leq \kappa_0)=p\) e \(P(X\geq \kappa_0)=q\) e \( i(X)\sim Binomial(n,q)\). A mesma estatística de teste pode ser utilizada em qualquer outra situação, ou seja, utiliza-se também caso \(H_0: \kappa_p(f)\leq \kappa_0 \) versus \(H_1: \kappa_p(f)\geq \kappa_0\), \(H_0: \kappa_p(f)\geq \kappa_0 \) versus \(H_1: \kappa_p(f)\leq \kappa_0\) e \(H_0: \kappa_p(f)=\kappa_0\) contra \( H_1: \kappa_p(f)\neq \kappa_0\).
As expressões do p-valor para este teste podem ser obtidas de maneira geral quando \(p = 0.5\). Por exemplo, se a alternativa é de cauda superior \(H_1: \kappa_p(f)\geq \kappa_0\), o p-valor para o teste de sinal é dado pela probabilidade binomial na cauda superior \begin{equation} \sum_{i=i(x)}^n {n \choose i} 0.5^n, \end{equation} sendo \(i(x)=i(x_1,x_2,\cdots,x_n) \) o valor observado da estatística de teste. Poderíamos facilmente gerar tabelas para aplicar o teste de sinal exato para qualquer tamanho de amostra. No entanto, sabemos que a aproximação normal à binomial é especialmente boa quando \(p = 0.5\). Portanto, para valores moderados de \(n\) digamos, pelo menos 12, a aproximação normal pode ser usada para determinar as regiões de rejeição. Como esta é uma aproximação contínua a uma distribuição discreta, uma correção de continuidade de 0.5 pode ser incorporada aos cálculos. Por exemplo, para a alternativa, \(H_1: \kappa_{0.5}(f)\geq \kappa_0\), \(H_0\) é rejeitada para \(i(x_1,x_2,\cdots,x_n)\geq \kappa_\alpha \), sendo \(\kappa_\alpha\) satisfazendo \begin{equation} \kappa_\alpha = 0.5 n +0.5 +0.5\sqrt{n} z_\alpha\cdot \end{equation} Similarmente, o p-valor aproximado é \begin{equation} 1-\Phi\Big( \frac{\kappa_0-0.5-0.5 n}{\sqrt{0.25 n}} \Big)\cdot \end{equation} O teste do sinal para as diferentes hipótesis está programado no pacote DescTools, função SignTest.
O teste do sinal de amostra única descrito acima pode ser facilmente modificado para se aplicar à amostragem de uma população bivariada.
O teste de sinal perde informação, pois ignora a magnitude da diferença entre as observações e o quantil hipotético. O teste de postos sinalizados de Wilcoxon fornece um teste alternativo de posição e simetria que também leva em conta a magnitude dessas diferenças.
Seja \(X_1,X_2,\cdots,X_n\) uma amostra aleatória com função de distribuição \(F\) absolutamente contínua que é simétrica a respeito da mediana \(m\). O problema é testar \(H_0: m=m_0\) contra as alternativas usuais unilaterais ou bilaterais. Sem perda de generalidade, assumimos que \(m_0=0\). Então \(F(-x)=1-F(x)\) para todo \(x\in\mathbb{R}\). Para testar \(H_0: F(0)=\frac{1}{2}\) ou \(m=0\), primeiro organizamos \(|X_1|,|X_2|,\cdots,|X_n|\) em ordem crescente de magnitude e atribuímos postos \(1,2,\cdots,n\) mantendo-se a par dos sinais originais de \(X_i\). Por exemplo, se \(n=4\) e \(|X_2|< |X_4|< |X_1|< |X_3|\) o posto de \(|X_1|\) é 3, de \(|X_2|\) é 1, de \(|X_3|\) é 4 e de \(|X_4|\) é 2.
Definimos \begin{equation} \left\{ \begin{array}{rcl} T^+ & = & \mbox{soma dos postos dos } X \mbox{ positivos}, \\ T^- & = & \mbox{soma dos postos dos } X \mbox{ negativos} \end{array}\right.\cdot \end{equation} Então, considerando \(H_0\) verdadeira, experamos que \(T^+\) e \(T^-\) sejam o mesmo. Observe que \begin{equation} T^++T^- \, = \, \sum_{i=1}^n i \, = \, \dfrac{n(n+1)}{2}, \end{equation} de maneira que \(T^+\) e \(T^-\) são linearmente relacionados e oferecem critérios equivalentes. Definimos agora \begin{equation} Z_i \, = \, \left\{ \begin{array}{rcl} 1, & \mbox{caso} & X_i>0 \\ 0, & \mbox{caso} & X_i<0 \end{array}\right., \qquad i=1,2,\cdots,n, \end{equation} e escrevemos \(r(|X_i|)=r_i\), para o posto de \(|X_i|\). Então \(\displaystyle T^+=\sum_{i=1}^n r_iZ_i\) e \(\displaystyle T^-=\sum_{i=1}^n r_i(1-Z_i)\). Também, \begin{equation} T^+-T^- \, = \, -\sum_{i=1}^n r_i + 2\sum_{i=1}^n r_iZ_i \, = \, 2\sum_{i=1}^n r_iZ_i-\dfrac{n(n+1)}{2}\cdot \end{equation} As estatísticas \(T^+\) e \(T^-\) são conhecidas como estatísticas de Wilcoxon. Um grande valor de \(T\) ou, equivalentemente, um pequeno valor de \(T\) significa que a maioria dos grandes desvios de 0 são positivos e, portanto, rejeitamos \(H_0\) em favor da alternativa, \(H_1: m>0\).
Uma análise semelhante aplica-se às outras duas alternativas. Registramos os resultados da seguinte forma:
| \(H_0\) | \(H_1\) | Rejeitamos \(H_0\) se | ||
|---|---|---|---|---|
| \(m=0\) | \(m>0\) | \(T^+>c_1\) | ||
| \(m=0\) | \(m < 0\) | \(T^+< c_2\) | ||
| \(m=0\) | \(m \neq 0\) | \(T^+< c_3\) ou \(T^+> c_4\) | ||
Vamos encontrar agora a distribuicao de \(T^+\). Seja \begin{equation} Z_{(i)}=\left\{ \begin{array}{rl} 1, & \mbox{se o } |X_i| \mbox{ que tem posto } i \mbox{ é } >0, \\ 0, & \mbox{caso contrário} \end{array}\right. \end{equation} É claro que \(T^+=\sum_{i=1}^n iZ_{(i)}\). As variáveis aleatórias \(Z_{(1)},Z_{(2)},\cdots,Z_{(n)}\) tem por distribuição Bernoulli, são não correlacionadas mas não necessariamente igualmente distribuídas. Temos \begin{equation} \begin{array}{rcl} \mbox{E}\big( Z_{(i)} \big) & = & P\big( Z_{(i)} = 1\big) \, = \, P\big( [r(|X_i|)=i, \, X_j>0] \, \mbox{para algum } j\big) \\ & = & P\big( i\mbox{-ésima estatística de ordem em } |X_1|,|X_2|,\cdots,|X_n| \, \mbox{corresponde a um } X_j \, \mbox{positivo}\big) \\ & = & \displaystyle \int_0^\infty n{ n-1 \choose i-1} [F_{|X|}(u)]^{i-1}[1-F_{|X|}(u)]^{n-i}f(u)\mbox{d}u \\ & = & \displaystyle n{ n-1 \choose i-1}\int_0^\infty [F(u)-F(-u)]^{i-1}[1-F(u)+F(-u)]^{n-i} f(u)\mbox{d}u, \end{array} \end{equation} onde \(f\) é a função de densidade de \(X\). Além disso \begin{equation} \mbox{Var}\big( Z_{(i)} \big) \, = \, \mbox{E}\Big( Z_{(i)}\big( 1-\mbox{E}\big(Z_{(i)}\big) \big)\Big) \end{equation} e \begin{equation} \mbox{Cov}\big( Z_{(i)},Z_{(j)} \big) \, = \, 0, \qquad i\neq j\cdot \end{equation} Sob \(H_0\), \(X\) é simétrica a respeito de 0, de modo que \(F(0)=\frac{1}{2}\) e \(F(-u)=1-F(u)\), para todo \(u>0\). Então \begin{equation} \mbox{E}\big( Z_{(i)} \big) \, = \, n{ n-1 \choose i-1}\int_0^\infty \big(2F(u)-1\big)^{i-1}\big(2-2F(u)\big)^{n-i}f(u)\mbox{d}u\cdot \end{equation} Escolhendo \(\nu=2F(u)-1\), temos que \begin{equation} \mbox{E}\big( Z_{(i)} \big) \, = \, \frac{n}{2}{ n-1 \choose i-1}\int_0^1 \nu^{i-1}(1-\nu)^{n-i}\mbox{d}\nu \, = \, \frac{n}{2}{ n-1 \choose i-1} B(i, n-i+1) \, = \, \frac{1}{2}\cdot \end{equation}
Os momentos de \(T^+\), em geral, são dados por \begin{equation} \mbox{E}(T^+) \, = \, \sum_{i=1}^n i\mbox{E}\big( Z_{(i)} \big) \end{equation} e \begin{equation} \mbox{Var}(T^+) \, = \, \sum_{i=1}^n i^2\mbox{E}\Big( Z_{(i)}\big( 1-\mbox{E}\big(Z_{(i)}\big) \big)\Big)\cdot \end{equation} De maneira que, considerando \(H_0\) verdadeira, temos \begin{equation} \mbox{E}_{H_0}(T^+) \, = \, \frac{1}{2}\sum_{i=1}^n i \, = \, \frac{n(n+1)}{4} \end{equation} e \begin{equation} \mbox{Var}_{H_0}(T^+) \, = \, \frac{1}{4}\sum_{i=1}^n i^2 \, = \, \frac{n(n+1)(2n+1)}{24}\cdot \end{equation}
Observe que \(T^+=0\) se todas as diferenças tiverem sinais negativos e \(T^+=n(n+1)/2\) se todas as diferenças tiverem sinais positivos. Aqui, uma diferença significa uma diferença entre as observações e o valor postulado da mediana. \(T^+\) é completamente determinado pelos indicadores \(Z_{(i)}\), de modo que o espaço amostral possa ser considerado como um conjunto de \((z_1,z_2,\cdots,z_n)\), onde cada \(z_i\) é 0 ou 1, de cardinalidade \(2^n\).
Sob \(H_0\), \(m = m_0\) e cada arranjo é igualmente provável. Portanto \begin{equation} P_{H_0}(T^+=t)=\frac{\{\mbox{número de maneiras de atribuir sinais + ou - aos inteiros 1,2,..., n para que a soma seja t } \}}{2^n}\cdot \end{equation} Observemos que toda atribuição tem uma atribuição conjugada com sinais de mais e menos trocados, de modo que para este conjugado \(T^+\) é dado por \begin{equation} \sum_{i=1}^n i(1-Z_{(i)}) \, = \, \frac{n(n+1)}{2} \, - \, \sum_{i=1}^n iZ_{(i)}\cdot \end{equation} Assim, sob \(H_0\), a distribuição de \(T^+\) é simétrica em relação à média \(n(n+1)/4\).
 |
 |
|---|
Imagine uma fila de dez pessoas esperando para comprar um ingresso em uma sala de cinema em uma tarde de sábado, suponha que observemos o arranjo de cinco homens e cinco mulheres na fila como sendo H, M, H, M, H, M, H, M, H, M. Isso seria considerado um arranjo aleatório por gênero? Intuitivamente, a resposta é não, já que a alternância dos dois tipos de símbolos sugere mistura intencional por pares. Esse arranjo é um caso extremo, assim como a configuração H, H, H, H, H, M, M, M, M, M, como um agrupamento intencional. Nas situações menos extremas, a aleatoriedade de um arranjo pode ser testada estatisticamente usando a teoria das corridas.
Dada uma sequência ordenada de um ou mais tipos de símbolos, uma corrida é definida como sendo uma sucessão de um ou mais tipos de símbolos que são seguidos e processados por um símbolo diferente ou nenhum símbolo. As pistas para a falta de aleatoriedade são fornecidas por qualquer tendência dos símbolos de exibir um padrão definido na sequência. Tanto o número de realizações quanto os comprimentos das realizações, que obviamente estão inter-relacionados, devem refletir a existência de algum tipo de padrão. Os testes de aleatoriedade podem, portanto, ser baseados em qualquer critério ou em alguma combinação deles. Poucas corridas, muitas corridas, uma corrida de comprimento excessivo, muitas corridas de excesso de comprimento excessivo, etc. podem ser usadas como critérios estatísticos para rejeição da hipótese nula de aleatoriedade, uma vez que essas situações devem ocorrer raramente em uma sequência verdadeiramente aleatória.
A alternativa à aleatoriedade é muitas vezes simplesmente falta de aleatoriedade. Em um teste baseado no número total de realizações, tanto poucas quanto muitas corridas sugerem falta de aleatoriedade. Uma hipótese nula de aleatoriedade seria consequentemente rejeitada se o número total de realizações fosse muito grande ou muito pequeno. No entanto, as duas situações podem indicar diferentes tipos de falta de aleatoriedade. No exemplo do cinema, uma sequência com muitas realizações, tendendo a alternar os sexos, pode sugerir que o filme é popular entre adolescentes e jovens adultos, enquanto o outro arranjo extremo pode resultar se o filme é mais popular entre as crianças mais novas.
O teste de aleatoriedade é uma adição importante à teoria estatística, porque as bases teóricas para quase todas as técnicas clássicas, bem como os procedimentos livres de distribuição, começam com a suposição de uma amostra aleatória. Se essa suposição for válida, toda ordem sequencial é irrelevante. No entanto, se a aleatoriedade das observações for suspeita, as informações sobre ordem, que quase sempre estão disponíveis, podem ser usadas para testar uma hipótese de aleatoriedade. Esse tipo de análise também é útil em estudos de séries temporais e de controle de qualidade.
Os símbolos estudados para o padrão podem surgir naturalmente, como no exemplo do cinema ou podem ser impostos artificialmente. Assim, os testes de aleatoriedade são aplicáveis a dados qualitativos e quantitativos. No último caso, a dicotomia é geralmente efetuada comparando-se a magnitude de cada número com um ponto focal, comumente a mediana ou a média da amostra e nada se cada observação excede ou é excedida por este valor. Ambas as técnicas usam a informação sobre magnitudes relativas de números adjacentes na sequência ordenada pelo tempo. Essas técnicas, chamadas de teste de subidas e descidas e o teste de von Neumann, usam mais as informações disponíveis e são especialmente efetivas quando a alternativa para a aleatoriedade é uma tendência ou autocorrelação.
Suponhamos uma sequência ordenada de \(n\) elementos de dois tipos, \(n_1\) do primeiro tipo e \(n_2\) do segundo tipo, onde \(n_1 + n_2 = n\). Se \(r_1\) for o número de realizações de elementos do tipo 1 e se \(r_2\) for o número de realiazações do tipo 2, o número total de realizações na sequência será \(r = r_1 + r_2\). Para derivar um teste de aleatoriedade baseado na variável \(R\), o número total de realizações, precisamos da distribuição de probabilidade de \(R\) quando a hipótese nula de aleatoriedade for verdadeira.
A distribuição de \(R\) será encontrada determinando primeiro a distribuição conjunta de \(R_1\) e \(R_2\) e depois a distribuição de sua soma. Uma vez que sob a hipótese nula cada arranjo dos \(n_1 + n_2\) objetos é equiprovável, a probabilidade de que \(R_1 = r_1\) e \(R_2 = r_2\) é o número de arranjos distinguíveis de \(n_1 + n_2\) objetos com \(r_1\) corridas tipo 1 e \(r_2\) corridas de objetos do tipo 2 dividido pelo número total de arranjos distinguíveis, que é \(n!/n_1! n_2!\). Para a quantidade do numerador, o seguinte Lema de contagem pode ser usado.
Para obter uma sequência com execuções \(r_1\) dos objetos do tipo 1, \(n_1\) desses objetos devem ser colocados nas \(r_1\) células, o que pode ser feito de \({n_1-1 \choose r_1-1}\) maneiras diferentes. O mesmo raciocínio se aplica para obter \(r_2\) realizações dos outros \(n_2\) objetos. O número total de arranjos distintos começando com uma corrida do tipo 1 é o produto \({n_1-1 \choose r_1-1}{n_2-1 \choose r_2-1}\). Da mesma forma, para uma sequ≖ncia que começa com uma realização do tipo 2. Os blocos de objetos do tipo 1 e tipo 2 devem alternar e, consequentemente, ou \(r_1 = r_2 \pm 1\) ou \(r_1 = r_2\). Se \(r_1 = r_2 = 1\), a sequência deve começar com o tipo 1 de realização; se \(r_1 = r_2-1\), uma corrida do tipo 2 deve vir primeiro. Mas se \(r_1 = r_2\), a seqüência pode começar com uma sequência de qualquer tipo, então o número de arranjos diferenciáveis deve ser dobrado. Assim, provamos o seguinte resultado.
Usando este resultado, tabelas podem ser preparadas para testes de significância da hipótese nula de aleatoriedade. Por exemplo, se \(n_1 = 5\) e \(n_2 = 4\), temos \begin{equation} \begin{array}{ll} f_R(9)=\frac{\displaystyle {4 \choose 4}{3 \choose 3}}{\displaystyle {9 \choose 4}} \, = \, \frac{1}{126} \, = \, 0.008, & f_R(8)=\frac{\displaystyle 2{4 \choose 3}{3 \choose 3}}{\displaystyle {9 \choose 4}} \, = \, \frac{8}{126} \, = \, 0.063, \\ f_R(2)=\frac{\displaystyle 2{4 \choose 0}{3 \choose 0}}{\displaystyle {9 \choose 4}} \, = \, \frac{2}{126} \, = \, 0.016, & f_R(3)=\frac{\displaystyle {4 \choose 1}{3 \choose 0} + {4 \choose 0}{3 \choose 1}} {\displaystyle {9 \choose 4}} \, = \, \frac{7}{126} \, = \, 0.056\cdot \end{array} \end{equation} Para um teste bilateral que rejeita a hipótese nula para \(R \leq 2\) ou \(R \geq 9\), o nível exato de significância \(\alpha\) seria \(3/126 = 0.024\). Para a região crítica definida por \(R \leq 3\) ou \(R \geq 8\), \(\alpha = 18/126 = 0.143\). Quanto a todos os testes baseados em distribuições de probabilidade discretas, há um número finito de valores possíveis de \(\alpha\). Para um teste com nível de significância de no máximo 0.05, digamos, a primeira região crítica acima seria usada mesmo que o valor real de \(\alpha\) seja apenas 0.024.
O \(k\)-ésimo momento de \(R\) é \begin{equation} \begin{array}{rcl} \mbox{E}(R^k) & = & \displaystyle \sum_r r^k f_R(r) \\ & = & \frac{\displaystyle \sum_{r \mbox{ par}} 2r^k {n_1-1 \choose \frac{r}{2}-1}{n_2-1 \choose \frac{r}{2}-1} + \sum_{r \mbox{ ímpar}} \left[ {n_1-1 \choose \frac{r-1}{2}}{n_2-1 \choose \frac{r}{2}} + {n_1-1 \choose \frac{r-3}{2}}{n_2-1 \choose \frac{r-1}{2}}\right]}{\displaystyle {n_1+n_2 \choose n_1} } \end{array} \end{equation} O menor valor de \(r\) é sempre 2. Se \(n_1 = n_2\), o maior número de realizações ocorre quando os símbolos alternam, em cujo caso \(r = 2 n_1\). Se \(n_1 < n_2\), o valor máximo de \(r\) é \(2n_1 + 1\), uma vez que a sequência pode começar e terminar com um símbolo do tipo 2. Assumindo sem perda de generalidade que \(n_1 \leq n_2\), a faixa de soma para \(r\) é \(2 \leq r \leq 2n_1 + 1\). Considerando \(r = 2i\) para \(r\) par e \(r = 2i + 1\) para \(r\) ímpar, o intervalo de \(i\) é \(1 \leq i \leq n_1\).
Por exemplo, a experança de \(R\) seria \begin{equation} \begin{array}{rcl} \displaystyle {n_1+n_2 \choose n_1} \mbox{E}(R) & = & \displaystyle \sum_{i=1}^{n_1} 4i{n_1-1 \choose i-1}{n_2-1 \choose i-1} + \sum_{i=1}^{n_1} (2i+1){n_1-1 \choose i}{n_2-1 \choose i-1} + \sum_{i=1}^{n_1} (2i+1){n_1-1 \choose i-1}{n_2-1 \choose i}\cdot \end{array} \end{equation} Para avaliar essas três somas, os seguintes Lemas são úteis.
O processo algébrico de obtenção de \(\mbox{E}(R)\) é tedioso e será deixado como um exercício para o leitor. A variância de \(R\) pode ser encontrada avaliando o momento fatorial \(\mbox{E}\big(R(R-1)\big)\) de maneira similar.
Uma abordagem muito mais simples para encontrar os momentos de \(R\) é fornecida considerando \(R\) como a soma das variáveis indicadoras como segue para \(n = n_1 + n_2\). Consideremos \begin{equation} R = 1+I_2+I_3+\cdots+I_n, \end{equation} onde em uma sequência ordenada dos dois tipos de símbolos, definimos \begin{equation} I_k \, = \, \left\{ \begin{array}{ll} 1, & \mbox{ se o } k-\mbox{ésimo elemento } \neq \mbox{ do } (k-1)-\mbox{ésimo elemento} \\ 0, & \mbox { de outra forma}\end{array}\right.\cdot \end{equation} Então \(I_k\) é uma variável aleatária \(Bernoulli(p)\), sendo \(p=n_1n_2/{n \choose 2}\), assim \begin{equation} \mbox{E}(I_k) \, = \, \mbox{E}(I_k^2) \, = \, \frac{\displaystyle 2n_1n_2}{\displaystyle n(n-1)}\cdot \end{equation} Como \(R\) é uma combinação linear desses \(I_k\), temos \begin{equation} \mbox{E}(R) \, = \, 1+\sum_{k=2}^n \mbox{E}(I_k) \, = \, 1+\frac{2n_1n_2}{n_1+n_2}, \end{equation} também \begin{equation} \begin{array}{rcl} \mbox{Var}(R) & = & \displaystyle \mbox{Var}\Big( \sum_{k=2}^n I_k\Big) \, = \, (n-1)\mbox{Var}(I_k) \, + \, \sum_{2 \, \leq \, j \, \neq \, k \, \leq \, n} \mbox{Cov}(I_jI_k) \\ & = & \displaystyle (n-1)\mbox{E}(I_k^2) \, + \, \sum_{2 \, \leq \, j \, \neq \, k \, \leq \, n} \mbox{E}(I_jI_k) \, - \, (n-1)^2\mbox{E}^2(I_k) \end{array} \end{equation} Para avaliar os \((n-1)(n-2)\) momentos conjuntos do tipo \(\mbox{E}(I_jI_k)\) para \(j \neq k\), as opções de subscrito podem ser classificadas da seguinte forma:
Embora a função de densidade de \(R\) possa ser utilizada para encontrar sua distribuição exata quaisquer sejam os valores de \(n_1\) e \(n_2\), os cálculos são trabalhosos, a menos que \(n_1\) e \(n_2\) sejam pequenos. Para amostras grandes, uma aproximação para a distribuição nula pode ser usada o que dá resultados razoavelmente bons, desde que \(n_1\) e \(n_2\) sejam maiores que 10.
A fim de encontrar a distribuição assintótica, assumimos que o tamanho total da amostra \(n\) tende ao infinito de tal maneira que \(n_1/n\to\lambda\) e \(n_2/n\to 1-\lambda\), \(\lambda\) fixo e \(0 < \lambda < 1\). Para grandes amostras, a média e a variância de \(R\) são \begin{equation} \lim_{n\to\infty} \mbox{E}\left( \frac{R}{n}\right) \, = \, 2\lambda(1-\lambda) \qquad \mbox{e} \qquad \lim_{n\to\infty} \mbox{Var}\Big( \frac{R}{\sqrt{n}}\Big) \, = \, 4\lambda^2(1-\lambda)^2\cdot \end{equation}
Padronizando a variável aleatória obtemos \begin{equation} Z \, = \, \frac{R-2n\lambda(1-\lambda)}{2\sqrt{n}\lambda(1-\lambda)} \end{equation} e substituindo \(R\) em termos de \(Z\), obtemos a distribuição de \(R\) ou \(f_Z(z)\). Se os fatores na expressão resultante são avaliados pela fórmula de Stirling, o limite é \begin{equation} \lim_{n\to\infty} \ln\Big(f_Z(z)\Big) \, = \, -\ln\big(\sqrt{2\pi}\big) \, - \, \frac{1}{2}z^2, \end{equation} o que mostra que a função de probabilidade limite de \(Z\) é a densidade normal padrão. Este resultado foi obtido por Wald and Wolfowitz (1940).
Para um teste bilateral de tamanho \(\alpha\) usando a aproximação normal, a hipótese nula de aleatoriedade seria rejeitada quando \begin{equation} \left| \frac{R-2n\lambda(1-\lambda)}{2\sqrt{n}\lambda(1-\lambda)} \right|\leq z_{\alpha/2}, \end{equation} onde \(z_\gamma\) é um número satisfazendo que \(\Phi(z_\gamma)=1-\gamma\) ou, equivalentemente, \(z_\gamma\) é o \((1-\gamma)\)-ésimo quantil da distribuição normal padrão. A média e variância exatas de \(R\) foram obtidas e também podem ser usadas na formação da variável aleatória padronizada, já que a distribuição assintótica permanece inalterada. Estes resultados estão disponíveis na função runs.test no pacote tseries e na função runs.test no pacote randtests.
Outra maneira de testar a aleatoriedade é comparando a magnitude de cada elemento com a do elemento imediatamente anterior na sequência e computando assim a soma dos quadrados das desvalorizações dos pares de elementos sucessivos. Se as magnitudes desses elementos forem substituídas por suas respectivas classificações na sequência antes de computar a soma dos quadrados dos desvios sucessivos, podemos obter um teste não paramétrico.
Especificamente, seja a sequência de observações ordenada pelo tempo \(X_1,X_2,\cdots,X_n\). A estatística de teste \begin{equation} NM \, = \, \sum_{i=1}^{n-1} \big( \mbox{posto}(X_i)-\mbox{posto}(X_{i+1})\big)^2 \end{equation} como proposto por Bartels (1982). Um teste baseado em uma função desta estatística é a versão do teste de razão para aleatoriedade desenvolvido por von Neumann usando a teoria normal e é uma transformação linear do coeficiente de correlação serial por postos introduzido por Wald e Wolfowits (1943).
Pode-se mostrar que a estatística de teste \(NM\) varia entre \((n-1)\) e \((n-1)(n^2 + n-3)/3\) se \(n\) é par e entre \((n-1)\) e \([(n- 1) (n^2 + n-3)/3] -1\) se \(n\) for ímpar. A distribuição nula exata do \(NM\) pode ser encontrada por enumeração e é dada em Bartels (1982) para \(4 \leq n \leq 10\) sendo disponibilizada na função bartels.rank.test (Bartels Rank Test) no pacote randtests.
Para amostras maiores, a estatística de teste \begin{equation} RVN \, = \, \frac{\displaystyle\sum_{i=1}^{n-1} \big( \mbox{posto}(X_i)-\mbox{posto}(X_{i+1})\big)^2} {\displaystyle\Big( \sum_{i=1}^n \mbox{posto}(X_i)-\frac{n+1}{2}\Big)^2} \end{equation} é normalmente distribuído assintoticamente com média 2 e variância \(\displaystyle \frac{4(n-2)(5n^2-2n-9)}{5n(n+1)(n-1)^2}\), que é aproximadamente igual a \(\displaystyle\frac{20}{5n+7}\). Se não houver laços, o denominador de \(RVN\) é igual à constante \(\displaystyle\frac{n(n^2-1)}{12}\).
Geralmente, é relativamente simples elaborar uma estatística que mede a propriedade de interesse, mas é quase sempre difícil ou impossível determinar a distribuição dessa estatística. Os métodos estatísticos clássicos concentraram-se principalmente nas propriedades estatísticas dos estimadores que possuem uma forma fechada simples e que podem ser analisados matematicamente. Com exceção de algumas estatísticas importantes, mas simples, esses métodos envolvem, muitas vezes, hipóteses de modelos irrealistas. Essas limitações foram superadas nas últimas duas décadas do século XX com avanços nos computadores. Uma classe de procedimentos computacionalmente intensivos conhecidos como métodos de reamostragem fornecem inferências em uma ampla gama de estatísticas sob condições muito gerais. Métodos de reamostragem envolvem a construção de "populações" hipotéticas derivadas das observações, cada uma das quais pode ser analisada da mesma maneira para ver como as estatísticas dependem de variações aleatórias plausíveis nas observações. Reamostragem dos dados originais preserva quaisquer distribuições que estejam realmente presentes, incluindo efeitos de seleção como truncamento e censura.
Talvez o método de reamostragem mais antigo, em que se escolhe aleatoriamente repetidamente a metade dos dados e estima-se a estatística para cada amostra. A inferência sobre o parâmetro pode ser baseada no histograma da estatística reamostrada. Foi usado por Mahalanobis em 1946 sob o nome de amostras interpenetrantes. Uma variante importante é o método de Quenouille - Tukey chamado de jackknife. Para um conjunto de \(n\) dados construímos exatamente \(n\) conjuntos de dados hipotéticos, cada um com \(n-1\) pontos, cada um omitindo um ponto diferente. O mais importante dos métodos de reamostragem é chamado de bootstrap. Bradley Efron introduziu o método de bootstrap, também conhecido como reamostragem com substituição, em 1979. Aqui, gera-se um grande número de conjuntos de dados, cada um com \(n\) pontos de dados extraídos aleatoriamente dos dados originais. A restrição é que cada desenho é feito a partir de todo o conjunto de dados, portanto, um conjunto de dados simulado provavelmente perderá alguns pontos e terá duplicatas ou triplicatas de outros. Assim, o bootstrap pode ser visto como um método de Monte Carlo para simular dados existentes, sem qualquer suposição sobre a população subjacente.
O jackknife fornece uma abordagem de propósito geral para estimar o viés e a variância ou erro padrão de um estimador. Suponha que \(\widehat{\theta}\) seja um estimador de \(\theta\) baseado na amostra aleatória \(X_1,X_2,\cdots,X_n\); \(\theta\) poderia ser um parâmetro desconhecido de algum modelo paramétrico ou \(\theta\) poderia ser um parâmetro funcional da função de distribuição comum \(F\) dos \(X_i\), caso em que \(\theta=\theta(F)\). O jackknife é particularmente útil quando os métodos padrão para calcular viés e variação não podem ser aplicados ou são difíceis de aplicar. Dois desses exemplos são dados a seguir.
O nome "jackknife" foi originalmente usado por Tukey (1958) para sugerir uma técnica de ampla utilidade como um substituto para técnicas mais especializadas, da mesma forma que jackknife pode ser usado como um substituto para uma variedade de ferramentas mais especializadas embora, na realidade, um jackknife não é uma ferramenta particularmente versátil. Referências mais completas sobre o jackknife são as monografias de Efron (1982) e Efron e Tibshirani (1993).
O estimador jackknife de viés foi desenvolvido por Quenouille (1949), embora ele não se referisse a ele como o jackknife. A idéia básica por trás dos estimadores jackknife de vício e variância está em recomputar o estimador do parâmetro usando todas as observações.
Suponha que \(\widehat{\theta}\) seja um estimador de um parâmetro \(\theta\) com base na amostra aleatória \(X_1,\cdots,X_n\), \(\widehat{\theta}=\widehat{\theta}(X)\). Por exemplo, \(\widehat{\theta}=\theta(\widehat{F}_n)\). O método proposto por Quenouille para estimar o vício de \(\widehat{\theta}\) é baseado na exclusão sequencial de uma única observação \(X_i\) e recalculando \(\widehat{\theta}\) com base em \(n-1\) observações. Suponha que \begin{equation} \mbox{E}(\widehat{\theta}) \, = \, \theta \, + \, b(\widehat{\theta}), \end{equation} onde \(b(\widehat{\theta})\) é o vício de \(\widehat{\theta}\). Seja \(\widehat{\theta}_{-i}\) o estimador de \(\theta\) avaliado na amostra depois de deletada \(X_i\), ou seja, \begin{equation} \widehat{\theta}_{-i}=\widehat{\theta}(X_1,\cdots,X_{i-1},X_{i+1},\cdots,X_n)\cdot \end{equation} Definamos agora por \(\widehat{\theta}_*\) a média de \(\widehat{\theta}_{-1},\widehat{\theta}_{-2},\cdots,\widehat{\theta}_{-n}\), \begin{equation} \widehat{\theta}_* \, = \, \frac{1}{n}\sum_{i=1}^n \widehat{\theta}_{-i}\cdot \end{equation}
O estimador jackknife do vício é então \begin{equation} \widehat{b}(\widehat{\theta}) \, = \, (n-1)(\widehat{\theta}_*-\widehat{\theta})\cdot \end{equation} A versão corrigida de viés de \(\widehat{\theta}\) pode ser construída subtraindo-se \(\widehat{b}(\widehat{\theta})\) de \(\widehat{\theta}\). Vamos mostrar abaixo que este procedimento reduz o viés de \(\widehat{\theta}\).
O raciocínio teórico por trás de \(\widehat{b}(\widehat{\theta})\) assume que \(\mbox{E}(\widehat{\theta})\) pode ser expressa como uma série envolvendo potências de \(1/n\); por simplicidade, vamos primeiro assumir que para qualquer \(n\) \begin{equation} \mbox{E}(\widehat{\theta}) \, = \, \theta \, + \, \frac{\alpha_1(\theta)}{n}, \end{equation} onde \(\alpha_1(\theta)\) pode depender de \(\theta\) ou da distribuição de \(X_i\) mas não do tamanho da amostra \(n\); neste caso, \(b(\widehat{\theta})=\alpha_1(\theta)/n\). Dado que \(\widehat{\theta}_{-i}\) é baseado em \(n-1\) observações para cada \(i\), segue que \begin{equation} \mbox{E}(\widehat{\theta}_*) \, = \, \frac{1}{n}\sum_{i=1}^n \mbox{E}(\widehat{\theta}_{-1}) \, = \, \theta + \frac{\alpha_1(\theta)}{n-1}\cdot \end{equation} Então \begin{equation} \mbox{E}(\widehat{\theta}-\widehat{\theta}_*) \, = \, \frac{\alpha_1(\theta)}{n} \, - \, \frac{\alpha_1(\theta)}{n} \, = \, \frac{\alpha_1(\theta)}{n(n-1)}, \end{equation} e assim \(n(n-1)(\widehat{\theta}-\widehat{\theta}_*)\) é um estimador não viciado de \(b(\widehat{\theta})\). No caso geral, teremos \begin{equation} \mbox{E}(\widehat{\theta}) \, = \, \theta \, + \, \frac{\alpha_1(\theta)}{n} + \frac{\alpha_2(\theta)}{n^2} + \frac{\alpha_3(\theta)}{n^3} + \cdots \end{equation} ou \begin{equation} b(\widehat{\theta}) \, = \, \frac{\alpha_1(\theta)}{n} + \frac{\alpha_2(\theta)}{n^2} + \frac{\alpha_3(\theta)}{n^3} + \cdots, \end{equation} onde \(\alpha_1(\theta), \alpha_2(\theta), \alpha_3(\theta), \cdots\) podem depender de \(\theta\) ou da distribuição de \(X_i\), mas não de \(n\). Mais uma vez, segue-se que \begin{equation} \mbox{E}(\widehat{\theta}_*) \, = \, \frac{1}{n}\sum_{i=1}^n \mbox{E}(\widehat{\theta}_{-i}) \, = \, \theta \, + \, \frac{\alpha_1(\theta)}{n-1} + \frac{\alpha_2(\theta)}{(n-1)^2} + \frac{\alpha_3(\theta)}{(n-1)^3} + \cdots, \end{equation} lembrando que cada \(\widehat{\theta}_{-i}\) depende de \(n-1\) observações. Assim, a esperança do viés do estimador jackknife é \begin{equation} \begin{array}{rcl} \mbox{E}\big(\widehat{b}(\widehat{\theta})\big) & = & (n-1)\big( \mbox{E}(\widehat{\theta}_*) - \mbox{E}(\widehat{\theta})\big) \\ & = & \displaystyle \frac{\alpha_1(\theta)}{n} + \frac{(2n-1)\alpha_2(\theta)}{n^2(n-1)} + \frac{(3n^2-3n+1)\alpha_3(\theta)}{n^3(n-1)^2} + \cdots \end{array} \end{equation}
Podemos ver acima que \(\widehat{b}(\widehat{\theta})\) não é um estimador não-viciado de \(b(\widehat{\theta})\) como era no caso simples considerado anteriormente. No entanto, observe que o primeiro termo de \(\mbox{E}\big(\widehat{b}(\widehat{\theta})\big)\), a saber \(\alpha_1(\theta)/n\), concorda com o de \(b(\widehat{\theta})\). Assim, se definirmos \begin{equation} \widehat{\theta}_{jack} \, = \, \widehat{\theta} - b(\widehat{\theta}) \, = \, n\widehat{\theta} - (n-1)\widehat{\theta}_* \end{equation} como sendo o estimador jackknife com correção de vício, segue que \begin{equation} \begin{array}{rcl} \mbox{E}\big(\widehat{\theta}_{jack}\big) & = & \theta + \displaystyle \frac{\alpha_2(\theta)}{n(n-1)} - \frac{(2n-1)\alpha_3(\theta)}{n^2(n-1)^2} + \cdots \\ & \approx & \theta + \displaystyle \frac{\alpha_2(\theta)}{n^2} - \frac{2\alpha_3(\theta)}{n^3} + \cdots \end{array} \end{equation} para \(n\) grande. Desde que \(1/n^2, 1/n^3, \cdots\) convergem a zero mais rápido do que \(1/n\) tende a zero, quando \(n\) fica grande, segue-se que o viés de \(\widehat{\theta}_{jack}\) é menor que o viés de \(\widehat{\theta}\) para \(n\) suficientemente grande. No caso em que \begin{equation} \mbox{E}(\widehat{\theta}) \, = \, \theta + \frac{\alpha_1(\theta)}{n}, \end{equation} de modo a \(\alpha_2(\theta) \, = \, \alpha_3(\theta) \, = \cdots \, = 0\), \(\widehat{\theta}_{jack}\) será não-viciado.
Este ultimo exemplo aponta uma das desvantagens de usar qualquer método de propósito geral como o jackknife, ou seja, em situações específicas muitas vezes é possível melhorar o estimador com um método adaptado especificamente para a situação em questão. Remover o viés em \(\widehat{\theta}=X_{(n)}\) multiplicando-o por \((n+1)/n\) depende do fato de que a forma da densidade seja conhecida. Suponha, em vez disso, que o intervalo dos \(X_i\) ainda seja \([0,\theta]\), mas que a densidade \(f\) seja desconhecida para \(0\leq x\leq \theta\). Então \(X_{(n)}\) ainda é um estimador razoável de \(\theta\) e sempre o subestima. No entanto, \((n+1)X_{(n)}/n\) não precisa ser não viciado e, de fato, pode ser mais severamente influenciado do que \(X_{(n)}\). No entanto, o estimador jackknife \begin{equation} \widehat{\theta}_{jack} = X_{(n)}+\frac{n-1}{n}\big( X_{(n)}-X_{(n-1)}\big), \end{equation} terá um viés menor que \(X_{(n)}\) e pode ser preferível a \(X_{(n)}\) nessa situação.
O estimador jackknife de vício usa os estimadores \(\widehat{\theta}_{-1},\cdots,\widehat{\theta}_{-n}\), que usam todas as observações, exceto uma em seu cálculo para construir um estimador de viés de um estimador \(\widehat{\theta}\). Tukey (1958) sugeriu um método para estimar \(\mbox{Var}(\widehat{\theta})\) que usa \(\widehat{\theta}_{-1},\cdots,\widehat{\theta}_{-n}\). O estimador jackknife de Tukey de \(\mbox{Var}(\widehat{\theta})\) é \begin{equation} \widehat{\mbox{Var}}(\widehat{\theta}) \, = \, \frac{n-1}{n}\sum_{i=1}^n (\widehat{\theta}_{-i}-\widehat{\theta}_*)^2, \end{equation} onde, como antes \(\widehat{\theta}_{-i}\) é o estimador avaliado usando todas as observaçães, exceto \(X_i\) e \begin{equation} \widehat{\theta}_* \, = \, \frac{1}{n}\sum_{i=1}^n \widehat{\theta}_{-i}\cdot \end{equation}
A fórmula para o estimador da variância jackknife é um tanto não intuitiva. Ao derivar a fórmula, Tukey assumiu que o estimador \(\widehat{\theta}\) pode ser bem aproximado por uma média de variáveis aleatórias independentes; essa suposição é válida para uma ampla variedade de estimadores, mas não é verdadeira para alguns estimadores, por exemplo, máximo ou mínimo de amostra. Mais precisamente, Tukey assumiu que \begin{equation} \widehat{\theta} \approx \frac{1}{n}\sum_{i=1}^n \phi(X_i), \end{equation} o qual sugere que \begin{equation} \mbox{Var}\widehat{\theta} \approx \frac{1}{n}\mbox{Var}\big(\phi(X_1)\big)\cdot \end{equation} No caso em que o parâmetro de interesse \(\theta\) é um parâmetro funcional da função de distribuição \(F\), isto é, \(\theta = \theta(F)\), a função \(\phi(\cdot) - \theta(F)\) é tipicamente a curva de influência de \(\theta(F)\).
Em geral, não conhecemos a função \(\phi(x)\), portanto não podemos usar diretamente a fórmula acima. No entanto, é possível encontrar substitutos razoáveis para \(\phi(X_1),\cdots,\phi(X_n)\). Usando os estimadores \(\widehat{\theta}_{-i}\), \(i=1,\cdots,n\) e \(\widehat{\theta}\), definimos pseudovalores \begin{equation} \Phi_i=\widehat{\theta}+(n-1)(\widehat{\theta}-\widehat{\theta}_{-i}), \end{equation} para \(i=1,\cdots,n\) que essencialmente desempenham o mesmo papel que o \(\phi(X_i)\) acima. No caso em que \(\theta=\theta(F)\), \((n−1)(\widehat{\theta}-\widehat{\theta}_{-i})\) é uma tentativa de estimar a curvatura de \(\theta(F)\) em \(x=X_i\). No caso em que \(\widehat{\theta}\) é exatamente a média amostral \begin{equation} \widehat{\theta}=\frac{1}{n}\sum_{i=1}^n \phi(X_i), \end{equation} é fácil mostrar que \(\Phi_i = \phi(X_i)\) e assim a conexão entre \(\Phi_i\) e \(\phi(X_i)\) é clara neste caso simples. Podemos então tomar a variância da amostra dos pseudovalores \(\Phi_i\) como sendo uma estimativa da variância de \(\phi(X_1)\) e usá-lo para estimar a variância de \(\widehat{\theta}\). Note que \begin{equation} \frac{1}{n}\sum_{i=1}^n \Phi_i \, = \, n\widehat{\theta}-\frac{n-1}{n}\sum_{i=1}^n \widehat{\theta}_{-i} \, = \, n\widehat{\theta}-(n-1)\widehat{\theta}_* \, = \, \widehat{\theta}_{jack}, \end{equation} onde \(\widehat{\theta}_{jack}\) é a versão de \(\widehat{\theta}\) com correção de viés. A variáncia amostral dos \(\Phi_i\) é \begin{equation} \frac{1}{n-1}\sum_{i=1}^n (\Phi_i-\phi)^2 \, = \, \frac{1}{n-1}\sum_{i=1}^n\big((n-1)(\widehat{\theta}_*-\widehat{\theta}_{-i})\big)^2 \, = \, (n-1)\sum_{i=1}^n (\widehat{\theta}_*-\widehat{\theta}_{-i})^2\cdot \end{equation}
Agora obtemos o estimador jackknife da variância dividindo a variância amostral de cada \(\Phi_i\) por \(n\): \begin{equation} \widehat{\mbox{Var}}(\widehat{\theta}) = \frac{n-1}{n}\sum_{i=1}^n (\widehat{\theta}_*-\widehat{\theta}_{-i})^2\cdot \end{equation} Deve-se notar que o estimador jackknife da variância não funciona em todas as situações. Uma dessas situações é a mediana amostral. O problema aqui parece ser o fato de que a curva de influência da mediana é definida apenas para distribuições contínuas e, portanto, é difícil de aproximar adequadamente em amostras finitas.
| 3841 | 7084 | 7254 | 15228 | 18042 | 19089 |
| 22588 | 23972 | 25694 | 27592 | 27927 | 31576 |
| 32528 | 32921 | 33724 | 36887 | 37776 | 37992 |
| 39464 | 40506 | 44516 | 46538 | 51088 | 51955 |
| 54339 | 57935 | 75137 | 82612 | 83381 | 84741 |
| Rendimentos antes dos impostos. | |||||
Utilizando o princípio de substituição o estimador de \(\theta(F)\) é \begin{equation} \widehat{\theta} \, = \, \theta(\widehat{F}_n) \, = \, \frac{1}{\displaystyle \sum_{i=1}^{30} X_i}\sum_{i=1}^{30} \Big( \frac{2i-1}{30}-1\Big)X_{(i)}, \end{equation} sendo \(X_{(1)}\leq X_{(2)}\leq \cdots \leq X_{(30)}\) as estatástica de ordem de \(X_1,\cdots,X_n\).
Para os dados na tabela, a estimativa de \(\theta(\widehat{F}_n)\) é 0.311. O erro padrão desta estimativa pode ser estimado usando o jackknife. As estimativas dos \(\widehat{\theta}_{-i}\) de \(\theta(\widehat{F}_n)\) são dadas na tabela abaixo.
| 0.2912 | 0.2948 | 0.2950 | 0.3028 | 0.3055 | 0.3064 |
| 0.3092 | 0.3103 | 0.3115 | 0.3127 | 0.3129 | 0.3148 |
| 0.3153 | 0.3154 | 0.3157 | 0.3166 | 0.3168 | 0.3168 |
| 0.3170 | 0.3170 | 0.3169 | 0.3167 | 0.3161 | 0.3159 |
| 0.3152 | 0.3140 | 0.3069 | 0.3033 | 0.3028 | 0.3020 |
| Valores de \(\widehat{\theta}_{-i}\) obtidos por omissão da entrada correspondente na tabela anterior. | |||||
O estimador jackknife do desvio padrão de \(\widehat{\theta}\) é \begin{equation} \widehat{\mbox{se}}(\widehat{\theta}) \, = \, \frac{29}{30}\sum_{i=1}^{30} (\widehat{\theta}_*-\widehat{\theta}_{-i})^2 \, = \, 0.0398, \end{equation} onde \(\widehat{\theta}_*=0.310\) é a média de \(\widehat{\theta}_{-1},\cdots,\widehat{\theta}_{-30}\).
A importância do bootstrap surgiu durante a década de 1980, quando o estudo matemático demonstrou que ele fornece estimativas quase ótimas da distribuição de muitas estatísticas sob uma ampla gama de circunstâncias. Em vários casos, o método produz melhores resultados do que aqueles obtidos pela teoria clássica da aproximação normal. No entanto, deve-se alertar que o bootstrap não é a solução para todos os problemas. A teoria desenvolvida nas décadas de 1980 e 1990 mostra que o bootstrap falha em algumas situações "não-suaves". Por isso, deve-se ter cautela e resistir à tentação de usar o método de forma inadequada.
Como os computadores se tornaram mais poderosos, o bootstrap, assim como os procedimentos de reamostragem em geral ganharam uso generalizado. O bootstrap é uma ferramenta geral usada para medir o erro em uma estimativa ou a significância de um teste de hipótese. Aqui demonstramos a utilidade do bootstrap para uma variedade de problemas, embora ainda apenas arranhemos a superfície; o leitor interessado em um tratamento completo é referido a Efron e Tibshirani (1993) ou o de Davison e Hinkley (1997). Ilustramos a como encontrar intervalos de confiança e p-valores para os problemas de posição de uma amostra e outros.
Para fixar ideias, lembre-se que o histograma da amostra é frequentemente usado para fornecer o contexto da distribuição da variável aleatória, por exemplo, localização, variabilidade, forma. Uma maneira de pensar no bootstrap é como um procedimento para fornecer algum contexto para a distribuição amostral de uma estatística. Uma amostra bootstrap é simplesmente uma amostra da amostra original obtida com reposição. A ideia é que, se a amostra é representativa da população, ou mais concretamente, se o histograma ou o estimador kernel da função de densidade da amostra se assemelha à função de densidade da variável aleatória, então a amostragem da amostra é representativa da amostragem da população. Fazê-lo repetidamente produzirá uma estimativa da distribuição amostral da estatística.
Seja \(X = (X_1,\cdots, X_n)\) uma amostra aleatária extraída de uma distribuição populacional desconhecida \(F\). Suponha que \(T_n(X)\) seja um bom estimador de \(T(F)\), um parâmetro de interesse. O interesse reside em avaliar sua precisão na previsão. Determinar os intervalos de confiança para \(T(F)\) requer conhecimento da distribuição amostral \(G_n\) de \(T_n(X)-T(F)\), isto é, \begin{equation} G_n(x) = P\big(T_n(X)-T(F)\leq x\big), \end{equation} para todo \(x\).
Por exemplo, a média amostral \(\overline{X} = \frac{1}{n}\sum_{i=1}^n X_i\) é um bom estimador da esperança populacional \(\mu\). Para obter o intervalo de confiança para \(\mu\), devemos encontrar a distribuição amostral de \(\overline{X}-\mu\), que depende da forma e outras características da distribuição desconhecida \(F\).
A teoria estatística clássica usa o Teorema do Limite Central como aproximação normal para a distribuição amostral. Por exemplo, se \((X_1,Y_1),\cdots,(X_n,Y_n)\) denotam observações de uma população normal bivariada, então o estimador de máxima verossimilhança do coeficiente de correlação \(\rho\) é dado pelo coeficiente de correlação de Pearson amostral \begin{equation} \widehat{\rho} = \frac{\displaystyle \sum_{i=1}^n (X_iY_i-\overline{X}\overline{Y})} {\displaystyle \sqrt{\big(\sum_{i=1}^n (X_i-\overline{X})^2 \big)\big(\sum_{i=1}^n (Y_i-\overline{Y})^2 \big)}}\cdot \end{equation}
Para estatísticas com distribuições assimétricas, como a de \(\widehat{\rho}\), a teoria clássica sugere transformações de variáveis. Neste caso, a transformação \(Z\) de Fisher dada por \begin{equation} Z = \frac{\sqrt{n-3}}{2}\Big( \ln\Big(\frac{1+\widehat{\rho}}{1-\widehat{\rho}}\Big)-\ln\Big(\frac{1+\rho}{1-\rho}\Big)\Big), \end{equation} dá uma melhor aproximação à normal. Esta aproximação corrige a assimetria e é melhor que a aproximação à normal de \(\sqrt{n}(\widehat{\rho}-\rho)\). O método de bootstrap, quando usado adequadamente, evita transformações levando em conta a assimetria da distribuição amostral.
O método de bootstrap presume que, se \(\widehat{F}_n\) é uma boa aproximação da distribuição da população desconhecida \(F\), então o comportamento das amostras de \(\widehat{F}_n\) se assemelha ao dos dados originais. Aqui \(\widehat{F}_n\) pode ser a função de distribuição empírica da amostra aleatória \(X_1,\cdots,X_n\) ou um estimador paramétrico da função \(F\). Uma vez que \(\widehat{F}_n\) é fornecido, os conjuntos de dados \(X^* = (X_1^*,\cdots,X_n^*)\) são reamostrados a partir de \(\widehat{F}_n\) e a estatística \(T_n(X^*)\) é computada para cada reamostra.
Sob condições muito gerais pode-se demonstrar que a diferença entre a distribuição amostral \(G_n\) de \(T_n(X)-T(F)\) e a distribuição bootstrap \(G_b\), isto é, a distribuição de \(T_n(X^*)-T(\widehat{F}_n)\) é insignificante. \(G_b\) pode ser usado para extrair inferências sobre o parâmetro \(T(F)\) no lugar do desconhecido \(G_n\). Em princípio a distribuição de bootstrap, obtida pelo histograma ou pelo estimador kernel de densidades, \(G_b\) é completamente conhecida, pois é construída inteiramente a partir dos dados originais. No entanto, para obter a distribuição completa de bootstrap, é necessário calcular as estatísticas para quase todas as \(n^n\) amostras possíveis bootstrap. Para o exemplo simples da média amostral, presumivelmente, é necessário computar \begin{equation} \begin{array}{rcl} X_1^{*(1)},\cdots,X_n^{*(1)}, & & r_1=\overline{X}^{*(1)}-\overline{X} \\ X_1^{*(2)},\cdots,X_n^{*(2)}, & & r_2=\overline{X}^{*(2)}-\overline{X} \\ \ddots & \ddots & \ddots \\ X_1^{*(n^n)},\cdots,X_n^{*(n^n)}, & & r_{n^n}=\overline{X}^{*(n^n)}-\overline{X} \\ \end{array} \end{equation}
A distribuição bootstrap dada pelo histograma ou pelo estimador kernel de densidade de \(r_1,\cdots,r_{n^n}\). Mesmo para \(n = 10\) dados, \(n^n\) acaba por ser dez bilhões. Na prática, a estatística de interesse, \(T_n(X^*)-T(\widehat{F}_n)\) é calculada para um número \(N\), digamos \(N = n\log^2(n)\), de novas amostras e sua distribuição bootstrap construída.
O bootstrap mais popular e simples é o bootstrap não paramétrico, onde a reamostragem com reposição é baseada na função de distribuição empírica da amostra aleatória original. Isto dá pesos iguais para cada um dos dados originais. A tabela abaixo fornece versões bootstrap de algumas estatísticas comumente usadas. No caso do estimador de razão e do coeficiente de correlação, os pares de dados são reamostrados a partir dos pares de dados originais \((X_i,Y_i)\).
| Estatística | Versão bootstrap |
| Média: \(\overline{X}\) | \(\overline{X}^*\) |
| Variância: \(\displaystyle \frac{1}{n}\sum_{i=1}^n (X_i-\overline{X})^2\) | \(\displaystyle \frac{1}{n}\sum_{i=1}^n (X_i^*-\overline{X}^*)^2\) |
| Estimador da razão: \(\frac{\displaystyle \overline{X}}{\displaystyle \overline{Y}}\) | \(\frac{\displaystyle \overline{X}^*}{\displaystyle \overline{Y}^*}\) |
| Coeficiente de correlação: | |
| \(\frac{\displaystyle \sum_{i=1}^n (X_iY_i-\overline{X}\overline{Y})} {\displaystyle \sqrt{\big(\sum_{i=1}^n (X_i-\overline{X})^2 \big)\big(\sum_{i=1}^n (Y_i-\overline{Y})^2 \big)}}\) | \(\frac{\displaystyle \sum_{i=1}^n (X_i^*Y_i^*-\overline{X}^*\overline{Y}^*)} {\displaystyle \sqrt{\big(\sum_{i=1}^n (X_i^*-\overline{X}^*)^2 \big)\big(\sum_{i=1}^n (Y_i^*-\overline{Y}^*)^2 \big)}}\) |
| Estatísticas e suas versões bootstrap. | |
O conceito de quantidade pivotal é muito importante para intervalos de confiança. Por exemplo, o fator de escala \(\overline{X}-\mu\) depende do desvio padrão \(\sigma\) ou de seu estimador. É possível obter intervalos de confiança ou intervalos aproximados de confiança para \(\mu\), se \(P\big(\overline{X}-\mu\big)/\sigma < x)\) não depende de \(\mu\) e \(\sigma\). A menos que a distribuição limite esteja livre dos parâmetros desconhecidos, uma vez que não pode ser invertida para obter intervalos de confiança. Assim, é importante concentrar-se em quantidades pivotais ou aproximadamente pivotais, a fim de obter intervalos de confiança confiáveis para o parâmetro de interesse.
Uma função \(T_n(X;F)\) é pivotal, se sua distribuição for livre de parâmetros desconhecidos de \(F\). No caso, \(X_i\sim N(\mu,\sigma^2)\), então \(T_n(X;F)=\sqrt{n}(\overline{X}-\mu)/ s_n\) é pivotal. No caso não normal, é aproximadamente pivotal. Para obter o intervalo de confiança bootstrap para \(\mu\), calculamos \(\sqrt{n}(\overline{X}^{*(j)}-\overline{X})/ s_n\) para \(N\) amostras bootstrap e organizamos os valores em ordem crescente \begin{equation} h_1\leq h_2\leq \cdots \leq h_N\cdot \end{equation}
Pode-se então ler do histograma (digamos) o intervalo de confiança de 90\% do parâmetro. Ou seja, o intervalo de confiança de 90\% para \(\mu\) é dado por \begin{equation} \overline{X}-h_m\frac{s_n}{\sqrt{n}}\leq \mu\leq \overline{X}-h_k\frac{s_n}{\sqrt{n}}, \end{equation} onde \(k = [0.5 N]\) e \(m = [0.95 N]\). Babu & Singh (1983) mostraram que \(N=n \log^2(n)\) iterações bootstrap seriam suficientes.
| Número de caras | 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|---|
| Frequência | 16 | 48 | 55 | 33 | 8 | |
| Ano | 1970 | 1971 | 1972 | 1973 | 1974 | 1975 | 1976 | 1977 | 1978 | 1979 | 1980 | 1981 | 1982 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Número de turistas | 12.362 | 12.739 | 13.057 | 13.955 | 14.123 | 15.698 | 17.523 | 18.610 | 19.842 | 20.310 | 22.500 | 23.080 | 21.916 |
| Mês | Janeiro | Fevereiro | Março | Abril | Maio | Junho | Julho | Agosto | Setembro | Outubro | Novembro | Dezembro |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| No. títulos | 19 | 23 | 20 | 17 | 18 | 20 | 22 | 24 | 25 | 28 | 30 | 21 |
| Candidato | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sexo | H | H | M | H | M | M | M | H | M | M | M | H | H | H | H | M |
| QI | 125 | 127 | 128 | 132 | 133 | 135 | 136 | 137 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 |