Histórico das aulas do curso

• 14/08
  • Manhã: apresentação, informações sobre o curso, percepções sobre geoestatística. Introdução ao programa R e ao pacote geoR. Leitura de dados, formato geodata e análises exploratórias.
  • Tarde: dependência especial: correlogramas e variogramas. Interpolação espacial (krigagem) e mapas de predição. Outros formados de dados espaciais (dados de área e de processos pontuais).
  • Atividades:
    1. Instalar o programa R e o pacote geoR
    2. Refazer o exemplo trabalhado em sala de aula
       1. Arquivo de dados (formato texto)
       2. Arquivo de comandos
    3. Verificar outros conjuntos de dados disponíveis no pacote geoR com o comando

       data(package="geoR")

       e efetuar análises descritivas atentando as características a serem observadas comentadas em aula (distribuição e assimetria, dados atípicos, tendências com coordenadas e covariáveis, possível padrão espacial)
    4. Obter outro conjunto de dados geoestatísticos (seu próprio ou em alguma fonte - web etc), carregar no R e efetuar análises
    5. Reproduzir e discutir as análises feitas com os comandos a seguir:
       1. arquivo de dados e de comandos

• 15/08
  • Manhã: atividades computacionas
  • Tarde: modelos com covariaveis - tendências com coordenadas e com covariáveis
    • arquivos utilizados:
      1. ca20
      2. definição de bordas
      3. wolfcamp revisado

• 21/08
• Discussão sobre variogramas
• Extensões dos modelos considerando covariáveis e transformações
• Apresentação e discussão de trabalhos, dados e projetos de participantes
• 22/08
  • Manhã
    • alguns modelos para dados de precipitação no PR
    • alguns modelos para dados Ca20
    • Exemplo de código básico para predição espacial (arquivo de comandos), incluindo exportação dos resultados
    • Um exemplo mais completo de comandos para análise
      • arquivo de dados utilizados no arquivo de comandos
  • Tarde
    • além de krigagem: Simulações da preditiva (condicionais)
    • arquivo de comandos atualizado

• 18/09
  • Manhã:
    1. simulação e funções de correlação
    2. estimação por verossimilhança
  • Tarde
    1. Predição espacial e efeitos do modelo na predição
    2. inferência e predição Bayesiana
• 19/09
  • Manhã:
    1. arquivo com comandos da aula do dia anterior - revisão, alterar e expandir os comandos
    2. Mais simulações: arquivo 2 simulações do modelo geoestatístico básico no R, feitas de várias formas
    3. arquivo de comandos de uma análise incluindo inferência Bayesiana
  • Tarde:
    1. Modelos não gaussianos.
       1. arquivo 5 Simulação de modelos GLM geoestatísticos (Poisson e Binomial)
       2. Análises usando a geoRglm:
          • Análise com o modelo Poisson geoestatístico
          • arquivo com código para exemplo de simulação e análise de dados binários em 1-D
          • arquivo de dados binários para análise com geoRglm
    2. Representação de dados espaciais no R pelo pacote sp. SpatialPolygons e algumas visualizações e análises de dados de áreas
       1. Arquivo de comandos visto na aula
       2. Convertendo um objeto de áreas/polígonos em geodata (centroides como coordenadas)
          • arquivo de comandos
          • Arquivos shapefile bairros.shp bairros.shx bairros.dbf
          • Atributos dos bairros
       3. Montar geodata a partir da importação de dados de centroides de municípios do Paraná
          • shape com o estado do PR (arquivo dbf, arquivo shp, arquivo shx)
          • shape com os municípios do PR (arquivo dbf, arquivo shp, arquivo shx)
          • arquivo de atributos
          • Script de análise

• 09/10: Estudos de caso, extensões e outras análises (processos pontuais e áreas)
  • Manhã:
    • SKATER
    • Análise espacial de experimentos
    • Dados composicionais (frações de solo)
    • {http://www.ij-healthgeographics.com/content/10/1/17|Padrão espacial na resistência a antibióticos - EUREQA}
  • Tarde:
    • Abundância por classes de idade (pescada)
    • Zona de captura
    • Relação de variáveis de solo e ocorrência de espécies (Djair)
    • Processos pontuais (princípios e conceitos básicos)
• 10/10
  • Tarde:
    • Apresentação e discussão de análises, temas e projetos de participantes do curso
    • Modelo/código para Análise conjunta de diversas áreas

• "Slides" do curso

• 13/09
  • Manhã:
    • Instalar o R e depois instalar o pacote adicional geoR (install.packages("geoR", dep=T))
    • Fazer o download para um diretório (criar um) de trabalho do arquivo de dados e do arquivo de comandos
    • Rodar os comandos do arquivo, interpretar e discutir os resultados
    • Discussão dos passos da análise: estrutura e importação dos dados, gráficos exploratórios e sua interpretação
    • Pontos para atenção: dados atípicos (globais e locais), natureza da resposta e eventual necessidade de transformação, tendências no comportamento das variáveis.
  • Tarde:
    • Discussão dos passos da análise (cont).: variogramas (empíricos) e sua interpretação
    • Ajuste de modelos a variogramas
    • Interpolação espacial e visualização dos mapas
• 14/09
  • Manhã:
    • Estatística espacial: tipos "básicos" de problemas e estruturas de dados (dados de áreas, geoestatísticos e de processos pontuais). Semelhanças e diferenças. Estratégias para análise e modelagem.
    • Exemplos de dados e problemas "geoestatísticos", estratégias de modelagem.
  • Tarde:
    • Exemplos de dados e problemas "geoestatísticos", estratégias de modelagem. (cont)
    • Formalização e notação para modelagem geoestatística.
• Materiais
  • Apresentação da primeira semana de aula sobre tipos básicos de problemas de estatística espacial
  • Leitura de revisão: Cap 1 e 2 de Diggle & Ribeiro
  • Arquivos de comandos com exemplos de análises (examinar antes da próxima aula)
    1. arquivo de dados usado no script
       • Comandos vistos em aula para porosidade total
       • Outro arquivo de comandos para estes dados
    2. arquivo de dados de teores de elementos em camada 0-20acacio-artigo1.pdf
    3. dados de salinidade de água
    4. arquivo com teores de elementos químicos em amostras de solo
  • Sugestão de leitura Cap 3 de Diggle & Ribeiro

• 20/09
  • Manhã: Caracterização dos modelos geoestatísticos e funções de correlação
  • Tarde:
    • Relações entre funções de correlação e trajetória dos processos,
    • Variograma e função e correlação
    • Simulação de processos
      • Arquivo editado durante a aula
      • Arquivos utilizados em anos anteriores (revisar/rodar)
        • Um arquivo de comandos com exemplos introdutórios de simulação no R (modelos não espaciais)
        • arquivo 3
        • arquivo 2 simulações do modelo geoestatístico básico no R, feitas de várias formas
        • arquivo de comandos 1 Um breve tutorial de uso da função grf()
        • arquivo 5 Simulação de modelos GLM geoestatísticos (Poisson e Binomial)
        • Definir e montar um conjunto de simulações. Montar o seu arquivo de comandos.

• Arquivos editados nas aulas
  • Modelos para dados de precipitação no PR
  • Modelos para dados Ca20

• Tarefas
  • Refazer análises do arquivo usado na 1a semana da aulas em outro programa (outro pacote do R ou outro software)
  • Alunos estatística (compulsório) / outros cursos (opcional)
    • Escrever verossimilhança para estimar parâmetros com variâncias diferentes em diferentes áreas
    • Escrever verossimilhança o modelo básico com uma função de correlação de suporte compacto (alcance finito) utilizando algoritmos de matrizes esparsas para operar com a matriz de covariâncias (ver pacote sparseM)
    • Verossimilhança para distribuição t-multivariada
    • Verossimilhança composta (Naimara)

• 04/10
  • Manhã:
    • Anisotropia e estacionaridade - extensões do modelo
    • Predicões e simulações condicionais
    • Predicao de funcionais
    • arquivo de comandos básico do curso foi atualizado
  • Tarde
    • Discussão e temas variados
    • Aula interrompida devido à falta de energia elétrica

• 05/10
  • Manhã: Representação e dados espaciais
    1. Convertendo um objeto de áreas/polígonos em geodata (centroides como coordenadas)
       • arquivo de comandos
       • Arquivos shapefile bairros.shp bairros.shx bairros.dbf
       • Atributos dos bairros
    2. Montar geodata a partir da importação de dados de centroides de municípios do Paraná
       • shape com o estado do PR (arquivo dbf, arquivo shp, arquivo shx)
       • shape com os municípios do PR (arquivo dbf, arquivo shp, arquivo shx)
       • arquivo de atributos
       • Script de análise
  • Tarde:
    • Inferência e predição Bayesiana
    • arquivo de comandos básico do curso foi atualizado

• 04/10
  • Manhã:
    • Revisão GLM. Simulações do GLM/GLGM
      • arquivo de comandos de simulações
      • Simulação de modelos GLM geoestatísticos(Poisson e Binomial)
    • Análises usando a geoRglm:
      • Análise com o modelo Poisson geoestatístico
      • arquivo com código para exemplo de simulação e análise de dados binários em 1-D
      • arquivo de dados binários para análise com geoRglm

• 18/08
  • Manhã:
    • Apresentação e Introdução ao Sistema Estatístico R.
    • Motivação para geoestatística: interpolação, alternativas, algoritmos, modelos determinísticos e estocásticos
  • Tarde:
    • Exemplo da aula: um script com os passos básicos de uma análise geoestatística canônica
    • Discussão dos resultados do script. Passos da análise: (i) preparação dos dados, (ii) análise exploratória (distribuição, tendências, dados discrepantes globais e locais), (iii) modelos/inferência/estimação, (iv) predição (krigagem)
• 19/08
  • Manhã:
    1. Lendo e analisando dados (experimentar com os seus dados e/ou com os dados a seguir)
       1. arquivo de dados usado no script
          • Comandos vistos em aula para pororidade total
          • Outro arquivo de comandos para estes dados
       2. arquivo de dados de teores de elementos em camada 0-20
       3. dados de salinidade de água
       4. arquivo com teores de elementos quimicos em amostras de solo
    2. Passos da análise de dados: preparação, exploratória, modelagem/estimação, predição
  • Tarde:
    1. Lendo dados e análise geoestatística dados
    2. Tipos de dados espaciais: variação contínua (geoestatístico), discreta (areas) e processos pontuais
       • Exemplo de alguns comandos para análise de dados espaciais de direrentes tipos

Atividades:

1. Ler Capítulos 1 e 2 de Diggle e Ribeiro (2007)
2. Selecionar um artigo que utilize métodos geoestatísticos e preparar uma resenha
3. revisar, alterar e experimentar com os scripts vistos em aula
4. Montar geodata a partir da importação de dados de centroides de municípios do Paraná
   • shape com o estado do PR (arquivo dbf, arquivo shp, arquivo shx)
   • shape com os municípios do PR (arquivo dbf, arquivo shp, arquivo shx)
   • arquivo de atributos
   • Script de análise

• Script de análise

1. Convertendo um objeto de áreas/polígonos em geodata (centroides como coordenadas)
   • arquivo de comandos
   • Arquivos shapefile bairros.shp bairros.shx bairros.dbf
   • tabela de atributos tabe.csv

Atividades:

• Examinar a página de tutoriais da geoR. Rodar os seguintes tutoriais:

• 25/08
  • Manhã:
    • Montando geodata passo a passo (arquivo de comandos)
    • Problemas e alternativas de modelagem geoestatística
  • Tarde:
    • Análises de dados
    • Modelo geoestatístico básico e extensões
• 16/08
  • Manhã:
    • Características e elementos do modelo geoestatístico e funções de correlação
  • Tarde:
    • exemplos
    • Representação de objetos espaciais e fundamentos do pacote sp

• 15/09
  • Manhã:
    • Modelos geoestatísticos, características, estacionariedade, anisotropia, simulações
    • Variogramas teóricos e experimentais. Estimação por variograma dos parâmetros do modelo. Características e observações sobre o método de estimação
  • Tarde:
    • Praticando Simulação
      • Um arquivo de comandos com exemplos introdutórios de simulação no R (modelos não espaciais)
      • arquivo 3
      • arquivo 2 simulações do modelo geoestatístico básico no R, feitas de várias formas
      • arquivo de comandos 1 Um breve tutorial de uso da função grf()
      • arquivo 5 Simulação de modelos GLM geoestatísticos (Poisson e Binomial)
      • Definir e montar um conjunto de simulações. Montar o seu arquivo de comandos.
    • Métodos de estimação: máxima verossimilhança
• 16/09
  • Manhã:
    • Modelos geoestatísticos, simulações em alguns modelos estatísticso e geoestatísticos
    • Predição espacial e krigagem. Esperança, variância e simulações condicionais. Estimação de funcionais
  • Tarde:
    • Exemplo de código básico para predição espacial (arquivo de comandos), incluindo agora exportação dos resultados
    • Inferência e predição Bayesiana para modelos geoestatísticos Gaussianos
      • Ver e reproduzir os comandos abaixo da aula da Semana 3 de 2010 sobre predição, simulação condicional e análise Bayesiana

• 23/09
  • Manhã: Revisão GLM. Simulações do GLM/GLGM
    • arquivo de comandos de simulações
    • Simulação de modelos GLM geoestatísticos(Poisson e Binomial)
  • Tarde:
    • Análise com o modelo Poisson geoestatístico
    • arquivo com código para exemplo de simulação e análise de dados binários em 1-D
    • arquivo de dados binários para análise com geoRglm

• 20/10
  • Manhã e parte da tarde:
    1. Exemplo de alguns comandos para análise de dados
    2. Arquivo com análises de dados de área
    3. Alguns comandos para análises de processos pontuais
    4. análises de dados de áreas
    5. Arquivos usados nos scripts
  • tarde:
    1. fundamentos de análise de procesos pontuais
    2. apresentação alunos (ver material)
• 20/10
  • Manhã:
    1. fundamentos de análise de dados de áreas
    2. algumas aplicações de geoestatística: análise espacial de experimentos e ánalises conjuntas
  • tarde:
    1. interpolações não espaciais (arquivo de comandos com exemplos e alternativas)
    2. apresentação alunos (ver material)

• 16/09
  • Manhã:
    • Exemplo da aula
  • Tarde:
    • Arquivo de comandos
      1. arquivo de dados usado no script
• 17/09
  • Manhã:
    • arquivo de dados de teores de elementos em camada 0-20
    • dados de salinidade de água
    • arquivo de comandos editado na aula da tarde
  • Tarde
    • Análise de Fosforo mostrada na aula
      • arquivo com teores de elementos quimicos em amostras de solo

• 23/09
  • Scripts de simulação de Processos Gaussianos e de Dados geoestatísticos
    • simulações com animação
    • simulação de dados Gaussianos
    • Simulação de dados não Gaussianos (modelo linear generalizado geoestatístico
    • simulação do modelo bivariado
• 24/09
  • script modificado do dia 24/09 (atualizado, atualizar também a instalação da geoR)
  • Tarde : Exemplos de Importação de Dados(Ricardo Olinda)
    1. Tarefa 1 : montar geodata a partir da importação de dados de centroides de municípios do Paraná
       • Arquivos de dados:
       • shape com o estado do PR (arquivo dbf, arquivo shp, arquivo shx)
       • shape com os municípios do PR (arquivo dbf, arquivo shp, arquivo shx)
       • arquivo de atributos
       • Script de análise

• 14/10
  • Simulações condicionais e predição de funcionais

    require(geoR)
    ml <- likfit(s100, ini=c(1, 0.3))
    gr <- expand.grid(seq(0,1,len=50), seq(0,1, l=50))
    args(output.control)
    ## definindo simulacoes nos resultados (output)
    OC <- output.control(n.pred=1000, simulations.pred=T)
    kc <- krige.conv(s100, loc=gr, krige=krige.control(obj.m=ml), out=OC)
    ## vendo o que tem nos resultados 
    names(kc)
    str(kc)
    ## os simulacoes ficam armazenadas aqui
    dim(kc$simulations)
    ## calculando (predizendo) FUNCIONAIS
    ## FUNCIONAL 1: mapa de probabilidade do atributo estar acima de 1,8 
    p1.8 <- apply(kc$simulations, 1, function(x) mean(x>1.8))
    length(p1.8)
    image(kc, val=p1.8)
    ## adicionando legenda
    args(legend.krige)
    legend.krige(x.leg=c(1.05, 1.1), val=p1.8, y.leg=c(0.2, 0.8), vert=T)
    ## mudando os limites da image para incluir a legenda 
    image(kc, val=p1.8, xlim=c(0, 1.2))
    legend.krige(x.leg=c(1.05, 1.1), val=p1.8, y.leg=c(0.2, 0.8), vert=T)
    ## Outro funcional: proposção da área com valores acima de 1,8
    A1.8 <- apply(kc$simulations, 2, function(x) mean(x>1.8))
    length(A1.8)
    hist(A1.8, prob=T)
    lines(density(A1.8))
    rug(A1.8)
    summary(A1.8)
    ## outro funcional : distribuição dos máximos sobre a área
    MAX <- apply(kc$simulations, 2, function(x) max(x))
    length(MAX)
    hist(MAX, prob=T)
    lines(density(MAX))
    rug(MAX)
    ## probabilidade do MAX está acima de 4
    mean(MAX > 4)
    ## idem para minimo
    MIN <- apply(kc$simulations, 2, function(x) min(x))
    summary(MIN)
    hist(MIN, prob=T)
    lines(density(MIN))
    rug(MIN)
    ##
    ## um outro funcional diferente do anterior seria um mapa de maximos POR PIXEL
    MAX.map <- apply(kc$simulations, 1, function(x) max(x))
    length(MAX.map)
    image(kc, val=MAX.map)

• 15/10
  • Analise Bayesiana

    ## 
    require(geoR)
    sata(s100)
    args(krige.bayes)
    args(model.control)
    MC <- model.control()
    args(prior.control()
    ##
    ## definindo prior para beta e fixando os valores dos demais parâmetros
    ##
    PC <- prior.control(beta="flat", sigmasq.pr="fixed", 
                        sigmasq=1, phi.prior="fixed", phi=0.3)
    ## definindo grid de predição
    gr <- as.matrix(expand.grid(seq(0,1,len=50), seq(0,1,len=50)))
    ## obtendo posterioris e preditivas
    s100.kb <- krige.bayes(s100, loc=gr, model=MC, prior=PC)
    ## inspecionando o output
    names(s100.kb)
    names(s100.kb$posterior)
    ## vendo os resultados da posterioris
    s100.kb$posterior
    ## e as predicoes na preditiva...
    names(s100.kb$predict)
    s100.kb$predict$mean[1:10]
    s100.kb$predict$var[1:10]
    s100.kb$predict$dist
    image(s100.kb, col=terrain.colors(21))
    image(s100.kb, val=sqrt(s100.kb$predict$var), col=terrain.colors(21))
    ## mapa de um funcional: probabilidade de estar acima de 2.0
    ## calculando as probabilidades
    p2.0 <- pnorm(2.0, s100.kb$predictive$mean, sqrt(s100.kb$predictive$variance), low=F)
    ## e colocando no mapa
    image(s100.kb, val=p2.0, xlim=c(0, 1.2))
    args(legend.krige)
    legend.krige(x.leg=c(1.05, 1.15), y.leg=c(0.2, 0.8), p2.0, vert=T, off=0.3)
    image(s100.kb, val=p2.0, xlim=c(0, 1.2), col=terrain.colors(5))
    ##
    ## priori para beta e sigmasq
    ##
    args(prior.control)
    PCsig <- prior.control(beta="flat", sigmasq.pr="rec", phi.prior="fixed", phi=0.3)
    s100.kb.sig <- krige.bayes(s100, loc=gr, model=MC, prior=PCsig)
    names(s100.kb.sig)
    s100.kb.sig$posterior
    names(s100.kb.sig$predictive)
    ## pribalilidade na t (tem que corrigir o comando abaixo!!!!!
    p2.0 <- pt(2.0, s100.kb$predictive$mean, sqrt(s100.kb$predictive$variance), low=F) 
    s100.kb.sig$predictive$dist
    ##
    ## prioris em beta, sigmasq e phi
    ##
    args(prior.control)
    PCphi <- prior.control(beta="flat", sigmasq.pr="rec", phi.prior="rec", 
                           phi.disc=seq(0, 1.5, by=0.1))
    ## a chamada seria como abaixo (mas pode demorar muito para fazer predicao
    ## em um grid muito fino
    s100.kb.phi <- krige.bayes(s100, loc=gr, model=MC, prior=PCphi)
    ## definindo um grid mais "grosseiro" para teste
    gr <- as.matrix(expand.grid(seq(0,1,len=30), seq(0,1,len=30)))
    s100.kb.phi <- krige.bayes(s100, loc=gr, model=MC, prior=PCphi)
    names(s100.kb.names)
    names(s100.kb.phi)
    s100.kb.sig$posterior
    s100.kb.phi$posterior
    names(s100.kb.phi$posterior)
    s100.kb.phi$posterior$beta
    s100.kb.phi$posterior$sigmasq
    s100.kb.phi$posterior$phi
    names(s100.kb.phi$posterior)
    s100.kb.phi$posterior$sample
    ## visualizando as posterioris (marginais)
    ## beta|y
    hist(s100.kb.phi$posterior$sample[,1], prob=T)
    density(s100.kb.phi$posterior$sample[,1])
    lines(density(s100.kb.phi$posterior$sample[,1]))
    rug(s100.kb.phi$posterior$sample[,1])
    ## sigmasq|y
    hist(s100.kb.phi$posterior$sample[,2], prob=T, main=expression(sigma^2))
    lines(density(s100.kb.phi$posterior$sample[,2]))
    rug(s100.kb.phi$posterior$sample[,2])
    ## phi|y
    barplot(table(s100.kb.phi$posterior$sample[,3]))
    ## grafico "automatico" da geoiR com priori e posteriori
    plot(s100.kb.phi)
     
    ## experimentando com diferentes prioris
    ## note que aqui nao vamos fazer predição!!!
    PCphi <- prior.control(beta="flat", sigmasq.pr="rec", phi.prior="unif", 
                           phi.disc=seq(0, 1.5, by=0.05))
    s100.kb.phi <- krige.bayes(s100, model=MC, prior=PCphi)
    plot(s100.kb.phi)
     
    ##
    PCphi <- prior.control(beta="flat", sigmasq.pr="rec", phi.prior="squar", 
                           phi.disc=seq(0, 1.5, by=0.05))
    s100.kb.phi <- krige.bayes(s100, model=MC, prior=PCphi)
    plot(s100.kb.phi)
     
    ## priori com amis pontos na discretizacao
    PCphi <- prior.control(beta="flat", sigmasq.pr="rec", phi.prior="unif", 
                           phi.disc=seq(0, 1.5, by=0.05))
    s100.kb.phi <- krige.bayes(s100, model=MC, prior=PCphi)
    plot(s100.kb.phi)
     
    ## especificando uma priori particular do usuário
    args(dgamma)
    curve(dgamma(x, 2, sc=0.05), from=0, to=1.5)
    curve(dgamma(x, 2, sc=0.1), from=0, to=1.5)
    curve(dgamma(x, 2, sc=0.15), from=0, to=1.5)
    ## discretizando
    PRIORphi <- dgamma(seq(0, 1.5, by=0.05), 2, sc=0.15)
    ## .. e garantindo que soma 1 na discreta
    PRIORphi <- PRIORphi/sum(PRIORphi)
    PCphi <- prior.control(beta="flat", sigmasq.pr="rec", phi.prior=PRIORphi, 
                           phi.disc=seq(0, 1.5, by=0.05))
    s100.kb.phi <- krige.bayes(s100, model=MC, prior=PCphi)
    plot(s100.kb.phi)

• 28/10
  • Manhã:
    • Simulando do GLGM
  • Tarde:
    • Análise do GLGM (dados binários e Poisson)
• 29/10
  • Modelo Bivariado script da aula
  • Tutoriais geoR:
    • simulação de dados sob modelo bivariado
    • analise de dados

• 17/09
  • Manhã:
    • Arquivo de comandos
  • Tarde:
    • arquivo de dados de teores de elementos em camada 0-20
    • arquivo com teores de elementos quimicos em amostras de solo
    • dados de salinidade de água
    • arquivo de comandos editado na aula da tarde
• 18/08
  • Manhã:
    1. Efetuar análises com variáveis dos dados dos arquivos acima. Escolher alguns arquivos e variáveis procurando fazer análises adequadas.
    2. Depois de ter tentado efetuar as análises mencionadas acima, experimente reproduzir os comandos dos arquivos a seguir. Reflita sobre os comandos utilizados e discuta os resultados.
       • Arquivo de comandos (análise do fósforo (P) de profund020a.txt
       • Arquivo com comandos do R com análise geoestatística utilizados na aula

• 24/09
  • Manhã: Propriedades dos modelos geoestatísticos e funções de correlação
  • Tarde: Propriedades dos modelos e simulação de campos aleatórios Gaussianos
    1. comandos-simula.r
• 25/09
  • Manhã: Estimação de parâmetros: variogramas e verossimilhança
  • Tarde: Predição espacial (krigagem)

• 22/10
  • Manhã: prática e Explorando a predição espacial: simulação condicional e predição de funcionais genéricos.
    • arquivo de comandos: análise de ctc40
    • Dados:
      • regioes.dat
      • bordas das sub-áreas: regiao1.dat, regiao2.dat, regiao3.dat
  • Tarde: prática e Análise espacial de experimentos

• 23/10
  • Manhã: Inferência Bayesiana para modelos geoestatísticos
  • Tarde: Integração com ambientes de SIG e p pacote aRT

• 29/10
  • Manhã: Revisão de análise Bayesiana do modelo geoestatístico
    • dados de salinidade de água e o arquivo de comandos
  • Tarde: Modelos Multivariados e Modelos para dados composicionais
    • simulação de dados bivariados
    • estimação e predição de dados bivariados
    • pacote geoComp versao preliminar
    • arquivo com comandos para análise dos dados composicionais
• 30/10: Modelo Linear Generalizado Geoestatístico
  • arquivo com código para exemplo de simulação e análise de dados binários em 1-D
  • arquivo com código para exemplo de simulação e análise de dados de contagem (Poisson)

1. Aula 1 (01/09/2008):
   • Manhã: introdução a estatística espacial. Análise espacial, estatística espacial e geoestatística
   • Transparências do curso, Session 1 Apresentação da primeira semana
   • página com comandos ilustrando algumas funcionalidades de estatística espacial
   • Uma versão expandida dos exemplos no link anterior
   • tarde: tipos de problemas e estruturas de dados em geoestatística
     • Transparências do curso, Session 2
2. Aula 2 (02/09/2008): introdução à análise geoestatística de dados
   • Arquivo de dados usado na aula (manhã)
   • Arquivo de comandos (análise do fósforo (P) de profund020a.txt
   • Arquivo com comandos do R com análise geoestatística utilizados na aula (2007)

1. Aula 3 (08/09/2008)
   • Uma visão de geoestatística baseada em modelos tranparências do curso, Session 3
   • Dados camada 1
   • subregioes: área 1, área 2, área 3
   • borda de toda a área
   • arquivo de comandos
2. Aula 4 (09/09/2008)
   1. Manhã: propriedades do modelo geostatístico e extensões. Simulação de dados transparâncias do curso Session 4 & 5
      • Exemplo de simulação de dados
   2. Tarde:
      • extensões do modelo básico transparâncias do curso Session 5 (cont.)
      • Estimação: variogramas e verossimilhança. Cross-validação. Escolha de modelos e critérios. Estudos de caso. transparências do curso Session 6.

• Atividade: para próxima aula deve-se:
  1. entregar o artigo e a resenha sobre ele. pode ser impresso ou eletrônico
  2. é altamente desejável que já tenham o banco de dados com análises feitas. Não compulsória a entrega ainda mas será para próxima aula. Na próxima aula devem discutir qq dúvida referente aos dados comigo e colegas.

1. Aula 5 (29/09/2008): predição espacial - krigagem. Propriedades, algorítmos e exemplos
   • Transparências do curso, Session 7: Fundamentos da interpolação espacial (krigagem)
   • arquivo de comandos utilizado na aula
2. Aula 6 (30/09/2008)
   • Dados: regioes.dat Estendendo a predição espacial simulações condicionais e predição de funcionais genéricos. Predição Bayesiana e Análise espacial de experimentos
   • bordas das sub-áreas: regiao1.dat, regiao2.dat, regiao3.dat
   • arquivo de comandos: análise de ctc40
   • analise espacial de experimentos

1. Aula 7 (20/10/2008): GLGM
   • Transparências do curso, Session 9: GLGM
   • arquivo de comandos para simulação de GLGM
2. Aula 8 (20/10/2008): GLGM
   • Transparências do curso, Session 10: GLGM - estudos de caso
   1. Simular dados nas coordenadas as estações meteorológicas do Paraná (geoR: data(parana)) segundo o GLGM Poisson de média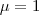 , , 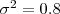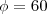e offset pelos dados no arquivo (mesma ordem das coordenadas das estações):
      • arquivo com valores de offset para simulação
   2. Analisar os o conjunto de dados simulados usando a geoRglm obtendo inferências sobre os parâmetros e predição da intensidade no estado
      • arquivo com comandos

1. Aula 9 (03/11/2008): GLGM e extensões do modelo geoestatístico
   • Transparências do curso, Session 9: GLGM - comentários adicionais sobre implementação do algorítimo MCMC na geoRglm
   • Estudos de caso, RAPLOA: Transparências do curso, Sessão 10
   • Extensões do GLGM: variogramas e processo pontual Log-Cox Gaussiano, Transparências do curso, Sessão 11
   • Processos pontuais marcados e amostragem preferencial, Transparências do curso, Sessão 11
     • artigo de Schlather, Ribeiro e Diggle sobre teste de independência entre marcas e pontos
     • artigo de Yongtao Guan sobre o mesmo tema
   • Delineamentos geoestatísticos, Transparências do curso, Sessão 11
     • artigo: Bayesian Geostatistical design
2. Simular processos pontuais: (a) Poisson homogêneo, (b) Poisson não homogêneo, © Log-Cox Gaussiano. No ultimo caso verificar o efeito dos parâmetros do modelo.
3. Simular processos pontuais marcados: (a) com marcas e pontos independentes, (b) marcas e pontos dependentes
4. Aula 10 (04/11/2008): Extensões do modelo geoestatístico
   • modelos espaço temporais - opções e abordagem utilizando funções de covariância espaço temporais. Um exemplo de aplicação
   • combinando geoestatística e análise de dados composicionais – um exemplo na avaliação de estoque de peixes
   • Modelos geoestatísticos multivariados. Construção de modelos, opções e o BGCCM
     • Um artigo com uma aplicação do BGCCM
   • Classes para dados espaciais no pacote sp
     • notas introdutórias
     • ver página do livro ASDAR

• dados de características de solo (arquivo de dados)
• precipitação no PR em 1993 (arquivo de dados)
• propriedades físicas do solo (arquivo de dados)
• porosidade e outras características do solo a 30 cm (arquivo de dados)
• Arquivo com comandos do R com análise geoestatística utilizados durante aula
• outro arquivo com comandos do R com análise geoestatística utilizados durante aula